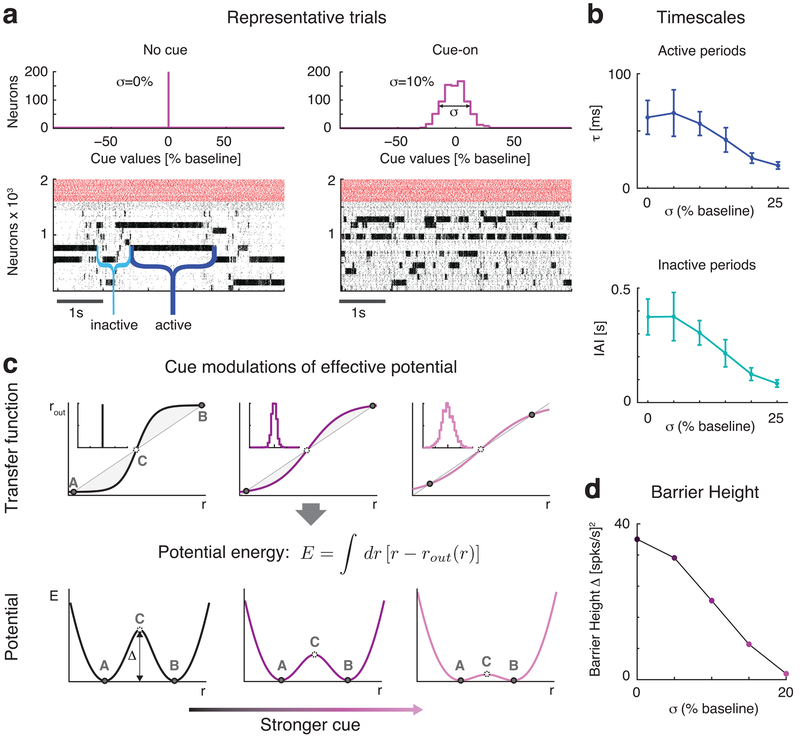
Fig. 3: Anticipatory cue speeds up network dynamics.
a: Raster plots of the clustered network activity in the absence (left) and in the presence of the anticipatory cue (right), with no stimulus presentation in either case. The dynamics of cluster activation and deactivation accelerated proportionally to the increase in afferent currents’ variance σ2 induced by the cue. Top panels: distribution of cue peak values across excitatory neurons: left, no cue; right, distribution with S.D. σ = 10% in units of baseline current. Bottom panels: raster plots of representative trials in each condition (black: excitatory neurons, arranged according to cluster membership; red: inhibitory neurons). b: The average cluster activation lifetime (top) and inter-activation interval (bottom) significantly decrease when increasing σ (mean±s.e.m. across n=20 simulated networks). c: Schematics of the effect of the anticipatory cue on network dynamics. Top row: the increase in the spatial variance of cue afferent currents (insets: left: no cue; stronger cues towards the right) flattens the “effective f-I curve” (sigmoidal curve) around the diagonal representing the identity line (straight line). The case for a simplified two-cluster network is depicted (see text). States A and B correspond to stable configurations with only one cluster active; state C corresponds to an unstable configuration with 2 clusters active. Bottom row: shape of the effective potential energy corresponding to the f-I curves shown in the top row. The effective potential energy is defined as the area between the identity line and the effective f-I curve (shaded areas in top row; see formula). The f-I curve flattening due to the anticipatory cue shrinks the height Δ of the effective energy barrier, making cluster transitions more likely and hence more frequent. d: Effect of the anticipatory cue (in units of the baseline current) on the height of the effective energy barrier Δ, calculated via mean field theory in a reduced two-cluster network of LIF neurons (see Methods).