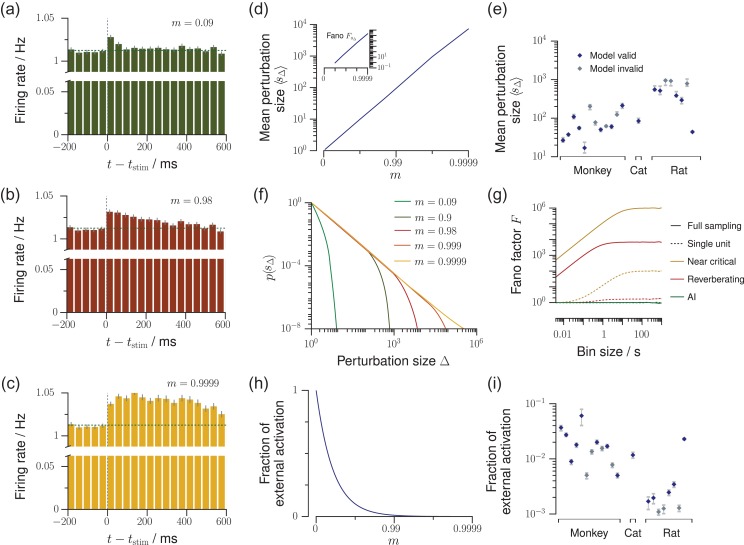
Figure 5.

Predictions about network dynamics and propagation of perturbations. Using our in vivo-like, reverberating model, we can predict several network properties, which are yet very complicated or impossible to obtain experimentally. (a–c) In response to one single extra spike, a perturbation propagates in the network depending on the branching ratio $m$, and can be observed as a small increase of the average firing rate of the sampled neurons, here simulated for 500 trials (as in London et al. 2010). This increase of firing rate decays exponentially, with the decay time $\tau$ being determined by $m$. The perturbation a is rapidly quenched in the asynchronous-irregular state, b decays slowly over hundreds of milliseconds in the reverberating state, or c persists almost infinitely in the critical state. (d) The average perturbation size $s_{\mathrm{\Delta }}$ and Fano factor $F_{s_{\mathrm{\Delta }}}$ (inset) increase strongly with $m$. (e) Average total perturbation sizes predicted for each spike recording of mammalian cortex (errorbars: 5–95% confidence intervals). (f) Distribution $p(s_{\mathrm{\Delta }})$ of total perturbation sizes $s_{\mathrm{\Delta }}$. The asynchronous-irregular models show approximately Poisson distributed, near-critical models power-law distributed perturbation sizes. (g) Bin size dependent Fano factors of the activity, here exemplarily shown for the asynchronous-irregular ($m\mathrm{=\; 0}$, green), representative reverberating ($m\mathrm{=\; 0.98}$, red), and near critical ($m\mathrm{=\; 0.9999}$, yellow) models. While the directly measurable Fano factor of single neurons (dotted lines) underestimates the Fano factor of the whole network, the model allows to predict the Fano factor of the whole network (solid lines). (h) The fraction of the externally generated spikes compared to all spikes in the network strongly decreases with larger $m$. (i) Fraction of the externally generated spikes predicted for each spike recording of mammalian cortex (errorbars as in e).