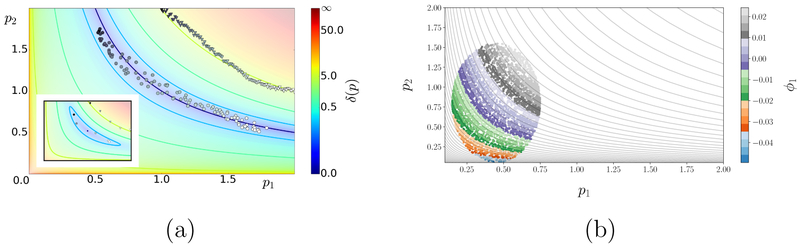
Figure 1:

Exact and learned (global) parameter space foliations for the model f_ε (p₁, p₂) = (p₁p₂ + 2ε(p₁ – p₂), ln(p₁p₂), (p₁p₂)²). The combination p_eff = p₁p₂ is an effective parameter for the unperturbed (ε = 0) model, since f₀ =const. whenever p₁p₂ =const. (a) Level sets of the cost function δ(p) = ∥f_ε (p) – f* ∥ for the unperturbed (main) and perturbed (inset) model and for data f* = (1, 0, 1) corresponding to (p₁, p₂) = (1,1). Level sets of p_eff can be learned by data fitting: feeding various initializations (triangles) to a gradient descent algorithm for the unperturbed problem yields, approximately, the hyperbola p_eff = 1 (circles; colored by initialization). This behavior persists qualitatively for ε = 0.2 despite the existence of a unique minimizer p*, because δ (p) remains within tolerance over extended almost neutral sets around p* that approximately trace the level sets of p_eff. (b) Learning p_eff by applying DMAPS, with an output-only-informed metric (see the SI), to input–output data of the unperturbed model. For ε = 0, points on any level curve of p_eff are indistinguishable for this metric, as f₀ maps them to the same output. DMAPS, applied to the depicted oval point cloud, recovers those level curves as level sets of the single leading nontrivial DMAPS eigenvector ϕ₁.