Time-lagged associations between cognitive and cortical development from childhood to early adulthood

Abstract

Throughout childhood and adolescence, humans experience marked changes in cortical structure and cognitive ability. Cortical thickness and surface area, in particular, have been associated with cognitive ability. Here we ask the question: What are the time-related associations between cognitive changes and cortical structure maturation. Identifying a developmental sequence requires multiple measurements of these variables from the same individuals across time. This allows capturing relations among the variables and, thus, finding whether: (a) developmental cognitive changes follow cortical structure maturation, (b) cortical structure maturation follows cognitive changes, or (c) both processes influence each other over time. 430 children and adolescents (age range = 6.01 – 22.28 years) completed the WASI battery and were MRI scanned at three time points separated by ≈ 2 years (mean age t1 = 10.60, SD = 3.58, mean age t2=12.63, SD=3.62, mean age t3=14.49, SD=3.55). Latent Change Score (LCS) models were applied to quantify age-related relationships among the variables of interest. Our results indicate that cortical and cognitive changes related to each other reciprocally. Specifically, the magnitude or rate of the change in each variable at any occasion –and not the previous level– was predictive of later changes. These results were replicated for brain regions selected according to the coordinates identified in the Basten et al.’s (2015) meta-analysis, to the Parieto-Frontal Integration Theory (P-FIT, Jung & Haier, 2007) and to the whole cortex. Potential implications regarding brain plasticity and cognitive enhancement are discussed.

1.1. Development of brain cortex and intellectual abilities

Understanding the biological bases of individual differences in cognitive abilities is a key goal of research in human intelligence (Deary, Penke, & Johnson, 2010; Haier, 2017). Studies of the development of cognitive abilities have consistently found a general increase from childhood to early adulthood. This process is characterized by rapid growth during early childhood and a progressive deceleration of this growth during adolescence with respect to the general factor of intelligence (g) (Hunt, 2011). At some point between 20 and 30 years of age –the precise moment depends on the individual and the considered cognitive ability (McArdle, Ferrer, Hamagami, & Woodcock, 2002)–, most abilities reach a peak and start a slow decrease –e.g., working memory capacity, processing speed, or reaction time– (Kail, 1991; Kail & Ferrer, 2007; Kail & Park, 1992; Kail & Salthouse, 1994; Salthouse, 2009), whereas other abilities stop changing or continue to increase at a slower rate –e.g., crystalized intelligence.(Cattell, 1987; Horn & Cattell, 1966, 1967; McArdle et al., 2002).

On the other hand, cortical development is generally characterized by a bilateral thinning in the four lobes. This thinning appears to be slower in childhood, accelerated during adolescence, and again decelerated in young adulthood (Zhou, Lebel, Treit, Evans, & Beaulieu, 2015). In general, the thinning process is associated with cortical surface flattening, loss of surface area, and gyral white matter expansion (Alemán-Gómez et al., 2013). Despite the general thinning trend at the group level, studies have found cortical thickening in some adolescent individuals (c.f., Román et al., 2018). In fact, previous research has shown that environmental factors such as maternal parenting style have a relevant effect in childhood and adolescent cortical development (Whittle et al., 2014, 2016).

Brain structure is associated with human cognitive functions, with literature indicating that that individual differences in cognitive abilities are related to individual differences in various measures of brain structure (Colom & Thompson, 2013). Considering these associations, locating links between the maturational development of both domains from childhood to early adulthood is relevant for understanding the neurological basis of individual differences in general cognitive abilities.

An increasing number of studies have been conducted to understand these developmental patterns by analyzing their relations in healthy individuals from childhood to early adulthood. For example, Karama et al. (2009) found positive associations between a general factor of cognitive ability and cortical thickness in multimodal association areas in a sample of ages 6–18. They interpreted this finding as evidence for a distributed model of intelligence. Burgaleta, Johnson, Waber, Colom & Karama (2014) studied a sample of ages 6–21 and found that individuals with IQ gains over time show no significant changes in their cortical thickness, whereas those without any IQ change, and particularly with IQ decrements, show cortical thinning. Koenis et al. (2015) observed relations between changes in brain network efficiency and changes in intellectual performance (ages 9 to 18). Specifically, increases in intellectual functioning were related with increases in global and local efficiency as measured by fractional anisotropy (especially in the frontal and temporal areas), and with decreases in local efficiency based on streamline count (frontal cingulate and occipital areas). Román et al. (2018) analyzed the relation between developmental changes in general cognitive ability and cortical thickness and cortical surface area changes in individuals from 6 to 21 years, finding that increases in intelligence were generally associated with increases in total cortical thickness and cortical surface area. Moreover, in agreement with previous evidence, they found greater cortical decrease and smaller intellectual increase in older individuals.

Findings from this literature suggest substantial relations between cortical and intellectual development, but the aforementioned studies explored the such relations using concurrent associations between cognitive and cortical changes. Wendelken et al.’s (2017) research is one exception, however. They analyzed lead-lag relations between structural and functional brain indices and reasoning ability within an age range of 6–22 years. Their findings indicate that structural connectivity between rostrolateral prefrontal cortex and the inferior parietal lobe predicts changes in reasoning ability. Their conclusion was that maturation of white matter enhances reasoning. Nevertheless, only data at two time points were considered and they applied a regression model in which only structural connectivity was allowed to predict changes in cognitive ability. They did not explore the opposite possibility, nor did they include reciprocal influences in the same statistical model.

In short, there is a lack of fine-grained information about how the relations between intellectual and cortical development work, and what are their time-lagged sequences. It is well stablished that changes co-occur, but it is unknown whether (a) the development of cognitive abilities is driven by cortical development, (b) the other way around, or (c) both influence each other reciprocally. Finding sound answers to this question requires (a) repeated measures (>2) of both cognitive ability and cortical indices, and (b) an analytical technique appropriate for capturing their time-lagged influences.

1.2. Latent change score models for neurocognitive development

LCS models (also called Latent Difference Score, Ferrer & McArdle, 2003, 2010; McArdle, 2001, 2009; McArdle & Hamagami, 2001) have been increasingly used in the last decades due to their flexibility for modeling longitudinal change in multivariate systems, including mean changes and time-sequential dynamic relations. Their key feature is that they focus on the change in the variables –instead of their level–, and they allow studying which elements of a system have an effect on that change. For this, the latent changes on each of the variables are specified at each repeated occasion. These latent changes are modeled as the difference in the latent scores of a variable y between a given occasion and the next (Δy). At each occasion, the latent level is a function of the initial unobserved level (y₀), plus the accumulation of changes up to that occasion (see McArdle, 2009, for further details. See also Ferrer & McArdle, 2010, for a detailed revision of LCS applications to different research domains).

Among other advantages, these models allow: a) isolating measurement errors –and other sources of non-relevant variance– from the true variance in the studied variables, b) detecting sequences of –i.e., lead-lag– effects within and between the different variables of interest, and c) formally describing developmental trajectories with very different shapes, including increasing, decreasing, decelerated and explosive phenomena.

LCS models have been applied to investigate the relations between intellectual and cortical development. Most studies on this topic have focused on the association between cognitive decline and brain changes during later age. For example, McArdle et al. (2004) used LCS for studying the relations between change in lateral ventricles size and memory decline in adults aged 30–80 years at baseline. They found that the decrease in lateral ventricular size was a leading indicator of memory declines. Raz et al. (2008) investigated the relation of fluid intelligence and brain volume in a sample of adults. However, associations in the rates of change were not perceptible. Lövdén et al. (2014) used two repeated measures of white matter microstructure and several cognitive abilities in a sample of adults aged 81–103 years. They found that alterations of white matter microstructure in the corticospinal tract were associated with decreases in perceptual speed. Studying elderly individuals, Ritchie et al. (2015) found that longitudinal changes in white matter microstructure (indexed by fractional anisotropy, FA) were coupled with changes in fluid intelligence, but not with processing speed or memory. Studying the same sample, Anblagan et al. (2018) focused on the relation between hippocampal structure and declines in cognitive ability. They found that better hippocampal mean diffusivity at age 73 predict less decline in verbal memory, working memory and processing speed three years later. Kievit et al. (2018) demonstrated how to use LCS for a) detecting correlated change in brain and behavior in the context of a training intervention in a lifespan study, and b) characterizing differences between boys and girls in cortical development during adolescence. Bender, Prindle, Brandmaier & Raz (2016) found that longitudinal improvements in associative memory were significantly associated with linear reductions in FA and increases in radial diffusivity, in a sample of healthy adults from 18 to 79 years.

We note that existing studies included two repeated measures of the cognitive and brain variables of interest (c.f., Anblagan et al., 2018; Kievit et al., 2018; Lövdén et al., 2014; Raz et al., 2008; Ritchie et al., 2015). Therefore, latent change could be estimated at one time point only (t₂-t₁). This allows computing latent correlations between brain and cognitive changes, but it does not allow estimating more complex lead-lag relations involving longer sequences. Similarly, available studies focused mainly on ages beyond 18 years. Much is still unknown about the lead-lag relations between brain and cognitive development during childhood and adolescence. The present study addresses this issue by analyzing cognitive ability and cortical thickness measured at three time points, in a sample of ages ranging from childhood to late adolescence, as detailed in the next section.

1.3. Cortical regions related to intelligence

The P-FIT model is currently an acknowledged frame of reference for organizing research efforts and results observed across neuroscience studies of intelligence (Dubois, Galdi, Paul, & Adolphs, 2018; Jung & Haier, 2007). This model underscores the relevance of several parietal and frontal brain regions when accounting for individual differences in intelligence, although temporal and occipital regions are also included within the P-FIT framework (Pineda-Pardo, Martínez, Román, & Colom, 2016).

Nevertheless, Basten, Hilger, & Fiebach (2015) noted the qualitative nature of the first version of the P-FIT model (Jung & Haier, 2007) and, therefore, conducted one meta-analysis from published structural and functional neuroimaging studies. Interestingly, they distinguished the task and the individual differences approaches that were combined by Jung & Haier. The latter approach is much more relevant for analyzing how intelligence differences relate to brain structural and functional differences: “the fact that a brain region is commonly activated (when solving a cognitive task) does not imply that individual differences in this activation are linked to individual differences in intelligence” (Basten et al., 2015). Although the meta-analytic results were generally consistent with the general P-FIT framework, they did not find any overlap between structural and functional correlates of intelligence differences. Thus, for instance, the parietal lobe was not identified in the meta-analysis of structural studies.

Previous literature (c.f., Haier, 2017) has pointed out that the conceptual approach in Basten et al.’s (2015) might be helpful for studying the neurological basis of intelligence. We hold that their meta-analysis implied one step further because their results are purely quantitative, in contrast to the rather qualitative approach in the P-FIT model. Because of this, here we focus on the regions identified by Basten et al. (2015). However, we replicate all our analysis using the P-FIT regions. We report the P-FIT results in a supplementary file, together with the results for the whole brain.

1.4. The present study

Using the same data considered in the current report, Román et al. (2018) analyzed the brain-intelligence relationships from childhood (6 years) to early adulthood (21 years). They found: (a) substantial increments in intelligence scores estimated at the latent level, (b) statistically significant correlations between cortical changes (thickness and surface area) and intelligence changes, (c) as individuals grow older, cortical and intelligence changes were smaller, and (d) individuals with higher intelligence scores showed cortical thickness preservation at early adolescence. Nevertheless, Román et al. analyzed the correlation between simultaneous changes only, and they acknowledged that their findings “cannot tell if intelligence modulates cortical changes or the other way around”. The present investigation aims to extend what it is already known by focusing on this very issue.

Therefore, we (a) characterize the trajectories and intra-individual change in cognitive ability, cortical thickness, and cortical surface area, and (b) investigate the relations between these variables, and particularly their lead-lagged associations. Because simultaneous change was studied in previous literature, the question addressed here is: Does the development in cortical thickness or cortical surface drive cognitive development? Does cognitive development drive brain development? Do both processes exert reciprocal influences, as they unfold over time?

2. METHOD

2.1. Participants

Data used in the preparation of this article were obtained from the Pediatric MRI Data Repository created by the NIH MRI Study of Normal Brain Development (Evans, 2006). This is a multi-site, longitudinal study of typically developing children, from ages newborn through young adulthood, conducted by the Brain Development Cooperative Group and supported by the National Institute of Child Health and Human Development, the National Institute on Drug Abuse, the National Institute of Mental Health, and the National Institute of Neurological Disorders and Stroke (Contract #s N01-HD02–3343, N01-MH9–0002, and N01-NS-9–2314, −2315, −2316, −2317, −2319 and −2320). A listing of the participating sites and a complete listing of the study investigators can be found at http://www.bic.mni.mcgill.ca/nihpd/info/participating_centers.html. Informed consent from parents and adult subjects and child assents were obtained for all subjects enrolled at the centers involved. The IRB approval number was A11-M99–00. The sample was selected to be representative of the U.S. population (2000 Census data) in the relevant demographic variables (Evans, 2006)

From the total sample, we included all the intelligence scores, and all the brain measures that passed a lenient quality control (QC). Two data points were removed due to problems in the estimation of the cortical measures. This led to a sample of 430 children (205 females, 47.7%; 184 males, 42.8%). Table 1 reports the sample size and descriptive statistics for each variable and time point.

Table 1.

Descriptive statistics (n, means, standard deviations and full information Pearson correlations) for the observed variables across the three waves.

	Cortical Thickness	Cortical Surface	Block design	Matrices	Simil.	Vocab.
n t1	304	304	430	430	430	430
Mean t1	.00	.00	.00	.00	.00	.00
SD t1	1.00	1.00	1.00	1.00	1.00	1.00
Cortical Thickness t1	1.00
Cortical Surface t1	.18	1.00
Block design t1	−.36	.06	1.00
Matrices t1	−.28	.07	.72	1.00
Similarities t1	−.32	.12	.72	.75	1.00
Vocabulary t1	−.42	.05	.78	.80	.86	1.00
n t2	313	313	363	363	363	363
Mean t2	−.20	.17	.56	.49	.52	.48
SD t2	1.06	1.01	.97	.63	.76	.81
Cortical Thickness t2	1.00
Cortical Surface t2	.25	1.00
Block design t2	−.39	.03	1.00
Matrices t2	−.37	.08	.69	1.00
Similarities t2	−.45	−.01	.71	.64	1.00
Vocabulary t2	−.48	−.02	.71	.67	.85	1.00
n t3	190	190	217	217	217	216
Mean t3	−.40	.14	.97	.75	.84	.87
SD t3	1.01	1.03	.85	.55	.62	.64
Cortical Thickness t3	1.00
Cortical Surface t3	.21	1.00
Block design t3	−.20	.06	1.00
Matrices t3	−.21	.03	.59	1.00
Similarities t3	−.40	−.03	.62	.48	1.00
Vocabulary t3	−.37	.01	.57	.51	.79	1.00

Note: Total n = 420. 47.7% females, 42.8% males. All the scores were standardized with the first occasion as the reference (mean = 0, sd = 1).

The age range across all waves was 6.01 – 22.28 years (mean age t1 = 10.60, SD = 3.58, mean age t2=12.63, SD=3.62, mean age t3=14.49, SD=3.55). The time interval between assessments was very consistent between participants, and between measures for each participant: for the first interval, mean = 2.01 years, sd = .51, 10^th quantile = 1.63, 90^th quantile = 2.37, for the second interval, mean = 2.01 years, sd = .39, 10^th quantile = 1.63, 90^th quantile = 2.37. Only participants without prior history of psychiatric disorders, neurological, or other medical illnesses with central nervous system implications were selected.

2.2. Measures and procedures

Intelligence.

Intelligence was assessed with The Wechsler Abbreviated Scale of Intelligence (WASI, Wechsler, 1999). The battery included the tests Vocabulary, Similarities, Matrix Reasoning, and Block Design. The same forms of all four tests were administered at the three time points considered. It is common to age-norm raw scores from intelligence tests so that the mean score is the same (e.g., 100) at any given age. However, in this study we were interested in changes in ability level over time. Therefore, the scores were not age-normed. Instead, we standardized the raw scores so they had mean = 0 and sd = 1 at the first measurement occasion. This implies that the mean score, as well as the individual scores, were expected to show level changes over time. Participants were tested on the day or within a few days of scanning.

MRI acquisition.

A high-resolution 3D T1-weighted Spoiled Gradient Recalled (SPGR) echo sequence was applied for 1.5 Tesla scanners for each participant at each visit, with 1 mm isotropic data acquired sagittally (whole head). Main parameters during MRI acquisition were: TR = 22–25 ms, TE = 10–11 ms. Excitation pulse = 30°, refocusing pulse = 180°. FOV = AP 256 mm, LR 160–180 mm. Matrix size = AP 256 mm, LR for 1 mm isotropic. Slice thickness of ~1.5 mm for GE scanners (with a limit of 124 slices) was allowed to guarantee whole head coverage. Previous studies with this sample found no effect of scanner site on image acquisition (Burgaleta et al., 2014; Ducharme et al., 2016; Román et al., 2018). Further information about quality control and scanner sites can be found in Ducharme et al. (2016).

Surface-Based Morphometry.

CIVET pipeline (version 1.1.12) (Ad-Dab’bagh et al., 2006; Kim et al., 2005; MacDonald, Kabani, Avis, & Evans, 2000) was employed for the processing of MRIs images. Cortical thickness measures (CT) and Cortical Surface Area (CSA) were computed following the next steps: (1) linear registration (12-parameter) to MNI-Talairach (ICBM152) space, (2) images corrected for radio-frequency non-uniformities and a brain mask computed, (3) tissue classification into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF), (4) generation of high-resolution hemispheric surfaces with 40,962 vertices each, (5) registration of surfaces to a high-resolution template, (6) cortical thickness is computed by evaluating the distance, in mm, between the original WM and GM surfaces transformed back to the native space of the original MR images, then interpolated onto the surface template, (7) vertex-based areas computed directly on the resampled surfaces and measure local variations of area/volume contraction and expansion relative to the vertex distribution on the surface template, (8) data were smoothed using a 20-mm kernel for CT and 40-mm kernel for CSA. More information regarding these steps can be found in Karama et al. (2009).

Brain measures.

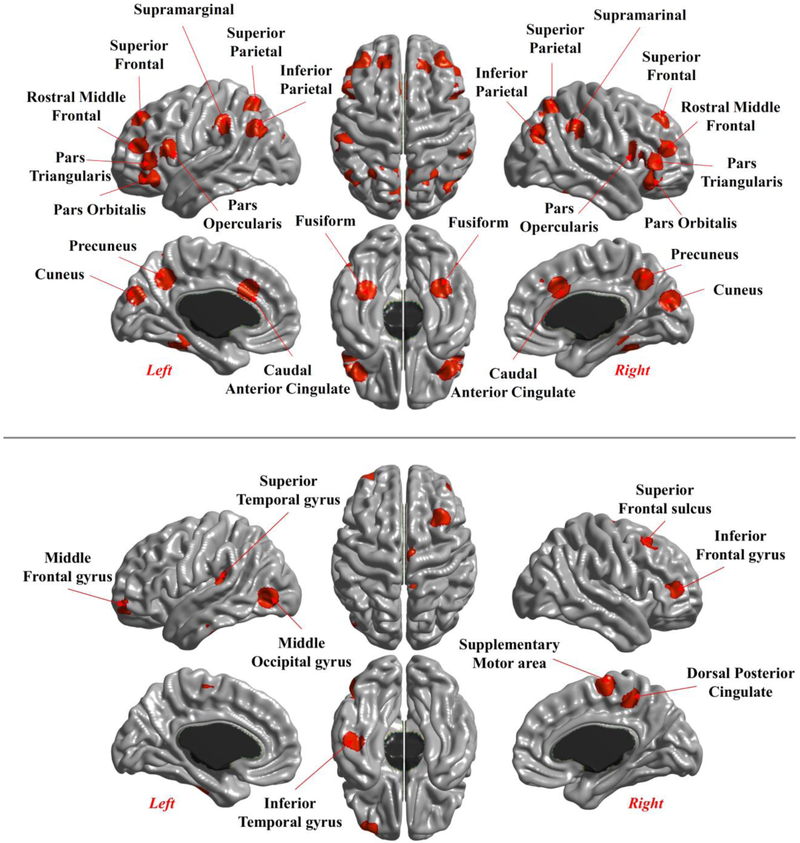
In this paper, we used the average cortical thickness (CT) and surface area (CSA) of a set of discrete regions of interest (ROIs) from the Basten et al. meta-analysis (Basten et al., 2015; see Figure 1, bottom panel). In the supplementary materials, we report the results from the same models regarding the ROIs in the P-FIT model (Jung & Haier, 2007; depicted in Figure 1, top panel), and for the whole brain. Average cortical thickness and total cortical surface area were estimated for each ROI using a size of 10mm (radius). We used the coordinates in Table 3 from Basten et al. (2015). For brevity, we refer to these composites as Cortical Thickness (CT) and Cortical Surface (CSA) We will report and compare the results for both types of brain measures.

Figure 1.

Regions of interest analyzed in our study, based on the P-FIT Theory (top) and the Meta-Analysis by Basten et al. (2015, bottom)

Note: The results for the P-FIT regions, and for the whole cortex, are presented in supplementary materials.

Table 3.

Nested model comparison

	g and Cortical Thickness (CT)							g and Cortical Surface Area (CSA)
	M1	M2	M3	M4	M5	M6		M1	M2	M3	M4	M5	M6
Num pars.	52	54	56	58	61	n.c.		52	54	56	58	61	n.c.
LogL	−3246	−3232	−3229	−3221	−3217			−3188	−3170	−3170	−3161	−3158
χ2	393.9	364.6	360.1	343.4	336.2			387.8	353.5	353.0	335.4	328.7
df	113	111	109	107	104			113	111	109	107	104
CFI	.954	.958	.959	.961	.962			.956	.961	.961	.963	.964
RMSEA	.076	.073	.073	.072	.072			.075	.071	.072	.070	.071
adj. BIC	6643	6619	6621	6610	6611			6526	6497	6502	6490	6492
Δ χ2		29.3	4.5	16.7	7.1				34.3	.5	17.6	6.7
Δ df		2	2	2	3				2	2	2	3
p		.000	.105	.000	.068				.000	.786	.000	.084

Note: n = 430. “n.c.” = Model did not converge. The selected model is shaded.

2.3. Analysis

We specified a common latent factor (g) representing general mental ability, measured by the four cognitive tests. Strong measurement invariance was imposed over the three measurement occasions (see Román et al., 2018, for details on the exact model specification).¹

In an LCS model, various specifications of the latent changes Δ_y are possible. In our study, we specified such changes are a function of: a) an additive linear component, adding the same amount each occasion², and captured by y_s, b) the latent levels at the previous occasion, both from the variable itself –i.e., self-feedback level to change, β_y–, and the other variable –coupling level to change, γ_y–, and c) the latent change during the previous interval, both from the variable –self-feedback change to change ϕ_y–, and the other variable –coupling change to change ξ_y. The latter change-to-change parameters are an interesting but infrequent extension of the classical LCS specification (Ferrer et al., 2007; Grimm, An, McArdle, Zonderman, & Resnick, 2012).

The latent intercept y₀, latent linear component y_s, self-feedback β and ϕ, and couplings γ and ξ capture different relevant features of the trajectory, and therefore they must be interpreted together. The means of the latent intercepts capture the mean levels in both processes at the first measurement occasion. The means of the latent slopes capture the average increase between two occasions in each variable for the whole sample. The variances of these latent components capture individual differences in initial levels and rates change. The covariances between these latent components capture the linear relations between them.

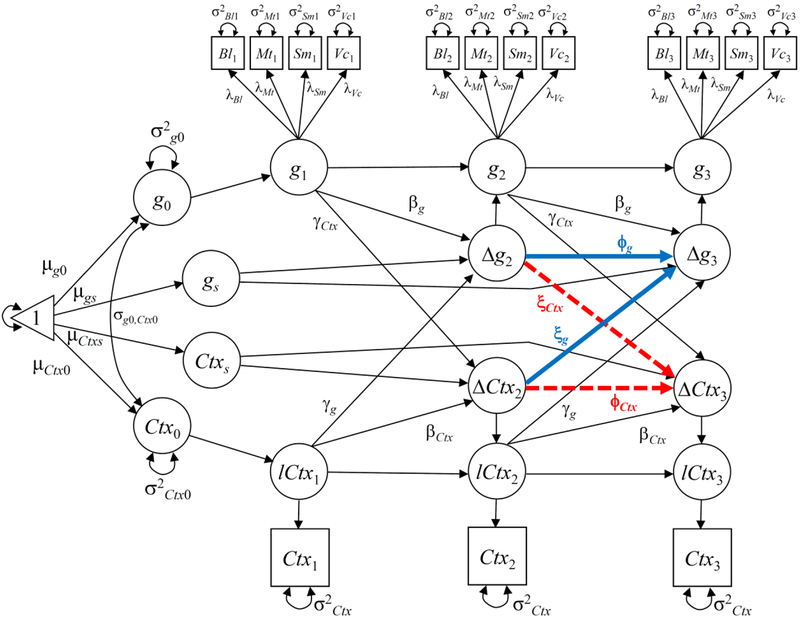
We conducted a separate set of analyses for CT and for CSA. We used the measurement occasion as the time signature. Therefore, the trajectories were composed of three time-points per case and variable. To account for the linear and non-linear effects of age on the variables, we included age and the natural logarithm of age at first occasion as predictors of the latent intercepts. In addition, age was rescaled based on the youngest value (5.94 years), so the minimum was zero in the new scale. Figure 2 depicts the LCS model for the two variables in each set of analyses.

Figure 2.

Path diagram of the Latent Change Score model (LCS, Model 4) for general cognitive ability (g) and Cortical Structure (Ctx, either Thickness or Surface) in the considered ROIs. Significant lead-lag effects are highlighted. The dashed line represents an effect for Cortical Thickness, but not for Cortical Surface Area.

Note: “Δ”=Change between previous and subsequent time point. “Bl”=Block Design. “Mt”=Matrices. “Sm”=Similarities. “Vc”=Vocabulary. All unlabeled parameters were fixed to 1. The two latent intercepts and two latent slopes are regressed on age and log(age) at first occasion (not shown). Intercepts of the four cognitive tests were estimated as time-invariant (not shown). Within-test residual auto-correlations (not shown) were allowed.

We examined the relations in the development of cortex (Ctx) and g through a set of nested model comparisons. First (Model 1), we fitted a bivariate LCS model in which the two variables were allowed to have residual variance in the latent intercept (i.e., differences at time 1 are not explained just by individual differences in age). These residual variances were allowed to covary. The variances and covariances for latent linear components, covariances between latent initial levels and linear components, as well as the self-feedback and coupling parameters were constrained to zero (σ_gs = σ_Ctx σ_gs-Ctxs = σ_g0-gs = σ_Ctx0-Ctxs = σ_g0-Ctxs = σ_gs-Ctx0 = γ_g = γ_Ctx = ϕ_g = ϕ_Ctx = ξ_g = ξ_Ctx = 0). Then, we compared this model with a set of less restricted versions of it (Models 2 to 6) in successive steps. Each comparison in the series allowed testing a specific hypothesis about the development of the two variables. Specifically, this procedure allows testing whether each additional freely estimated parameter contributes to increase the model fit –and, in consequence, to explain the observed trajectories (see Table 1 for details).

Models were compared through likelihood ratio tests (p values lower than α=.05 were considered statistically significant), as well as inspection of the fit indices: model log likelihood, RMSEA (Steiger & Lind, 1980), CFI (Bentler, 1990), and Sample-Size Adjusted BIC (Schwarz, 1978; Sclove, 1987). The differences between the models compared are detailed in Table 2.

Table 2.

Description of the Bivariate Latent Change Score models compared

Model 1 Age predicts latent intercept and slope - Residual variance estimated for latent intercept of g (σ2g0) and Ctx (σ2Ctx0) - Covariance between latent intercepts (σg0-Ctx0) - Self-feedback parameters from level (t-1) to changes (t) β g→Δg β Ctx→ΔCtx

Model 2 - Self-feedback from previous changes (t-1) to subsequent changes (t) ϕ Δg→Δg ϕ ΔCtx→ΔCtx

Model 3 - Couplings from level (t-1) to changes (t) γ g→ΔCtx γ Ctx→Δg

Model 4 - Couplings from previous changes (t-1) to subsequent changes (t) ξ Δg→ΔCtx ξ ΔCtx→Δg

Model 5 - Residual variance estimated for latent slope of g (σ2gs) and Ctx (σ2Ctxs) - Covariance between latent slopes (σgs-Ctxs)

Model 6 - Covariances between latent slopes and intercepts: σg0-gs, σCtx0-Ctxs, σg0-Ctxs, σCtx0-gs

Note: All the parameters estimated in a model are also estimated in subsequent models

All SEM analyses were carried out using Mplus 7.4 (Muthén & Muthén, 1998) with Full Information Maximum Likelihood estimation (FIML). The results were analyzed with the package MplusAutomation for R (Hallquist & Wiley, 2018). The Mplus code for all the models can be downloaded from https://github.com/EduardoEstradaRs/DevPsych2019-LCS-cortical-cognitive-development

3. RESULTS

3.1. Descriptive statistics

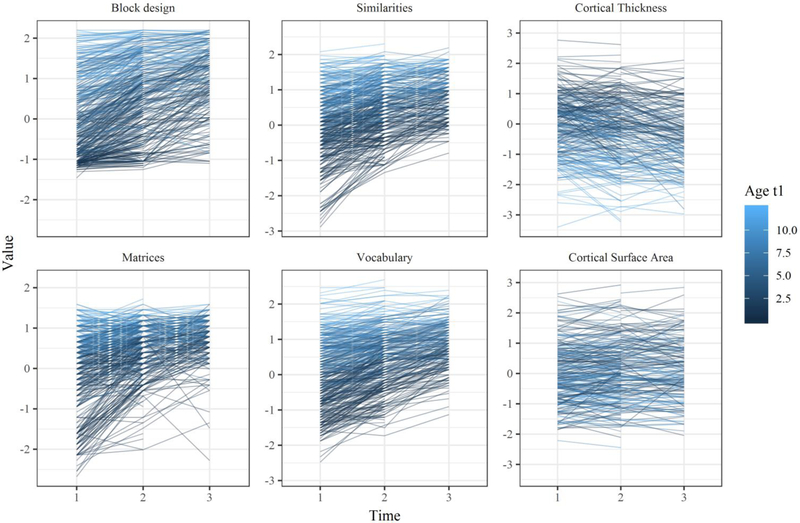
Table 1 shows the descriptive statistics and sample size for the variables at each occasion. Figure 3 depicts the individual trajectories in the observed variables. Table 1 and Figure 3 show that performance on the four cognitive tests increased from time 1 to time 3 for almost all individuals –as expected for the age range considered. CT and CSA show a decreasing trend for most, but not all, individuals.

Figure 3.

Individual trajectories for cortical thickness and the four cognitive tests across measurement occasions.

Note: Scores rescaled so they have mean=0 and sd=1 at time 1.

Considering CT, 29 cases experienced thickening from t1 to t3 (20.9% of 139 cases with both time points, mean Age₁ = 11.02 years, sd_Age1=4.3), whereas 110 cases experienced thinning (79.1%, mean Age₁ = 11.65 years, sd_Age1=3.27). Considering CSA, 68 cases experienced an increase (48.9%, mean Age₁ = 10.61 years, sd_Age1=3.56) and 71 cases experienced decrease (51.1%, mean Age₁ = 12.4 years, sd_Age1=3.24). Cortical thinning was not associated with younger ages at first occasion: Pearson correlation of r = −.07 (p=.431). In contrast, surface change was negatively associated with younger ages: r = −.28 (p<.001, i.e., older age was weakly associated with surface decrease). In any case, these correlations were very close to zero, and both increases and decreases were observed in individuals across the whole age range.

As expected, cognitive scores were positively correlated (zero-order r values ranging between .48 and .86, with a mean of .69). The two brain measures were positively –although weakly– correlated (r =.18 for t1, r=.25 for t2, and r=.21 for t3). The bivariate correlations between thickness and cognitive performance were negative and moderate (max r = −.20, min r = −.48, mean r = −.35), whereas the correlations between surface and cognitive performance were very close to zero (max r = .12, min r = −.03, mean r = .04).

3.2. Comparison of models for change

Table 3 shows the results from the model comparison. These models are nested, and, therefore, their fit difference can be tested. A separate set of analyses was conducted for the relation between g and CT, and for the relation between g and CSA. Despite the fact that Model 1 achieves good fit, the increase achieved by Model 2 is significant (χ²₍₂₎ > 29, p<.001, both for the CT and CSA). Indeed, all the fit indices consistently supported Model 2 over Model 1 for both datasets. This result entails that the changes observed during the interval t2–t3 are a function of the level achieved at the beginning of the interval, but such changes are better predicted when we take into consideration the changes in the same variable during the previous interval t2–t3 (ϕΔg→Δg and ϕΔCtx→ΔCtx).

Allowing non-zero level-to-change couplings (γCtx→Δg and γg→ΔCtx) in Model 3 did not lead to an increase in model fit. However, when we allowed the changes in each variable to be predicted by the changes in the other variable (i.e., change-to-change couplings ξΔCtx→Δg and ξΔg→ΔCtx) in Model 4, we observed a significant increase in model fit (p<.001 for both CT and CSA), with all fit indices supporting Model 4 over Models 3 and 2 in both datasets. These results strongly suggest that change in the variables is not predicted by the previous levels attained in the other variable, but by the change observed during the previous interval.

Allowing non-zero residual variances in the latent linear components of change, and a covariance between these residuals (Model 5), lead to a non-significant increase in model fit (p=.068 for CT, p=.084 for CSA). Model 6, which allowed non-zero covariances between latent intercepts and linear components, did not converge. In general, when a SEM model does not converge, it is not possible to draw inferences about the parameters in such model. However, non-converge is informative in the context of our nested model comparison. Model 6 did not converge, but the exact same model did converge when the covariances between the latent slopes and intercepts were constraint to zero (Model 5). Therefore, it is reasonable to think that the non-convergence was due to the fact that the common pattern of variance in the trajectories of g and Ctx was fully explained by the lead-lag loadings. Because there was no more covariance left to be explained, the estimation algorithm did not find a minimum in the fit function for Model 6. In other words, this result may indicate that there is not enough information in the empirical variance-covariance matrix for estimating the additional covariances in Model 6.

For both datasets, the Chi square test for nested model comparison showed that the additional parameters in Model 5 did not lead to a better fit than Model 4. Furthermore, RMSEA and aBIC were slightly better for Model 4, whereas CFI was only marginally better for Model 5. Overall, results shown in Table 3 suggest that Model 4 better characterized the development in our sample. Therefore, we selected Model 4 for parameter interpretation. These results provide support for the idea that a) the development of cognitive ability is related with the development of both CT and CSA, b) lead-lag influences are relevant for this development processes, and c) recent changes are relevant for predicting subsequent changes. The results for the regions from the P-FIT model, and for the whole brain, were fairly consistent, and can be found in the supplemental materials.

3.3. Developmental associations between cognition and cortical thickness

Table 4 shows the parameter estimates from the selected model (M4) for both data sets. Similarities and Vocabulary were the tests with highest contributions to the general factor (mean standardized loadings λ_Sim=.893 and λ_Voc=.925, both p<.001 in all occasions). This suggests that g had an important verbal component in our data. We found a linear effect of age on the latent intercepts of both general ability (g₀) and cortical structure (Ctx₀). The effect was positive for g (standardized δ = .572 for the CT and .582 for CSA) and negative for Ctx (std. δ = −.694 for CT and −.260 for CSA; all p ≤ .05). Age also had a positive nonlinear effect on g₀ (std. δ = .370 and .360, p < .001), and on CSA₀ (std. δ = .264, p = .031).

Table 4.

Parameter estimates of LCS Model 4

		Ctx = Cortical Thickness					Ctx = Cortical Surface Area
Parameter		Estimate	SE	p	Stzd. factor loading / Correlation		Estimate	SE	p	Stzd. factor loading / Correlation
Factor	λ Block Designc	1.000	fixed		.781b		1.000	fixed		.783b
loadingsa	λ Matricesb	.685	.042	.000	.713b		.685	.042	.000	.715b
(g measured by)	λ Similarities	.945	.028	.000	.892b		.945	.028	.000	.893b
	λ Vocabulary	1.014	.028	.000	.924b		1.014	.028	.000	.925b
Intercepts	τ g0	.000	fixed				.000	fixed
	τ gs	.742	.029	.000			.752	.026	.000
	τ Ctx0	.759	.078	.000			.138	.092	.132
	τ CtxS	−.052	.078	.505			.209	.046	.000
Regressions	δ Age → g0	.145	.013	.000	.572		.147	.013	.000	.582
	δ ln(Age) → g0	.304	.041	.000	.370		.296	.041	.000	.360
	δ Age → Ctx0	−.170	.027	.000	−.694		−.072	.032	.026	−.260
	δ ln(Age) → Ctx0	.084	.093	.367	.106		.238	.110	.031	.264
	δ Age → gs	−.057	.009	.000	−.938		−.062	.010	.000	−1.060
	δ ln(Age) → gs	−.014	.023	.554	−.069		.013	.027	.625	.068
	δ Age → CtxS	.028	.025	.262	1.230		−.003	.010	.787	−.083
	δ ln(Age) → Ctxs	−.143	.068	.034	−1.916		−.100	.045	.025	−.926
Determinants	β g → Δg	.051	.033	.129			.037	.039	.352
of change in g	ϕ Δg → Δg	−.208	.065	.001			−.526	.130	.000
	γ Ctx → Δg	.003	.017	.836			.014	.013	.293
	ξ ΔCtx → Δg	.330	.119	.005			1.016	.471	.031
Determinants	β Ctx → ΔCtx	.000	.047	.997			−.014	.014	.334
of change in Ctx	ϕ ΔCtx → ΔCtx	−.880	.221	.000			−.260	.586	.658
	γ g → ΔCtx	−.127	.094	.173			.014	.043	.741
	ξ Δg → ΔCtx	−.331	.139	.017			−.199	.154	.197
Latent residual	σ g0-Ctx0	.044	.018	.015	.173		.075	.022	.001	.211
variances-covar.	σ2 g0	.131	.013	.000	.160		.131	.014	.000	.160
	σ2 Ctx0	.490	.051	.000	.638		.971	.077	.000	.985

Note: n=430. Statistically significant parameters of interest are shaded (α=.05).

^“a”= factor loadings invariant across occasions (except for Matrices).

^“b”= mean across the three waves.

^“c”= parameter fixed.

“ln(Age)” = Natural logarithm of age, capturing non-linear influences. Intercepts for the observed indicators and residual variances are not shown. Standardized values for the intercepts and dynamic parameters are not interpretable, and therefore not shown.

Thus, on average, older individuals had higher levels of g, although the same age difference led to larger differences in ability at younger ages (i.e., the effect was nonlinear and decelerated). In contrast, older cases generally showed thinner cortices. The average cortical surface area remained fairly similar across the whole age range. We also found a linear effect of age on the latent rates of linear change of g. Older individuals experienced less increase in g (std. δ = −.938 and −1.060 for the CT and CSA models, respectively). The age had large negative nonlinear effects on the rates of linear change of cortical structure (std. δ = −1.916 for CT and −.926 for CSA).

One of the main goals of the present study was to investigate the time-lagged influences between cognitive ability and cortical structure. Thus, the dynamic parameters of the model –i.e., the lead-lag effects or determinants of change: self-feedback (β and ϕ) and couplings (γ and ξ)– are of great interest. The self-feedback effects capture the influence of the variables in their own later change. We found no significant level-to-change self-feedback (β), neither for g nor for Ctx. However, the change-to-change self-feedback (ϕ) was statistically significant in all cases (p ≤ .002), except for CSA (p = .658).

Couplings capture the influence of each variable on the change of the other variable in the system. We found no significant level-to-change coupling (γ). However, we did find a change-to-change coupling from the cortical measures to g (ξΔCtx→Δg, p < .05 both for CT and CSA): changes in cognitive ability were predicted by previous changes in both thickness and surface. Similarly, thickness changes were also predicted by previous changes in g (ξΔg→ΔCT). In contrast, surface changes were not predicted by previous changes in g (ξΔg→ΔCSA, p = .197).

In summary, the dynamic parameters shown in Table 4 support the next conclusions (Figure 2 offers a summary of the significant lead-lag effects in the model):

1. Change in cognitive ability is not predicted by previous level in either g, CT or CSA.

2. Change in cortical structure is not predicted by previous level in g, CT or CSA.

3. Change in cognitive ability is predicted by previous change in CT and CSA. Both cortical measures have positive effects: individuals who experienced less thinning and less surface loss during the previous interval showed more subsequent increase in g.

4. Importantly, change in thickness is negatively predicted by previous change in g: individuals who increased more in g during the previous interval showed greater subsequent thinning.

5. However, change in cortical surface is not predicted by previous change in either itself or g –i.e., change in CSA is not predicted by previous levels or rates of change in the system.

6. The significant self-effects of the change in g and CT on their own later change were negative: individuals who increased more in g during the previous interval showed less subsequent increase in g, and individuals who experience greater thinning during the previous interval showed smaller subsequent thinning.

The residual variance was significantly different from zero for the two latent intercepts (σ²_g0 and σ²_Ctx0). This entails that, after controlling the effect of age, individual differences were found in the initial levels of g and Ctx. The residual covariance between initial levels (σ_g0-Ctx0) was also significant, although moderate (.173 for CT and .211 for CSA, p<.05). The results for the regions from the P-FIT model, and for the whole brain, were totally consistent with the results reported here, and can be found in the supplemental materials.

4. DISCUSSION

4.1. Summary of findings

We sought to investigate the time-related associations between developmental cognitive changes (intelligence) and brain structural changes from childhood to early adulthood. We focused on average cortical thickness and surface area from a set of regions previously related with intelligence differences (Basten et al., 2015). Our primary goal was to investigate lead-lag effects between cognitive and biological developmental changes, as both processes unfold over time.

The key finding in our analysis is that cognitive ability and cortical thickness are mutually related over time. In particular, changes (and not current levels) in cognitive ability and cortical thickness in the considered regions predict subsequent changes in both variables. Although our models included level-to-change and change-to-change associations, only the latter appear to be relevant. In contrast, changes in cortical surface area predict changes in cognition, but are not predicted by the previous levels or rates of change in any variable. These lead-lag effects were found in a statistical model designed to capture effects of age as well as linear and nonlinear trends in the two variables of interest.

Interestingly, the increase in cognitive ability between the first and second measurement occasions was negatively related to changes in cortical thinning between the second and third measurement occasions –i.e., the effect cognition→thickness was negative. In contrast, the effects from thickness and surface to cognition were positive: individuals who experienced less thinning and surface loss showed more subsequent increase in cognitive abilities.

We also found significant and negative change-to-change self-feedback effects within cognitive abilities and thickness: larger cognitive ability gains between the first and second occasions were a significant predictor of modest ability gains from the second to the third occassions, and greater thinning predicted smaller subsequent thinning.

4.2. Theoretical and methodological considerations

Biological maturation, as measured by age, is linked to changes in cortical structure and cognitive ability. Previous research has shown how both of them develop as individuals transition from childhood to adulthood (Alemán-Gómez et al., 2013; McArdle et al., 2002; Zhou et al., 2015). However, as described in our study, a significant part of the variance in the changes in cognition and cortical thickness appears to be explained by the previous changes experienced by the individuals.

Regarding the effects from cognition to brain, it is unclear why the changes in cognitive ability appear to predict subsequent changes in cortical thickness, but not in cortical surface area. These results may be partly explained by the fact that cortical surface area shows smaller –in fact, arguable– changes during the age range considered here. As discussed by Zhou et al. (2015) there is substantial inconsistency in the published reports regarding cortical surface area changes across development. Thus, for instance, Wierenga et al. (2014), and Schnack et al. (2015) reported surface area increases before age 10 years, 11 years, and by 15 years, respectively. In those reports, surface area decreases afterwards. However, Alemán-Gómez et al. (2013) and Burgaleta et al. (2014) observed decreases in surface area within the 11–17 year range, or no change in surface area within the 6–20 year range, respectively. In clear contrast, cortical thinning is consistently found across the age range 7–22.

Understanding individual differences in human cognition, and how such differences emerge over the life span, requires approaches that a) characterize the normative trajectories of cognitive and neural phenotypes and help to understand how these processes unfold in development, and b) investigate how genetics and experience affect the timing and shape of these curves. This knowledge may inform our conceptual models and provide clinically applicable insights into what factors drive human development (c.f., Rosenberg, Casey, & Holmes, 2018). The present study is a step in that direction.

Our results suggest that the trajectories of both variables (cognitive and cortical) were adequately characterized by a bivariate LCS model. Change in these variables can be described as a function of: a) a linear additive rate of change, b) self-feedback effects, and c) coupling effects between general intelligence and cortical thickness.

The estimates from this model characterize a bivariate dynamic system that behaves very differently depending on its initial state. In other words, depending on the initial level of the two variables, the same parameters can lead to linear, nonlinear, increasing, decreasing or mixed tendencies for each of them. Because age is a predictor of the initial state, the model has considerable flexibility to capture different trajectories at different ages through its dynamic parameters. Furthermore, the linear and nonlinear effects of age on the additive components were able to pick up changes in the trajectories that were not captured by the dynamic parameters –including moderating effects of age. Interestingly, the couplings and self-feedbacks are significant in the presence of these complex age effects. This is consistent with the conclusion that the lead-lag associations detected are independent of age (within the range considered here).

Previous research has explored the influence of previous rates of change on subsequent changes. Indeed, the directionality ‘brain to cognition’ found here is consistent with studies conducted with elderly individuals. For example, Jack et al. (2005) found that cognitive impairments associated with Alzheimer disease were partially explained by the previous rate (together with the previous level) of ventricle atrophy. However, our finding that cognitive changes predict cortical changes (‘cognition → brain’) is entirely novel and suggests that the interrelations of brain and cognitive development may follow different sequences in childhood and adolescence, compared to older ages. In other words, the relations between cortical and cognitive development may differ substantially at different moments across the human lifespan.

From a methodological perspective, the present research is one of the few investigating lead-lag effects from previous changes to later changes, even in the context of LCS models. Ferrer et al. (2007) included these effects in their study of the developmental sequences between cognitive abilities and reading. Grimm et al. (2012) demonstrated how they can be specified in the context of LCS models. However, to the best of our knowledge, the present research is the first to incorporate these effects for investigating the relations between cognitive and cortical development.

Previous studies (cf., Wendelken et al., 2017) did not analyze simultaneous effects of reasoning on cortical change –i.e., changes in reasoning were the only variable considered as “dependent” in their linear regression model. The present study is the first investigation of reciprocal lead-lag effects between cognitive ability and brain structural differences. The finding that the previous rate of change –and not the previous level achieved– predicts subsequent changes is a novel contribution to the developmental literature. These results underscore the importance of including both cortical and cognitive changes as part of the same dynamic system, in order to identify the relevant effects in the presence of all the other effects within the system.

Considering only two of the three measurement occasions analyzed here, Burgaleta et al. (2014) found that gains in Full Scale IQ were negatively associated with cortical thinning: the larger the IQ gain, the greater the thickness preservation. The present work differs from Burgaleta et al.’s (2014) in the following points: a) we considered three waves of data, instead of two, which allows a more reliable measure of change (Willett, 1989); b) we went beyond a correlational approach and investigated time-lagged associations in the presence of a system of reciprocal influences; and c) we estimated our variables as latent factors, which allows separating the true variance in the latent construct from the variance due to measurement error –included in the IQ estimate. Because our model included lead-lag effects (from brain structure to cognition and vice-versa), instead of mere correlations, we were able to find a positive effect indicating that less thinning was predictive of larger subsequent intelligence gains (consistent with Burgaleta et al.’s, 2014), but a negative effect showing that larger intelligence gains predicted greater subsequent thinning.

4.3. Possible implications for brain plasticity and cognitive enhancement

The finding that intellectual changes and cortical changes reciprocally predict each other could have implications for attempts aimed at enhancing cognitive ability. As underscored by Haier (2017) “the ultimate purpose of all intelligence research is to enhance intelligence”. There is now a growing discussion regarding efficient ways for achieving this goal (Au et al., 2015; Au, Buschkuehl, Duncan, & Jaeggi, 2016; Colom & Román, 2018; Melby-Lervåg & Hulme, 2016), or even questioning if this is possible at all (Sala, Tatlidil, & Gobet, 2018; Simons et al., 2016).

It has been suggested that individuals with higher intelligence scores are systematically more engaged in intellectually demanding activities, and this contributes to keep brain integrity (Flynn, 2016). For instance, studying the 1936 Lothian Birth Cohort, Karama et al. (2014) found that childhood IQ (measured at age 11 years) explains more than two-third of the relation between the IQ assessed at age 70 and cortical thickness at age 73. These researchers discuss three alternatives for explaining the finding: (a) genes associated with intelligence in childhood are the same genes associated with intelligence in old age, (b) individuals with higher intelligence scores are systematically more engaged in intellectually demanding activities and this contributes to keep brain integrity, and (c) reciprocal dynamic associations between cortical thickness and intelligence. The second and third alternatives are consistent with our finding that changes in cognitive abilities predict subsequent cortical changes. In our sample, children and adolescents involved in more cognitively demanding activities may have accelerated their natural process of cognitive development and achieved a higher rate of change. In turn, this fastest rate of change may have led to changes in the regions of the cortex expected to be related with intelligence according to the brain regions highlighted by Basten et al. (2015).

In the same vein, Protzko (2015) conducted a meta-analysis on the fadeout effects systematically observed after the cessation of intelligence enhancement programs. He concluded that this fadeout effect is an inevitable consequence of the return to an impoverished environment. In light of our results, we suggest that the fadeout effect may be due to the inability of the enhancement programs to evoke and preserve actual changes in the individual’s cortices. Such morphological changes may be achieved only when the intellectual enhancement is fast enough –i.e., the amount of improvement during a given period of time is sufficiently large– to trigger reorganization in the cortex. It must be noted that this hypothesis is based solely on the correlational –although longitudinal– data of our research. Stronger evidence can be provided only by experimental studies applying programs that cause different rates of enhancement in different groups, and then comparing subsequent rates of cortical change between such groups.

4.4. Limitations and future directions

Despite the relevance of the results reported here, our models were unable to account for some of our findings. Namely, we found individual differences in the direction of the longitudinal change: contrary to the general thinning trend, approximately 21% of cases experienced cortical thickening. Similarly, around 50% of the sample showed cortical surface are increases during the study. These individual differences had a weak relation to age (for cortical surface), or no relation at all (for cortical thickness). Future research should investigate the between-individual characteristics related to this variability in change.

For example, recent research has shown that pubertal onset may be an important factor for cortical development, beyond the effect of age (Herting, Gautam, Spielberg, Dahl, & Sowell, 2015; Herting & Sowell, 2017; Juraska & Willing, 2017). The results from these studies suggest that sex differences in the production of hormones (particularly gonadal steroids; Juraska & Willing, 2017), together with individual differences in pubertal timing, may lead to different patterns of cortical reorganization in each person. Future research should investigate differences between males and females, and the role of puberty onset in the joint cognitive and cortical development. Studies including hormonal markers may help understanding the lead-lag sequences found in the present study, and search for differential cascade effects for boys and girls.

Relying on previous research, we have focused on a set of cortical regions studying whether cortical changes over time are associated with cognitive changes. It is possible that there is regional and functional specificity. For example, it is reasonable to think –and previous evidence suggests so– that the interrelations between cognitive and brain development may be even stronger for subsets of ROIs in the Basten et al. system (Pineda-Pardo et al., 2016). Finding patterns of regional specificity falls beyond the scope of this study and should be explored in future research. In a similar vein, the present findings do not provide enough evidence to think that the associations found are specific to the Basten set. Indeed, we found consistent results both for a set of regions identified in the P-FIT framework, and for the average CT and CSA for the whole brain (see supplementary materials). Similarly, including other neuroimaging measures, such as connectivity, or functional brain data from fMRI, will likely help understanding the interplay between the development of cognitive abilities and the relevant biological features involved.

Here we considered general cognitive ability. It would also be interesting to investigate the interplay between specific cognitive abilities –e.g., abstract reasoning, verbal ability, processing speed, working memory capacity– and brain development in those regions expected to be associated with them, and evaluate whether the results reported here are replicated with greater levels of granularity –i.e., Do increases in specific abilities predict cortical thinning in the relevant brain regions?

We chose a logarithmic transformation of age to account for potential nonlinear effects. However, other transformations of age could be suitable as well. Finding the most appropriate transformation of age for this type of developmental processes is an interesting research question that requires a formal investigation beyond the scope of the present study. Along the same lines, our selected model is –as every statistical model– a constrained representation of the phenomenon under study. As such, the excellent fit achieved does not imply that we were able to detect all possible age-related and developmental effects in the data.

Recent advances in continuous time modeling (Driver, Oud, & Voelkle, 2017; Estrada & Ferrer, 2019; Ji & Chow, 2018; Ou, Hunter, & Chow, 2017; Voelkle & Oud, 2015; Voelkle, Oud, Davidov, & Schmidt, 2012) allow a wide variety of possibilities for the study of dynamic systems. Applying these analytic frameworks could provide rich information about how the lead-lag effects between brain structure and cognitive ability change as a function of the time lag. Specifically, previous research has shown that different time sampling –and, therefore, different time lags– can lead to the identification of different self-feedback and coupling effects (Deboeck & Preacher, 2016; Voelkle et al., 2012). In our study, the time lag between measurement occasions was approximately two years for all participants and measures. This was due to the specific sampling schedule applied for acquiring the data. It is unknown whether the effects found here are due to the actual time-course of neurological pathways –i.e., reciprocal effects become manifest after approximately two years–, or they are due to working with these specific time lags. Continuous time models may help detecting more complex patterns of sequential effects for different time lags. On the other hand, the literature regarding these models is still scarce, and some features of our discrete time LCS –such as a measurement model with longitudinal factor invariance, or parameters capturing changes-to-changes influences– are not easy to implement in the current continuous time frameworks.

4.5. Conclusion

The key finding from the present research supports the general conclusion that individual differences in the changes in cognitive ability and cortical structure are partly explained by individual differences in their previous rates of change, and not their previous levels. Cognitive improvement is decelerated by previous cognitive improvements, but accelerated by cortical thinning and cortical surface reduction. In turn, cortical thinning is accelerated by previous cognitive gains. Based on this, we hypothesize that the (cross-sectional) associations found in previous studies might reflect reciprocal cascade effects from behavior to the neocortex and vice-versa.

These results suggest that, at least from childhood to early adulthood, we should pay attention not only to how able individuals become, but also to how fast they reach such cognitive level. Much is still unknown about what variables can explain the individual differences in the rate of cognitive improvement and cortical development. Some possible factors include genetic pathways, hormonal processes, brain features such as connectivity, or influences from the environment. Regarding the latter, the findings reported here may be helpful for designing environments able to foster sustainable increases in cognitive ability. Specifically, future programs designed for cognitive enhancement should test whether faster changes lead to stronger cortical reorganization, which, in turn, prevents subsequent fadeout effects.