New Generation of Mesoporous Silica Membranes Prepared by a Stöber-Solution Pore-Growth Approach

Abstract

Membranes consisting of uniform and vertically organized mesopores are promising systems for molecular filtration because of the possibility to combine high-flux and high-rejection properties. In this work, a new generation of mesoporous silica membranes (MSMs) have been developed, in which an organized mesoporous layer is directly formed on top of a porous ceramic support via a Stöber-solution pore-growth approach. Relevant characterization methods have been used to demonstrate the growth of the membrane separation layer and the effect of reaction time and the concentration of the reactants on the microstructure of the membrane. Compared to previous studies using the evaporation-induced self-assembly method to prepare MSMs, an important increase in water permeability was observed (from 1.0 to at least 3.8 L m^–2 h^–1 bar^–1), indicating an improved pore alignment. The water permeability, cyclohexane permporometry tests, and molecular cut-off measurements (MWCO ≈ 2300 Da) were consistent with membranes composed of 2–3 nm accessible pores.

1. Introduction

Many industrial process streams contain a mixture of water, solvents, and other organic components. The separation and recovery of these mixtures represent 40–70% of the total process costs.¹ To reuse these streams, purification is required and, to this end, membranes are increasingly applied.¹ Polymeric nanofiltration (NF) membranes that are commonly used today in wastewater treatment exhibit typically high permeability and stable rejection.^2,3 They offer a more sustainable and energy-efficient alternative to other separation technologies, such as distillation, evaporation, adsorption, extraction, and chromatography.¹ However, their application is limited to moderate temperatures, and to specific solvent and feed streams, which are not too aggressive.^4,5 The performances of polymeric membranes are often lost because of symptoms such as swelling and membrane breakdown.^4,5 This behavior hinders the implementation of the membrane technology in aggressive water/solvent mixtures.

On the other hand, ceramic NF and ultrafiltration (UF) membranes possess better properties such as high chemical, thermal, and mechanical stability, which makes them suitable for use in desalination and water treatment processes.⁵ Although SiO₂ and γ-Al₂O₃ membranes are less considered for water treatment and desalination applications, there is a growing interest in utilizing such membranes to address a variety of separation problems in miscellaneous industries.^6,7 Among these systems, silica membranes, consisting of ultra-small and uniform nanometer-sized pores/channels, are promising systems for molecular filtration separation because of the possibility to combine high-flux and high-rejection properties.⁸

The porosity, pore size, and tortuosity of acid-catalyzed sol–gel-derived silica layers can be tailored by incorporation of templating units during the synthesis.⁹ During further treatment, these templates are removed to generate corresponding pores in the final material. For example, on top of dense supports hexagonal lyotropic liquid-crystal mesophases can be obtained by the evaporation-induced self-assembly (EISA) method⁹ and perpendicularly oriented hexagonal channels are obtained.¹⁰ Unfortunately, on porous (ceramic) supports the structures tend to organize parallel to the surface instead of perpendicular because of unfavorable interactions between the material and the support surface.¹¹⁻¹³ Besides, these membranes are not always prepared in a reproducible way and possible formation of cracks was also observed. To solve this problem, the EISA method was applied to anodic alumina supports (AAS) having uniform cylindrical pores parallel to the transport direction.¹⁴⁻¹⁶ By using these supports, the authors were able to control the orientation of the pores during the drying process to form a silica nanochannel membrane (SNM) with a pore size varying from 3 to 15 nm. The perpendicular orientation of the silica nanochannels on the AAS was clearly demonstrated by transmission electron microscopy (TEM) analysis as well as the retention for various molecules (dyes, vitamins, and proteins) depending on the pore size.^14,15 Wooten et al.,¹⁷ prepared an SNM on top of an AAS using a neutral polymer to favor the orientation during drying. The membrane showed a solvent flux consistent with a vertical orientation of the pore channels. However, the orientation of the structure could not be investigated by structural characterizations techniques according to the authors. The pore orientation of the silica membrane was demonstrated by top-view SEM analysis, TEM analysis of the film, solvent flux, and solute rejection. Also, because of the brittle and fragile nature of the Whatman AAS, the SNM/AAS systems are not suitable for practical use in industrial applications.¹⁵ Besides, the SNM prepared by acid-catalyzed sol–gel are considered as hydro-instable because of the interaction of water molecules with the surface silanol groups.⁷

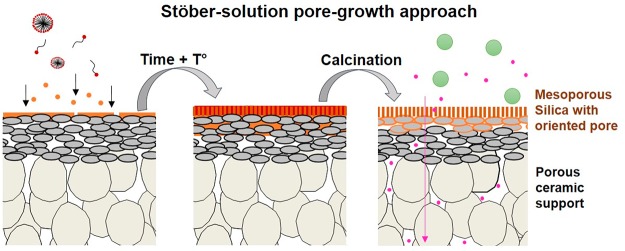
Recently, a method to synthesize uniform mesoporous silica nanospheres, the Stöber-solution pore-growth approach, was applied to develop mesoporous silica films.¹⁸ The Stöber-solution pore-growth approach can be used to control the pore formation of the layer by using a self-assembly process starting from an oil-in water basic-catalyzed sol–gel emulsion (or an oil-in-water Stöber sol). The use of a basic pH favors the condensation of silanols to siloxane bridges (Si–O–Si), and increases the hydro-stability of the silica material.⁷ Typically, thin mesoporous basic-catalyzed sol–gel-derived silica layers with perpendicular nanochannels were prepared on dense indium tin oxide (ITO) or silicon substrates by varying the reactants’ ratio [H₂O/EtOH/NH₄OH/tetraethoxysilane (TEOS)] or by adding oils (e.g., decane, ethyl ether, etc.).¹⁸⁻²⁴ Lin and co-workers¹⁹ were able to transfer silica nanochannel films (Ø_pore ≈ 3 nm) from ITO substrates to various porous substrates (i.e., porous silicon nitride, Ø_pore ≈ 4 μm, or polyethylene terephthalate, Ø_pore ≈ 2 μm) by using an elaborated film-assisted transfer approach. The orientation of the layer and the stability after calcination at 550 °C for 6 h or immersion in a hot piranha solution for 4 h was confirmed by TEM. The resulting SNMs exhibited a high selectivity toward molecules based on charge or size because of the very narrow channel size distribution (with an average diameter ≈2.3 nm). The same authors have also prepared a hydrophobic SNM by depositing a polydimethylsiloxane layer (≈1.3 nm thick) on top of freestanding or supported SNM. The membranes could filtrate molecules based on their hydrophobicity with an excellent selectivity.²⁰ However, the reproducibility of the SNM fabrication using the assisted film transfer procedure is around 80% and this percentage decreases with the increase of support roughness.¹⁹

Herein, we explore the possibility to use the Stöber-solution pore-growth approach to prepare SNMs directly on top of mesoporous γ-Al₂O₃ ceramic discs. Three different membranes were prepared using a CTAB/EtOH/TEOS aqueous ammonia solution to study the influence of the reaction time and amount of reactants. Special attention was devoted to a better understanding of the membrane formation and to determine the pore orientation by applying various characterization techniques. The uniformity and morphology of the layers were established using electron microscopy. The pore size was investigated by cyclohexane permporometry and polyethylene glycol (PEG) molecular weight cut-off (MWCO) measurements. The transport properties of the mesoporous silica membranes (MSMs) were studied by pressure-driven water permeation experiments.

2. Materials and Methods

2.1. Materials

TEOS (purity ≥ 99%), cetyltrimethylammonium bromide (CTAB) (purity ≥ 99%), ammonium hydroxide (28–30%), hydrochloric acid (37%), and absolute ethanol (purity ≥ 99%) were purchased from Merck. All water used is Milli-Q water. α-Alumina (α-Al₂O₃) supports (disc: 39 mm of diameter, 2 mm thick, 80 nm pore diameter) were purchased from Pervatech B.V., The Netherlands. One layer of γ-Al₂O₃ was deposited on top of the α-Al₂O₃ discs by dip-coating it in a boehmite sol in a dust-free room. The α-Al₂O₃ support was brought in contact with boehmite sol for 3 s and subsequently removed from the sol with an angular rate of 0.06 rad·s^–1. After calcination at 600 °C for 3 h, a 1.5 μm-thick γ-Al₂O₃ layer with an average pore diameter of 5.4 nm was obtained. The detailed fabrication procedure of this γ-Al₂O₃ layer can be found elsewhere.²⁵ PEG with various molecular weights (300, 600, 1000, 1500, and 3400 g·mol^–1) was purchased at Merck and used for the MWCO measurements. All chemicals were used as received without any further purification.

2.2. Preparation of Mesoporous Silica Membranes

2.2.1. Stöber-Solution Pore-Growth Method

MSMs were prepared based on procedures described in the literature for the Stöber-solution pore-growth method.^18,19 Flat mesoporous γ-Al₂O₃ ceramic discs were selected as support because of the possibility to conduct structural and morphologic analysis. A typical mixture consisted of 70 mL of water, 30 mL of ethanol, 10 μL (0.26 mmol) of ammonia, and 0.16 g (0.44 mmol) of CTAB first mixed at 60 °C for 30 min. Then, 80 μL (0.36 mmol) of TEOS was rapidly added to the solution under stirring. After 2 min of stirring, the solution was poured in a glass reactor containing a pristine γ-Al₂O₃-coated α-Al₂O₃ support and heated at 60 °C without stirring for 30 min (Figure S1). After a specific reaction time, the support was removed from the solution, rinsed with water, and aged at 100 °C for 8 h in air. The CTAB surfactant was then removed by immersing the MSM/γ-Al₂O₃ support into a 0.1 M HCl ethanol solution under moderate stirring for 10 min. This washing procedure was repeated two times. A final thermal treatment was carried out under N₂ at 500 °C for 1 h using a heating rate of 1 °C/min. Here, the calcination treatment was conducted to extract the possible remaining surfactant, and to increase the membrane stability by reactions between remaining silanols (Si–OH) with the γ-Al₂O₃ hydroxyl surface group. Total reactant volumes of 100 mL (condition A) and 200 mL (condition B) were used with reaction times of 15 h (for condition A and B) or 62 h (condition B). In total, at least four samples were prepared for each reaction condition. The reaction times, reaction volumes, and corresponding sample codes are reported in Table 1.

Table 1. Details of the Membrane Preparation for the Mesoporous Silica Membranes.

sample	total sol volume (mL)	reaction time (h)
MSM-A15	100	15
MSM-B15	200	15
MSM-B62	200	62

2.2.2. EISA Method

In order to compare the pore accessibility of the membranes developed with literature data, a membrane was prepared by the EISA method.²⁶ Flat mesoporous γ-Al₂O₃ ceramic discs were selected as support because of the possibility to conduct structural and morphologic analysis. The synthesis is carried out in two steps. A polymeric silica sol is first prepared by heating a mixture of 2.08 g (1 mmol) of TEOS, 5.5 g of ethanol, 0.5 g of water, and 0.4 g (0.1 M) of HCl at 70 °C for 1 h. After this time, the surfactant solution composed of 0.70 g (0.19 mmol) of CTAB dissolved in 10 g ethanol is added to the polymeric silica sol. After one additional hour of stirring at room temperature, the sol is deposited on a pristine γ-Al₂O₃-coated α-Al₂O₃ support by dip-coating (with dipping speed of 1.4 cm/s). After drying, the membrane was calcined in air at 500 °C for 4 h (heating rate = 1 °C/min) to remove the organic template. The membrane obtained was denoted MSM-EISA. SEM analysis of the MSM-EISA showed a uniform and separate top-layer with an average membrane thickness of ∼100 nm (Figure S2).

2.3. Membrane Characterizations

Field-emission scanning electron microscopy (FE-SEM) and scanning TEM (FE-STEM) images were obtained with a Zeiss MERLIN high-resolution scanning electron microscope using an accelerating voltage of 1.4 kV. FE-SEM samples were metalized by sputtering a layer of 1 nm chromium to favor charge release. The weight % of silicon, aluminum, and oxygen of the samples were determined by energy-dispersive X-ray spectroscopy (EDXS) using a Zeiss MERLIN at 10 kV with Oxford Instruments software. STEM-in-a-SEM specimens were prepared by placing drops of aliquots on a holey carbon-coated copper grid for TEM observation.

TEM was carried out with a Philips CM300ST-FEG TEM operated at 300 kV acceleration voltage, and equipped with a Noran System Six EDXS analyzer and Gatan Tridiem energy filter. EDXS was performed in point analysis mode at various locations along the cross section. The sample (MSM-B62 in this case) was prepared into a cross-sectional sandwich structure, by the method of dimple grinding/polishing and argon ion thinning, using on one side a piece of dummy silicon with a tungsten top-layer, glued onto the silica surface of a slice of the membrane sample. Argon ion thinning was done in a GATAN model 691 PIPS, using grazing angle beam incidence, that is, +4.5° for the upper gun and −2.5° for the lower gun. In order to minimize specimen damage, the energy of argon ion beam thinning the cross-sectional specimen was lowered from 4.0 keV to 700 eV in the final thinning stage.

X-ray diffraction powder patterns were recorded using a PANalytical X’pert MPD-Pro diffractometer at the wavelength of Cu Kα₁ (k = 1.5405 Å) (45 kV and 40 mA) in Bragg–Brentano scanning mode. The program scanned angles (2θ) from 0.5 to 10° with a 0.013° step, and a step time of 45 s.

Grazing incidence small-angle X-ray scattering (GISAXS) measurements were conducted on an Empyrean diffractometer. The wavelength of X-rays used was 0.154 nm and the angle of incidence was 0.2°. The scattering patterns were recorded with a 2-D detector.

The pore size of the MSMs was determined by permporometry measurements using cyclohexane as condensable vapor. The experimental procedure has been explained elsewhere.²⁷

2.4. Membrane Performance

Membranes were tested in a dead-end set-up for liquids, consisting of a stainless-steel feed vessel. During the water permeation/filtration tests, the temperature was kept at 25 °C. The feed vessel was connected to the inlet of the membrane module, which led to the active membrane area. The permeate was collected and weighed at specific intervals (every 30 min), while applying a nitrogen pressure of 8, 10, 12, 14, or 16 bar. The permeate was kept atmospheric. The water permeability [L m^–2 h^–1 bar^–1] was then calculated as the slope of the flux [L m^–2 h^–1] as a function of the trans membrane pressure (TMP) [bar]. Every water permeability measurement was performed at least on three samples prepared under the same reaction conditions. The water flux through the pristine γ-Al₂O₃ support and the MSM B62 membrane was found to be constant for a period of 2 h at a pressure of 8 bar (Figure S13).

On the basis of a procedure described in the literature,²⁸ retention analysis with aqueous PEG solutions (Merck) was done using PEGs with molecular masses of 300, 600, 1000, 1500, and 3400 g/mol in a dead-end filtration set-up at a TMP of 9 bar. A feed volume of 1 L was used with a concentration of 3 g/L (0.6 g/L for each PEG). During the experiment, the liquid was continuously stirred at 300 rpm in order to avoid the occurrence of concentration gradients. During each test, samples of the feed, retentate, and permeate solutions were collected once the flux reached a steady state (approximatively after 2 h, at around 10% recovery). Analysis of the composition of these samples was conducted by gel permeation chromatography (Agilent GPC, Water) (Figure S10). The molecular mass of the PEG corresponding to a 90% retention level was taken as the MWCO of the membrane. Every MWCO measurement was performed at least on two samples prepared under the same reaction conditions.

3. Results and Discussion

SEM observations were used to compare the morphology, location, and homogeneity of the pristine γ-Al₂O₃ support and the three silica mesoporous membranes. A SEM analysis of the top-surface of MSM-A15 (V_sol = 100 mL) revealed that the silica layer was inhomogeneous and did not completely cover the γ-Al₂O₃ layer (Figure 1, A.1 and A.2). Because of these inhomogeneities and noncomplete coverage of the MSM-A15, further performance studies were not done on this type of membrane. After doubling the amount of sol, the surface was completely covered with a homogeneous layer with a thickness of approximatively 25 nm (MSM-B15, Figure 1, C.1 and C.2). Additionally, the presence of nanoparticles was observed in and on the layer (≈100 nm in diameter, Figure 1, C.2) and on the edge of the support (≈150 nm in diameter, Figure 1, C.2) after an increase in total sol volume from 100 to 200 mL.

Figure 1.

Top-surface (A) and cross-sectional (B–D) FE-SEM images of the MSMs: MSM-A15 (A,B), MSM-B15 (C) and MSM-B62 (D). The numbers 1 and 2 refer respectively to a low and high magnification.

Increasing the reaction time from 15 to 62 h results in a growth of the layer from 25 to 50 nm (MSM-B62, Figure 1, D.1 and D.2). Moreover, no nanoparticles were detected on the majority of the samples (3–5 did not show any nanoparticles, whereas 2 showed few nanoparticles). The regularity of the thickness was confirmed by analyzing the sample at different spots and by comparison between samples prepared in similar conditions. The homogeneity of this layer was confirmed by an HR-based SEM analysis of the top-surface (Figure S4).

Concerning the nanoparticles observed in the sample MSM-B15 (Figure 1, C.2), there are similarities to those observed by Ma et al.²⁹ during the preparation of silica films on top of silicon wafers using an oil-in water basic catalyzed sol–gel emulsion. This emulsion was made by a self-assembly of gemini surfactants, costructure-directing agents, and silica precursors in the presence of ethanol as cosurfactant. The authors followed the layer formation by SEM analysis of the support cross section as a function of reaction time and concluded that growing started at “seed points” (spherical particles from 400 to 700 nm in diameter). The silica layer then grew and merged around these seed points. Thus, we assume that the particles visible in the MSM-B15 membrane layer (≈100 nm in diameter, Figure 1, C.2) could be attributed to “seed points” whereas the particles present on the surface could be considered as aggregates (≈150 nm in diameter, Figure 1, C.2).

To locate precisely the interface between the silica layer and the porous alumina support, an EDXS analysis of membrane cross sections was made (Figures 2 and S5–S7). This technique can also be employed to investigate the possible infiltration of silica into the porous γ-Al₂O₃ layer coated on the α-Al₂O₃ support. The EDXS analysis of the MSMs revealed the presence of silica in the γ-Al₂O₃ layer until the γ-Al₂O₃/α-Al₂O₃ interface, independently of the volume of sol used or reaction time. Unfortunately using this technique, it was impossible to differentiate precisely the composition of the top-layer from the γ-Al₂O₃ layer because of the low resolution.

Figure 2.

Cross-sectional FE-SEM image and EDXS maps of the MSM MSMB-62. The violet, red, and green dots represent the concentration of Si, O, and Al, respectively. The dashed white line represents the interface γ-Al₂O₃/α-Al₂O₃.

To determine at which stage of the reaction the impregnation of the silica in the γ-Al₂O₃ layer occurs, STEM imaging of aliquots of the reaction medium (Stöber sol) after different reaction times (45 min, 6 and 24 h) was conducted using a Zeiss MERLIN high-resolution scanning electron microscope (Figure S8). After 45 min of reaction, the presence of small particles (≈14 nm in diameter) was detected and the progressive formation of polydisperse silica particles (≈160–350 nm in diameter) with the increase of reaction time (from 6 to 24 h) was observed (Figure S8). Similarly, at a low ammonia concentration (0.5 M) and using the Stöber method, Han et al.,³⁰ demonstrated by STEM imaging the presence of clumps of loosely coalesced small particles (≈3–10 nm in diameter) after 10 min of reaction, which are gradually transformed to dense, polydisperse particles (≈300–400 nm in diameter after 6 h of reaction) as a function of the reaction time. The same authors confirmed that the growth mechanism of silica particles at a low ammonia concentration (≤0.95 M) using the Stöber process can be divided into two stages.³⁰ The first stage corresponds to the nucleation and fast growth of silica particles, and the second stage to a further growth of the silica particles. As the ammonia concentration is low, the TEOS hydrolysis (stage 1) is prolonged and continues in the second stage. As a result, unavoidable secondary nucleation of small silica particles is induced, which produces polydisperse silica particles. Considering the pore size of the γ-Al₂O₃ layer (≈5 nm in diameter), we can assume that impregnation of the silica occurred at the very first stage of the reaction and corresponds mainly to very small particles.

According to Teng and co-workers,¹⁸ the pore-growth of mesoporous silica films on glass or ITO dense support occurred through a slow conversion of silicate–CTAB composites from spherical to cylindrical micelles. In a first step, the surfactant cations (CTA⁺) are strongly adsorbed in the shape of micelles on the dense support which is negatively charged [the pH of the solution being superior to the point of zero charge (PZC) of the oxide surface]. Then, with the addition of TEOS molecules, a slow hydrolyzation of the precursor starts in the ammonia and ethanol solution, which leads to the formation of negatively charged oligomeric silicate species. These species approach the spherical micelle surface through electrostatic interaction, and are progressively deposited at the junction micelles/support. The presence of ethanol and ammonia contributes simultaneously to the transformation of the micelles from spherical to parallel mesochannels. With the continuous diffusion and re-assembly of CTAB molecules, newly hydrolyzed silicate oligomers are adsorbed, leading to continuous films with perpendicularly orientated pores.

On the basis of the above results of the STEM-in-a-SEM and SEM EDXS analysis, we propose that the pore-growth of the MSMs proceeds through a similar formation mechanism. Compared to the pore-growth of the mesoporous silica films, we propose that the growth of the membrane layer is induced by the seed points (i.e., spherical particles or impregnated particles) present in and/or on the negatively charged surface of the γ-Al₂O₃ layer (PZC ≈ 6–9). Thus, the existence of these seed points in the γ-Al₂O₃ layer requires to be studied in more detail. As the membrane MSMB-62 presents a negligible amount of aggregates on the surface, the chemical composition of the top-layer and the interface silica/γ-Al₂O₃ was analyzed in more detail by TEM combined with elemental distribution (Figure 4) and EDXS analysis (Figure 5).

Figure 4.

Energy-filtered TEM imaging of the MSM-B62 membrane cross section prepared by the FIB method: (A) bright-field TEM image; (B) elemental distribution. The green, pink, and blue dots represent the concentration of C, Si, and O, respectively.

Figure 5.

TEM image showing the cross section of the MSM-B62 membrane prepared by the method of dimple grinding/polishing and argon ion-thinning, indicating the different locations where local EDXS point analyses were carried out.

Because of the nature of the membrane sample (very thin MSM layer, high porosity, sensitive to primary electron beam irradiation), two sample preparation methods were tested and compared to exclude the potential presence of artefacts in the TEM imaging and EDXS analysis. The first cross-sectional specimen was created via mechanical polishing, that is, the method of dimple grinding/polishing followed by low-energy argon ion-thinning. The second cross-sectional specimen was made by the focused ion beam (FIB). In order to reduce beam-induced artifacts, we applied a kind of low-dose technique, that is, moving the specimen to the area of interest, perform precise focusing there, but recording a TEM image in a fresh unexposed area next to it.

Figure 3 shows a cross-sectional TEM image of the MSM-B62 membrane, prepared by FIB, with five different layers. The two layers on the top, denoted as platinum and carbon, are used to protect the top-layer from destructive gallium ion-etching. The next layer is a 20 nm thick silica top-layer, and below that a 40 nm thick interfacial layer is observed. The total thickness of these two layers (50–60 nm) is in accordance with the FE-SEM results, showing an approximately 50 nm thick top-layer (Figure 1, D.1 and D.2). The last layer is a γ-Al₂O₃ layer showing the typical microstructure of a γ-Al₂O₃ layer.¹²

Figure 3.

TEM image showing the cross section of the MSM-B62 membrane prepared by the FIB method.

To characterize the chemical composition of the top-layer and the interface silica/γ-Al₂O₃, an energy-filtered TEM analysis was conducted. This method has the advantage of demonstrating precisely the chemical composition by mapping. Figure 4B shows the results for the MSM-B62 membrane. As can be seen from this figure, silicon is predominantly present in the first 40 nm of the membrane top-layer. A distinction in composition between the top- and interlayers was however unclear. With the aim of characterizing the chemical composition of the top-layer, an additional EDXS elemental point analysis was performed (Figure 5).

The Si/Al atomic ratios were measured at three different locations, and are listed in Table 2 [top of the layer (pt. 1), interface (pt. 2), and γ-Al₂O₃ (pt. 3)]. From these results, it is concluded that the interfacial layer and the top-layer have the predominant composition of a silica layer (Si/Al respectively 5.3 and 1.6 as evidenced by EDXS).

Table 2. Atomic Compositions of the Different Layers Observed in the MSM-B62 Membrane.

pt.	locations	Si/Al atomic ratio
1	top-layer	5.3
2	connection interfacial layer/γ-Al2O3	1.6
3	γ-Al2O3	0.33

To study the pore size of the membranes several methods were used. First, cyclohexane permporometry experiments were conducted.²⁷ The oxygen flux through the MSMs (MSM-B15 and MSM-B62) and the pristine γ-Al₂O₃ support as a function of the relative cyclohexane pressure during the desorption step is shown in Figure S9 of the Supporting Information. In the interval 0.8 > P/P₀ > 0.45, all pores are blocked with condensed cyclohexane and free oxygen diffusion is impeded. At relative pressures between 0.55 and 0.3, the oxygen permeance increases with an increasing number of open pores for the pristine γ-Al₂O₃ support [from 8 × 10^–8 to 1.7× 10^–7 mol/(s m² Pa)]. Assuming that the capillary condensation process takes places in this interval, a Kelvin diameter of 5.4 nm was calculated for the pristine γ-Al₂O₃ support. For the MSM-B15 and MSM-B62 membranes, a reduction of the relative pressure from 0.3 to 0.2 leads to an increase of the oxygen flux [from 4 × 10^–8 to 1.6 × 10^–7 mol/(s m² Pa)]. These results suggest first that the silica particles present in the γ-Al₂O₃ layer did not block the pores. Second, the results for each MSM are very similar, which confirms that the aggregates present on the surface of MSM-B15 do not affect the pore size of the membrane. Thus, if we apply the Kelvin equation at a P/P₀ ≈ 0.2, the average pore diameter of the MSMs is between 2 and 3 nm (MSM-B15: 2.6 ± 0.4, MSM-B62: 3.0 ± 0.2, the results are averaged from at least three samples and the error bars are standard deviations). These values are in accordance with the pore size estimated in literature for mesoporous silica films prepared on dense substrates by the Stöber-solution pore-growth approach (≈2 nm by TEM or N₂ sorption analysis of freestanding films).^18,19

The pore size of the membrane can also be examined using retention tests of a series of PEG molecules with different molecular weights. These molecules are used commonly to evaluate the molecular-weight cutoff of UF membranes.⁴Figure 6 shows the PEG retention obtained for the MSM-B15 and MSM-B62 membranes. For both MSM membranes an identical MWCO of ∼2250 Da was observed (Figure 6). According to Puhlfürß et al.,³¹ the molecular weight of PEG can be correlated to the Stokes–Einstein radius of the molecules using the following equation

1

Figure 6.

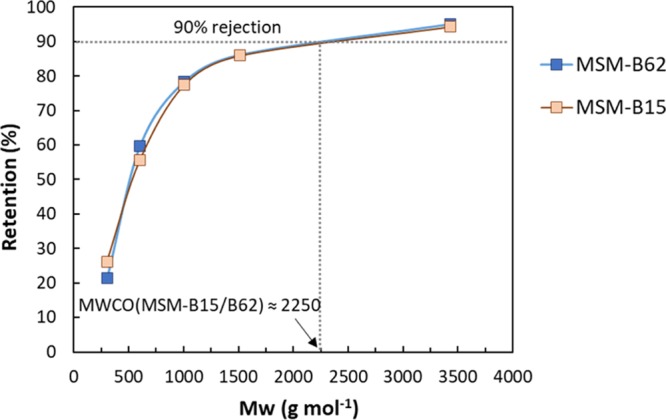
PEG MWCO measurements for the MSMs: MSM-B15 and MSM-B62. PEG retention results are averaged from two samples for the MSM-B15 membrane and three for the MSM-B62. Using standard deviations, the highest retention error bars obtained was 8%.

In this way, we have calculated the hydrodynamic diameters (d_H) of 2.5 nm related to the molecular weight at 90% retention (2250 Da) of the MSM systems. This value corresponds with the pore size as determined by cyclohexane permporometry, and confirms the uniformity in pore size of both samples.

In the case of mesoporous silica thin films prepared on dense substrates, the vertical alignment of the pores to the support surface has been demonstrated in literature by direct characterization techniques such as TEM, low-angle X-ray diffraction (XRD) and GISAXS.¹⁸⁻²⁰ These techniques are used to show the perpendicular orientation of the mesochannels and also the hexagonal structure of the film.¹⁸⁻²⁰ However, in our work neither TEM, low-angle XRD, nor GISAXS analysis gave conclusive results for the MSM prepared in this study. The inconclusive results in TEM are maybe because the silica layer is easily affected by the high-energy primary electron beam. Concerning the X-ray analysis, the absence of diffraction peaks could be explained by the presence of perpendicular pores or a disordered layer (Figure S11).¹⁷ Thus, the membrane was investigated by GISAXS. Unfortunately, independent of the parameters sets, only one reflection center at the same position as the grazing incidence X-ray beam was observed (Figure S12). The absence of second diffraction sheets was attributed to the roughness of the support and porosity of the γ-Al₂O₃ underlayer. A similar problem for characterization was evidenced for membranes, prepared by the EISA method on top of the AAS by Wooten et al.¹⁷ They, therefore, studied the pore orientation of the mesoporous silica layer through an ethanol flux permeability study.¹⁷

In our study, water flux measurements were conducted on the MSM as an indirect characterization of the pore accessibility of the membrane (i.e., pores vertical- or parallel-oriented to the surface or of a distorted structure). Figure 7 shows the clean-water flux as a function of the applied TMP, ΔP (from 7 to 15 bar) through the pristine α-Al₂O₃ and γ-Al₂O₃ layer coated on the α-Al₂O₃ supports, and the MSMs MSM-B15 and MSM-B62. The measurements were also conducted on the additional membrane MSM-EISA prepared for comparison with the EISA method. As explained in the Introduction section, membranes prepared by the EISA method on top of porous γ-Al₂O₃-coated α-support tend to have pores organized parallel to the surface. The water permeability for each sample was estimated from the slopes of the TMP versus flux curve. The water permeabilities obtained for the pristine α-Al₂O₃ and γ-Al₂O₃ supports are in line with previous studies on similar supports.^13,36 The small difference denoted can be explained by the difference of membrane thickness and thermal treatment.³⁶ These values are two times higher than the results of the MSM-B15 and MSM-B62 membranes. The water permeabilities obtained for the MSM-B15 and MSM-62 are almost identical, suggesting that the aggregates on top of the MSM-B15 membrane or the difference in thickness between the two membranes (∼25 nm) does not influence the water flux. Compared to the MSM prepared by the EISA method, an MSM from the Stöber-solution pore-growth approach shows a significant increase of the water permeability, from 1.0 to at least 3.8 L m^–2 h^–1 bar^–1. A previous study on the MSM prepared by the EISA method revealed that the water permeability was around 1.5 L m^–2 h^–1 bar^–1 for parallel-aligned nanochannels.¹³

Figure 7.

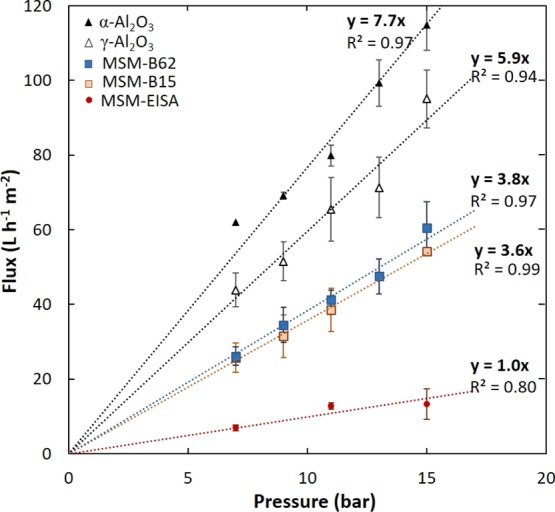
Water flux vs TMP for the α-Al₂O₃ and γ-Al₂O₃ layer coated on the α-Al₂O₃ pristine supports, and the MSMs (MSM-B15, MSM-B62, and MSM-EISA). Flux error bars were obtained using the standard deviation on at least three different samples.

As the morphology of the top-layer on a ceramic porous support cannot be measured with a direct technique, a model was developed to get a better understanding of the morphology [e.g., the tortuosity and pore orientation (parallel or vertical) of the top-layer] prepared via the EISA and the Stöber-solution pore-growth approach. The model is based on the viscous flow model.¹³ The solvent flux through mesoporous membranes is assumed to be proportional to the applied pressure difference, irrespective of the type of liquid used.^32,33 In this transport mechanism, the overall liquid permeability coefficient of each membrane (or permeability constant), k_m (m), can be expressed as the product of the volumetric flux, J (m·s^–1), and the solvent viscosity, η (bar·s), divided by the transmembrane pressure applied, ΔP (bar).¹³

2

The overall permeability coefficient can be described as the sum of different resistances. In a γ-Al₂O₃ membrane coated on a α-Al₂O₃ support, the overall water permeability can be divided into two resistances in parallel and can be expressed as follows

3

with k_α, and k_γ being the permeability coefficient of the α-Al₂O₃ support and the γ-Al₂O₃ layer. In the cases of an MSM prepared by the EISA method, if there is no infiltration of silica particles into the γ-Al₂O₃ layer, the overall water permeability can be divided into three resistances in parallel

4

with k_Si being the permeability coefficient of the mesoporous silica layer. When some silica particles are present in the γ-Al₂O₃ layer (like in the MSM-B15 or MSM-B62 membranes), the overall membrane permeability can be described depending of the proportion of silica present in the γ-Al₂O₃ layer, as

5

or

6

with k_Si/γ being the permeability coefficient of the γ-Al₂O₃/SiO₂ layer.

Also, under conditions where Darcy’s law is valid, the permeability coefficient of a single layer k_L can be given by

7

where ε is the porosity of the membrane material, τ is the tortuosity of the pore structure, L is the layer thickness, and r is the pore radius. The porosity values for the membrane material are estimated from nitrogen sorption data on flakes and previously reported in literature (≈58% for the MSMs and 55% for the γ-Al₂O₃ layer).^34,35

First, the water permeability coefficient was calculated after plotting the product of the viscosity by the water flux as a function of the transmembrane applied pressure for each membrane (α-Al₂O₃, γ-Al₂O₃, MSM-B15, MSM-B62, and MSM-EISA) (Figure S14). The water permeability coefficient for the α-Al₂O₃ support (k_α) was 1.8 × 10^–14 m and it is assumed that this value is identical for each membrane. So, the influence of permeability of the support is in all cases identical and is therefore assumed as a constant.

To check the model, for a γ-Al₂O₃ membrane (Figure 8A), the individual water permeability coefficient (k_L) of the γ-Al₂O₃ layer can be calculated using eq 3 and the k_α value determined with eq 2. As a result of this, the tortuosity can be calculated for the γ-Al₂O₃ layer using eq 7, by considering different layer thicknesses (L: 1.2, and 1.5 μm) and pore diameters (Ø_γ from 3.5 to 5.4 nm). Figure 8B shows a plot of the calculated water permeability coefficient (k_m) values as a function of tortuosity of the γ-Al₂O₃ layer (from 1 to 20) for five different membranes. The water permeability coefficient clearly decreases with increasing tortuosity and thickness and decreasing pore size (Figure 8B). More importantly, the experimental and predicted values for the pristine γ-Al₂O₃ membrane used in this study (L: 1.5 μm, Ø_γ: 5.4 nm) converge, assuming a tortuosity of 5.9. The tortuosity of the pristine γ-Al₂O₃ membrane falls in the range of tortuosities reported in the literature for γ-Al₂O₃ membranes calcined at 600 or 800 °C (between 5 and 13).^35,36 Thus, we can conclude that the model works in explaining the experimental results obtained and could be used to study the MSM.

Figure 8.

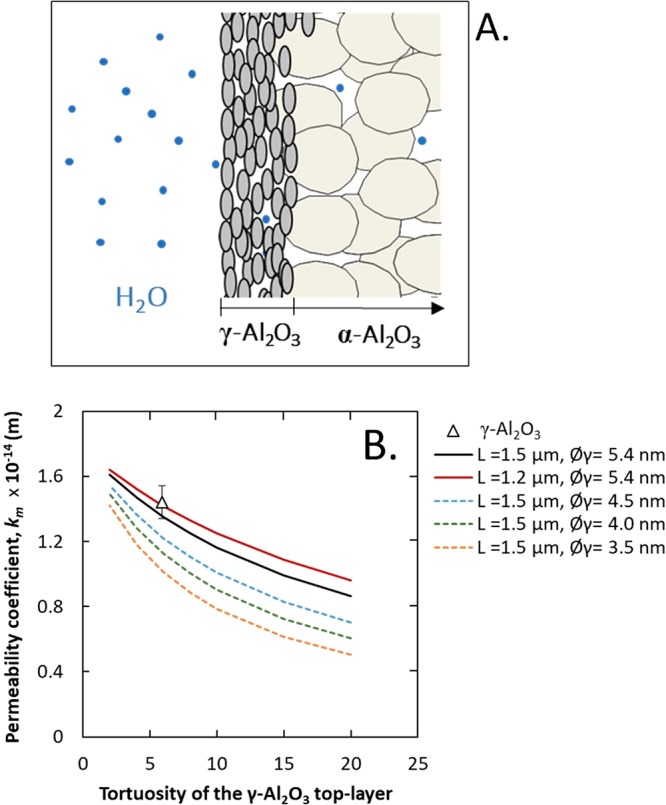
(A) Schematic representation of the γ-Al₂O₃ membrane configuration; (B) predicted and experimental water permeability coefficient vs tortuosity for separation layers with varying thicknesses (L) and pore sizes (Ø_γ). The experimental water permeability coefficient value is averaged from five γ-Al₂O₃ samples, and the error bar values were obtained using standard deviation.

For the MSM prepared by the EISA (MSM-EISA) method and the Stöber-solution pore-growth method (MSM-B62), it was not possible to calculate the permeability coefficient by using eqs 3 and 4 or 5 because of the presence of too many unknowns. Therefore, four different membrane configurations were considered (Figure 9). The first case corresponds to an MSM with pores parallel to the membrane surface, the second case to an MSM with perpendicular-oriented pores, the third and fourth cases correspond to membranes consisting of an MSM layer with perpendicular-oriented pores and with silica particles infiltrated respectively partially or totally in the γ-Al₂O₃ layer.

Figure 9.

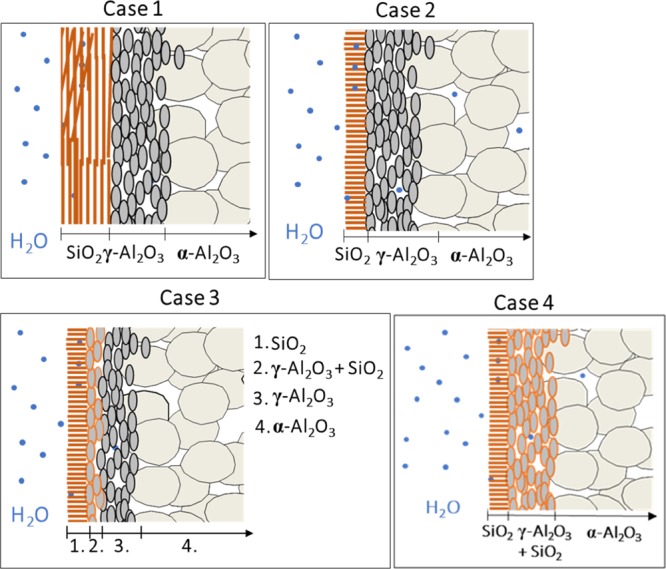
Schematic representation of the different possible membrane configurations: an MSM with parallel pores to the surface (case 1), an MSM with perpendicular-oriented pores and without infiltrated silica particles (case 2), an MSM with perpendicular-oriented pores with partial (case 3) or total infiltration of silica particles (case 4) into the γ-Al₂O₃ layer.

For these four different cases the combined effect of variables in the morphology (tortuosity, layer thickness, and pore size) on the water permeability coefficients (k_m) is depicted in four graphs (Figures 10 and 11).

Figure 10.

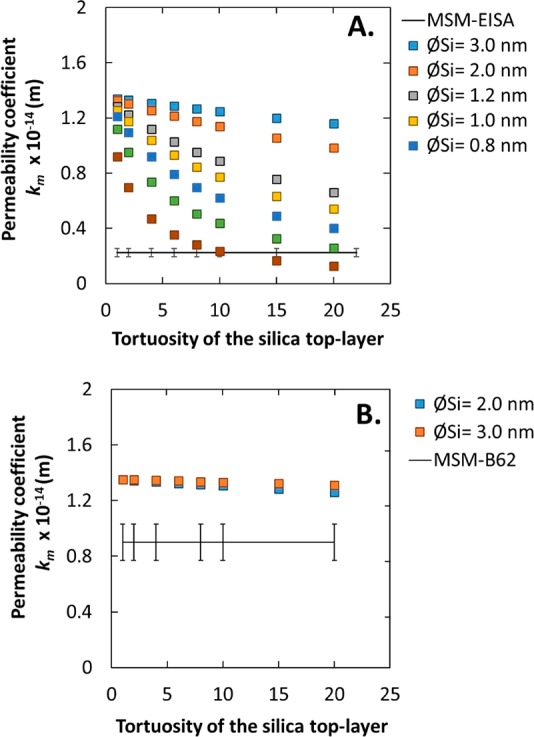
Predicted water permeability coefficient values vs tortuosity of the silica top-layer, without infiltration of silica into the γ-Al₂O₃ layer. (A) Silica layer thickness L = 100 nm; predicted values are compared with results of MSM-EISA membranes. (B) Silica layer of 20 nm; experimental results are from MSM-B62.

Figure 11.

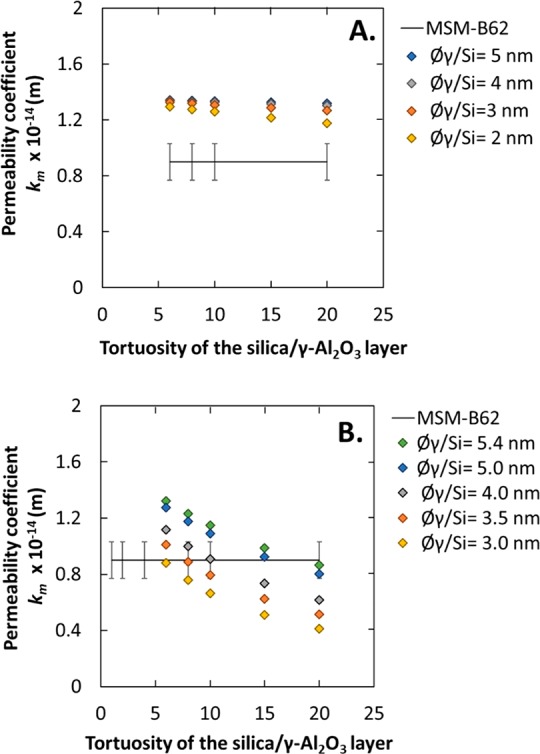
Predicted water permeability coefficient vs tortuosity of the silica top-layer (thickness: 20 nm) with infiltration of silica into the γ-Al₂O₃ layer. (A) Partial infiltration, L = 40 nm. (B) Total infiltration, L = 1.5 μm. In both cases, the experimental results of MSM-B62 membranes are given.

3.1. Case 1: MSM with Pores Parallel to the Surface

In this case, the membrane consists of separate α-Al₂O₃, γ-Al₂O₃, and silica layers and can be described using eq 3 which is composed of three resistances related to each layer. In this equation only the resistance (pore size and tortuosity) of the silica layer is unknown. Thus, in the next calculation we have considered five membranes with pore size between 0.6 and 3 nm and tortuosity between 1 and 20. The water permeability coefficients (k_m) are plotted as a function of tortuosity of the silica top-layer based on eqs 4 and 7 in Figure 10A. The silica layer thickness is fixed at 100 nm, as being the thickness of the EISA separation layer. The experimental permeability fits with the predicted permeability for an MSM-EISA membrane of 0.6 nm in pore size and a tortuosity of more than 20. This result is in accordance with the permporometry analysis, which suggests the presence of micropores <1 nm (Figure S3). Similarly, Klotz et al.,¹² demonstrated that an MSM membrane prepared by the EISA method showed a gas transport through the microporous silica walls instead of through the mesopores because of the alignment of the pores parallel to the support surface. Thus, the low permeability values obtained for the MSM-EISA sample and the possible presence of micropores suggest a transport of the water molecules through the microporous silica walls of the material instead of through the mesopores. The predicted and experimental values confirmed here the alignment of the mesopores parallel to the support surface for the MSM-EISA sample.

3.2. Case 2: MSM Layer with Perpendicular-Oriented Pores without a Silica-Infiltrated γ-Al₂O₃ Layer

In this case the membrane consists of α-Al₂O₃, γ-Al₂O₃, and silica layers and can be described using eq 3 which is composed of three resistances related to each layer, with the same unknowns. Thus, in the next calculation we have considered two silica membranes consisting of perpendicular-oriented pores with a diameter of 2 or 3 nm and a tortuosity between 1 and 20. The calculated water permeability coefficients (k_m) of two different membranes are plotted as a function of tortuosity of the silica top-layer (from 1 to 20) based on eqs 4 and 7 in Figure 10B. The layer thickness of the silica top-layer is 20 nm (determined by TEM for MSM-B62) with a pore size (Ø_Si) of 2 or 3 nm (as determined by permporometry and PEG MWCO). With the increase of tortuosity from 1 to 20, the water permeability coefficient decreases slightly from 1.4 to 1.3 or 1.2 × 10^–14 m. The calculations showed that an MSM with vertically organized channels (tortuosity ≈1) should result in a water permeability coefficient of 1.3 or 1.4 × 10^–14 m, which is very close to the value obtained for a pristine γ-Al₂O₃ membrane (1.4 × 10^–14 m). In order to see if the water permeability coefficient of membrane MSM-B62 is consistent with vertically organized pores, the result for this membrane is given as well. The experimental value did not converge with any of the predicted values. An explanation for this difference could be the infiltration of Si in the γ-Al₂O₃ layer (as observed by EDXS analysis), resulting in a possible reduction in the pore size of the γ-Al₂O₃ layer. Therefore, cases 3 and 4 are investigated.

3.3. Case 3: MSM Layer with Perpendicular-Oriented Pores and Silica Partially Infiltrated in the γ-Al₂O₃ Layer

As observed by the TEM-EDXS analysis, the first 40 nm of the γ-Al₂O₃ layer has a higher percentage of silica than the rest of the layer (a Si/Al ratio of 1.5 and then 0.3). In this case, the membrane consists of α-Al₂O₃, γ-Al₂O₃, γ-Al₂O₃/silica, and silica layers and can be described using eq 5 which is composed of four resistances related to each layer. In this equation, the MSM layer is assumed to consist of perpendicular-oriented pores, thus a tortuosity of 1 (τ), and a pore size (Ø_Si) of 3 nm were used to predict the permeability coefficient of this layer (k_Si). To determine the permeability coefficient of the silica/γ-Al₂O₃ layer, k_Si/γ, we made the assumption that the tortuosity should have the same value as the pristine γ-Al₂O₃ layer (≈6) whereas the pore size could be less than that of the pristine γ-Al₂O₃ layer (<5.4 nm). For the γ-Al₂O₃ layer without infiltrated silica particles, the permeability coefficient (k_γ) was estimated using a thickness of 1.46 μm. Only the resistance (pore size and tortuosity) of the γ-Al₂O₃/silica layer is unknown. Thus, in the next calculation we have considered four membranes with a pore size of 2, 3, 4, or 5 nm and tortuosity between 6 and 20. Using eq 5, the calculated overall water permeability coefficient values obtained as a function of the tortuosity of the silica/γ-Al₂O₃ layer are reported in Figure 11A. The decrease in pore size of the silica-infiltrated γ-Al₂O₃ layer results in a slight decrease of the permeability coefficient when compared to non-silica-infiltrated layers (Figure 10B). None of the values converge with the experimental permeability coefficient of the MSM-B62 membrane, which suggests that the effect of the infiltrated silica particles is more significant than expected. An explanation of this could be that the percentage of silicon found by TEM–EDXS is underestimated. Assuming a reduction in pore size of the entire γ-Al₂O₃ layer, case 4 was considered.

3.4. Case 4: MSM Layer with Perpendicular-Oriented Pores and Silica Infiltrated Totally in the γ-Al₂O₃ Layer

Assuming that the silica particles infiltrate homogeneously into the γ-Al₂O₃ layer, the tortuosity should stay constant (≈6), whereas the pore size decreases (<5.4 nm). In this case, the membrane consists of α-Al₂O₃, γ-Al₂O₃/silica, and silica layers and can be described using eq 6 which is composed of three resistances related to each layer. In this equation, the MSM layer is assumed to consist of perpendicular-oriented pores, thus a tortuosity of 1 (τ) and a pore size (Ø_Si) of 3 nm were used to predict the permeability coefficient of this layer (k_Si). Only the resistance (pore size and tortuosity) of the γ-Al₂O₃/silica layer is unknown. Thus, in the next calculation we have considered five γ-Al₂O₃/silica layers with a pore size of between 3.0 and 5.4 nm and tortuosity between 6 and 20, whereas the layer thickness was kept at 1.46 μm (eq 7). The calculated overall water permeability coefficient values obtained as a function of tortuosity are reported in Figure 11B. The decrease in pore size of the silica-infiltrated γ-Al₂O₃ layer results in a significant decline in water permeability coefficient as compared to the case where the silica/γ-Al₂O₃ layer was only 40 nm in thickness (case 3, Figure 11A). Here also the calculated results were compared with the MSM-B62 membrane. The experimental water permeability fits with most of the predicted water permeability curves, which confirms the decrease of the pore size of the total γ-Al₂O₃ layer.

To conclude, after thoroughly studying the morphology of the silica membranes prepared by the Stöber-solution pore-growth approach it can be concluded that the membrane shows significantly increased flux compared to the MSM-EISA type of membrane. As the hydrophilic nature of the membranes was confirmed in each case by water contact angle measurements (Figure S15), we can conclude that the increase of flux is due only to an increased accessibility of the pores. With the aim of obtaining the highest flux as possible, further research to prevent the infiltration of the silica into the γ-Al₂O₃ layer should be conducted. Using this permeability coefficient prediction model, it will be possible to determine the tortuosity of the silica top-layer and give more insight into the alignment of the pores.

On the basis of the above results and proposed mechanism of Teng and co-workers,¹⁶ we assume that the Stöber-solution pore-growth, resulting in an MSM occurs through a step by step mechanism. In the first stage of the reaction, the porous γ-Al₂O₃ support is immersed in the surfactant aqueous-ethanoic solution at a pH of ≈11. At this pH, the γ-Al₂O₃ porous support is negatively charged (PZC of alumina ≈ 6–9), and the surfactant cation heads (CTA⁺) are strongly adsorbed on the support surface in the form of spherical micelles (step 1, Figure 12). After addition of the TEOS, the first primary silica particles are rapidly formed as shown in the STEM analysis of the sol (Figure S8). As assumed, these particles diffused into the γ-Al₂O₃ layer and are adsorbed in and on the support surface. These particles act as seed points for the growth of the MSMs (step 2, Figure 12). With time, the rest of the TEOS molecules are slowly hydrolyzed in solution; the resulting negatively charged oligomeric silicate species approach the spherical positively charged micelle and the junction seeds/support (steps 2 to 3, Figure 12). As mentioned before, the presence of ethanol and ammonia contributes simultaneously to the transformation of the micelles from spherical to parallel mesochannels (step 3). With the continuous diffusion and re-assembly of the surfactant molecules, newly hydrolyzed silicate oligomers are adsorbed, leading to a continuous membrane with accessible pores after calcination (step 4).

Figure 12.

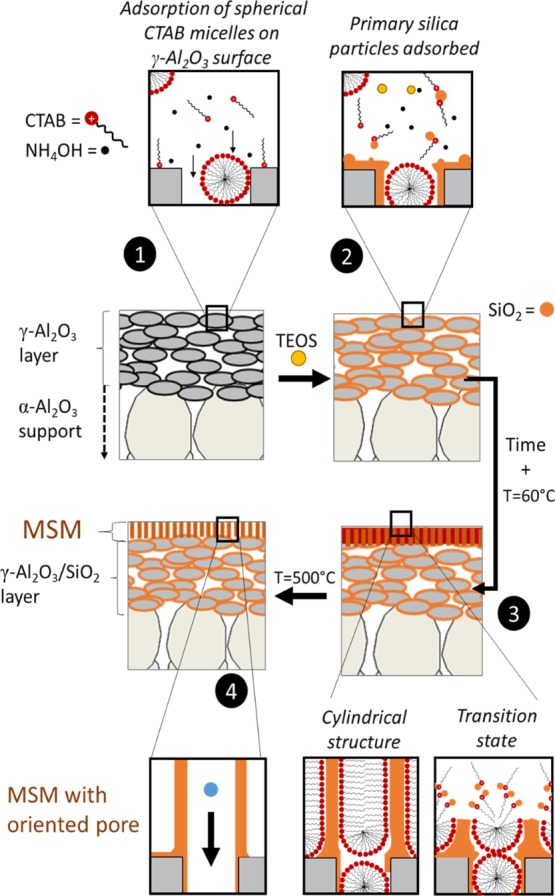
Illustration for the formation process of the ordered MSM by the Stöber-solution pore-growth approach (adapted from ref (16)).

4. Conclusions

A Stöber-solution pore-growth approach was used to prepare thin and homogeneous silica mesoporous membranes. An increase in the reaction time from 15 to 62 h results in a growth of the layer thickness from 25 to 50 nm. Also, it was observed that the presence of aggregates (100–300 nm) did not affect the membrane pore size (2–3 nm) or water permeability performance, which in all cases was ∼3.8 L·m^–2·h^–1·bar^–1. This permeability is three times higher than the state-of-the-art MSMs prepared via the EISA method.

At the beginning of the synthesis silica particles with a very small diameter are formed and infiltration of these small particles into the γ-Al₂O₃ layer is observed, resulting in a significant decrease of the pore size of this layer.

The alignment of the pores was studied with direct techniques such as GISAXS, TEM, and low-angle XRD. However, because of the rough surface and porous nature of the support, the results were inconclusive. Indirect techniques were used to gain insight into the morphology. A water permeability model was developed to indicate the pore size and tortuosity of the developed MSMs. This model gives an indication of the amount of silica particles infiltrated in the γ-Al₂O₃ layer of the membrane substrate. Finally, it can be concluded that the alignment of the pores is significantly improved by using the Stöber-solution pore-growth approach when compared with EISA-derived silica membranes.

Moreover, owing to its preparation, good PEG separation performance, and superior water flux, this MSM shows great potential in practical applications. Furthermore, the Stöber-solution pore-growth approach is also likely to be applicable to hybrid silica precursors and open up new possibilities to study the formation of stable membrane based on periodic mesoporous organosilica.

Glossary

Abbreviations

NF

nanofiltration

UF

ultrafiltration

MSMs

mesoporous silica membranes

EISA

evaporation-induced self-assembly

AAS

anodic alumina supports

SNM

silica nanochannel membrane

MWCO

molecular weight cut-off

CTAB

cetyltrimethylammonium bromide

TEOS

tetraethoxysilane

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.9b03526.

• Schematic illustration of the set-up use for the Stöber-solution pore-growth synthesis, SEM and permporometry analysis of the MSM-EISA sample; top-surface SEM pictures of the sample MSM-B62; EDXS analysis of the pristine γ-Al₂O₃ support, and the MSM-A15 and MSM-B15 membranes; STEM analysis of the particles in the sol as a function of the reaction time; graphic from the permporometry analysis for the pristine γ-Al₂O₃ support and the MSM-B15 and MSM-B62 membranes; permeate and retentate curves from the PEG retention measurements; low-angle XRD analysis of the sample MSM-B62; 2D-GISAXS scattering profiles of the sample MSM-B62; graphic of the water flux vs measurement time through the pristine γ-Al2O3 support and the MSM-B62 membrane; graphic of the water flux by the viscosity versus applied pressure; and water contact angle measurements of the membrane MSM-EISA and MSM-B62 (PDF)

This work is part of the research program titled “Organic solvent NF membranes on low cost ceramic supports” (BL-30-01), which is taking place within the framework of the Institute for Sustainable Process Technology (ISPT) and is partly financed by the Topsector Energy subsidy of the Ministry of economic affairs in The Netherlands.

The authors declare no competing financial interest.