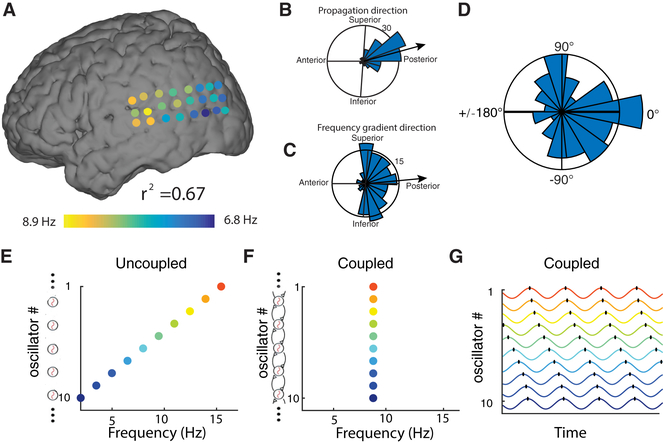
Figure 7: Mechanisms of traveling waves.

(A) The instantaneous frequency distribution across an oscillation cluster from Patient 1 on one trial (same as Fig. 1B), demonstrating an anterior-to-posterior decreasing spatial-frequency gradient (r² = 0.67). (B) Distribution of traveling-wave propagation directions on this electrode cluster across trials (reproduced from Fig. 1G). (C) Distribution of the directions of the spatial-frequency gradients across this cluster. In B & C, black lines indicate the mean directions, thus demonstrating a correspondence between the directions of phase and frequency gradients. (D) Distribution of angular differences, across oscillation clusters, between the mean direction of traveling-wave propagation and the mean direction of spatial frequency gradients. (E–G) Illustration of a model of weakly coupled oscillators (Ermentrout and Kopell, 1984) with parameters matched to our findings. Color warmth increases with intrinsic frequency. When there is no phase coupling (Panel E), individual oscillators demonstrate their intrinsic oscillation frequencies from 2 Hz (anterior) to 16 Hz (posterior). When phase coupling is present (Panels F–G), all oscillators have the same temporal frequency (F) and a traveling wave emerges (G).