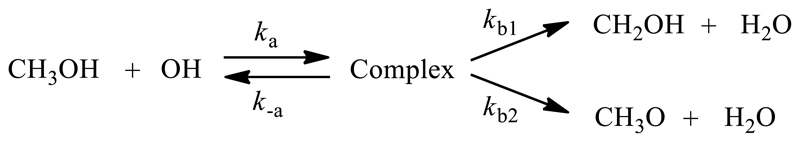Gas-phase reactivity of CH₃OH toward OH at interstellar temperatures (11.7-177.5 K): Experimental and theoretical study

Abstract

The reactivity of methanol (CH₃OH) toward the hydroxyl (OH) radical was investigated in the temperature range 11.7 – 177.5 K using the CRESU (French acronym for-Reaction Kinetics in a Uniform Supersonic Flow) technique. In the present study, the temperature dependence of the rate coefficient for the OH+CH₃OH reaction, k(T), has been revisited and additional experimental and computational data are reported. New kinetic measurements were performed to fill the existing gaps (<22 K, 22-42 K and 88-123 K), reporting k(T<20 K) for the first time. The lowest temperature ever achieved by a pulsed CRESU has been obtained in this work (11.7 K). k(T) abruptly increases by almost 2 orders of magnitude from 177.5 K to around 100 K. At T<100 K, this increase is less pronounced, reaching the capture limit at temperatures below 22 K.

The pressure dependence of k(T) has been investigated for selected temperatures and gas densities (1.5×10¹⁶ to 4.3×10¹⁷ cm^-3), combining our results with those previously reported. No dependence was observed within the experimental uncertainties below 110 K. The high- and low-pressure rate coefficients, k_HPL(T) and k_LPL(T), were also studied in detail using high-level quantum chemical and theoretical kinetic methodologies, closely reproducing the experimental data between 20 and 400K. The results suggest that the experimental data are near the high pressure limit at the lowest temperatures, but that the reaction remains a fast and effective source of CH₂OH and CH₃O at the low pressures and temperatures prevalent in the interstellar medium.

1. Introduction

Methanol (CH₃OH) and hydroxyl (OH) radicals are relatively abundant in cold and dense interstellar clouds and are two important species for the interstellar chemistry. CH₃OH is well-known as a starting point for the formation of more complex organic molecules (COMs) in these molecular clouds^1–3 and OH is a key intermediate molecule there.^4–7 Thus, the reactivity of CH₃OH toward OH may play a crucial role in the formation of other species in the ISM and reliable rate coefficients should be used in astrochemical models describing low temperature reaction networks.

Three general cases for exothermic reactions can be identified:⁸ (i) the reaction presents a substantial energy barrier caused by the necessity to break chemical bonds; (ii) the reaction presents no barrier on the potential energy curve; (iii) the reaction possesses a pre-reactive weakly bound complex which then crosses an activation barrier, submerged or not with respect to the reactants, to proceed to final reaction products. Many radical – molecule reactions relate to this third case as, for instance, the title reaction.⁹ At temperatures above 210 K, a positive temperature dependence of the rate coefficient k(T), i.e. an Arrhenius behavior was observed,¹⁰ and the hydromethoxy (CH₂OH) radical is the main reaction product (T>400 K).¹¹

$${\text{CH}}_3\text{OH}+\cdot \text{OH}\to \cdot {\text{CH}}_2\text{OH}+{\text{H}}_2\text{O}$$ (R1)

At lower temperatures, there is a handful of available experimental rate coefficients especially at temperatures corresponding to interstellar molecular clouds (<100 K)^12–14 and methoxy radicals (CH₃O) have been proposed to be the major reaction product:¹⁴

$${\text{CH}}_3\text{OH}+\cdot \text{OH}\to \cdot {\text{CH}}_3\text{O}+{\text{H}}_2\text{O}$$ (R2)

Despite the presence of an activation barrier, the rate coefficients for the title reaction at temperatures between 22 and 88 K are almost two orders of magnitude larger than the one at ~200 K and a sharp negative temperature dependence of the rate coefficient was observed between 120 and 200 K.^13,14 This enhancement in OH-reactivity was explained by the formation of a weakly bound H-bonded pre-reactive complex, sufficiently long-lived to undergo quantum-mechanical tunneling to form the final products.¹⁴ From an astrochemical point of view, it is worth noting that weakly bound complexes cannot be stabilized through three-body collisions in the gas phase of the ISM environment, opposite to the laboratory, due to low densities in the clouds (10³ – 10⁶ cm^-3 for dense objects) and the most probable stabilization mechanism is radiative association. A number of unsuccessful attempts to detect weakly bound complexes in the ISM and theoretical calculations of the rate coefficients for radiative association showed that large molecules or strong bonding are necessary to obtain relatively high rates.¹⁵ The experimental detection of the CH₃O radical at 80 K by Shannon et al.¹⁴ was a direct evidence that the bimolecular channel was open notwithstanding the presence of a positive activation barrier. Tunneling via the pre-reactive weakly bound complex was postulated to explain these observations and this mechanism is now thought to be extendable to other radical-molecule reactions of class (iii), especially to the oxidation of organic molecules by OH.¹⁶

To support their experimental finding, Shannon et al.¹⁴ calculated the total rate coefficient k(T) for the CH₃OH+OH reaction based on the potential energy surface by Xu and Lin⁹ using a chemical master equation combined with the Eckart approximation for the transmission coefficient for tunneling. They were able to reproduce the negative temperature dependence of k(T) in the temperature range 60 – 250 K. Nevertheless, the predicted T-dependence was found to be less pronounced below 200 K than that observed experimentally and the calculated rate coefficients were about a factor of 5-10 below their low temperature measurements (60-80 K). Later, Siebrand et al.¹⁷ performed new calculations of the potential energy surface (PES), using reaction dynamics and tunneling probabilities to determine k(T) by combining quasi classical trajectory (QCT) method and RRKM theory. Although these authors also found a negative temperature dependence of the rate coefficient below 200 K, it was about a factor of 4 smaller than that obtained by Shannon et al.¹⁴ at ca. 60 K and, hence, more than 20 times below the experiments. Siebrand et al.¹⁷ suggested that Shannon et al.'s results could be theoretically reproduced provided that methanol dimers, (CH₃OH)₂, were present in the experiments and that the reaction of OH with (CH₃OH)₂, which they calculated to be much faster than the reaction with the monomer, was the main contribution to the observed OH loss even at low methanol concentrations. This was questioned by Shannon et al.,¹⁸ who showed that dimerization of methanol was not efficient enough to generate significant amounts of dimers at the low temperature conditions of the experiments. In 2018, Gao et al.¹⁹ published a theoretical investigation concentrating on the possible pressure dependence of the title reaction. They focused on the two limiting situations: the low-pressure limit (LPL), for which the reaction can be considered as a direct H-abstraction process without any stabilized pre-reactive complex formed, and the high-pressure limit (HPL) of k(T) which assumes that the pre-reactive complex is fully stabilized with a population of energy states following a Boltzmann distribution. Rate coefficients were computed between 30 K and 2000 K using the competitive canonical unified statistical (CCUS) model.²⁰ Gao et al.¹⁹ showed that the low temperature experiments (T < 100 K)^12–14 are close to the HPL conditions, but lower by a factor of 2 to 4, hence suggesting–a pressure dependence of k(T).

Subsequently, Roncero et al.²¹ developed a new full dimensional PES used in the QCT calculations on the dynamics of the OH + CH₃OH reaction. This PES accurately describes the long-range interaction and the intrinsic reaction coordinate (IRC) for the two products of the reaction: CH₂OH and CH₃O radicals. The total reaction rate coefficient, calculated between 20 K and 300 K, was found to be almost temperature independent and much lower than the experimental values, especially below 100 K.

Beside the very peculiar behavior of the temperature dependence of the rate coefficient of the title reaction, the second major issue of the work from Shannon et al.¹⁴ was the detection of CH₃O and their theoretical prediction that the branching ratio of reactions (R1) and (R2) should dramatically change with temperature, making CH₃O + H₂O the only exit pathway at interstellar temperatures.

As it can be understood from the preceding description of the state of the art, the title reaction is still a matter of debate and further investigations are certainly desirable. In the present study, we have extended the kinetic measurements down to 11.7 K by using the CRESU (French acronym for Cinétique de Réaction en Ecoulement Supersonique Uniforme or Reaction Kinetics in a Uniform Supersonic Flow) machine available in Ciudad Real, which is coupled to laser techniques for the production of OH radicals by pulsed laser photolysis (PLP) and for their detection by laser induced fluorescence (LIF). The lowest temperature presently achievable with our apparatus is the lowest one obtained with a pulsed CRESU worldwide ever. In this work, we present an extensive series of total rate coefficient measurements in the temperature range 11.7 – 177.5 K and testing for the pressure dependence at different temperatures than those explored by Shannon et al.¹⁴.

In addition to the experiments, the high- and low-pressure rate coefficients k(T) were also studied in detail using high-level quantum chemical and theoretical kinetic methodologies, closely reproducing the experimental data between 20 and 390 K. Branching ratios for CH₃O and CH₂OH formation are also evaluated and compared to previous estimations. The kinetic model in those calculations, shown in Scheme 1, reflects the current understanding of the mechanism of the reaction discussed above, i.e. a case (iii) reaction with an intermediate complex that has access to redissociation and two H-abstraction channels.

Scheme 1.

Reaction scheme considered in the kinetic model.

2. Experimental part

The details and ideas on the CRESU technique and its application to astrochemistry can be found elsewhere.^22–29 The technique is based on a uniform supersonic expansion of gas from a reservoir through a Laval nozzle into a vacuum chamber. Compared to continuous CRESU as originally developed, the pulsed CRESU technique used in a number of laboratories including Ciudad Real allows obtaining low temperatures and sufficiently long lengths of expansion uniformity at much smaller pumping. The description of the pulsed and continuous CRESU apparatus used in this work and the operational procedure developed in our group are given in previous publications.^30–34 Hence, we only describe here the specificities and novelties of the present study.

2.1. Characterization of the Jet Temperature (T) and Gas Density (n)

To extend the temperature range covered in previous investigations (21 – 107 K), down to about 10 K and up to about 200 K, two new Laval nozzles were constructed and aerodynamically characterized by measuring the impact pressure as a function of the distance from the exit of the Laval nozzle, using the standard Pitot tube technique. The procedure to determine the temperature and gas density in the supersonic jet for the new Laval nozzles employed is explained in the Supplementary Information.

The two nozzles, denoted as He-15K and Ar-100K, were initially designed to operate with helium at 15 K and argon at 100 K, respectively. As explained by Canosa et al.,³⁴ one geometrical Laval contour can be used for many flow conditions and different buffer gases although temperature T and pressure P in the flow cannot be chosen independently. In the present situation, it was observed that increasing the helium mass flow rate compared to that used for the original He-15K profile leads to supersonic flows having a longer uniformity and fewer flow fluctuations. Several (T, P) flow conditions were then obtained with a temperature somewhat lower than the theoretical 15 K. The lowest temperature achievable was (11.7 ± 0.7 K), with a length of uniformity d_max of 53 cm, making this flow the coldest pulsed CRESU flow ever generated worldwide. The Ar-100 K nozzle was also validated for a series of different argon mass flow rates, providing an accessible temperature range of 89 – 123 K. Nitrogen, instead of argon, was used as well with this nozzle at different mass flow rates, allowing us to explore the 135 – 178 K temperature range with a highest temperature achievable of (177.5±1.2 K), getting a uniform flow along 9 cm. The uniformity length ranges from 9 to 29 cm for the Ar-100K nozzle conditions, which corresponds to hydrodynamic times between 181 and 646 μs. For the He-15K nozzle, d_max ranges from 32 to 53 cm with hydrodynamic times between 186 and 443 μs. The operating conditions employed for the He-15K and Ar-100K nozzles and spatial profiles of their expansion temperatures can be found in Tables S1 and S2 and Figs. S1 and S2 of the Supplementary Information.

Additionally to the Pitot measurements, the conventional pulsed laser photolysis-laser induced fluorescence (PLP-LIF) technique was used for recording the “ultra-cold” LIF spectrum of OH radicals between 281.0 and 282.8 nm with a spectral resolution of 0.002 nm or 0.004 nm at a fixed delay time between the photolysis and excitation lasers (40 μs). An example of the recorded LIF spectrum at 11.7 K is presented in Fig. S3 of the Supplementary Information. Even though the OH radical is not a perfect “thermometer” for getting the jet temperature, there is a good agreement of the experimental LIF spectrum with the simulated one, corroborating the results of the Pitot tube measurement.

2.2. Kinetic Measurements

The PLP-LIF technique has been intensively employed in our laboratory in Ciudad Real for kinetic studies on gas-phase reactions between radical species and atmospheric pollutants, as previously described.^35–38 Therefore, only a brief description is given here.

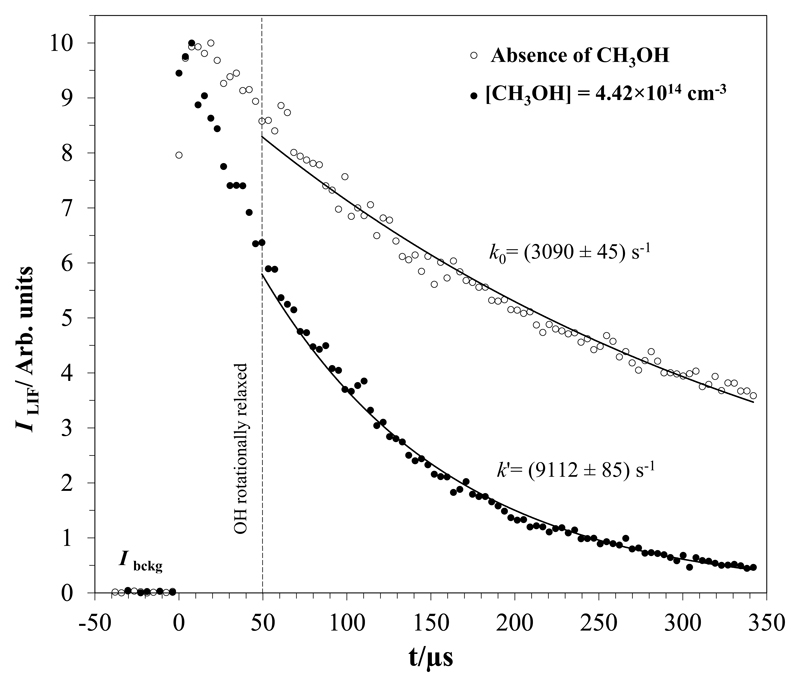
OH radicals were generated in situ in the jet by UV photolysis of the molecular precursor (H₂O₂ or t-BuOOH) at 248 nm. The output laser energy was around 10 mJ pulse^-1 at 10 Hz. The evolution of the LIF signal (I_LIF) from OH radicals in the course of the reaction with CH₃OH and/or OH-precursor was monitored at ca. 310 nm, after laser excitation OH at 282 nm (less than 1.0 mJ pulse^-1 at 10 Hz, measured at the exit of the doubling unit of the laser). An example of the temporal profile of I_LIF at 122.5 K, with and without methanol in the gas mixture, is shown in Fig. 1. The initial rise of the LIF signal corresponds to the population of OH (X²Π, v″=0) after rotational relaxation (timescale of a few tens of μs).

Fig. 1.

Example of the temporal profiles of the OH LIF signal recorded at 122.5 K.

The kinetic experiments were performed under pseudo-first order conditions, i.e. in a large excess of methanol and OH-precursor with respect to initial OH concentration. Under these conditions and after the rotational relaxation, the LIF signal of OH radicals exhibit an exponential decay:

$${\text{I}}_{\text{LIF}}\left(\text{t}\right)={\text{I}}_{\text{LIF}}(\text{t}=0)\text{exp}(-k^{\prime }t)$$ (E1)

At a constant jet temperature, the pseudo-first order rate coefficient, k′, is then given by

$$k^{,}=k(\text{T})[{\text{CH}}_3\text{OH}]+k_0$$ (E2)

where k(T) is the total removal rate coefficient for the OH+CH₃OH reaction (obtained from k′ vs [CH₃OH] plots) and k₀ is the pseudo-first order rate coefficient in the absence of methanol, covering all other losses of OH. In order to compare the kinetic results obtained at different temperatures, where k₀ can vary significantly, k′ was corrected with k₀ for every single experiment converting eqn (E2) into eqn (E3).

$$k^{\prime }-k_0=k(\text{T})[{\text{CH}}_3\text{OH}]$$ (E3)

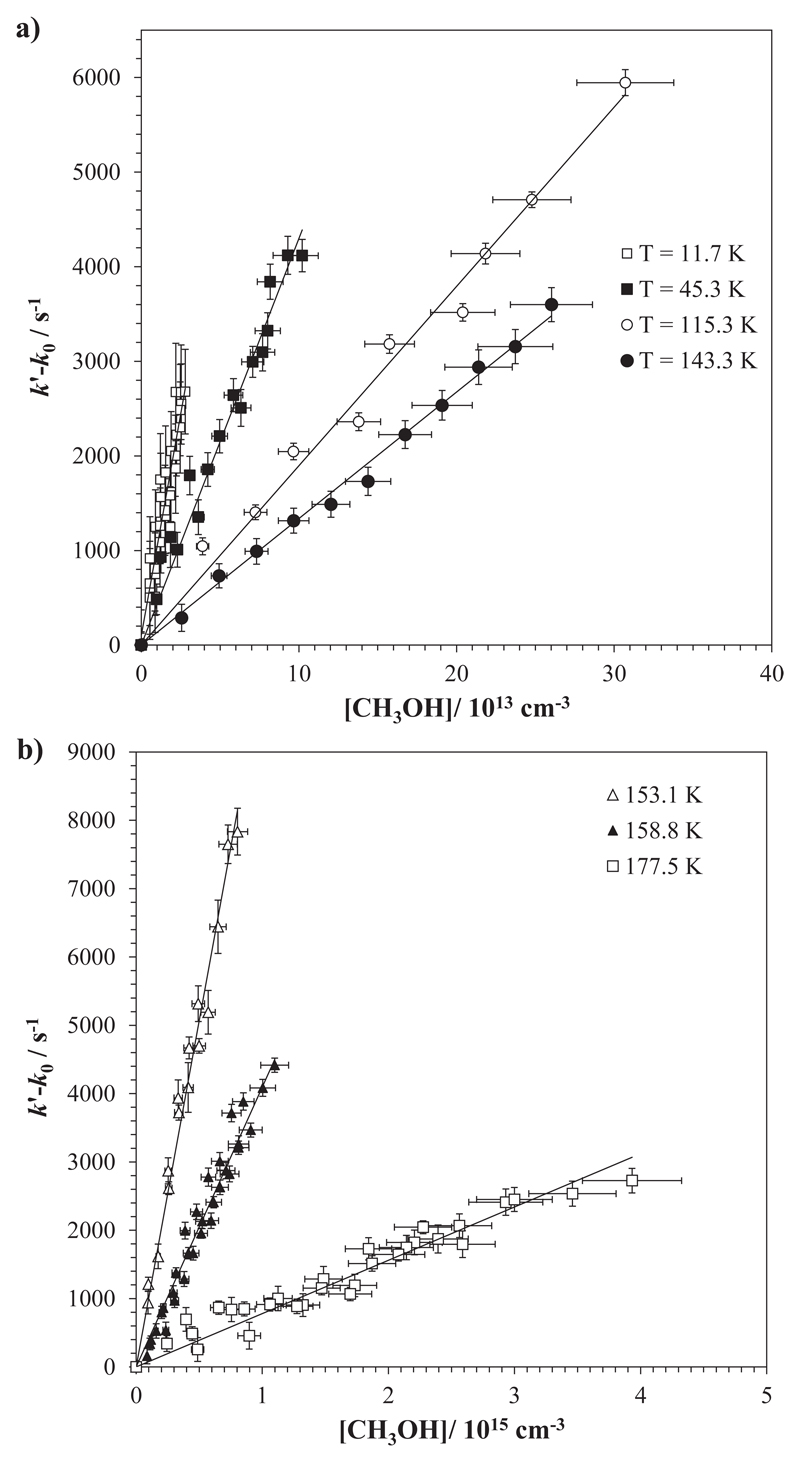
It is worth noting here that eqn (E2) and eqn (E3) are only correct for low methanol concentrations; at high methanol concentrations, deviation of k' from linearity (downward curvature) due to methanol clustering has already been observed and already been discussed elsewhere.^12–14,18 The rate coefficients k(T) were then obtained from k′-k₀ versus [CH₃OH] plots in the concentration range where the bimolecular plots were linear (see Fig. 2).

Fig. 2.

Examples of the bimolecular plots according to eqn (E3) for selected temperatures. Uncertainties in methanol concentration are conservatively considered as ±10%, while for k′ and k₀ the error bars are standard deviation obtained from the fit of the OH decay to eqn (E1).

The concentration of methanol in the jet was calculated from the total gas density (n) obtained from the Pitot tube measurements (see Supplementary Information) and the proportion of methanol in the jet:

$$[{\text{CH}}_3\text{OH}]=\frac{F_{\text{methanol/buffer}}}{F_{\text{Total}}}\times f\times n$$ (E4)

F_{methanol/buffer} is the calibrated mass flow rate through the reservoir for diluted methanol (f, dilution factor) and F_Total is the total mass flow rate (i.e. sum of the main flow of buffer gas, the buffer gas flow through the glass bubbler containing H₂O₂ or t-BuOOH, and F_{methanol/buffer}).

Table S3 of the SI lists the methanol concentrations calculated from eqn (E4). As [CH₃OH] has to be accurately known to derive a reliable rate coefficient and depends on the dilution factor in the bulb, f, this parameter was periodically checked by UV absorption spectroscopy at 185 nm, as explained in the Supplementary Information. The optical measurements were carried out at room temperature as described by Ocaña et al.³¹ [CH₃OH] values from flow measurements typically differ less than 5% with respect to those from the UV spectroscopic measurements.

2.3. Reagents

Buffer gases He (99.999%, Praxair), N₂ (99.999%, Praxair) and Ar (99.999%, Praxair) were used as supplied. A liquid sample of methanol (99.8%, Sigma-Aldrich) was placed in a thermalized flask (V = 250 mL) and degassed by repeated freeze-pump-thaw cycles prior to use. An aqueous solution of H₂O₂ (Sigma-Aldrich, initially at 50% w/v) was pre-concentrated as described earlier (Jiménez et al. 2005a, 2005b), while (CH₃)₃COOH (70% t-BuOOH, Sigma-Aldrich) was used without pre-concentration, since its vapor pressure is higher than that of water. The bubbler containing (CH₃)₃COOH was placed in a water/ice bath at 7-9 °C to reduce the t-BuOOH vapor pressure.

3. Theoretical part

3.1. Quantum Chemical Methodology

The critical points on the CH₃OH + OH potential energy surface, i.e. the reactants, pre-reaction complex, H-abstraction transition states, and products were characterized by geometry optimization at the M06-2X/aug-cc-pVQZ level of theory.^39,40 Transition states (TSs hereafter) were verified by IRC calculations at the same level of theory, using a step size of 0.05 Bohr. An IRCMax geometry⁴¹ was then located for the TSs along these IRC paths, searching the geometry with the highest CCSD(T)/aug-cc-pVTZ potential energy.^39,42 For all geometries (IRCMax geometries for the TSs), single point energies were calculated at the CCSD(T)/aug-cc-pVxZ (x = D, T, Q) levels of theory, with an extrapolation to the complete basis set (CBS) limit using the aug-Schwartz6 (DTQ) scheme by Martin.⁴³ The uncertainty of this methodology is expected to be of the order of ~0.5 kcal mol^-1. The energy profiles of the TS IRC pathways were further improved by single-point CCSD(T)/aug-cc-pVTZ calculations at intervals of ~0.15 Bohr. The reaction of CH₃OH with OH, a barrierless channel forming the pre-reaction complex, was characterized by constrained geometry optimizations at the M06-2X/aug-cc-pVQZ level of theory, for pre-set distances of the reactants ranging from 4 to 9.5 Å, and the energy profile of this complexation pathway was improved using single-point CCSD(T)/aug-cc-pVTZ calculations. Smooth interpolation of the rovibrational and energetic characteristics by C-splines then provides a continuous description along the reaction coordinate. Additional calculations were performed on B3LYP-D3/aug-cc-pVQZ and ωB97XD/aug-cc-pVQZ geometries,^44–47 but these were not found to be of better quality and are thus not used in the present work. The Supplementary Information (Table S7) tabulates the relative energies obtained in this work and those available in the literature.

The quantum chemical calculations were performed using Gaussian-16.⁴⁸

3.2. Theoretical Kinetics Methodology

The CH₃OH+OH reaction is modelled as a two-step reaction, with an initial complexation reaction (k_a), followed by a subsequent reaction of the pre-reaction complex, being either a redissociation to the free reactants (k_-a), or H-abstraction from either the methyl group (k_b1) or the hydroxy group (k_b2), as schematized in the introduction.

The high-pressure rate coefficients k_b1(T) and k_b2(T) for reaction over a saddle point were calculated using multi-conformer canonical transition state theory (MC-CTST) in a rigid rotor harmonic oscillator (RRHO) approximation⁴⁹ using the M06-2X/aug-cc-pVQZ rovibrational characteristics and the (IRCMax) CCSD(T)/CBS(DTQ)//M06-2X energies, augmented with conformer-specific zero-curvature WKB tunneling corrections⁵⁰ based on the CCSD(T)/aug-cc-pVTZ//M06-2X IRC energy profiles. The rate coefficient k_a(T) of the CH₃OH+OH complex formation is based on E,J-resolved micro-variational transition state theory calculations (E,J-μVTST) in an RRHO approximation.⁵¹ At higher internal energies, i.e. relevant at 100-300 K, the kinetic bottleneck is positioned well towards the complex (e.g. a separation of ~5.5 Å for the energies relevant at 300K), and the RRHO approximation is expected to work reasonably well. For the lowest energies in the CH₃OH+OH reactants, however, the kinetic bottleneck is positioned at larger separations, where relative motion of CH₃OH and OH constitutes nearly unhindered translations and relative rotations. Here, the predicted rate coefficients are critically dependent on the description of the transitional modes. At the lowest temperatures, ≤ 100 K, we thus expect a larger uncertainty for our rate predictions than at higher T, most likely resulting in an underestimate of k_a(T) and k_-a(T). At temperatures above 400 K, vibrational anharmonicities and internal rotations will start to play a larger role in the calculation of the entropy, and care should be taken when extrapolating the current results to temperatures prevalent in e.g. combustion systems. In the TST calculations, the complex is assumed to be in the HPL (i.e. to have a Boltzmann energy distribution); the validity of this assumption is discussed in detail later. The overall rate coefficient for effective product formation, k_HPL(T), is then derived from the TST rate coefficients of the elementary reaction as shown in eqn (E5).

$$k_{HPL}(T)=k_a(T)\frac{k_{b1}(T)+k_{b2}(T)}{k_{b1}(T)+k_{b2}(T)+k_{-a}(T)}$$ (E5)

The product yield Y_j(T) for product j (=1 for CH₂OH and 2 for CH₃O) is then given by the ratio Y_j(T) = k_bj(T)/{k_b1(T)+k_b2(T)}.

The energy-specific rate coefficients, k_b1(E) and k_b2(E), for H-abstraction were calculated using RRKM theory in an RRHO approximation, corrected by WKB zero-curvature tunneling. Energy-specific rates k_-a(E) of complex redissociation were obtained from the E,J-μVTST k_a(T) rate coefficient by inverse Laplace transformation (ILT) to ensure consistency. The RRKM calculations are energy-specific and are used for the treatment of the LPL, where the complex energy is determined by the nascent energy distribution F_T(E) above the dissociation energy, E_diss, from the initiation complexation reaction at the temperature considered. The overall rate coefficient for effective product formation k_LPL(T) is then derived from the energy-specific rate coefficients of the elementary reactions as shown in eqn (E6).

$$k_{LPL}(T)=k_a(T){\displaystyle {\int }_{E=E_{diss}}^{\infty }{F}_T(E)\frac{k_{b1}(E)+k_{b2}(E)}{k_{b1}(E)+k_{b2}(E)+k_{-a}(E)}dE}$$ (E6)

with E the internal energy of the prereaction complex, and with F_T(E) the formation probability⁵² of the complex for reactants with a canonical energy distribution:

$$F_T(E)=\frac{1}{N}{G}_a^{\ne }(E)\mathit{\text{exp}}\left(\frac{-E}{kT}\right)$$ (E7)

where N is the probability normalization factor, and G^≠_a(E) the energy-specific sum of states for the barrierless complexation reaction a.

The product yield Y_j(T) is then given by the following expression:

$$Y_j(T)={\displaystyle {\int }_{E=E_{diss}}^{\infty }{F}_T(E)\frac{k_{bj}(E)}{k_{b1}(E)+k_{b2}(E)}dE}$$ (E8)

In order to compare the k_x(E) (with x= -a, b1 or b2) with the collision frequencies for the pre-reaction complex (estimated parameters σ_AA = 4.5 Å, ε_AA = 350 K) at specific (T,P) conditions, including atmospheric ones, these were calculated from the Lennard-Jones collision number, using N₂ as a collision partner (σ_AA = 3.62 Å, ε_AA = 97 K). The kinetic calculations were executed using modules of our in-house software.⁵²

4. Experimental results and discussion

4.1. Temperature Dependence of k(T) between 11.7 K and 177.5 K: CRESU Experiments

The rate coefficients k(T) for the OH + CH₃OH reaction obtained in this work below and above 100 K are presented in Tables 1 and 2, respectively, and plotted in Fig. 3 (blue circles). Uncertainties in Fig. 3 represent the total error (statistical (±2σ) and systematic errors). Based on the typical differences (<5%) between the mass flow and optical measurements of the methanol concentration, a conservative 10% systematic error has been assigned to take into account inaccuracies or miscalibrations of instruments such as mass flow controllers or pressure gauges, which directly affect the determination of the methanol concentration. In Tables 1 and 2, k(T) previously reported in the literature by Gómez-Martín et al.,¹³ Shannon et al.¹⁴ and Antiñolo et al.¹² have also been included for comparison purposes.

Table 1.

Experimental gas-phase rate coefficients for the OH+CH₃OH reaction obtained in this work together with those from previous studies at T<100 K. Uncertainties ±σ reported here for this work are only statistical.

ca. T/ K	T/ K	Bath Gas	n / 1016 molecule cm-3	k(T)/ 10-11 cm3molecule-1 s-1	Reference
	11.7 ± 0.7	He	6.88 ± 0.62	9.38 ± 0.64	This work
	13.0 ± 0.7	He	6.41 ± 0.55	7.77 ± 0.36	This work
	14.3 ± 0.8	He	5.90 ± 0.52	8.78 ± 0.37	This work
	22.1 ± 1.4	He/N2	1.91 ± 0.25	5.57 ± 0.71	This work
	21.1 ± 0.6	He	3.37 ± 0.15	6.05 ± 0.22	This work
~ 22	22.5 ± 0.7	He	7.43 ± 0.32	6.19 ± 0.17	This work
	21.7 ± 1.4	He	16.7 ± 1.60	9.05 ± 0.41	This work
	22.4 ± 1.4	He	16.7 ± 1.60	4.30 ± 0.66	Antiñolo et al.12
	36.2 ± 1.2	He	17.73 ± 0.86	5.92 ± 0.29	This work
	42.5 ± 1.3	He/N2*	5.22 ± 0.33	2.74 ± 0.42	Antiñolo et al.12
~ 45	47.7 ± 0.6	N2*	2.74 ± 0.09	2.17 ± 0.35	Antiñolo et al.12
	45.3 ± 1.3	He/N2	4.23 ± 0.28	4.08 ± 0.19	This work
	50.5 ± 1.4	N2	1.50 ± 0.12	2.70 ± 0.11	This work
	51.6 ± 1.7	N2*	4.17 ± 0.35	2.47 ± 0.15	This work
~ 50	51.6 ± 1.7	N2*	4.17 ± 0.35	2.19 ± 0.26	Antiñolo et al.12
	52.2 ± 0.9	Ar*	5.15 ± 0.13	2.97 ± 0.60	Antiñolo et al.12
	49.9 ± 1.4	He/N2	8.33 ± 0.41	3.30 ± 0.19	This work
	52.1 ± 0.5	Ar	19.52 ± 0.28	2.93 ± 0.24	This work
	56.0 ± 4.0	Ar	4.4 ± 0.5	4.9 ± 0.8	Gómez Martín et al.13
	61.0 ± 1.0	N2*	2.02 ± 0.08	2.11 ± 0.75	Antiñolo et al.12
	64.2 ± 1.7	N2*	2.24 ± 0.15	1.47 ± 0.23	Antiñolo et al.12
~ 64	63.0 ± 4.0	N2	3 ± 1	4.2 ± 0.4	Shannon et al.14
	64.1 ± 1.6	He/N2	4.63 ± 0.27	2.91 ± 0.10	This work
~ 70	69.5 ± 1.6	N2	3.26 ± 0.19	4.77 ± 0.21	This work
	68.8 ± 0.6	Ar/N2	16.58 ± 0.27	5.58 ± 0.32	This work
	82.0 ± 4.0	N2	5.1 ± 0.7	3.4 ± 0.5	Shannon et al.14
~ 80	81.0 ± 4.0	N2	8.9 ± 1.0	3.2 ± 0.5	Shannon et al.14
	79.0 ± 4.0	N2	17 ± 2	3.3 ± 0.6	Shannon et al.14
	88.0 ± 8.0	Ar	9.4 ± 1.3	3.8 ± 0.4	Gómez Martín et al.13
~ 90	89.5 ± 0.6	N2	18.24 ± 0.33	4.83 ± 0.12	This work
	89.1 ± 0.7	Ar	43.4 ± 0.51	4.30 ± 0.22	This work

^*continuous flow conditions

Table 2.

Experimental gas-phase rate coefficients for the OH+CH₃OH reaction obtained in this work together with those from previous studies at T=100-200 K. Uncertainties ±σ reported here for this work are only statistical.

ca. T./ K	T/ K	Bath Gas	n / 1016 molecule cm-3	k(T)/ 10-11 cm3molecule-1 s-1	Reference
~ 100	99.3 ± 0.4	N2	7.67 ± 0.09	4.76 ± 0.05	This work
	101.8 ± 0.6	Ar	18.34 ± 0.17	3.74 ± 0.08	This work
~ 107	107.0 ± 0.5	N2	4.90 ± 0.06	2.03 ± 0.02	This work
	106.0 ± 0.6	Ar	14.02 ± 0.11	2.15 ± 0.07	This work
	115.3 ± 1.1	Ar	9.58 ± 0.14	1.85 ± 0.07	This work
~ 123	123 ± 5*	He	3.15 ± 0.15	0.43 ± 0.21	Gómez-Martín et al.13
	122.5 ± 1.0	Ar	7.20 ± 0.08	1.21 ± 0.04	This work
	130 ± 5*	He	6.6 ± 0.3	0.39 ± 0.21	Gómez-Martín et al.13
~ 137	138 ± 9	N2	7.8 ± 1.0	0.53 ± 0.17	Gómez-Martín et al.13
	136.1 ± 0.8	N2	24.92 ± 0.35	1.83 ± 0.08	This work
	140.4 ± 1.0	N2	21.68 ± 0.40	1.24 ± 0.03	This work
~ 143	143 ± 5*	He	2.76 ± 0.14	0.31 ± 0.12	Gómez-Martín et al.13
	143.3 ± 0.6	N2	17.02 ± 0.17	1.36 ± 0.03	This work
~150	153.1 ± 0.7	N2	9.14 ± 0.11	0.98 ± 0.04	This work
	149.9 ± 0.7	N2	10.69 ± 0.12	1.28 ± 0.10	This work
	148.3 ± 0.6	N2	12.35 ± 0.13	1.84 ± 0.04	This work
	158.8 ± 0.6	N2	7.40 ± 0.07	0.43 ± 0.02	This work
~ 165	163 ± 5*	He	2.46 ± 0.13	0.17 ± 0.07	Gómez-Martín et al.13
	165.7 ± 0.9	N2	5.64 ± 0.08	0.17 ± 0.01	This work
	177.5 ± 1.2	N2	6.71 ± 0.11	0.071 ± 0.003	This work
	180 ± 10*	He	1.59 ± 0.08	0.07 ± 0.02	Gómez-Martín et al.13
	202 ± 2*	He	1.30 ± 0.06	0.060 ± 0.008	Gómez-Martín et al.13

^*Flow tube technique

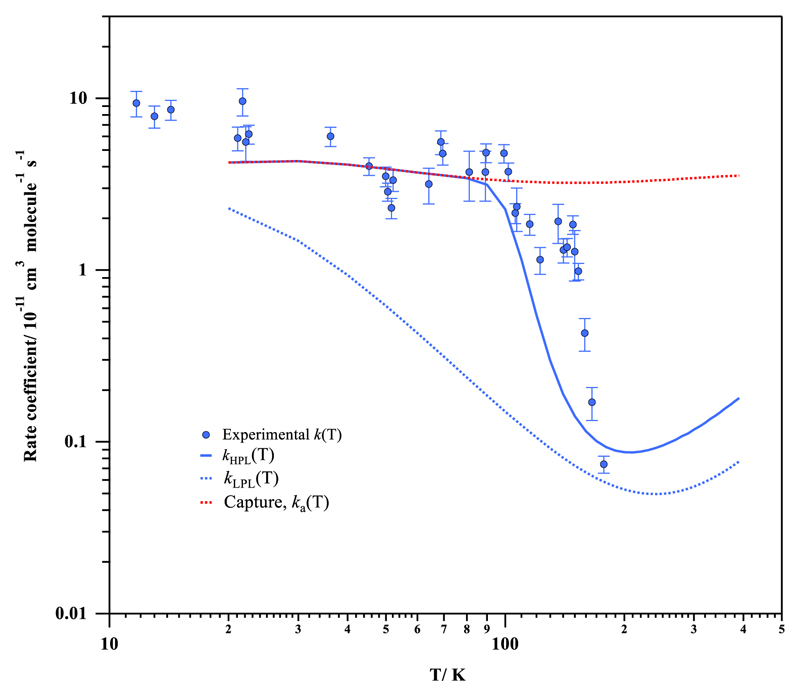
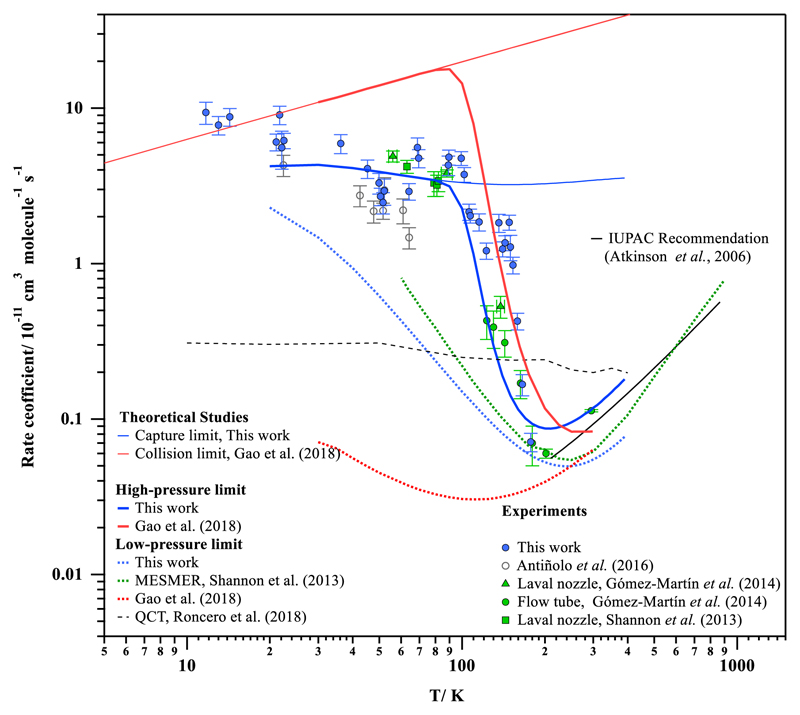
Fig. 3.

Experimental and theoretical rate coefficients for the reaction of OH with CH₃OH as a function of temperature between 11.7 K and 390 K.

We observe a large increase in k(T) from 177.5 K to 99.3 K (k(177.5 K)/ k(99.3 K) ~ 65) qualitatively in agreement with the previous study by Gómez Martín et al.,¹³ while the increase of k(T) between 99.3 K and 11.7 K is less dramatic (k(11.7 K)/ k(99.3 K) ~ 2). With respect to k(300 K), the enhancement of the OH-reactivity for methanol is around two orders of magnitude at 11.7 K, while at 100 K k(T) increases more than one order of magnitude. The present results confirm the general trend observed by Gómez Martín et al.¹³ and clarify the temperature dependence at temperatures below 100 K for which it remains negative albeit much weaker than in the 100 – 200 K range. Eventually, at the lowest temperatures explored (T < 20 K) asymptotic behavior of the rate coefficient can be apparent.

4.2. k(T) as a Function Total Gas Density (Pressure)

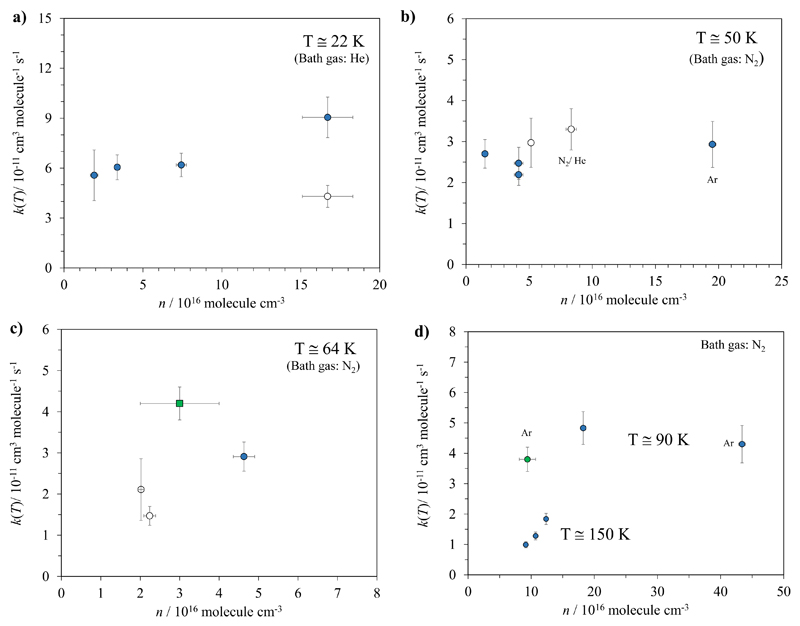
In Tables 1 and 2, the experimental kinetic data reported here and those from the literature have been joined by similar temperatures (first columns) and by increasing gas densities (4^th column) in order to evaluate if a dependence of k(T) with total pressure is detectable. Figure 4 displays the rate coefficient as a function of gas density for 22 K, 50 K, 64 K, 90 K and 150 K. As shown in Fig. 4a, k(22 K) increases at the largest gas density with respect to n lower than 7.4×10¹⁶ cm^-3. Considering the overlap of error bars for these four different experiments, a possible pressure dependence is difficult to ascertain, however. The value of k(22 K) reported by Antiñolo et al.¹² has been included as well in Fig. 4a. The results obtained by Antiñolo et al.¹² are globally lower than the global trend reported here. However, the major discrepancy appears at 22 K and 64 K (around twice). A combination of several potential sources of error could explain this discrepancy. At 22 K, in this work the laser excitation energy is higher and the methanol concentration range is shorter, i.e. the OH LIF signals are of better quality and the influence of methanol dimerization and, therefore, curvature of the k’-k₀ vs. [CH₃OH] plots is reduced. At 64 K, the Laval nozzles employed by Antiñolo et al.¹² and in this work are different. In the present study, the hydrodynamic time was more than three times larger than the one available in the previous study. This allowed us to scan LIF decay signals over several OH lifetimes thus improving the accuracy of k' determinations with respect to those obtained by Antiñolo et al.¹² At 50 K, our results and the kinetic data from Antiñolo et al.¹² are combined in Fig. 4b, demonstrating the absence of pressure dependence of k(50 K) within a quite large density range: (1.5 - 19.5)×10¹⁶ cm^-3, independently of the nature of the bath gas (N₂, Ar or He) within the error bars. The same conclusion can be derived at 64 K and 90 K (Fig. 4c-d). Finally, the three measurements carried out at about 150 K (Fig. 4d) do show a pressure dependence within a rather limited density range.

Fig. 4.

Rate coefficients for the OH+CH₃OH reaction as a function of the gas density between 22 K and 150 K. Legend: ● This work; ○ Antiñolo et al.¹²; ■ Shannon et al.¹⁴ and ● Gómez-Martín et al.¹³

As shown in Tables 1 and 2, other temperatures have been explored but rate coefficients were obtained for only two different densities at around 70 K, 100 K and 107 K. No density effect was observed for these temperatures within the error bars. At higher temperatures (excepting 150 K) only one measurement was made for temperatures ranging from 120 K to 180 K. Nevertheless, several temperatures coincide with those explored by Gómez-Martín et al.,¹³ allowing for comparison. At 123, 137 and 143 K our k(T) measurements are about 3-4 times higher than those of Gómez-Martín et al.¹³ (a factor 2.8, 3.5 and 4.4 respectively), whereas our gas density is also higher (by factors 2.3, 3.2 and 6.2 respectively). At the highest temperatures (165 and 180 K) however, our kinetic data and those from the Leeds group coincide perfectly although gas densities are quite different (see Table 2). How can we reconcile these observations? The Leeds experiments at 123, 143, 163 and 180 K have been carried out using a cryogenically cooled flow tube reactor, whereas the measurement at 138 K was realized in their CRESU machine. Condensation onto the flow tube walls is one of the well-known drawbacks of the technique and becomes more critical at the lowest temperatures. A loss of methanol at the walls would induce an underestimation of the deduced rate coefficient which qualitatively agrees with the present observation. Nevertheless, this would require a very important loss (about 70%) and one would expect that the discrepancy would increase when the temperature is decreased, opposite to what is observed. Furthermore, this argument cannot hold for the CRESU measurement at 138 K as condensation is inhibited in this wall-free reactor. The Leeds experiments present much larger uncertainties in the temperature determination than in our apparatus. As the discrepancy occurs in the temperature domain where the rate coefficient rises very sharply, we have made a rough estimation of how sensitive the rate coefficient is to a temperature change by 5 K, finding a deviation of typically 40% around 140 K, too small to explain the observed difference. Anticipating the theoretical discussion, it can be mentioned that the predicted k_HPL/k_LPL ratio increased from about 1.6 at 180 K up to 5.2 at 120 K, indicating a larger pressure dependence at the latter temperature. This could qualitatively explain why no pressure dependence is observed at T ≥ 165 K, whereas rate coefficients change with density at lower temperatures. Finally, it can be noted that the k_HPL/k_LPL ratio prediction reaches a maximum at around 90 K (see Fig. 3) where one should then expect a significant pressure dependence of k(T). As commented previously, this is not the case at 90 K (Fig. 4d) which may indicate that the reaction is in the HPL regime at this temperature.

5. Theoretical results and discussion

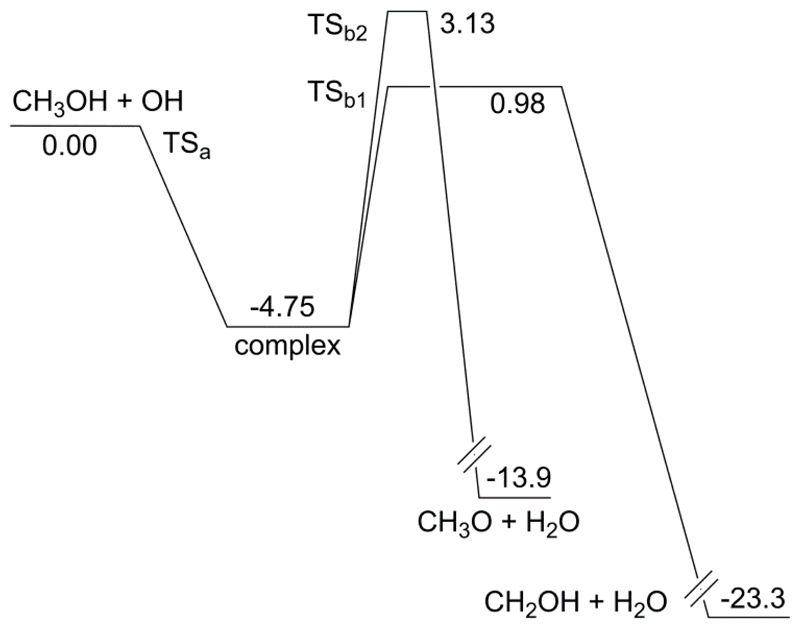
Table 3 shows the relative energy of all critical points on the CH₃OH+OH PES, shown also in Fig. 5.

Table 3.

Relative energies (kcal mol^-1) of the critical points on the CH₃OH + OH potential energy surface. The geometry optimizations are at the M06-2X/aug-cc-pVQZ level of theory, indicated in the second column. The remaining column headers indicate the basis set size for single-point CCSD(T) calculations. Additional energetic data are available in Table S7.

Species	M06-2X	aug-cc-pVDZ	aug-cc-pVTZ	aug-cc-pVQZ	CBS(DTQ)
CH3OH + OH	0.00	0.00	0.00	0.00	0.00
Complex	-4.96	-4.93	-5.00	-4.87	-4.75
TSb1	0.23	0.87 1.01 a	0.92 1.11 a	0.87 1.04 a	0.82 0.98 a
TSb2	0.94	3.13 3.31 a	2.56 2.71 a	2.74 2.91 a	2.94 3.13 a
CH2OH + H2O	-22.67	-20.15	-21.55	-22.51	-23.28
CH3O + H2O	-14.33	-13.13	-13.44	-13.70	-13.91

^(a)IRCMax geometry selected on the highest CCSD(T)/aug-cc-pVTZ energy along the DFT IRC pathway.

Fig. 5.

Potential energy surface (kcal mol^-1) for the CH₃OH + OH reaction at the CCSD(T)/CBS(DTQ)//IRCMax(CCSD(T)/aug-cc-pVTZ//M06-2X/aug-cc-pVQZ) level of theory.

In Table S4 of the SI, the computed rate coefficient for all steps of the reaction mechanism (k_a, k_-a, k_b1 and k_b2) at the HPL are presented in the 20-400 K temperature range together with the yield of reaction products (CH₂OH and CH₃O). In Table S5 of the SI, the same rate coefficients and yields are listed for the low-pressure limit. Additionally, the computed rate coefficients for the complexation reaction (k_a) and the high- and low-pressure limit rate coefficients (k_LPL(T) and k_HPL(T)) are also depicted in Fig. 3.

5.1. Potential Energy Surface

Two energetically accessible transition states geometries were found for abstraction of the H-atom from methyl, in agreement with earlier work by Gao et al.¹⁹. The abstraction of the H-atom from the hydroxyl group likewise has multiple conformers, but only one contributes to the temperatures considered in this work; the other conformers are omitted. For CH₃OH and the pre-reaction complex, only a single optimal structure was used; for OH, a spin-orbit splitting of 27.95 cm^-1 was taken into account.⁵³ The features of the CH₃OH+OH PES have been described in great detail earlier ^9,19 and need not be repeated here; for our current analysis, it is sufficient to recognize the two-step reaction mechanism for effective product formation (CH₂OH or CH₃O + H₂O) through a complex as discussed above.

5.2. High pressure regime: k_HPL(T) and CH₂OH and CH₃O yields

The temperature-dependent kinetics of the CH₃OH + OH reaction at high pressure can be described as three kinetic regimes.

Regime I, T> 230 K: the redissociation of the pre-reaction complex is sufficiently fast to establish a steady-state equilibrium between the complex and the free reactants, with only a few per cent of the complex formed (~5% at 300 K) resulting in effective product formation and the remainder redissociating to the free reactants. This is also shown in Fig. 6, where at high internal energies of the pre-reactive complex, as accessible at these temperatures, the redissociation rate k_-a(E) strongly exceeds the rates for H-abstraction. The lifetime of the complex, despite being collisionally stabilized, is short, <1×10^-9 s at 230 K. The pre-reaction complex has virtually no impact on the kinetics, other than allowing tunneling through a wider range of internal energies than nascently accessible from the reactants, and the reaction behaves as a direct H-abstraction reaction through the two product-forming channels. Tunneling is not overly important, accelerating the overall reaction rate only by a factor of ~2 at 300 K. Our a priori rate predictions in this regime are close to the IUPAC recommendation, ¹⁰ on average within a factor of 1.3 (see Fig. 7); the dominant product is CH₂OH + H₂O, in agreement with the experimental data;¹¹ CH₃O + H₂O is predicted in a ~5% yield at 300 K, at the lower end of the IUPAC¹⁰ recommended 15±10 % range.

Fig. 6.

Energy-specific rate coefficients for the three reaction channels for the pre-reaction complex (redissociation, CH₂OH+H₂O formation, CH₃O+H₂O formation) as a function of the internal energy of the complex, and compared to the collision frequency in two relevant conditions. E_diss = 4.75 kcal mol^-1, E_TSb1 = 5.73 kcal mol^-1 and E_TSb2 = 7.88 kcal mol^-1 (see Fig. 5).

Fig. 7.

Experimental and theoretical rate coefficients for the reaction of OH with CH₃OH as a function of temperature between 11.7 K and 500 K.

Regime II, T< 80 K: Here, the rate limiting step is the complexation reaction, for which we derive a nearly T-independent value (see Fig. 3 and Table S4). In the high-pressure regime, the complex redissociation is negligible and the reaction proceeds through the H-abstraction TS by tunneling, which increases the unimolecular H-abstraction rate coefficients (k_b1 and k_b2) by many orders of magnitude (see Table S4). This is also seen in Fig. 6, where at low internal energies of the complex, redissociation is energetically impossible, such that all association reactions lead to H-abstraction. Interestingly, the dominant product is CH₃O+H₂O at 80 K, despite its higher TS barrier, due to faster tunneling through its narrower energy barrier compared to CH₂OH + H₂O; this change in dominant product compared to room temperature conditions has been reported before,^14,19 and is further illustrated in Fig. 6, showing how k_b2(E) gains on and ultimately surpasses k_b1(E) at the lowest energies. Below 40 K, the tunneling predictions become highly unreliable due to the limitations of the methodology, and no product distribution is proposed in this work for these temperatures. The width of the barrier of the CH₃O+H₂O pathway, however, becomes equal to or even exceeds that of the CH₂OH+H₂O channel at the lowest energies (see Fig. S7). Hence, below 40 K, CH₂OH yield might increase again. More elaborate tunneling corrections using rigorous non-semi-classical multi-dimensional methodologies, or experimental product studies, would be needed to confirm the product distribution. The high-pressure lifetime of the complex is predicted to be less than 1 second at 50 K. Although the predicted total rate coefficient at the lowest temperatures carries a larger uncertainty, it remains within a factor of 1.6 of the experimental data at 20 K.

Regime III, T =80-230 K: here, the reaction transitions between the H-abstraction-controlled and capture-controlled regimes described above. The rate coefficient is characterized by a sharp negative T-dependence of the rate coefficient, owing to the reduced redissociation of the stabilized pre-reactive complexes at lower temperatures, and the increased contribution of product formation by tunneling at energies below the reactant energy. The exact temperature at which the sharp transition occurs is influenced by the uncertainties in the theoretical data; compared to the experimental data, the a priori predicted onset seems shifted by about -30 K.

5.3. Low pressure regime: k_LPL(T) and CH₂OH and CH₃O yields (T=20-400 K)

Fig. 3 also shows the temperature dependent rate coefficient in the low pressure regime, k_LPL(T). Here the product-forming reaction rate is determined solely by the complex capture rate coefficient (k_a), from which the fraction of redissociation to the free reactants is subtracted. The low-pressure rate coefficient is always lower than in the high-pressure regime; the underlying reason is that complexes with an energy content below the reactants can only undergo H-abstraction by tunneling, whereas complexes with an energy content equal to or above the reactants can always redissociate. Fig. 6 shows the energy-specific rate coefficients of the pre-reaction complex for redissociation and H-abstraction. Again, we can distinguish several distinct regimes.

Regime I: At high internal energies of the complex, E > E_TSb2, the redissociation rate coefficient becomes mostly energy-independent, nearing the limit of the vibrational frequency of the dissociation mode. The rates for H-abstraction increase steadily with higher energies, with k_b1(E) rising faster than k_b2(E) as the TS_b1 is lower in energy; tunneling is of less importance in this energy range.

Regime II: At somewhat lower internal energies, E_diss ≤ E ≤ E_TSb2, k_-a(E) drops sharply, as less excess energy is available compared to the dissociation limit; just below E_diss, redissociation becomes energetically impossible. k_b1(E) and k_b2(E) slow down as well, but due to tunneling they do not drop as sharply, increasing the effectiveness of product formation. CH₂OH + H₂O remains the dominant product, aided by its lower barrier height compared to TS_b2.

Regime III: Below the dissociation limit E_diss, where redissociation is impossible, the reaction proceeds by tunneling through the H-abstraction channels. In the low-pressure limit, however, energies below E_diss are not accessible due to the conservation of energy.

At minimal energies as relevant at the lowest temperature, i.e. just above the CH₃OH+OH reactants, redissociation is slower than H-abstraction (see Fig. 6), leading to an effective rate coefficient close to the capture rate coefficient; at 10 K, we estimate only 14% of redissociation contribution. As the energy population shifts to higher internal energies due to increasing temperatures, the rate coefficient through the loose redissociation TS (Fig. 5) increases faster than H-abstraction, leading to a decreasing yield of products. At even higher internal energies such as those populated at temperatures above 250 K, the difference between the rate coefficients for redissociation and product forming channels becomes smaller again, leading again to a higher probability of H-abstraction and hence a positive temperature dependence of the effective k(T). In the low-pressure regime, CH₂OH + H₂O is found to be the dominant product, with contributions of ~70% at 20 K, slowly rising to 80% at T ≥ 300 K (see Table S5). This contrasts to the high-pressure regime, as the tunneling contribution for the two H-abstraction pathways is more comparable at energies at or above the reactants, as opposed to deeper into the complex energy well. The lifetime of the complex is less than a microsecond (see Fig. 6) even at the lowest temperatures, decreasing to nanoseconds at room temperature and beyond.

5.4. Predicted Pressure Dependence of k(T)

The pressure-dependence of the rate coefficient is determined by collisional energy loss in the pre-reaction complex. All complexes have a nascent energy content sufficient for redissociation, but the reaction efficiency increases if the intermediates undergo collisional energy loss to energies below the redissociation threshold, where only H-abstraction can occur. Higher pressures thus lead to higher rate coefficients. The critical parameter to determine the pressure-dependence of this reaction is thus the lifetime of the complex at energies above the threshold; if this lifetime is shorter than the time needed for sufficient collisional energy loss, the reaction will be in the fall-off or low-pressure limit due to the contribution of redissociation. Fig. 6 compares the energy-specific reaction rates of the complex to the pseudo-first order collision frequency at two selected pressures and temperatures: 1 bar and 300 K and 1 mbar and 50 K; note that multiple collisions may be necessary to stabilize an energetically hot complex intermediate to below the dissociation limit.

At high energies, above 6 kcal mol^-1, redissociation is the fastest reaction, exceeding the collision rate even at 1 atm. At higher temperatures, the reaction can thus be in the fall-off or low-pressure regime even at atmospheric pressures. The impact on the overall rate coefficient is small: as indicated earlier, preventing tunneling through the H-abstraction transition states only affects the rate coefficient at room temperature by a factor of 2. The IUPAC¹⁰ recommendation of k(T) at atmospheric pressure is intermediate between our high- and low-pressure results. Indeed, in our predictions the nascent energy distribution at 300 K extends well into the energy regime where energy-specific redissociation exceeds the collision frequency at 1 atm, suggesting that the reaction might be in the fall-off regime. At low energies, however, the collision frequency at 1 atm is well above the rate of unimolecular reactions at energies near the dissociation limit, suggesting a high-pressure regime below 100 K. At 1 mbar, in contrast, the collision frequency is merely comparable in magnitude to the unimolecular rates for these energies, and in the experimental conditions used in this work, the reaction rate is then expected to be again in the fall-off to the low-pressure regime, depending on temperature. At the negligible pressures prevalent in the interstellar medium, the reaction rate will be strictly in the low-pressure regime. At intermediate temperatures and intermediate pressures, the rate coefficient will transition between the high- and low-pressure regimes. We did not attempt to calculate pressure-dependent rate coefficients explicitly, as these predictions would be critically dependent on the collision model and its energy transfer parameters; these cannot be determined a priori with sufficient accuracy and would require fine-tuning against experimental data. Likewise, an accurate prediction of the pre-reaction complex state density at energies near or above the dissociation limit beyond the RRHO approximation would be necessary. The modes for relative wagging and rotation of the CH₃OH and OH moieties in the complex are highly anharmonic; simple estimates using uncoupled Morse oscillators for the three lowest-wavenumber modes rather than harmonic oscillator already decreases the unimolecular reaction rate coefficients by a factor of 2 to 3, with even further reduction expected when mode coupling, internal rotation, and perhaps roaming would be taken into account. The ratio of unimolecular reaction against collisional energy transfer in the pressure-dependent model then also needs calibration against experiment, losing predictive power and reducing the Master Equation analyses to a statistical fit.

5.5. Fitting the predictions to the experimental data

Even though our predictions suggest pressure-dependences in the experimental data, it is instructive to explore the predictions when fitting critical parameters to the experimental data. Firstly, we shift the energy of the transition states for H-abstraction such that the high-pressure predictions k_HPL match the IUPAC¹⁰ recommendations for the total rate coefficient at k(300 K), 9×10^-13 cm³ molecule^-1 s^-1, and for the 0.15 fraction contribution of CH₃O + H₂O formation. This requires increasing the TS energy for CH₂OH+H₂O formation by +0.209 kcal mol^-1, and lowering the TS for CH₃O + H₂O formation by -0.453 kcal mol^-1. Note that these changes are approximate; we have not recalculated the tunneling corrections. A second alteration is scaling the capture rate coefficient near the free reactants energy to match the average of the experimental data near 20 K, ≈ 6.8×10^-11 cm³ molecule^-1 s^-1; specifically, the rate coefficient is increased by a fitted factor 1.66 in the lowest 0.23 kcal/mol range, where the largest impact is expected due to the deficiencies of the RRHO approximation for the transitional modes at very large reactant separations (see methodology section). This leaves the capture rate coefficient virtually unchanged at room temperature as there this lowest energy band has little contribution to the population. The resulting k(T) is shown in Fig. S5, as designed the curve now matches the experimental data even better. It is interesting that the high-pressure limit k(T < 100 K) now shows the experimentally observed, somewhat steeper negative T-dependence, and that the sharp transition in regime III coincides better with the experimental data. The change in the relative TS barrier heights also leads to an increase in the yield of CH₃O + H₂O in the LPL, now constituting 50 % of the product formation below 100 K (see Table S6).

The required changes to the PES are not outside the a priori expected reliability of the quantum chemical data. The required changes on the TSb₂ barrier are rather large for the high level of theory used, but this could also be partly due to our approximations regarding anharmonicity, internal rotation, multi-dimensional tunneling, due to the higher multi-reference character of its wavefunction,¹⁹ or because the target CH₃O yield at 300 K is rather uncertain: 0.15±0.10. The required change in the capture rate coefficient at the lowest energies is well within the uncertainty margin at excess energies below 0.25 kcal mol^-1, considering that the flatness of the PES at large reactant separations makes the calculations of the derivatives less accurate, and that the harmonic oscillator model is expected to yield too low a state density for the transitional modes. We thus found that the high-pressure limit can be fitted to the data across all temperatures without exceeding the expected uncertainties in the underlying theoretical model. At room temperature and above, we could likewise have chosen to fit the low-pressure predictions to the experimental data. Hence, we cannot state with full confidence that pressure-effects are at play, even though the a priori data suggests that pressure-effects should play a role in the experimental conditions. At low temperatures, ≤200 K, our low-pressure predictions are qualitatively different from the experimental observations, which strongly suggest that for those conditions, the experimental pressures are not low enough to reach the low-pressure regime.

5.6. Comparison with previous experimental and theoretical kinetic data

Figure 7 shows our experimental and theoretical k(T) together with those previously reported in the literature.

Since the pressure-dependence of k(T) is only experimentally affordable in a limited range and given the small difference between the high- and low-pressure regimes at room temperature, a rather large pressure range may be needed to unequivocally reach either limit. A direct comparison between the theoretical predictions and the experiments might thus be biased by pressure effects. For instance, at room temperature and beyond, the experimental data at atmospheric conditions is bracketed by our high- and low-pressure predictions, with the a priori predicted k_HPL(300 K) about a factor 1.3 above the IUPAC¹⁰ recommendations, and predicted k_LPL(300 K) a factor of 1.7 below. Earlier work by Gao et al.¹⁹ found a high-pressure rate coefficient that matches the experimental data better. While the quantum chemical data in our study is of higher quality than used by Gao et al.,¹⁹ their theoretical kinetic model is more rigorous, incorporating anharmonicities, internal rotors, and multi-dimensional tunneling. Thus, while the two PESs are directly comparable, this may result in different rate coefficient predictions by a small factor, as found here. The high-pressure H-abstraction rate coefficient from the pre-reactive complex predicted by Gao et al.¹⁹ at 300 K, k(300 K)=3×10⁸ s^-1, is comparable to ours, k(300 K)=1.9×10⁸ s^-1, and while these authors do not provide energy-specific rate coefficients, it seems likely that their data would likewise lead to a fall-off regime for the higher-energy nascent population found at these temperatures and beyond. The Master Equation analysis by Shannon et al.¹⁴ incorporates collisional energy loss and predicts values between our HPL and LPL limit, and closer to the LPL limit consistent with their observation that collisional energy transfer has only a small influence in their study.

At low temperatures, our high-pressure predictions are a factor of 2.2 below the highest measured rate coefficients. As already discussed higher, our methodology is expected to underestimate the capturing rate coefficient by a small factor due to inadequacies of describing the entropy of the approaching reactants at large separations. Still, our a priori prediction finds a slightly negative T-dependence below 100 K, qualitatively and semi-quantitatively in agreement with the experiments. As shown above, a small adjustment of the large-distance entropy results in a higher rate coefficient and a somewhat steeper negative T-dependence; note that the energy-specific rate coefficients suggest that part of the observable negative T-dependence could also be due to fall-off effects, with measurements at lower temperatures being closer to the high-pressure regime due to less redissociation contribution.

The prediction of the low-pressure regime appears to be highly dependent on the theoretical methodology used, with large differences across the literature data and our work both in the temperature-dependence of k(T), as in the apparent limiting value at 0 K. Our kinetic model of the capture reaction incorporates both the attractive energy potential between the reactants, as well as the entropic change along the reaction coordinate; this results in the well-known negative T-dependence for barrierless reactions. Gao et al.¹⁹ used a hard-sphere collision model, omitting the entropic factor; their value is thus an upper bound only, unlikely to be valid except near 0 K. Most of the difference between our predictions is then due to our more rigorous capture model, where a lower capture rate coefficient implies a lower redissociation rate based on micro-reversibility arguments, and hence a higher low-pressure rate coefficient due to a higher contribution of H-abstraction.

Our LPL results can be compared as well to those recently presented by Roncero et al.²¹ who used the QCT method which, by essence, excludes collisions with a third body. The results of the QCT are plotted in Fig. 7. As it can be seen, the reaction rate coefficients calculated by Roncero et al.²¹ between 10 K and 400 K are significantly higher than the LPL model from Gao et al.¹⁹ (a factor of 5-10 larger) and either higher than the present study (T>80 K) or lower (T<80 K) with a crossing point at about 80 K. They remain much lower than the experimental data especially below 160 K. Furthermore, the computed k(T) by Roncero et al.²¹ is almost temperature independent, which disagrees with the other theoretical LPL predictions. Roncero et al.²¹ remark that, in their work, the pre-reactive complex lifetime is probably underestimated because quantum effects such as tunneling and zero point energy have not been taken into account in the simulations. Furthermore, the potential energy surface used by Roncero et al.²¹ deviates most from the author studies (see Table S7).

The theoretical calculations all indicate that CH₂OH + H₂O is the dominant product in the HPL at room temperature, but that CH₃O + H₂O becomes the dominant channel as the temperature lowers, and that tunneling is the driving factor both for this product yield increase, as for the increase in the total rate coefficient. The results are thus qualitatively consistent with the observation of CH₃O by Shannon et al.¹⁴ at their lowest temperatures, even if the predicted yields vary somewhat on the methodology used. In the LPL, CH₂OH is predicted to be the dominant product across all temperatures.

6. Astrophysical implication

Chemical reactions in interstellar clouds, particularly dense molecular clouds, are responsible for the formation of a majority of important astronomical molecules including complex organic molecules (COMs). These reactions can be divided into two groups, gas phase and grain surface processes. A number of COMs, for example, glycolaldehyde, formamide, formaldehyde, amino acetonitrile, methanol, acetic acid, and methylamine, have been detected in the gas phase of cold interstellar clouds.^54–66 Surface chemistry fails to explain their abundances.

Chemical kinetics experiments have demonstrated that many radical–neutral reactions are very rapid at low temperatures in the gas phase and, thus, play an important role in the interstellar chemistry.^12,23,32,67 The CH₃OH + OH reaction may play a crucial role in the formation of other species in the ISM^1,3,4 including COMs such as methyl formate and dimethyl ether.¹ The mentioned reaction has been included in models with estimated rate coefficients close to our measurements, but typically with only CH₃O + H₂O as products, following the detection of CH₃O by Shannon et al.¹⁴ However, according to our new data, CH₂OH remains a significant daughter species at the lowest temperatures, contrary to the previous conclusions. A full review of the chemistry of the product radicals is beyond the scope of the current work, and the impact of our findings can only be quantified by incorporation of these results into a suitable chemical model and compare the results against earlier models in a set of relevant scenarios. Still, we shortly examine the main implications of our findings.

CH₃O radicals have been recently detected in cold dark clouds,⁶⁸ while, to our knowledge, CH₂OH has not been observed in the ISM. As CH₂OH is the most stable of the product isomers, it will not isomerize to CH₃O by either tunneling or H-atom exchange, due to the reaction endothermicity of ~10 kcal mol^-1.⁶⁹ Unimolecular decomposition to CH₂O + H is highly endothermic and very slow.⁷⁰ Regeneration of methanol by reaction with H-atoms is ineffective in the gas phase due to the need for stabilization of the hot adduct. More likely, reactions in the gas phase are H-abstraction reactions from H₂ or other organic species or by reactions on the surface of dust grains [see e.g. Álvarez-Barcia et al.⁷¹ and references therein], forming CH₂O.

On the other hand, reactions of CH₂OH with other organic radicals can lead to the formation of COMs such as ethylene glycol (HOCH₂CH₂OH), glycolaldehyde (HCOCH₂OH) or other hydroxy-substituted organics. The main consequence of the predicted formation of CH₂OH instead of exclusively CH₃O in the title reaction is, thus, a shift towards hydroxylated organics rather than carbonyl- or alkoxy-bearing compounds in the ISM. Such hydroxylated compounds are more amenable to H-bonding, which could lead to longer-lived complexes with other organic molecules, ions, or oxygenated radicals. This, in turn, can enhance the overall organics reactivity through H-bond assisted chemistry (as exemplified in this work for CH₃OH + OH), or by the ability for dissociative cooling in hot reaction products by breaking of the complex.

Results of the present study allowed us to evaluate, complete, and reveal the dependence of the rate coefficient for the CH₃OH + OH reaction in the temperature range 177.5 – 11.7 K corresponding to the temperatures in interstellar clouds from diffuse through translucent to dense. Higher temperature values are also reliable for outer parts of circumstellar shells and disks. The capture limit reached at temperatures below 22 K allows one to apply our results to the coldest objects in the universe, such as the Boomerang Nebula.

7. Conclusions

In this work, the temperature dependence of the rate coefficients of the gas-phase OH+CH₃OH reaction has been investigated from 11.7 K to 177.5 K using the CRESU technique. The wide temperature range investigated allows one to have a complete picture of the kinetic behavior of this chemical system. It has been confirmed that the temperature dependence of k(T) below 120 K is less pronounced than between 200 K and 120 K. The experimental and theoretical results converge toward a mechanistic understanding in which the reaction evolves from a fall-off regime between ~160 and ~120 K, (demonstrated by the pressure dependence observed experimentally and theoretically) to a high pressure regime below 120 K where no experimental pressure dependence was seen within the experimental uncertainties and where the theoretical HPL calculation matches the measurements satisfactorily. At the lowest temperatures, the theoretical results indicate that k_HPL and k_LPL both converge to a capture limit showing that the reaction becomes practically pressure independent at around 10 K. The pressure dependence of the title reaction is dramatically controlled by the lifetime of the pre-reactive complex at energies above the energy of the reactants threshold, but the predicted lifetime, and hence the P-dependence, is strongly dependent on the methodology. The predicted HPL rate coefficients at the lowest temperatures (T<40 K) carry a larger uncertainty although they remain within a factor of about 1.6 of the experimental data at 20 K, and can be easily reconciled with the experimental data by minor adjustments of the entropy factor at large reactant separations.

Branching ratios leading to the two exit channels CH₂OH + H₂O and CH₃O + H₂O have been determined theoretically as a function of temperature, indicating that CH₂OH remains significant at the lowest temperatures in the LPL, contrary to the preceding conclusions found in the literature. At 80 K, our HPL calculations predict that the CH₃O radical is largely the main product formed in qualitative agreement with the CH₃O experimental detection by Shannon et al.¹⁴ Below 40 K, the value of the branching ratio is very uncertain as it is highly depending on the methodology used, and no recommendation is made. In the LPL regime reigning in the interstellar medium, the branching ratio for the production of CH₂OH has been found to be about 70% at 20 K (probably extendable to lower temperatures) using the a priori methodology. However, adjusting the TSs barrier heights, in order to fit the HPL predictions to the recommended rate coefficient at 300 K and the CH₂OH branching ratio, and scaling the low-energy capture rate coefficient in order to better match the experimental results at 20 K, leads to a branching ratio reduced to 50% at 20 K for the CH₂OH product, indicating that the yield prediction still carries a factor 2 uncertainty due to our treatment of the features of the potential energy surface, and the impact of pressure. From an astrophysical point of view, the present experimental results confirm the rate coefficient inferred at 10 K from extrapolation in the work by Antiñolo et al.¹². The theoretical LPL calculations indicate, however, that the channel leading to CH₃O radical is unlikely to be 100% at 10 K as believed until now and may be reduced by a factor of 2 to 3.

Although the present work brings a significant amount of important information to enlighten the mechanisms driving the reaction of OH with methanol, there is still place for complementary investigations. From a theoretical point of view, taking into account anharmonicities, improving the description of transitional modes, considering more elaborate tunneling corrections, and accounting for pressure effects could reduce the uncertainty of the predictions. From an experimental point of view, it becomes more and more important to be able to detect the products and quantify the branching ratios as a function of temperature and more specifically at temperatures as close as possible to 10 K. Laser induced fluorescence techniques are usually not appropriate for this kind of investigation because they do not deliver an absolute value of the product density and not all products present a LIF spectrum. Although the methoxy radical presents a LIF spectrum, its LIF detection at the lowest temperatures would only confirm that the channel leading to CH₃O + H₂O is open. A combination of the chirped pulsed microwave spectroscopy and CRESU techniques developed in A. Suits' group is a promising method that should be able to detect and quantify a large number of polar molecules by microwave absorption.⁷² A new apparatus, coupling this technique to a CRESU reactor, is presently in construction in the Rennes group in France. Mass spectrometry techniques are also of great interest provided that a tunable frequency source is used in order to photoionize the products without fragmenting them. In the Rennes group, a dedicated CRESU chamber has been built and has been implemented at the Soleil Synchrotron in order to accomplish this challenging task (S.D. Le Picard et al. in preparation).

Supplementary Material

The Supplementary Information contains the following information: detailed experimental methodology, experimental conditions employed in the kinetic study, operational conditions of the Laval nozzles, and supporting figures including LIF spectrum of OH radicals at 11.7 K, spatial profiles of the jet temperature and optical measurement of methanol. Tables with computed rate coefficients and product yields for the reaction steps in the CH₃OH + OH mechanism, IRC energy profiles and raw quantum chemical information are also included in the Supplementary Information.