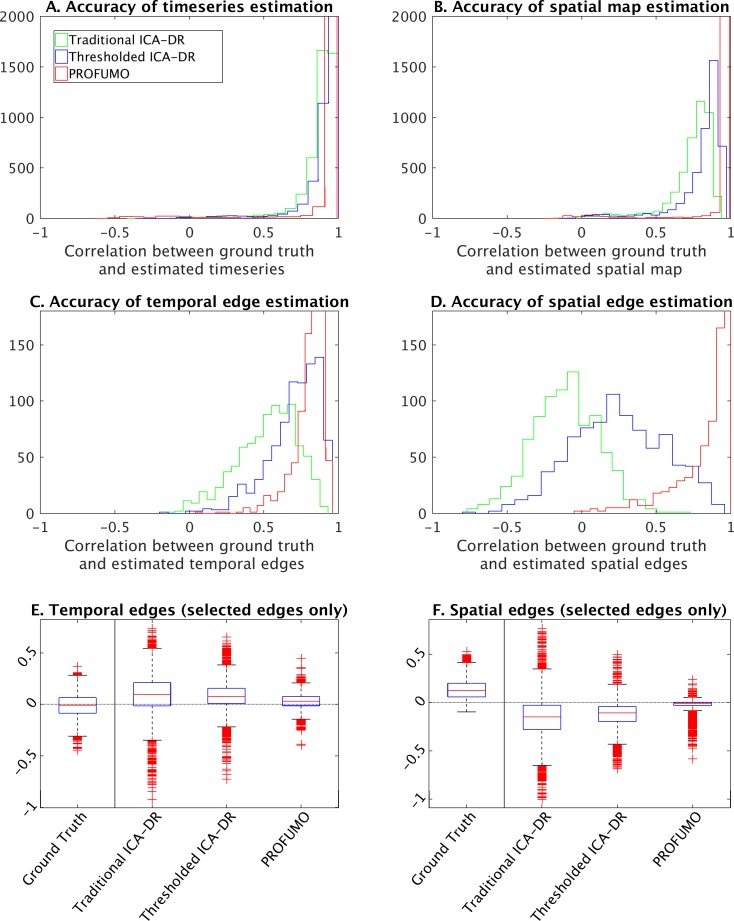
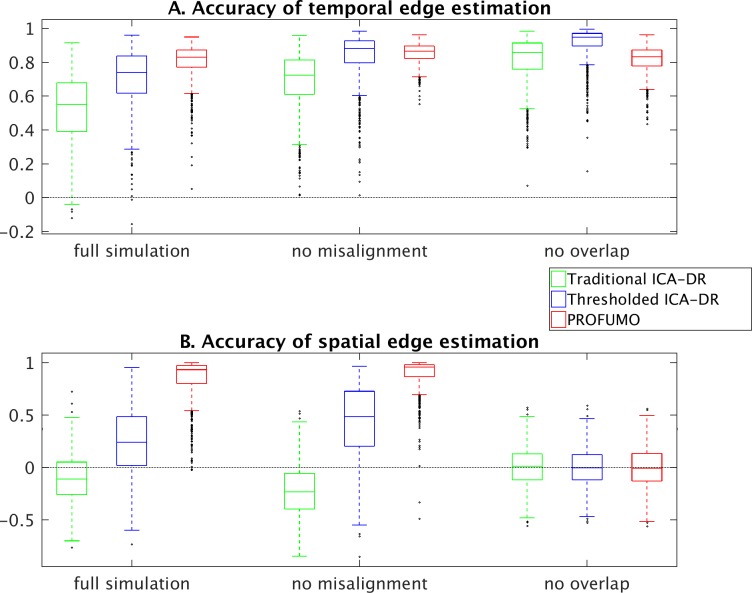
Figure 7. Simulation results to compare traditional ICA-DR, thresholded ICA-DR, and PROFUMO performance.

(A) Correlations between ground truth and estimated subject timeseries is high across all three methods. (B) Correlations between ground truth and estimated subject spatial maps is highest in PROFUMO results (red), and improved in thresholded ICA-DR results (blue) compared to traditional ICA-DR results (green). Similar results are found for cross-subject correlations of temporal network matrix edges (C), and for cross-subject correlations of spatial overlap matrix edges (D). Results in A-D are shown for all maps that achieved a minimum group-average spatial correlation between ground truth and estimated maps of r = 0.5 across the three methods. Figures E and F show results for a subset of edges with significantly positive spatial correlation. Here, the first ‘ground truth’ column shows the distribution of ground truth edge strengths, whereas columns 2–4 show the difference between estimated and ground truth edge strengths (i.e., results in columns 2–4 that are closest to zero are best).

Figure 7—figure supplement 1. Comparison across different simulations for the accuracy of temporal edge estimation (A), and for the accuracy of spatial edge estimation (B).

The ‘full simulation’ included both spatial overlap and spatial misalignment (this matches the results in Figure 6). The ‘no misalignment’ simulation was run with identical parameters, except that there was no misalignment between subjects. The ‘no overlap’ simulation was again run with identical parameters, except that spatial maps were forced to be uncorrelated at the level of individual subjects by running spatial ICA at this stage in the simulation prior to generating the data. Results show similar biases in spatial and temporal edge estimates from standard dual regression in the full and no misalignment simulations, indicating that this effect is observed irrespective of spatial misalignment. The no overlap simulation also shows improvement of thresholded dual regression over standard dual regression, likely as a result of the effective reduction of noise that is achieved when thresholding the maps. Note that there are no meaningful spatial edges in the ‘no overlap’ simulation, so it is expected that none of the methods estimate this.