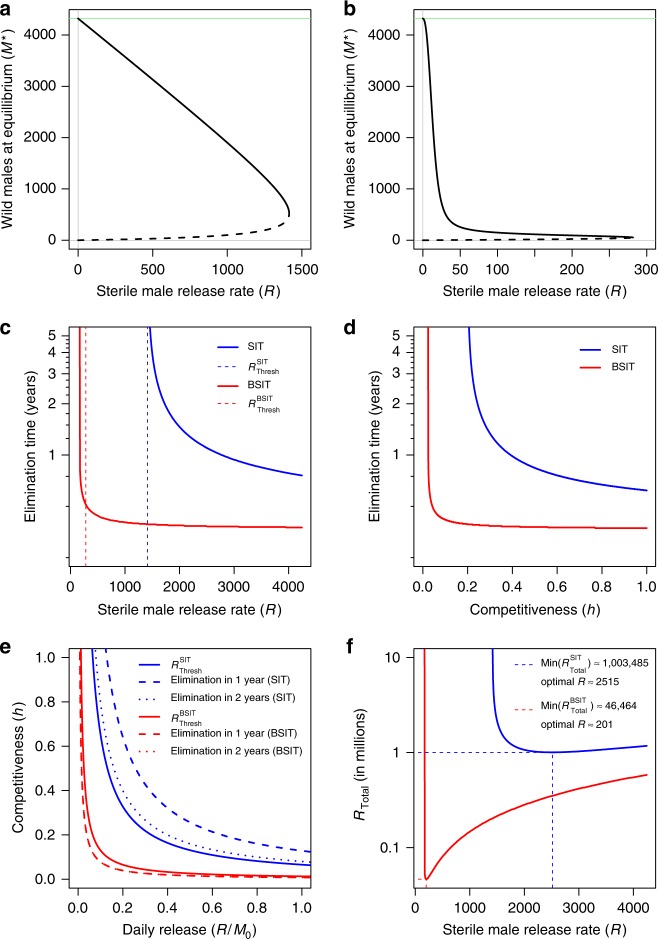
Fig. 1.

Equilibria, thresholds and optima of the BSIT model. Density of males at stable (solid lines) and unstable (dashed lines) equilibria given release rate (R) under SIT (a) and BSIT (b). A bifurcation, where stable and unstable equilibria converge, provides an elimination threshold for SIT $\left(R_{\mathrm{Thresh}}^{\mathrm{SIT}}=1414.7\right)$. Pyriproxifen reduces the threshold $\left(R_{\mathrm{Thresh}}^{\mathrm{BSIT}}=281.6\right)$ and the distance between stable and unstable equilibria (b). With SIT, elimination time grows asymptotically at $R_{\mathrm{Thresh}}^{\mathrm{SIT}}$ (blue dashed), whereas boosting can shift this asymptote below $R_{\mathrm{Thresh}}^{\mathrm{BSIT}}$ (red dashed) (c). With R fixed (R = 1414), elimination time responds asymptotically to competitiveness (d), and boosting shifts the threshold (h_Thresh) towards zero. Thresholds for the eventual elimination of any initial population (solid), and for eliminating from carrying capacity in one (dashed) or two (dotted) years respond non-linearly to release rate (R) and competitiveness (h) (e). Two years (dotted) and 1 year (dashed) elimination thresholds for BSIT (red) are indistinguishable. The total release required for elimination (R_Total) is minimised at $1.8\times R_{\mathrm{Thresh}}^{\mathrm{SIT}}$ and $0.7\times R_{\mathrm{Thresh}}^{\mathrm{BSIT}}$ for SIT and BSIT, respectively (f, dashed lines). All simulations were initialised at carrying capacity, with M₀ the initial density of males