Figure 4.

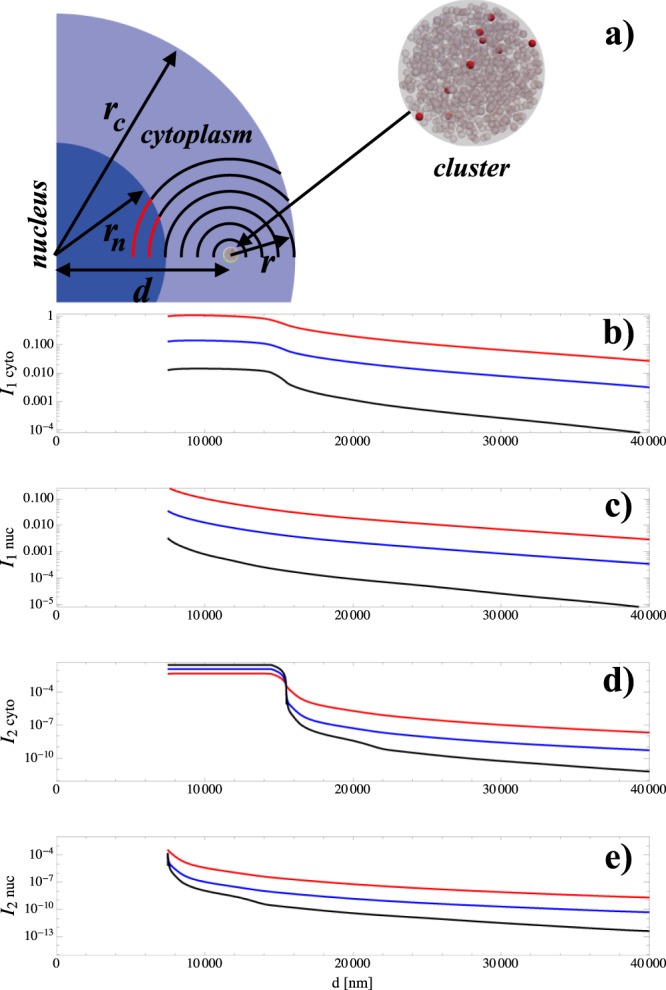
Calculation of the integrals I₁ and I₂ for a model spherical cell. (a) Illustration of the geometry under consideration with a 7 μm nuclear radius (r_n) and a 15 μm cell radius (r_c). A single cluster is ‘injected’ into the cell at a distance d from the centre of the cell. For a given distance r from the cluster, there is an arc of a circle which lies inside the nucleus (shown in red) and another insider the cytoplasm (shown in black). The solid angle created by rotating each of these arcs about the x-axis gives Ω(r) for the nucleus and cytoplasm respectively. Clearly Ω(r) is a function of d but is independent of the entities loading the cluster. More details of the functional form of Ω(r) are given in Supplementary Information. (b–e) show values of the integrals for both choices of critical volume, for clusters comprised of each of the nanoagents. All of these values have been normalised to the value of I₁ when the cluster formed of 25 nm nanoparticles is just at the edge of the nucleus when the whole cell excluding the cluster is the critical volume, i.e. everything is normalised with respect to the 25 nm nanoparticles’ cluster.