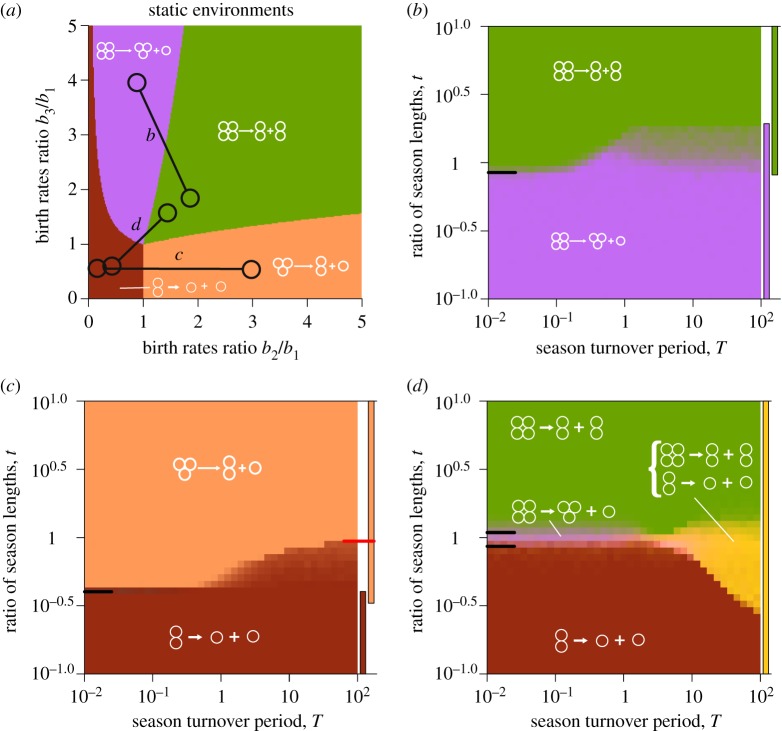
Figure 3.

Evolutionary optimality of life cycles in extreme regimes can be described by analytical approximations. (a) The dynamic environment used in panels (b–d) are represented by connected circles. (b) The optimality map featuring only pure life cycles. When season 1 is much longer than season 2, t ≫ 1, regardless of the overall seasons turnover length, the optimal life cycle is always the pure life cycle 2 + 2. For the opposite case, t ≪ 1, 3 + 1 is always optimal. For short seasons, T ≪ 1, the border between two life cycles is located at the position predicted by the short seasons approximation (black tick line on the left side of the map). For long seasons T ≫ 1, for this dynamic environment, the transition between two life cycles is performed through the bi-stability between pure life cycles, as suggested by long seasons approximation (see main text). Coloured bars on the right side of the map show the areas of stability of pure life cycles according to the long seasons approximation. (c) The optimality map featuring a mixed life cycle at the long seasons regime. For t > 0.287, pure life cycle 1 + 1 is not evolutionarily optimal, yet the mixed life cycle featuring pattern 1 + 1 persists up to t = 0.485, where it disappears in a saddle-node bifurcation indicated by a red mark (see main text). (d) The pure life cycles 1 + 1 and 2 + 2 can be executed within the same mixed life cycle at different seasons (see main text), and such a combination (yellow) might be evolutionarily optimal in the long seasons regime. Exact parameters used in calculations and simulations are presented in electronic supplementary material, appendix L. (Online version in colour.)