The N-flagella problem: elastohydrodynamic motility transition of multi-flagellated bacteria

Abstract

Peritrichous bacteria such as Escherichia coli swim in viscous fluids by forming a helical bundle of flagellar filaments. The filaments are spatially distributed around the cell body to which they are connected via a flexible hook. To understand how the swimming direction of the cell is determined, we theoretically investigate the elastohydrodynamic motility problem of a multi-flagellated bacterium. Specifically, we consider a spherical cell body with a number N of flagella which are initially symmetrically arranged in a plane in order to provide an equilibrium state. We solve the linear stability problem analytically and find that at most six modes can be unstable and that these correspond to the degrees of freedom for the rigid-body motion of the cell body. Although there exists a rotation-dominated mode that generates negligible locomotion, we show that for the typical morphological parameters of bacteria the most unstable mode results in linear swimming in one direction accompanied by rotation around the same axis, as observed experimentally.

1. Introduction

Bacteria, which constitute the largest domain of prokaryotic microorganisms, have survived for billions of years due to their sophisticated structures [1–3]. Many bacteria are motile and various forms of bacterial motility have been discovered, including gliding, twitching and swarming [4–7]. Above all, the most common form is swimming and both its hydrodynamics basis and the chemotactic behaviour of cells have been investigated for many decades [8–12].

Bacterial swimming is achieved using propulsion from helical appendages, called flagellar filaments, attached to the cell body (typical diameter ≈1–2 mm). A flagellar filament is a slender polymer, made of a single protein called flagellin, which takes the form of a rigid helix (typical length ≈10 mm and diameter ≈40 nm), driven in rotation by a bacterial rotary motor located at the base end of the filament. The numbers and positions of the flagellar filaments can vary greatly from cell to cell, but so-called peritrichous bacteria possess multiple flagella effectively randomly distributed on the cell surface. This group of bacteria includes well-studied organisms such as Bacillus subtilis, Salmonella enterica and the most popular model bacterium, Escherchia coli [9,10,13].

The behaviour of a rotary motor is regulated by inter-cellular signalling proteins. When a peritrichous bacterium is swimming (so-called ‘run’), the distributed flagellar filaments rotate in the same direction and gather together in a helical bundle, generating essentially linear propulsion. When at least one of the rotary motors counter-rotates, the bundle of flagellar filaments comes apart and the cell changes its orientation [14] (‘tumble’). The resulting well-studied run-and-tumble mechanism allows peritrichous bacteria to explore chemically their environment.

Owing to the small size of bacterial cells, the typical Reynolds number around a swimming bacterium is Re ≈ 10⁻⁴ and, as a result, the fluid flow obeys the incompressible Stokes equations, which are time-reversible. The ability of bacteria to reorient requires them to break the time-reversibility constraint (i.e. the scallop theorem [11]), which is enabled by a short flexible hook (≈60 nm in length) that connects the rotary motor to the semi-rigid flagellar filament. The motor/hook/filament complex is known as a flagellum. The flexibility of the hook allows it to behave as a universal joint [15] and is essential for flagellar bundle [16]. During the swimming motion, the flexible hook can buckle, providing a rich spectrum of swimming behaviours [17–21].

These mechanical structures together with the randomly distributed rotary motors of a peritrichous bacterium raise a fundamental question: In which direction does the cell move for a given motor configuration? The dynamics of a cell resulting from the rotating propulsion of multiple rotating objects (the flagellar filaments) could be referred to as N-flagella problem in reference to the classical N-vortex problem on the dynamics of point vortices [22]. The flagellar morphologies, including pitch size and the radius of the helical filament, fall onto one of a small number of polymorphic shapes, which have been characterized experimentally [23] while the flagellar length can vary greatly within species and cell populations. Despite these variations, a coherent flagellar bundle is expected to be maintained generically by long-range hydrodynamic interactions [24,25].

Recently, Riley et al. [26] demonstrated theoretically that the swimming of peritrichous bacteria is enabled by an elastohydrodynamic instability. Modelling a bacterium as propelled by multiple rigid helical filaments spatially distributed around the cell body and connected to it by linear torque springs, they showed that the coupling between the flagellar propulsive force pushing the cell body and the hydrodynamic forces resulting from the swimming motion could result in an elastohydrodynamic instability of the hook and lead to bacterial swimming towards a preferred direction. This motility transition, demonstrated numerically, was also explained by a theoretical model of a bacterium propelled by two rod-like flagella connected to the spherical cell body from opposite sides [26]. The critical value predicted by the linear stability analysis was in good agreement with the full computational simulations, suggesting that the swimming direction of peritrichous bacteria might be set by the stability of an equilibrium distribution of flagellar filaments.

The aim of the current paper is to formalize this physical result mathematically and to derive rigorously the elastohydrodynamic motility transition theory for a cell with an arbitrary number of flagella of arbitrary shape using linear stability analysis. In the theoretical model of [26], the rod-like flagella only generate forces, which the issue of torque generation was not considered. Since flagellar propulsion is generated by the rotation of helical filaments, a generation of torque is inevitable and we include it in this paper. The number of flagella is set to any integer N greater than 1 and we will consider equilibria and stability for the spatial distribution of the flagella.

The paper is organized as follows. Section 2 is devoted to the theoretical formulation of the problem. In §2a, we formulate the bacterial motility problem for a cell with N flagella, considering both force and torque balance for the cell and each flagellum. In §2b, we proceed to simplify the problem by focusing on the case of identical flagellar filaments generating axisymmetric propulsion. The latter property holds for a helical filament assuming that the time scale of the bending and rotation of the flagella are well separated, which is verified in practice. The typical flagellar rotation frequencies are ≈100 Hz and sufficiently faster than the typical frequency of cell rotation, ≈10 Hz, that we may approximate the flagellar propulsion by its time-average. We then consider the case where the N flagella are symmetrically distributed in a plane around the cell body and we focus on its linear stability from the equilibrium configuration, which is presented in §2c. The following sections are devoted to discussions of the results of the linear stability analysis. We first neglect small chirality effects in order to simplify the system, and in §3 we start our analysis with the case of N = 2 flagella, which is found to be different from the general case with N > 2 due to the symmetry of the flagellar distribution. The general case is then discussed in §4, where we start with the examples of N = 3 and N = 4 before deriving rigorously the general stability results. Finally, we reincorporate the effects of chirality in §5 where solve the full problem.

2. Mathematical model of peritrichous bacterium

(a). Equations of motion

In this first section, we describe the force and torque balance equations, together with the torque balance of each elastic spring and hydrodynamic drag on each flagellar filament, in order to formulate a linear problem of 2N + 6 dimensions for bacterial motility propelled by rotating flagella.

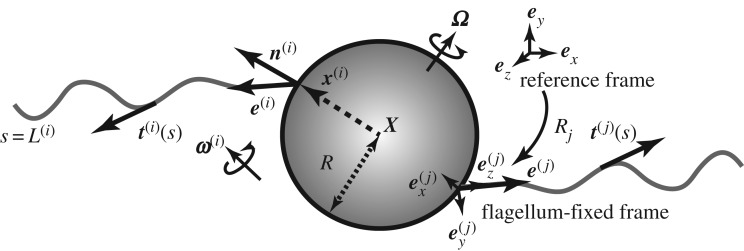
We consider a swimming bacterium located in a Newtonian fluid of constant dynamic viscosity μ. The cell body is assumed to be a sphere of radius R. We denote the centre of the sphere by X and its orientation by a unit vector e. The bacterium is assumed to possess N rigid flagellar filaments connected to the cell body at their base. The direction for the axis of each filament is measured by the unit vectors e⁽ⁱ⁾ for ith flagellum (i = 1, 2, …, N), as schematically illustrated in figure 1. We label each flagellar filament using the arc length, s∈[0, L⁽ⁱ⁾], measured from the flagellum–cell body connection (i.e. the location of the motor), where L⁽ⁱ⁾ is the length of the ith flagellum, whose shape is determined by its tangent vector t⁽ⁱ⁾(s).

Figure 1.

Schematic of the model multi-flagellated bacterium considered in this paper (see text for details).

(i). Force balance for a whole cell

We first consider the force balance equations for the entire cell, which, in the absence of inertia, state that the sum of the hydrodynamic forces on the cell body and all flagella must add up to zero.

Let U and Ω be the linear and angular velocities of the cell, respectively. Neglecting hydrodynamic interactions between the cell body and the flagellar filaments, the hydrodynamic drag on the cell body, F_body, is simply given from the Stokes Law, by F_body = C_DU, where C_D = − 6πμR and hereafter we non-dimensionalize the length scale using R = 1.

The hydrodynamic force on the ith flagellum, F⁽ⁱ⁾, is obtained from the resistive-force theory of slender filaments, which predicts that the hydrodynamic force on a small segment of the flagellum, dF, is linearly related to its local velocity relative to the background fluid, u⁽ⁱ⁾, as

$$\mathrm{d}{\mathit{F}}^{(i)}(s)=[C_t{\mathit{t}}^{(i)}{\mathit{t}}^{(i)}+C_n(\mathbf{1}-{\mathit{t}}^{(i)}{\mathit{t}}^{(i)})]\cdot {\mathit{u}}^{(i)}(s)\hspace{0.17em}\mathrm{d}s,$$ 2.1

where C_t and C_n are the negative drag coefficient constants whose values depend on the flagellar slenderness parameter [27,28]. Here, the local velocity u⁽ⁱ⁾ is the sum of the velocities of the cell body and the flagella. Introducing the angular velocity of each flagellum as ω⁽ⁱ⁾ (figure 1), we have

$${\mathit{u}}^{(i)}=\mathit{U}+\mathit{\Omega }\times ({\mathit{x}}^{(i)}+{\mathit{\xi }}^{(i)})+{\mathit{\omega }}^{(i)}\times {\mathit{\xi }}^{(i)},$$ 2.2

where

$${\mathit{\xi }}^{(i)}(s)={\int }_0^s{\mathit{t}}^{(i)}(s^{\prime })\hspace{0.17em}\mathrm{d}{s}^{\prime }$$ 2.3

is the position along the flagellar segment at arc length s. From (2.2), integrating over the entire flagellar filament leads to the hydrodynamic force on the ith flagellum, with denoting the drag coefficient tensor in (2.1) by C_i, given by

$${\mathit{F}}^{(i)}=[{\int }_0^{L^{(i)}}{\mathsf{C}}_i\hspace{0.17em}\mathrm{d}s]\cdot \mathit{U}+[{\int }_0^{L^{(i)}}{\mathsf{C}}_i\cdot {\mathsf{A}}_i\hspace{0.17em}\mathrm{d}s]\cdot \mathit{\Omega }+[{\int }_0^{L^{(i)}}{\mathsf{C}}_i\cdot {\tilde{\mathsf{A}}}_i\hspace{0.17em}\mathrm{d}s]\cdot {\mathit{\omega }}^{(i)}.$$ 2.4

Here, we have introduced skew-symmetric matrices A_i and ${\tilde{\mathsf{A}}}_i$ whose components are given, respectively, by

$${\left[{\mathsf{A}}_i\right]}_{pq}={\epsilon }_{pqr}(x_r^{(i)}+{\xi }_r^{(i)})\mathrm{and}{\left[{\tilde{\mathsf{A}}}_i\right]}_{pq}={\epsilon }_{pqr}{\xi }_r^{(i)},$$ 2.5

where ε_pqr is the Levi–Civita symbol and the Einstein summation convention is used over the repeated indices (p, q, r = 1, 2, 3). The final force balance equations obtained by summing up the forces as

$${\mathit{F}}_{\mathrm{body}}+\sum _{i=1}^N{\mathit{F}}^{(i)}=\mathbf{0}.$$ 2.6

(ii). Torque balance for a whole cell

Similar to the above arguments, we now derive the expressions for the torque balance for an entire cell at the centre of the cell body. We again neglect hydrodynamic interactions between the cell and flagella and model hydrodynamic drag on each flagellar filament at the level of resistive force theory (RFT).

The torque acting on the spherical cell body is given by M_body = C_RΩ, where the resistance coefficient is C_R = − 8πμR³. The hydrodynamic torque on a segment of a flagellum is given by dM⁽ⁱ⁾ = (x⁽ⁱ⁾ + ξ⁽ⁱ⁾) × dF⁽ⁱ⁾, which yields the total torque expression after an integration over the flagellum as

$${\mathit{M}}^{(i)}=[{\int }_0^{L^{(i)}}{\mathsf{A}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\hspace{0.17em}\mathrm{d}s]\cdot \mathit{U}+[{\int }_0^{L^{(i)}}{\mathsf{A}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\mathsf{A}}_i\hspace{0.17em}\mathrm{d}s]\cdot \mathit{\Omega }+[{\int }_0^{L^{(i)}}{\mathsf{A}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\tilde{\mathsf{A}}}_i\hspace{0.17em}\mathrm{d}s]\cdot {\mathit{\omega }}^{(i)},$$ 2.7

where the superscript, T, indicates the transpose of a matrix. Note that in order to obtain that expression, we neglected the torque arising from local rotation of the flagellar filaments around their centreline, which is typically orders of magnitude smaller than (2.7) in the experimental limit where the radius of the helical centreline is much larger than the thickness of the filament.

The overall torque balance equation for the whole cell is then written as

$${\mathit{M}}_{\mathrm{body}}+\sum _{i=1}^N{\mathit{M}}^{(i)}=\mathbf{0}.$$ 2.8

(iii). Torque balance for each flagellum

We proceed to consider the torque balance relation for each flagellum, which experiences both hydrodynamic torque and an elastic spring restoring torque at the flagellum–cell body junction [26,29]. The hydrodynamic torque follows from the discussion above and we now consider the torque balance at the flagellum–cell body junction point. The torque acting on a segment of a flagellum is then given by $\mathrm{d}\tilde{\mathit{M}}={\mathit{\xi }}^{(i)}\times \mathrm{d}{\mathit{F}}^{(i)}$ and integrating over the flagellum yields the hydrodynamic torque

$${\tilde{\mathit{M}}}^{(i)}=[{\int }_0^{L^{(i)}}{\tilde{\mathsf{A}}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\hspace{0.17em}\mathrm{d}s]\cdot \mathit{U}+[{\int }_0^{L^{(i)}}{\tilde{\mathsf{A}}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\mathsf{A}}_i\hspace{0.17em}\mathrm{d}s]\cdot \mathit{\Omega }+[{\int }_0^{L^{(i)}}{\tilde{\mathsf{A}}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\tilde{\mathsf{A}}}_i\hspace{0.17em}\mathrm{d}s]\cdot {\mathit{\omega }}^{(i)}.$$ 2.9

As a model for the elastic hook, a linear spring torque is assumed to be present at the junction point. Let κ⁽ⁱ⁾ > 0 be the spring constant and let the relative angle difference from the initial orientation be denoted by θ⁽ⁱ⁾. The elastic torque on each flagellum can be then written as

$${\mathit{M}}_{\mathrm{elast}}^{(i)}=-{\kappa }^{(i)}{\theta }^{(i)}{\mathit{e}}_{\perp }^{(i)},$$ 2.10

where e⁽ⁱ⁾_⊥ is the unit vector perpendicular both to the initial and current flagellar orientation vectors. In the later part of this manuscript, we will assume that the flagellar orientations initially coincide with the outward normal n⁽ⁱ⁾ (figure 1), but the formulation here does not necessarily assume this initial condition.

Hereafter, we assume that each flagellum is rotated at a fixed rate and thus the torque balance equation for each flagellum is obtained as the instantaneous balance

$${\mathsf{P}}_i\cdot {\tilde{\mathit{M}}}^{(i)}+{\mathit{M}}_{\mathrm{elast}}^{(i)}=\mathbf{0},$$ 2.11

where we note that only the torque balance perpendicular to the vector e⁽ⁱ⁾ is considered, where P_i = (1 − e⁽ⁱ⁾e⁽ⁱ⁾) is the projection onto the plane perpendicular to e⁽ⁱ⁾.

Note that if, alternatively, one was to model swimming as induced by motors rotating at fixed torque [20,24], we would need an additional term in the torque balance equation, which would take the form ${\tilde{\mathit{M}}}^{(i)}+{\mathit{M}}_{\mathrm{elast}}^{(i)}+{\mathit{M}}_{\mathrm{motor}}^{(i)}=\mathbf{0}$, where now it is the moment M⁽ⁱ⁾_motor which has a fixed value. In what follows, we focus on the rotation-given problem, aiming to generalize the results predicted by the previous theoretical model [26]. The theoretical extension to the torque-given problem with N = 2 flagella is presented in appendix B where we highlight the similarities and differences between the two models.

(b). Identical and axisymmetric flagellar propulsion

From (2.4), (2.7) and (2.9), we obtain the governing equations in a matrix form

$$\mathcal{A}\left(\begin{array}{c}\mathit{U}\\ \mathit{\Omega }\\ {\mathit{\omega }}^{(i)}\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\\ -{\mathit{M}}_{\mathrm{elast}}^{(i)}\end{array}\right),$$ 2.12

where A is a square matrix of order 2N + 6, given by

$$\mathcal{A}=\left(\begin{array}{ccc}{C}_D\mathsf{1}+\sum _{i=1}^N{\int }_0^{L^{(i)}}{\mathsf{C}}_i\hspace{0.17em}\mathrm{d}s& \sum _{i=1}^N{\int }_0^{L^{(i)}}{\mathsf{C}}_i\cdot {\mathsf{A}}_i\hspace{0.17em}\mathrm{d}s& {\int }_0^{L^{(i)}}{\mathsf{C}}_i\cdot {\tilde{\mathsf{A}}}_i\hspace{0.17em}\mathrm{d}s\\ \sum _{i=1}^N{\int }_0^{L^{(i)}}{\mathsf{A}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\hspace{0.17em}\mathrm{d}s& C_R\mathsf{1}+\sum _{i=1}^N{\int }_0^{L^{(i)}}{\mathsf{A}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\mathsf{A}}_i\hspace{0.17em}\mathrm{d}s& {\int }_0^{L^{(i)}}{\mathsf{A}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\tilde{\mathsf{A}}}_i\hspace{0.17em}\mathrm{d}s\\ {\mathsf{P}}_i\cdot {\int }_0^{L^{(i)}}{\tilde{\mathsf{A}}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\hspace{0.17em}\mathrm{d}s& {\mathsf{P}}_i\cdot {\int }_0^{L^{(i)}}{\tilde{\mathsf{A}}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\mathsf{A}}_i\hspace{0.17em}\mathrm{d}s& {\mathsf{P}}_i\cdot {\int }_0^{L^{(i)}}{\tilde{\mathsf{A}}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\tilde{\mathsf{A}}}_i\hspace{0.17em}\mathrm{d}s\end{array}\right).$$ 2.13

We next decompose the flagellar rotation velocity vector into the components due to the flagellar rotation and that due to the flagellar bending, ω⁽ⁱ⁾ = ω⁽ⁱ⁾_t + ω⁽ⁱ⁾_n, with ω⁽ⁱ⁾_t = (ω⁽ⁱ⁾ · e⁽ⁱ⁾) e⁽ⁱ⁾. In the rotation-given problem, ω⁽ⁱ⁾_t = ω⁽ⁱ⁾ · e⁽ⁱ⁾ is a fixed value. For more convenience, we introduce 3 × 3 matrices to simplify the linear equations (2.12) as

$$\left(\begin{array}{ccc}{\mathsf{K}}_{TT}& {\mathsf{K}}_{TR}& {\mathsf{K}}_{TF}^{(i)}\\ {\mathsf{K}}_{RT}& {\mathsf{K}}_{RR}& {\mathsf{K}}_{RF}^{(i)}\\ {\mathsf{P}}_i\cdot {\mathsf{K}}_{FT}^{(i)}& {\mathsf{P}}_i\cdot {\mathsf{K}}_{FR}^{(i)}& {\mathsf{P}}_i\cdot {\mathsf{K}}_{FF}^{(i)}\end{array}\right)\left(\begin{array}{c}\mathit{U}\\ \mathit{\Omega }\\ {\mathit{\omega }}_n^{(i)}\end{array}\right)=\left(\begin{array}{c}-\sum _{i=1}^N{\mathsf{K}}_{TF}^{(i)}\cdot {\mathit{\omega }}_t^{(i)}\\ -\sum _{i=1}^N{\mathsf{K}}_{RF}^{(i)}\cdot {\mathit{\omega }}_t^{(i)}\\ -{\mathit{M}}_{\mathrm{elast}}^{(i)}-{\mathsf{P}}_i\cdot {\mathsf{K}}_{FF}^{(i)}\cdot {\mathit{\omega }}_t^{(i)}\end{array}\right).$$ 2.14

In order to proceed, we assume that all N flagella are identical and that they generate axisymmetric propulsion around their long axes. This assumption is obviously satisfied for axisymmetric flagellar shapes such as rods, but is also valid for asymmetric shapes, including helices, provided that the time scale of flagellar rotation is much smaller than that of elastic bending (i.e. |ω_t|≫|ω_n|). In practice, this assumption of axisymmetric propulsion is satisfied for swimming bacteria [30]. Indeed, the typical flagellar rotation frequency of flagellar filaments for E. coli is ≈100 Hz, which is faster than the typical frequency of cell rotation, ≈10 Hz. We can therefore approximate the propulsion by a rotating helical flagellar filament by its time-averaged contribution, which is axisymmetric along the helix axis.

We introduce a reference frame, flagellum-fixed frames and the rotation matrix, mapping the laboratory reference frame, {e_x, e_y, e_z}, onto the flagellum-fixed coordinates, {e⁽ⁱ⁾_x, e⁽ⁱ⁾_y, e⁽ⁱ⁾_z} and denoted by R_i, as schematically shown in figure 1. The axisymmetric conditions are satisfied if the quantity is unchanged under rotation around e⁽ⁱ⁾_z, where we choose the flagellum-fixed coordinates such that the z-axis (e⁽ⁱ⁾_z) coincides with e⁽ⁱ⁾ (see also figure 1).

For any second-rank tensor written in the reference-frame as K, its expression in the body-fixed frame, K_i, is given by

$$\mathsf{K}={\mathsf{R}}_i\cdot {\mathsf{K}}_i\cdot {\mathsf{R}}_i^{-1}.$$ 2.15

We next assume that the tensor is axisymmetric around the vector e⁽ⁱ⁾ = e⁽ⁱ⁾_z. This can be expressed by requiring invariance under rotation by any angle α∈[0, 2π) around the axis, i.e.

$$\mathsf{K}=\mathsf{R}(-\alpha ;{\mathit{e}}^{(i)})\cdot \mathsf{K}\cdot \mathsf{R}(\alpha ;{\mathit{e}}^{(i)}),$$ 2.16

where R(α;e⁽ⁱ⁾) denotes the rotation matrix of angle α around e⁽ⁱ⁾. If the tensor K_i is represented as a matrix, the axisymmetric property leads to the matrix form

$${\mathsf{K}}_i=\left(\begin{array}{ccc}{K}_{11}& K_{12}& 0\\ K_{21}& K_{22}& 0\\ 0& 0& K_{33}\end{array}\right),$$ 2.17

and the four upper-left entries can be decomposed into the symmetric and skew-symmetric parts

$$\left(\begin{array}{cc}{K}_{11}& K_{12}\\ K_{21}& K_{22}\end{array}\right)=\left(\begin{array}{cc}{K}_s& 0\\ 0& K_s\end{array}\right)+\left(\begin{array}{cc}0& K_{ss}\\ -K_{ss}& 0\end{array}\right),$$ 2.18

where K_s and K_ss are constants. From the matrix form in (2.17), note that we readily obtain the commutation relation

$${\mathsf{P}}_i\cdot \mathsf{K}=\mathsf{K}\cdot {\mathsf{P}}_i.$$ 2.19

The tensors ${\tilde{\mathsf{A}}}_i$ and C_i depend only on the flagellar shape and if the flagellum shape is axisymmetric, these tensors are also axisymmetric. As a result, the tensor ${\mathsf{K}}_{FF}^{(i)}=\int {\tilde{\mathsf{A}}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\tilde{\mathsf{A}}}_i\hspace{0.17em}\mathrm{d}s$ is found to be axisymmetric, since ${\mathsf{K}}_{FF}^{(i)}=\int \mathsf{R}(-\alpha ;{\mathit{e}}^{(i)})\cdot {\tilde{\mathsf{A}}}_i^{\mathrm{T}}\cdot {\mathsf{C}}_i\cdot {\tilde{\mathsf{A}}}_i\cdot \mathsf{R}(\alpha ;{\mathit{e}}^{(i)})\hspace{0.17em}\mathrm{d}s=\mathsf{R}(-\alpha ;{\mathit{e}}^{(i)})\cdot {\mathsf{K}}_{FF}^{(i)}\cdot \mathsf{R}(\alpha ;{\mathit{e}}^{(i)})$. If instead the flagellar filaments are not rigorously axisymmetric, notably if they are helical, then as long as the rotation velocity around their long axis is sufficiently large compared with the velocity scale during bending, we can approximately replace the second-rank tensors by their time-averages, and the same arguments thus follow.

Using the relation (2.19), equation (2.14) can be simplified to

$$\left(\begin{array}{ccc}{\mathsf{K}}_{TT}& {\mathsf{K}}_{TR}& {\mathsf{K}}_{TF}^{(i)}\\ {\mathsf{K}}_{RT}& {\mathsf{K}}_{RR}& {\mathsf{K}}_{RF}^{(i)}\\ {\mathsf{P}}_i\cdot {\mathsf{K}}_{FT}^{(i)}& {\mathsf{P}}_i\cdot {\mathsf{K}}_{FR}^{(i)}& {\mathsf{K}}_{FF}^{(i)}\end{array}\right)\left(\begin{array}{c}\mathit{U}\\ \mathit{\Omega }\\ {\mathit{\omega }}_n^{(i)}\end{array}\right)=\left(\begin{array}{c}-\sum _{i=1}^N{\mathsf{K}}_{TF}^{(i)}\cdot {\mathit{\omega }}_t^{(i)}\\ -\sum _{i=1}^N{\mathsf{K}}_{RF}^{(i)}\cdot {\mathit{\omega }}_t^{(i)}\\ -{\mathit{M}}_{\mathrm{elast}}^{(i)}\end{array}\right).$$ 2.20

Similar arguments for K⁽ⁱ⁾_FF enable us to show that the symmetric tensors K⁽ⁱ⁾_TF = K^(i)T_FT are also axisymmetric around the axis e⁽ⁱ⁾. However, the tensors K⁽ⁱ⁾_RF = K^(i)T_FR are not necessarily axisymmetric, since A_i are not axisymmetric except when each e⁽ⁱ⁾ is parallel to x⁽ⁱ⁾. We then decompose ${\mathsf{A}}_i={\mathsf{A}}_i^{\prime }+{\tilde{\mathsf{A}}}_i$. Noting that A′_i is independent of the flagellar shape, we rewrite as K⁽ⁱ⁾_RF = A′^T_i · K⁽ⁱ⁾_TF + K⁽ⁱ⁾_FF so that the tensors ${\tilde{\mathsf{A}}}_i$, K⁽ⁱ⁾_TF and K⁽ⁱ⁾_FF are axisymmetric around the vector e⁽ⁱ⁾. For convenience, we write A′^T_i · K⁽ⁱ⁾_TF = K′⁽ⁱ⁾_RF.

We next employ the assumption that all flagellar filaments have identical propulsion, which guarantees that the axisymmetric tensor, K, can be expressed as K = R_i · K⁽⁰⁾ · R⁻¹_i, where the tensor K⁽⁰⁾ is common to all filaments. We also write the rotation of the flagellar angular velocity in the flagellum-fixed frame as ${\mathit{\omega }}_t^{(i)}={\mathsf{R}}_i\cdot {\tilde{\mathit{\omega }}}_t^{(i)}$; here ${\tilde{\mathit{\omega }}}_t^{(i)}$ is parallel to e_z and we can thus write ${\tilde{\mathit{\omega }}}_t^{(i)}={\tilde{\omega }}_t^{(i)}{\mathit{e}}_z$, where the value of ${\tilde{\omega }}_t^{(i)}$ is prescribed. Similarly, the elastic torque in the flagellum-fixed frame is written as ${\mathit{M}}_{\mathrm{elast}}^{(i)}={\mathsf{R}}_i\cdot {\tilde{\mathit{M}}}_{\mathrm{elast}}^{(i)}$. Since both K⁽ⁱ⁾_TF and K⁽ⁱ⁾_FF are axisymmetric, we can rewrite the linear equations (2.20) as

$$\left(\begin{array}{ccc}{\mathsf{K}}_{TT}& {\mathsf{K}}_{TR}& {\mathsf{R}}_i\cdot {\mathsf{K}}_{TF}^{(0)}\\ {\mathsf{K}}_{RT}& {\mathsf{K}}_{RR}& {\mathsf{K}}_{RF}^{(i)}\cdot {\mathsf{R}}_i\\ {\mathsf{R}}_i\cdot {\mathsf{P}}_0\cdot {\mathsf{K}}_{FT}^{(0)}\cdot {\mathsf{R}}_i^{-1}& {\mathsf{P}}_i\cdot {\mathsf{K}}_{FR}^{(i)}& {\mathsf{R}}_i\cdot {\mathsf{K}}_{FF}^{(0)}\end{array}\right)\left(\begin{array}{c}\mathit{U}\\ \mathit{\Omega }\\ {\tilde{\mathit{\omega }}}_n^{(i)}\end{array}\right)=\left(\begin{array}{c}-\sum _{i=1}^N{\mathsf{R}}_i\cdot {\mathsf{K}}_{TF}^{(0)}\cdot {\tilde{\mathit{\omega }}}_t^{(i)}\\ -\sum _{i=1}^N({\mathsf{K}}_{RF}^{\mathrm{\prime }(i)}\cdot {\mathsf{R}}_i+{\mathsf{R}}_i\cdot {\mathsf{K}}_{FF}^{(0)})\cdot {\tilde{\mathit{\omega }}}_t^{(i)}\\ -{\mathsf{R}}_i\cdot {\tilde{\mathit{M}}}_{\mathrm{elast}}^{(i)}\end{array}\right),$$ 2.21

where P₀ is the projection onto the x–y plane, defined as P_i = R_i · P₀ · R⁻¹_i. With additional rotational matrix in the bottom N rows, this can be simplified to

$$\left(\begin{array}{ccc}{\mathsf{K}}_{TT}& {\mathsf{K}}_{TR}& {\mathsf{R}}_i\cdot {\mathsf{K}}_{TF}^{(0)}\\ {\mathsf{K}}_{RT}& {\mathsf{K}}_{RR}& {\mathsf{K}}_{RF}^{(i)}\cdot {\mathsf{R}}_i\\ {\mathsf{P}}_0\cdot {\mathsf{K}}_{FT}^{(0)}\cdot {\mathsf{R}}_i^{-1}& {\mathsf{P}}_0\cdot {\mathsf{R}}_i^{-1}\cdot {\mathsf{K}}_{FR}^{(i)}& {\mathsf{K}}_{FF}^{(0)}\end{array}\right)\left(\begin{array}{c}\mathit{U}\\ \mathit{\Omega }\\ {\tilde{\mathit{\omega }}}_n^{(i)}\end{array}\right)=\left(\begin{array}{c}-{\mathit{F}}_{\mathrm{prop}}\\ -{\mathit{M}}_{\mathrm{prop}}\\ -{\tilde{\mathit{M}}}_{\mathrm{elast}}^{(i)}\end{array}\right).$$ 2.22

Here, we have used the fact that P₀ commutes with K⁽⁰⁾_FT and ${\tilde{\mathsf{K}}}_{FR}^{(0)}$ and that ${\mathsf{P}}_0\cdot {\tilde{\mathit{\omega }}}_n^{(i)}={\tilde{\mathit{\omega }}}_n^{(i)}$. The first and second entries of the right-hand side of (2.22) give the effective force and torque for the entire body, corresponding to propulsive force and torques

$${\mathit{F}}_{\mathrm{prop}}=\left(\sum _{i=1}^N{\tilde{\omega }}_t^{(i)}{\mathsf{R}}_i\right)\cdot {\mathsf{K}}_{TF}^{(0)}\cdot {\mathit{e}}_z$$ 2.23

and

$${\mathit{M}}_{\mathrm{prop}}=\sum _{i=1}^N{\mathsf{K}}_{RF}^{\mathrm{\prime }(i)}\cdot {\mathit{\omega }}_t^{(i)}+\left(\sum _{i=1}^N{\tilde{\omega }}_t^{(i)}{\mathsf{R}}_i\right)\cdot {\mathsf{K}}_{FF}^{(0)}\cdot {\mathit{e}}_z.$$ 2.24

For a symmetric configuration such that $(\sum _{i=1}^N{\tilde{\omega }}_t^{(i)}{\mathsf{R}}_i)\cdot {\mathit{e}}_z=\mathbf{0}$, only the first term of M_prop contributes to the motion of the cell. If we further assume that the reference flagellar orientation is normal to the sphere surface, i.e. e⁽ⁱ⁾_z(t = 0) = n⁽ⁱ⁾, we readily obtain ${\tilde{\mathit{M}}}_{\mathrm{elast}}^{(i)}=\mathbf{0}$ and M_prop = 0. Therefore, we have stationary solutions satisfying $\mathit{U}=\mathit{\Omega }={\tilde{\mathit{\omega }}}_n^{(i)}=\mathbf{0}$ for the symmetric-filament configurations.

From the axisymmetric propulsion of the flagellar filaments and using (2.17)–(2.18), we may obtain the general form of the tensors

$${\mathsf{K}}_C^{(0)}=\left(\begin{array}{ccc}{k}_C& 0& 0\\ 0& k_C& 0\\ 0& 0& K_C\end{array}\right),{\mathsf{K}}_{TF}^{(0)}=\left(\begin{array}{ccc}{k}_D& k_T& 0\\ -k_T& k_D& 0\\ 0& 0& K_T\end{array}\right),{\mathsf{K}}_{FF}^{(0)}=\left(\begin{array}{ccc}{k}_F& 0& 0\\ 0& k_F& 0\\ 0& 0& K_F\end{array}\right),$$ 2.25

where the constants, k_C, K_C, k_T, k_F, are all negative due to the negative definiteness of the Stokes resistance tensors and K_T and K_F are taken to be negative so that a positive value of ${\tilde{\omega }}_t$ generates flagellar force towards the cell body (as is the case for the majority of flagellated bacteria). From the definitions of K⁽⁰⁾_C and K⁽⁰⁾_FF, these matrices are symmetric, thus the expressions in (2.25) follow. The expression for K⁽⁰⁾_TF reflects the skew-symmetric property of Ã_i, and thus the diagonal component, k_D, is typically very small for swimming bacteria. The diagonal component of the matrix can be either positive or negative depending on the chirality of flagellar filaments. Using the appendix in [30], k_D can be estimated for a helical flagellum as k_D∼C_NbLϵ with b is the diameter of the helix and ϵ = 2πb/λ, where λ is the pitch of the helix. The ratio of diagonal to off-diagonal component is thus given by k_D/k_T∼ϵ(b/L)∼10⁻², always a small number for a bacterium such as E. coli [30]. Note that k_D is identically zero for rod-like flagella.

We now proceed with the linear stability problem neglecting chirality effects (i.e. setting k_D = 0) and will then incorporate chirality back in §5.

(c). Linear stability

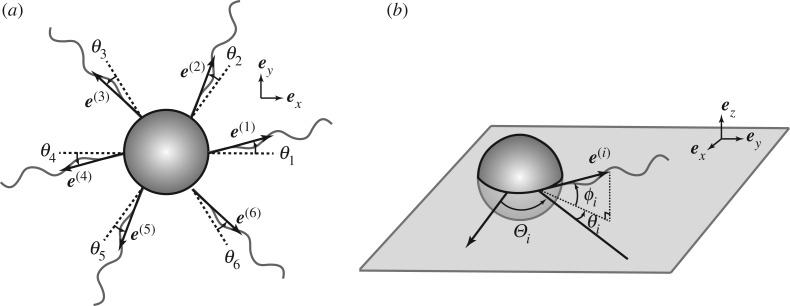
In this section, we assume the in-plane flagellar configuration is that of a regular polygon, and then formulate the linear stability problem around the equilibrium. The example case of N = 6 is schematically shown in figure 2a with notation. As shown above, with a symmetric flagellar configuration we obtain stationary solutions for the motion of a bacterium with N(≥2) identical axisymmetric flagella. We assume that the angular rotations of each flagellum, ω⁽ⁱ⁾_t, are identical and that each flagellar filament is connected perpendicularly to the cell body surface and located in one plane that we define as x–y plane (figure 2a). When the flagellar configuration forms an N-sided regular polygon, the bacterial motion is found to be stationary.

Figure 2.

(a) Schematic of a model bacterium with N identical flagella symmetrically attached in the x–y plane. (b) Angles specifying the orientation of a flagellum. The equilibrium orientation of ith flagellum is given by the rotation of angle Θ_i from the +x-axis. Small deformations from the equilibrium are measured by the two angles, θ_i and ϕ_i, which correspond to the in-plane and out-of-plane angles, respectively.

We now consider the linear stability around this equilibrium, where the orientation of ith flagellum is given by rotation of angle Θ_i from the +x-axis in the x–y plane where Θ_i = 2π(i − 1)/N (figure 2b). The disturbance from the equilibrium is denoted by two angles for each flagellum. We introduce the in-plane and out-of-plane angular displacements for the ith flagellum as θ_i and ϕ_i, as shown in figure 2a,b. In the linear stability regime, both angles are assumed to be sufficiently small, i.e. |θ_i|, |ϕ_i|≪1. We write the flagellar bending rotation as ${\tilde{\mathit{\omega }}}_n^{(i)}=(\mathrm{d}{\theta }_i/\mathrm{d}t)\hspace{0.17em}{\mathit{e}}_x^{(i)}+(\mathrm{d}{\varphi }_i/\mathrm{d}t)\hspace{0.17em}{\mathit{e}}_y^{(i)}$, assume a constant flagellar rotation around the axisymmetric axis, ${\tilde{\mathit{\omega }}}_t^{(i)}={\omega }_0$, and also assume that the torque spring constants are identical for all flagella, i.e. κ⁽ⁱ⁾ = κ.

We then proceed to obtain the expressions for the cell dynamics around the equilibrium configuration. The rotation matrix, R_i is obtained by combining the two rotations

$$\begin{array}{rl}{\mathsf{R}}_i& =\mathsf{R}({\varphi }_i;{\mathit{e}}_y)\cdot \mathsf{R}({\mathit{\Theta }}_i+{\theta }_i;{\mathit{e}}_x)\cdot \left(\begin{array}{ccc}0& 0& 1\\ 0& -1& 0\\ 1& 0& 0\end{array}\right)\\ & \simeq \left(\begin{array}{ccc}0& \sin {\mathit{\Theta }}_i& \cos {\mathit{\Theta }}_i\\ 0& -\cos {\mathit{\Theta }}_i& \sin {\mathit{\Theta }}_i\\ 1& 0& 0\end{array}\right)+{\theta }_i\left(\begin{array}{ccc}0& \cos {\mathit{\Theta }}_i& -\sin {\mathit{\Theta }}_i\\ 0& \sin {\mathit{\Theta }}_i& \cos {\mathit{\Theta }}_i\\ 0& 0& 0\end{array}\right)+{\varphi }_i\left(\begin{array}{ccc}-\cos {\mathit{\Theta }}_i& 0& 0\\ -\sin {\mathit{\Theta }}_i& 0& 0\\ 0& 0& 1\end{array}\right),\end{array}$$ 2.26

where R(ϕ_i;e_y) denotes the rotation matrix with angle ϕ_i around the orientation e_y. Using the expressions (2.25), we directly obtain the effective force

$$\begin{array}{rl}{\mathit{F}}_{\mathrm{prop}}& =\left(\sum _{i=1}^N{\omega }_0{\mathsf{R}}_i\right)\cdot {\mathsf{K}}_{TF}^{(0)}\cdot {\mathit{e}}_z={\omega }_0{K}_T(-\sum _{i=1}^N{\theta }_i\sin {\mathit{\Theta }}_i{\mathit{e}}_x+\sum _{i=1}^N{\theta }_i\cos {\mathit{\Theta }}_i{\mathit{e}}_y+\sum _{i=1}^N{\varphi }_i{\mathit{e}}_z),\end{array}$$ 2.27

and similarly the effective torque

$$\begin{array}{rl}{\mathit{M}}_{\mathrm{prop}}& ={\omega }_0{K}_T(\sum _{i=1}^N{\varphi }_i\sin {\mathit{\Theta }}_i{\mathit{e}}_x-\sum _{i=1}^N{\varphi }_i\cos {\mathit{\Theta }}_i{\mathit{e}}_y+\sum _{i=1}^N{\theta }_i{\mathit{e}}_z)\\ & +{\omega }_0{K}_F(-\sum _{i=1}^N{\theta }_i\sin {\mathit{\Theta }}_i{\mathit{e}}_x+\sum _{i=1}^N{\theta }_i\cos {\mathit{\Theta }}_i{\mathit{e}}_y+\sum _{i=1}^N{\varphi }_i{\mathit{e}}_z).\end{array}$$ 2.28

We then proceed to compute the force and torque generated by the in-plane flagellar bending, ${\tilde{\mathit{\omega }}}_n^{(i)}=(\mathrm{d}{\theta }_i/\mathrm{d}t){\mathit{e}}_x$. The force generated by each flagellar filament is ${\mathsf{R}}_i\cdot {\mathsf{K}}_{TF}^{(0)}\cdot {\tilde{\mathit{\omega }}}_n^{(i)}\simeq k_T(\mathrm{d}{\theta }_i/\mathrm{d}t)(-\sin {\mathit{\Theta }}_i{\mathit{e}}_x+\cos {\mathit{\Theta }}_i{\mathit{e}}_y)$. Similarly, the torque generated can also be computed, using the decomposition ${\mathsf{K}}_{RF}^{(i)}\cdot {\mathsf{R}}_i\cdot {\tilde{\mathit{\omega }}}_n^{(i)}=({\mathsf{A}}_i^{\mathrm{\prime }\mathrm{T}}\cdot {\mathsf{R}}_i\cdot {\mathsf{K}}_{TF}^{(0)}+{\mathsf{R}}_i\cdot {\mathsf{K}}_{FF}^{(0)})\cdot {\tilde{\mathit{\omega }}}_n^{(i)}=(k_T+k_F)(\mathrm{d}{\theta }_i/\mathrm{d}t){\mathit{e}}_z$.

The force generated by the out-of-plane flagellar bending, ${\tilde{\omega }}_n^{(i)}=(\mathrm{d}{\varphi }_i/\mathrm{d}t){\mathit{e}}_y$, is also computed as R_i · K⁽⁰⁾_TF · (dϕ_i/dt)e_y = k_T(dϕ_i/dt)R_i · e_x≃k_T(dϕ_i/dt)e_z. Similarly, we obtain the torque generated by the bending, (dϕ_i/dt)e_y, as K⁽ⁱ⁾_RF · R_i · (dϕ_i/dt)e_y = (dϕ_i/dt)(A′^T_i · R_i · K⁽⁰⁾_TF + R_i · K⁽⁰⁾_FF) · e_y = (dϕ_i/dt)(k_TA′^T_i · R_i · e_x + k_FR_i · e_y) = (dϕ_i/dt)(k_T + k_F)(sinΘ_ie_x − cosΘ_ie_y).

A lengthy but straightforward calculation then leads to the matrix expression for the motion around the equilibrium, captured by a 2N + 6-dimensional linear problem

$$\mathcal{A}\mathbf{\Phi }=\mathit{b},$$ 2.29

where $\mathbf{\Phi }={(U_x,U_y,U_z,{\mathit{\Omega }}_x,{\mathit{\Omega }}_y,{\mathit{\Omega }}_z,{\dot{\theta }}_1,\dots ,{\dot{\theta }}_N,{\dot{\varphi }}_1,\dots ,{\dot{\varphi }}_N)}^{\mathrm{T}}$ and

$$\mathit{b}={(-{\mathit{F}}_{\mathrm{prop}}^{\mathrm{T}},-{\mathit{M}}_{\mathrm{prop}}^{\mathrm{T}},\kappa {\theta }_1,\dots ,\kappa {\theta }_N,\kappa {\varphi }_1,\dots ,\kappa {\varphi }_N)}^{\mathrm{T}}.$$ 2.30

The detailed derivations leading to the expressions for the square matrix $\mathcal{A}$ can be found in appendix A and the results are

$$\mathcal{A}=\left(\begin{array}{cccccccc}{C}_{D1}& 0& 0& 0& 0& 0& {\mathit{C}}_{TF1}^{\mathrm{T}}& \mathbf{0}\\ 0& C_{D2}& 0& 0& 0& 0& {\mathit{C}}_{TF2}^{\mathrm{T}}& \mathbf{0}\\ 0& 0& C_{D3}& 0& 0& 0& \mathbf{0}& {\mathit{C}}_{TF3}^{\mathrm{T}}\\ 0& 0& 0& C_{R1}& 0& 0& \mathbf{0}& {\mathit{C}}_{RF1}^{\mathrm{T}}\\ 0& 0& 0& 0& C_{R2}& 0& \mathbf{0}& {\mathit{C}}_{RF2}^{\mathrm{T}}\\ 0& 0& 0& 0& 0& C_{R3}& {\mathit{C}}_{RF3}^{\mathrm{T}}& \mathbf{0}\\ {\mathit{C}}_{TF1}& {\mathit{C}}_{TF2}& \mathbf{0}& \mathbf{0}& \mathbf{0}& {\mathit{C}}_{RF3}& k_F{\mathbf{1}}_N& {\mathbf{0}}_N\\ \mathbf{0}& \mathbf{0}& {\mathit{C}}_{TF3}& {\mathit{C}}_{RF1}& {\mathit{C}}_{RF2}& \mathbf{0}& {\mathbf{0}}_N& k_F{\mathbf{1}}_N\end{array}\right),$$ 2.31

where the constants in the matrix are

$$\begin{array}{r}{C}_{D1}=C_D+\sum _{i=1}^N(K_C{\cos }^2{\mathit{\Theta }}_i+k_C{\sin }^2{\mathit{\Theta }}_i),\end{array}$$ 2.32

$$\begin{array}{r}{C}_{D2}=C_D+\sum _{i=1}^N(K_C{\sin }^2{\mathit{\Theta }}_i+k_C{\cos }^2{\mathit{\Theta }}_i),\end{array}$$ 2.33

$$\begin{array}{r}{C}_{D3}=C_D+N{k}_C,\end{array}$$ 2.34

$$\begin{array}{r}{C}_{R1}=C_R+\sum _{i=1}^N((k_C+2k_T+k_F){\sin }^2{\mathit{\Theta }}_i+K_F{\cos }^2{\mathit{\Theta }}_i),\end{array}$$ 2.35

$$\begin{array}{r}{C}_{R2}=C_R+\sum _{i=1}^N((k_C+2k_T+k_F){\cos }^2{\mathit{\Theta }}_i+K_F{\sin }^2{\mathit{\Theta }}_i)\end{array}$$ 2.36

$$\begin{array}{rl}\mathrm{and}& C_{R3}=C_R+N(k_C+2k_T+k_F),\end{array}$$ 2.37

and the N-dimensional vectors are given by

$$\begin{array}{r}{\mathit{C}}_{TF1}=-k_T{(\sin {\mathit{\Theta }}_1,\dots ,-\sin {\mathit{\Theta }}_N)}^{\mathrm{T}},{\mathit{C}}_{RF1}=(k_T+k_F){(\sin {\mathit{\Theta }}_1,\dots ,\sin {\mathit{\Theta }}_N)}^{\mathrm{T}},\end{array}$$ 2.38

$$\begin{array}{r}{\mathit{C}}_{TF2}=k_T{(\cos {\mathit{\Theta }}_1,\dots ,\cos {\mathit{\Theta }}_N)}^{\mathrm{T}},{\mathit{C}}_{RF2}=-(k_T+k_F){(\cos {\mathit{\Theta }}_1,\dots ,\cos {\mathit{\Theta }}_N)}^{\mathrm{T}}\end{array}$$ 2.39

$$\begin{array}{rl}\mathrm{and}& {\mathit{C}}_{TF3}={(k_T,\dots ,k_T)}^{\mathrm{T}},{\mathit{C}}_{RF3}={(k_T+k_F,\dots ,k_T+k_F)}^{\mathrm{T}},\end{array}$$ 2.40

and we used 1_N and 0_N to denote the identity and zero matrices of order N. In the following sections, we will consider the stability of this linear system.

3. Instability of bacteria with N = 2 flagella

We start with analysing the N = 2 case. Substituting N = 2 in the expressions (2.29)–(2.31), we obtain a 10-dimensional linear system (figure 3). With the geometric symmetry of the system, we readily find that the x-component of the effective force and torque vanish and thus U_x = Ω_x = 0 follow. The system is then reduced to an eight-dimensional linear system. Introducing the variables θ + = θ₁ + θ₂, θ − = θ₁ − θ₂, ϕ + = ϕ₁ + ϕ₂ and ϕ − = ϕ₁ − ϕ₂, we can rewrite the linear system (2.29) into four blocks of 2 × 2 matrices as

$$\begin{array}{rl}& \left(\begin{array}{cc}{C}_D^{\prime }& k_T\\ 2k_T& k_F\end{array}\right)\left(\begin{array}{c}{U}_y\\ {\dot{\theta }}_{-}\end{array}\right)=\left(\begin{array}{c}-{\omega }_0{K}_T{\theta }_{-}\\ \kappa {\theta }_{-}\end{array}\right),\end{array}$$ 3.1

$$\begin{array}{rl}& \left(\begin{array}{cc}{C}_D^{\prime }& k_T\\ 2k_T& k_F\end{array}\right)\left(\begin{array}{c}{U}_z\\ {\dot{\varphi }}_{+}\end{array}\right)=\left(\begin{array}{c}-{\omega }_0{K}_T{\varphi }_{+}\\ \kappa {\varphi }_{+}\end{array}\right),\end{array}$$ 3.2

$$\begin{array}{rl}& \left(\begin{array}{cc}{C}_R^{\prime }& -(k_T+k_F)\\ -2(k_T+k_F)& k_F\end{array}\right)\left(\begin{array}{c}{\mathit{\Omega }}_y\\ {\dot{\varphi }}_{-}\end{array}\right)=\left(\begin{array}{c}{\omega }_0{K}_T{\varphi }_{-}-{\omega }_0{K}_F{\theta }_{-}\\ \kappa {\varphi }_{-}\end{array}\right)\end{array}$$ 3.3

$$\begin{array}{rl}\mathrm{and}& \left(\begin{array}{cc}{C}_R^{\prime }& k_T+k_F\\ 2(k_T+k_F)& k_F\end{array}\right)\left(\begin{array}{c}{\mathit{\Omega }}_z\\ {\dot{\theta }}_{+}\end{array}\right)=\left(\begin{array}{c}-{\omega }_0{K}_T{\theta }_{+}-{\omega }_0{K}_F{\varphi }_{+}\\ \kappa {\theta }_{+}\end{array}\right),\end{array}$$ 3.4

where we have defined C_D′ = C_D + 2k_C and C_R′ = C_R + 2k_C + 4k_T + 2k_F and where the dot symbol indicates the time derivative of the angle variable.

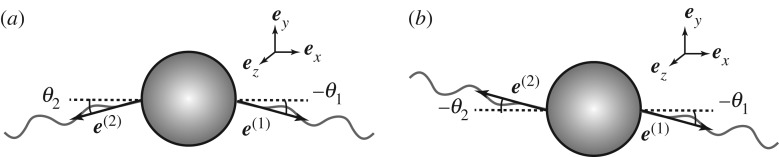
Figure 3.

Schematic pictures of the two modes of flagellar configuration for the N = 2 case. (a) Translation mode when the two flagella are in a mirror-symmetric configuration. (b) Rotation mode when the two flagella are in a point-symmetric configuration.

Solving each two-dimensional problem yields ordinary differential equations with respect to the four angle variables as

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}{\theta }_{+}\\ {\varphi }_{+}\\ {\varphi }_{-}\\ {\theta }_{-}\end{array}\right)=\left(\begin{array}{cccc}{A}_R& A_{RT}& 0& 0\\ 0& A_T& 0& 0\\ 0& 0& A_R& -A_{RT}\\ 0& A_T\end{array}\right)\left(\begin{array}{c}{\theta }_{+}\\ {\varphi }_{+}\\ {\varphi }_{-}\\ {\theta }_{-}\end{array}\right),$$ 3.5

where the expressions for A_T, A_R, A_RT are given by

$$\begin{array}{rl}& A_T={\mathrm{\Delta }}_D^{-1}(2{\omega }_0|K_T{k}_T|-\kappa |C_D^{\prime }|),\end{array}$$ 3.6

$$\begin{array}{r}\\ & A_R={\mathrm{\Delta }}_R^{-1}(2{\omega }_0|K_T(k_T+k_F)-\kappa |C_R^{\prime }|)\end{array}$$ 3.7

$$\begin{array}{rl}\mathrm{and}& A_{RT}={\mathrm{\Delta }}_R^{-1}(2{\omega }_0|K_F(k_T+k_F)|,\end{array}$$ 3.8

and where the two determinants, Δ_D = C_D′k_F − 2k²_F and Δ_R = C_R′k_F − 2(k_T + k_F)², are positive as a result of the negative-definiteness of the Stokes resistance matrices.

We first consider the simple case with K_F = 0 where the flagellar filaments produce propulsion but no torque. This assumption follows for a rod-like active filament as in [26]. Under this assumption, the matrix (3.5) is diagonal, since A_RT = 0 and with eigenvalues A_T and A_R. The angles θ − and ϕ + correspond to the translation modes in the y- and z-directions, respectively (figure 3a). The critical flagellar angular velocity, ω_0T, above which the translation mode becomes unstable is given by

$${\omega }_{0T}=\frac{|C_D+2k_C|}{2|K_T{k}_T|}\kappa ,$$ 3.9

which is positive. When ω₀ > 0, the flagellar filaments exert propulsive forces pushing on the cell body, whereas they pull on the organism when ω₀ < 0. We therefore obtain that the translation instability only occurs for flagellar filaments in the pushing mode and with sufficiently large propulsive magnitude (or, for a fixed propulsion, with a sufficiently flexible hook). This can be compared to the arguments put forward in [26], where the force by a rod-like flagellum corresponds to the product ω₀K_T. Note that here the translation can occur towards an arbitrary direction in the y–z-plane.

The eigenvectors corresponding to the eigenvalue A_R are linear combinations of the angles θ + and ϕ − and characterize a rotation mode around z- and y-axes, respectively (figure 3b). Although the rotation mode has not been examined in [26] (that study assumed mirror-image symmetry in their theoretical description), the rotation instability can occur above a second critical flagellar angular velocity, ω_0R, given by

$${\omega }_{0R}=\frac{|C_R+2k_C+4k_T+2k_F|}{2|K_T(k_T+k_F)|}\kappa .$$ 3.10

Note that this critical value is positive and therefore the rotation instability also occurs only for flagellar filaments in the pushing mode.

In the case where K_F≠0, each flagellar filament generates both torque and force. Again, we obtain the same eigenvalues of the matrix, A_R, A_T, as in the problem of the flagella without torque generation. Moreover, the eigenvectors associated with the eigenvalue A_R are the same as above (pure rotation move). As a difference, however, the eigenvectors for the eigenvalue A_T are combinations of the four angles and the induced motion is found to be a translation in y–z-plane combined with a rotation around the translation direction. This unstable mode corresponds to the case of bacterial flagellar bundling via the elastohydrodynamic instability as observed experimentally and reproduced using numerical simulations in [26].

(a). Most unstable mode

When the angular velocity of each flagellar filament is positive, the two modes can become unstable. However, only the most unstable mode from the linear stability theory is likely to be observed in practice and we now consider which one of the two modes becomes unstable first.

Let us denote the length of the identical flagella by L. Using dimensional analysis allows to obtain order-of-magnitude estimates for the dependence with L of the constants from the flagellar shape, namely k_C = O(L), k_T = O(L²) and k_F = O(L³). Noting that C_D = − 6π and C_R = − 8π, we can then estimate the size of the ratio r between the two critical angular velocities, r≡ω_0T/ω_0R, as r∼C_D/C_R = 3/4 when L≪1 and r = O(L⁻¹) when L≫1. In both limits, we see that the critical value for the translation instability is smaller, and thus it is the one which would be observed.

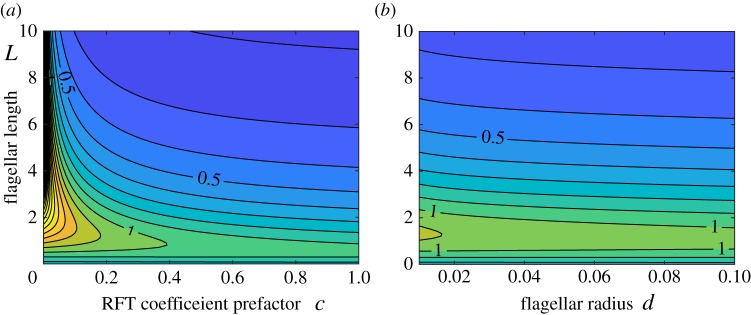
For further discussions in the intermediate region of L, we consider rod-like flagellar filaments of radius d and length L. We introduce a positive constant c such that C_n = − 4πμc is the normal drag coefficient, c is given by c = (log(2L/d) + 0.5)⁻¹ [28]. Within resistive force theory, the coefficients are given by k_C = C_nL, k_T = (C_n/2)L² and k_F = (C_n/3)L³ and we can compute numerically the ratio r for different flagellar parameters, c and L, or d and L, with results plotted in figure 4.

Figure 4.

Ratio between the two values of angular velocities for the translation and rotation modes, r = ω_0T/ω_0R, as a function of flagellar parameters. (a) Iso-values of r as a function of the RFT coefficient prefactor c and the flagellar length L. (b) Iso-values of r as a function of flagellar radius d and the flagellar length L. (Online version in colour.)

In figure 4a, iso-values of the frequency ratio r is first shown for different values c and L and we find that in the intermediate region L∼1 the rotation mode can be more unstable, although the translational mode is always more unstable above a critical value of c ≈ 0.4. The same plot is then shown with the flagellar radius d in the horizontal axis of figure 4b, indicating that the rotation instability would occur first in a robust range of flagellar radius if L∼1.

Typical sizes of the cell body and the flagellar filaments of E. coli are ≈1 mm and ≈10 mm [28], leading to a large non-dimensional flagellar length, L ≈ 10, and thus the translation mode is predicted to be the experimentally observable one. Similarly, the typical size of the dimensionless flagellar radius and the RFT coefficient prefactor are given by d ≈ 0.02 and c ≈ 0.13, respectively, and a cell equipped with short flagellar filaments could therefore, in theory, undergo the rotational instability without net locomotion.

We next consider a helical flagellum whose shape is characterized by the helix angle Ψ between the local flagellar tangent vector, t⁽ⁱ⁾ and the axis of the helix, e⁽ⁱ⁾_z. The tangent vector can be expressed by t⁽ⁱ⁾ = cosΨe⁽ⁱ⁾_z + sinΨ( − sinβe⁽ⁱ⁾_x + cosβe⁽ⁱ⁾_y) with the angle β in the range β∈[0, 2π). For the flagellar filament moved along the e⁽ⁱ⁾_x-axis with velocity u, direct computations from (2.1) gives the local drag force

$$\mathrm{d}\mathit{F}\cdot {\mathit{e}}_x^{(i)}=C_n[1-(1-\gamma ){\sin }^2\mathit{\Psi }{\sin }^2\beta ]u,$$ 3.11

where γ = C_t/C_n is the ratio of the tangential and normal coefficients from resistive force theory. If the time scale of flagellar rotation is sufficiently faster than that of bending, we can approximate the local force by its time-averaged value, which is obtained averaging over the angle parameter β. We thus obtain dF · e⁽ⁱ⁾_x = C′_nu, with the effective normal drag coefficient C′_n = − 4πμc′ as

$$C_n^{\prime }=[1-\frac{1}{2}(1-\gamma ){\sin }^2\mathit{\Psi }]C_n,$$ 3.12

enabling us to follow the same arguments for the rod-like flagella by simply replacing C_n by C′_n, or c by c′. Typical values of γ and Ψ for E. coli are γ ≈ 0.7 [31] and Ψ ≈ 30° [23], resulting in the effective drag coefficient, and thus the effective value of c, to be similar to the case of a rod (c′ ≈ 0.13). As before, the translation mode is therefore more unstable for a bacterium with typical experimental sizes, though there is a region where the rotation mode can be more unstable when L∼1. Note however that this assumes that the helical structure of the filament is neglected, a modelling assumption which is corrected in §5.

4. Instability of bacteria with N≥3 flagella

We now proceed to study the linear stability problem in the general case of N flagellar filaments. When N≥3, the drag coefficients (2.32)–(2.37) can be simplified to

$$C_{D1}=C_{D2}=C_D+\left(\frac{N}{2}\right)(K_C+k_C),C_{D3}=C_D+N{k}_C,$$ 4.1

and

$$C_{R1}=C_{R2}=C_R+\left(\frac{N}{2}\right)(k_C+2k_T+k_F+K_F),C_{R3}=C_R+N(k_C+2k_T+k_F),$$ 4.2

where we have used the equalities

$$\sum _{i=1}^N{\cos }^2\left(\frac{2\pi (i-1)}{N}\right)=\sum _{i=1}^N{\sin }^2\left(\frac{2\pi (i-1)}{N}\right)=\frac{N}{2},$$ 4.3

which are satisfied when N≥3. We first address the N = 3 and N = 4 cases to allow for intuition on the mathematical structure of the solution, before proceeding to the general N case.

(a). Cell with N = 3 flagella

When N = 3, the number of the angular variables is 6, which is equal to the number of degrees of freedom for the rigid motion of the whole cell. As in the previous section, we partially diagonalize the matrix (2.31) by introducing the angle variables, ${\tilde{\theta }}_1={\theta }_2-{\theta }_3$, ${\tilde{\theta }}_2=2{\theta }_1-{\theta }_2-{\theta }_3$ and ${\tilde{\theta }}_3={\theta }_1+{\theta }_2+{\theta }_3$ for the in-plane angles and ${\tilde{\varphi }}_1={\varphi }_2-{\varphi }_3$, ${\tilde{\varphi }}_2=2{\varphi }_1-{\varphi }_2-{\varphi }_3$ and ${\tilde{\varphi }}_3={\varphi }_1+{\varphi }_2+{\varphi }_3$ for the out-of-plane angles.

We then obtain a linear system decomposed into 6 two-by-two block matrices in which one degree of freedom for rigid motion is paired with an angle variable. For the translation and rotation in x-direction, the matrices are given by

$$\left(\begin{array}{cc}{C}_{D1}& -\frac{\sqrt{3}}{2}{k}_T\\ -\sqrt{3}{k}_T& k_F\end{array}\right)\left(\begin{array}{c}{U}_x\\ {\dot{\tilde{\theta }}}_1\end{array}\right)=\left(\begin{array}{c}\frac{\sqrt{3}}{2}{\omega }_0{K}_T{\tilde{\theta }}_1\\ \kappa {\tilde{\theta }}_1\end{array}\right)$$ 4.4

and

$$\left(\begin{array}{cc}{C}_{R1}& -\frac{\sqrt{3}}{2}(k_T+k_F)\\ -\sqrt{3}(k_T+k_F)& k_F\end{array}\right)\left(\begin{array}{c}{\mathit{\Omega }}_x\\ {\dot{\tilde{\varphi }}}_1\end{array}\right)=\left(\begin{array}{c}\frac{\sqrt{3}}{2}{\omega }_0(K_F{\tilde{\theta }}_1-K_T{\tilde{\varphi }}_1)\\ \kappa {\tilde{\varphi }}_1\end{array}\right),$$ 4.5

from which we obtain the ordinary differential equations for the linear stability in the form

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}{\tilde{\theta }}_1\\ {\tilde{\varphi }}_1\end{array}\right)=\left(\begin{array}{cc}{A}_T& 0\\ A_{TR3}& A_{R3}\end{array}\right)\left(\begin{array}{c}{\tilde{\theta }}_1\\ {\tilde{\varphi }}_1\end{array}\right),$$ 4.6

where A_T = Δ⁻¹_T((3/2)|K_Tk_T|ω₀ − |C_D1|κ), A_R3 = Δ⁻¹_R3((3/2)|K_T(k_T + k_F)|ω₀ − |C_R1|κ) and A_TR3 = (3/2)Δ⁻¹_R3|K_F(k_T + k_F)|ω₀, with the determinants Δ_T = C_D1k_F − (3/2)k²_T and Δ_R3 = C_R1k_F − (3/2)(k_T + k_F)². From (4.6), we can read off directly the eigenvalues for the linear stability with the rigid motion in x-direction as A_T and A_R3. The eigenvectors are pure rotation around the x-axis (A_R3 eigenvalue) and translation along the x-axis accompanied by rotation around the x-axis (A_T).

In a similar manner, we can derive the eigenvalues for linear stability associated with the rigid motion in the y-direction. Noting that C_D1 = C_D2 and C_R1 = C_R2, we obtain an equation similar to (4.6)

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}{\tilde{\theta }}_2\\ {\tilde{\varphi }}_2\end{array}\right)=\left(\begin{array}{cc}{A}_T& 0\\ A_{TR3}& A_{R3}\end{array}\right)\left(\begin{array}{c}{\tilde{\theta }}_2\\ {\tilde{\varphi }}_2\end{array}\right),$$ 4.7

which yields the same eigenvalues A_T and A_R3 as in the linear stability in x-direction.

For the translation and rotation in the z-direction, the matrices are now given by

$$\left(\begin{array}{cc}{C}_{D3}& -k_T\\ -k_T& k_F\end{array}\right)\left(\begin{array}{c}{U}_z\\ {\dot{\tilde{\varphi }}}_3\end{array}\right)=\left(\begin{array}{c}-{\omega }_0{K}_T{\tilde{\varphi }}_3\\ \kappa {\tilde{\varphi }}_3\end{array}\right)$$ 4.8

and

$$\left(\begin{array}{cc}{C}_{R3}& k_T+k_F\\ 3(k_T+k_F)& k_F\end{array}\right)\left(\begin{array}{c}{\mathit{\Omega }}_z\\ {\dot{\tilde{\theta }}}_3\end{array}\right)=\left(\begin{array}{c}-{\omega }_0(K_F{\tilde{\varphi }}_3-K_T{\tilde{\theta }}_3)\\ \kappa {\tilde{\theta }}_3\end{array}\right),$$ 4.9

yielding the equation for the linear stability,

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}{\tilde{\varphi }}_3\\ {\tilde{\theta }}_3\end{array}\right)=\left(\begin{array}{cc}{A}_{T3}& 0\\ -A_{RT3}& A_R\end{array}\right)\left(\begin{array}{c}{\tilde{\varphi }}_3\\ {\tilde{\theta }}_3\end{array}\right),$$ 4.10

where A_T3 = Δ⁻¹_T3(3|K_Tk_T|ω₀ − |C_D3|κ), A_R3 = Δ⁻¹_R(3|K_T(k_T + k_F)|ω₀ − |C_R1|κ) and A_TR3 = 3Δ⁻¹_R|K_F(k_T + k_F)|ω₀, with the determinants Δ_T3 = C_D3k_F − 3k²_T and Δ_R = C_R3k_F − 3(k_T + k_F)². The system in (4.10) provides the eigenvalues of the linear stability associated with the rigid motion in z-direction as A_R and A_T3, with corresponding eigenvectors of pure rotation around the z-axis and combined translation and rotation along the z-axis, respectively.

In summary, we obtain six eigenvalues, A_T, A_T, A_T3, A_R, A_R3, A_R3, each of which is accompanied by a rigid-motion mode for the whole cell.

(b). Cell with N = 4 flagella

In the case of a cell equipped with N = 4 flagella, the number of angle variables exceeds the numbers of degrees of freedom for a rigid-body motion of the cell body. We again introduce new angle variables to decompose the square matrix of order 2N + 6 into smaller size systems as ${\tilde{\theta }}_1={\theta }_2-{\theta }_4$, ${\tilde{\theta }}_2={\theta }_1-{\theta }_3$, ${\tilde{\theta }}_3={\theta }_1+{\theta }_2+{\theta }_3$ and ${\tilde{\theta }}_4={\theta }_1-{\theta }_2+{\theta }_3-{\theta }_4$, with similar combinations for the out-of-plane angle variables. From these changes of variables, we obtain the six matrices associated with the rigid motion and the angle variables, ${\tilde{\theta }}_i$ and ${\tilde{\varphi }}_i$ for i = 1, 2, 3. In turn, we obtain the same form of the linear ordinary differential equations for the linear stability as of (4.6), (4.7) and (4.10), for the x-, y- and z-directions, respectively. However, the values of the matrix entries are now given by A_T = Δ⁻¹_T(2|K_Tk_T|ω₀ − |C_D1|κ), A_R3 = Δ⁻¹_R3(2|K_T(k_T + k_F)|ω₀ − |C_R1|κ) and A_TR3 = (2Δ⁻¹_R3|K_F(k_T + k_F)|ω₀, with the determinants Δ_T = C_D1k_F − 2k²_T and Δ_R3 = C_R1k_F − 2(k_T + k_F)² for the instabilities in x- and y-directions and A_T3 = Δ⁻¹_T3(4|K_Tk_T|ω₀ − |C_D3|κ), A_R3 = Δ⁻¹_R(4|K_T(k_T + k_F)|ω₀ − |C_R1|κ) and A_TR3 = 4Δ⁻¹_R|K_F(k_T + k_F)|ω₀, with the determinants Δ_T3 = C_D3k_F − 4k²_T and Δ_R = C_R3k_F − 4(k_T + k_F)² for the instability in the z-direction.

The remaining two angular degrees of freedom are diagonalized as

$$\left(\begin{array}{cc}{k}_F& 0\\ 0& k_F\end{array}\right)\left(\begin{array}{c}{\dot{\tilde{\theta }}}_4\\ {\dot{\tilde{\varphi }}}_4\end{array}\right)=\left(\begin{array}{c}\kappa {\tilde{\theta }}_4\\ \kappa {\tilde{\varphi }}_4\end{array}\right),$$ 4.11

which leads to two negative eigenvalues for the linear stability, κ/k_F < 0. This, in turn, indicates that the instability can occur only if accompanied by the rigid-body motion of the cell. Here we note that the angle variables, ${\tilde{\theta }}_4$ and ${\tilde{\varphi }}_4$, do not generate any forces and torque. Inspecting the definition of ${\tilde{\theta }}_4$, we see that the force from the angles θ₁ − θ₂ is cancelled by that generated by θ₃ − θ₄ and the torque from the part θ₁ + θ₃ cancels that from θ₂ + θ₄.

(c). General N case

The two simple examples above enable us to now characterize the instabilities in the general N case. Specifically, we expect that the instabilities are associated with the rigid-body translation and rotation of the cell body even when N≥5. We introduce the new angle variables as found in the expressions of F_prop (2.27) and M_prop (2.28)

$${\tilde{\theta }}_1=\sum _{i=1}^N{\theta }_i\sin {\mathit{\Theta }}_i,{\tilde{\theta }}_2=\sum _{i=1}^N{\theta }_i\cos {\mathit{\Theta }}_i,{\tilde{\theta }}_3=\sum _{i=1}^N{\theta }_i$$ 4.12

and

$${\tilde{\varphi }}_1=\sum _{i=1}^N{\varphi }_i\sin {\mathit{\Theta }}_i,{\tilde{\varphi }}_2=\sum _{i=1}^N{\varphi }_i\cos {\mathit{\Theta }}_i,{\tilde{\varphi }}_3=\sum _{i=1}^N{\varphi }_i.$$ 4.13

We first consider the mode associated with the translation and rotation along the x-axis. The resulting 2 × 2 matrices are

$$\left(\begin{array}{cc}{C}_{D1}& -k_T\\ -\frac{N}{2}{k}_T& k_F\end{array}\right)\left(\begin{array}{c}{U}_x\\ {\dot{\tilde{\theta }}}_1\end{array}\right)=\left(\begin{array}{c}{\omega }_0{K}_T{\tilde{\theta }}_1\\ \kappa {\tilde{\theta }}_1\end{array}\right)$$ 4.14

and

$$\left(\begin{array}{cc}{C}_{R1}& (k_T+k_F)\\ \frac{N}{2}(k_T+k_F)& k_F\end{array}\right)\left(\begin{array}{c}{\mathit{\Omega }}_x\\ {\dot{\tilde{\varphi }}}_1\end{array}\right)=\left(\begin{array}{c}{\omega }_0(K_F{\tilde{\theta }}_1-K_T{\tilde{\varphi }}_1)\\ \kappa {\tilde{\varphi }}_1\end{array}\right),$$ 4.15

from which we obtain two eigenvalues

$$A_T={\mathrm{\Delta }}_T^{-1}(\frac{N}{2}|K_T{k}_T|{\omega }_0-|C_{D1}|\kappa )$$ 4.16

and

$$A_{R3}={\mathrm{\Delta }}_{R3}^{-1}(\frac{N}{2}|K_T(k_T+k_F)|{\omega }_0-|C_{R1}|\kappa ),$$ 4.17

where we have introduced the determinants Δ_T = C_D1k_F − (N/2)k²_T and Δ_R3 = C_R1k_F − (N/2)(k_T + k_F)² which are positive due to the negative-definiteness of the resistance matrices. Expressions (4.16) and (4.17) are similar to the results obtained for N = 3 and N = 4, respectively.

As expected by symmetry, the modes associated with the translation and rotation along y are similar and the eigenvalues are the same as in the x-direction, i.e. A_T and A_R3.

We then proceed to investigating the modes along the z-axis and obtain the 2 × 2 matrices

$$\left(\begin{array}{cc}{C}_{D3}& -k_T\\ -N{k}_T& k_F\end{array}\right)\left(\begin{array}{c}{U}_z\\ {\dot{\tilde{\varphi }}}_3\end{array}\right)=\left(\begin{array}{c}{\omega }_0{K}_T{\tilde{\varphi }}_3\\ \kappa {\tilde{\varphi }}_3\end{array}\right)$$ 4.18

and

$$\left(\begin{array}{cc}{C}_{R3}& (k_T+k_F)\\ N(k_T+k_F)& k_F\end{array}\right)\left(\begin{array}{c}{\mathit{\Omega }}_z\\ {\dot{\tilde{\theta }}}_3\end{array}\right)=\left(\begin{array}{c}{\omega }_0(K_F{\tilde{\varphi }}_3-K_T{\tilde{\theta }}_3)\\ \kappa {\tilde{\theta }}_3\end{array}\right).$$ 4.19

This system has eigenvalues

$$A_{T3}={\mathrm{\Delta }}_{T3}^{-1}(N|K_T{k}_T|{\omega }_0-|C_{D3}|\kappa )$$ 4.20

and

$$A_R={\mathrm{\Delta }}_R^{-1}(N|K_T(k_T+k_F)|{\omega }_0-|C_{R3}|\kappa ),$$ 4.21

with determinants Δ_T = C_D1k_F − Nk²_T and Δ_R3 = C_R1k_F − N(k_T + k_F)² The eigenvalues, (4.20) and (4.21), again reproduce the results of N = 3 and N = 4.

The eigenvectors obtained so far are associated with three pure rotational modes and three combined translation/rotation modes along the same axis. The remaining degrees of freedom associated with the other 2N − 6 angular variables do not affect the stability of the cell, which can be summarized to the following statement.

Theorem 4.1. —

The linear system (2.12) includes the six modes associated with a rigid-body motion, with eigenvalues A_T, A_T, A_T3, A_R, A_R3, A_R3. The remaining 2N − 6 degrees of freedom all generate identical negative eigenvalues, κ/k_F < 0.

In order to complete the proof of the above statement, we need to rearrange the angle variables so as to diagonalize the remaining 2N − 6 degrees of freedom. We first prepare linearly independent N in-plane angle variables, ${\tilde{\theta }}_i$, for i = 1, …, N, in which the angle variables ${\tilde{\theta }}_1,{\tilde{\theta }}_2,{\tilde{\theta }}_3$ defined in (4.12) are included. When N≥4, the diagonalization can then be achieved if we pick the remaining angle variables so that they do not generate any effective force and torque. This is possible for an arbitrary ${\tilde{\theta }}_i$ for i≥4, since we can add ${\tilde{\theta }}_1,{\tilde{\theta }}_2,{\tilde{\theta }}_3$ without disobeying the linear independence property for the set of angle variables. This argument can also be applied to the out-of-plane variables and the remaining 2N − 6 eigenvalues are found to be all identical and negative, κ/k_F < 0.

(d). Most unstable mode

We obtain 2N eigenvalues for the linear system, six of which can be positive. In this section, we examine the nature of the most unstable mode, which is the one expected to be relevant in an experiment. From equations (4.16), (4.17), (4.20) and (4.21), we obtain critical angular velocities, above which the system becomes linearly unstable, as

$${\omega }_{0T}=\frac{2|C_{D1}|}{N|K_T{k}_T|}\kappa ,{\omega }_{0T3}=\frac{|C_{D3}|}{N|K_T{k}_T|}\kappa$$ 4.22

and

$${\omega }_{0R}=\frac{|C_{R3}|}{N|K_T(k_T+k_F)|}\kappa ,{\omega }_{0R3}=\frac{2|C_{R1}|}{N|K_T(k_T+k_F)|}\kappa .$$ 4.23

These values are all positive, indicating that the system is stable in the case where the flagellar filaments pull on the cell body and that the instability can occur only when flagella push. From equations (4.1) and (4.2), we readily obtain the comparison between the critical values for the in-plane and out-of-plane instabilities as

$${\omega }_{0T3}<{\omega }_{0T}\mathrm{and}{\omega }_{0R}<{\omega }_{0R3},$$ 4.24

respectively, which indicate that the most unstable mode is either the translation towards the z-axis (with combined rotation around the same direction) or pure rotation around the z-axis.

Notably, the expressions of the critical values include those of the N = 2 case, (3.9) and (3.10). However, due to the symmetry of the system, the eigenvalues are degenerated and the relation (4.24) becomes equalities, ω_0T3 = ω_0T and ω_0R = ω_0R3. Nonetheless, the expressions of ω_0T3 and ω_0R in (4.22) and (4.23) can be obtained when we substitute the constants k_C↦(N/2)k_C, k_T↦(N/2)k_T and k_F↦(N/2)k_F in (3.9) and (3.10). Thus, the rod-like flagellar model examined for N = 2 can also be applied in the general N case, and replacing c↦(N/2)c we obtain the same plots for the ratio of the two critical values, r, as in figure 4a. This indicates that the increase in the value of N can remove the possibility of r > 1, and therefore the translation instability would always be the most unstable mode for pushing flagella.

We note that simulation results with N = 4, which corresponds to a typical number of flagella for E. coli [8], showed translation in one direction along with rotation around the same axis [26], a result consistent with our stability analysis. We also note that the critical values (4.22) and (4.23) do not depend on the value of the torque generated by the flagellar rotation, K_F, but they only depend on the force generated by each rotating flagellum. By contrast, the value of K_F appears in the eigenvector of the translation mode and cells with large K_F undergo rapid rotation.

5. Small chirality effects

The analysis in the previous sections neglected the diagonal components of the matrix K⁽⁰⁾_TF. In this section, we reincorporate the diagonal terms k_D and solve the resulting linear stability problem. Since the diagonal components are small compared to the off-diagonal terms, we may treat the full problem as a perturbation from the results obtained in the previous sections.

As in the previous sections, the linear stability problem is written $\mathcal{A}\mathbf{\Phi }=\mathit{b}$ where straightforward calculations now lead the matrix (see also appendix A)

$$\mathcal{A}=\left(\begin{array}{cccccccc}{C}_{D1}& 0& 0& C_{C1}& 0& 0& {\mathit{C}}_{TF1}^{\mathrm{T}}& {\mathit{D}}_{TF1}^{\mathrm{T}}\\ 0& C_{D2}& 0& 0& C_{C2}& 0& {\mathit{C}}_{TF2}^{\mathrm{T}}& {\mathit{D}}_{TF2}^{\mathrm{T}}\\ 0& 0& C_{D3}& 0& 0& C_{C3}& {\mathit{D}}_{TF3}^{\mathrm{T}}& {\mathit{C}}_{TF3}^{\mathrm{T}}\\ C_{C1}& 0& 0& C_{R1}& 0& 0& {\mathit{D}}_{TR1}^{\mathrm{T}}& {\mathit{C}}_{TR1}^{\mathrm{T}}\\ 0& C_{C2}& 0& 0& C_{R2}& 0& {\mathit{D}}_{TR2}^{\mathrm{T}}& {\mathit{C}}_{TR2}^{\mathrm{T}}\\ 0& 0& C_{C3}& 0& 0& C_{R3}& {\mathit{C}}_{TR3}^{\mathrm{T}}& {\mathit{D}}_{TR3}^{\mathrm{T}}\\ {\mathit{C}}_{TF1}& {\mathit{C}}_{TF2}& {\mathit{D}}_{TF3}& {\mathit{D}}_{TR1}& {\mathit{D}}_{TR2}& {\mathit{C}}_{TR3}& k_F{\mathbf{1}}_N& {\mathbf{0}}_N\\ {\mathit{D}}_{TF1}& {\mathit{D}}_{TF2}& {\mathit{C}}_{TF3}& {\mathit{C}}_{TR1}& {\mathit{C}}_{TR2}& {\mathit{D}}_{TR3}& {\mathbf{0}}_N& k_F{\mathbf{1}}_N\end{array}\right),$$ 5.1

with new components arising from the chirality given by

$$\begin{array}{rl}{C}_{C1}& =\sum _{i=1}^N(K_T{\cos }^2{\mathit{\Theta }}_i+k_D{\sin }^2{\mathit{\Theta }}_i),\end{array}$$ 5.2

$$\begin{array}{rl}{C}_{C2}& =\sum _{i=1}^N(K_T{\sin }^2{\mathit{\Theta }}_i+k_D{\cos }^2{\mathit{\Theta }}_i)\end{array}$$ 5.3

$$\begin{array}{rl}\mathrm{and}{C}_{C3}& =N{k}_D,\end{array}$$ 5.4

and new N-dimensional vectors

$$\begin{array}{rl}& {\mathit{D}}_{TF1}={\mathit{D}}_{RF1}={(k_D\sin {\mathit{\Theta }}_1,\dots ,k_D\sin {\mathit{\Theta }}_N)}^{\mathrm{T}},\end{array}$$ 5.5

$$\begin{array}{rl}& {\mathit{D}}_{TF2}={\mathit{D}}_{RF2}={(-k_D\cos {\mathit{\Theta }}_1,\dots ,-k_D\cos {\mathit{\Theta }}_N)}^{\mathrm{T}}\end{array}$$ 5.6

$$\begin{array}{r}\mathrm{and}{\mathit{D}}_{TF3}=-{\mathit{D}}_{RF3}={(k_D,\dots ,k_D)}^{\mathrm{T}}.\end{array}$$ 5.7

With the use of the new angle variables (4.12) and (4.13), we may again reduce the linear problem into 4 × 4 blocks associated with the jth (j = 1, 2, 3) component of the force and torque, while the remaining degrees of freedom yield only negative eigenvalues for the stability problem. The explicit form along the x-direction can be computed as

$$\left(\begin{array}{cccc}{C}_{D1}& C_{C1}& C_{TF1}& D_{TF1}\\ C_{C1}& C_{R1}& D_{TR1}& C_{TR1}\\ C_{TF1}& D_{TR1}& k_F& 0\\ D_{TF1}& C_{TR1}& 0& k_F\end{array}\right)\left(\begin{array}{c}{U}_1\\ {\mathit{\Omega }}_1\\ {\dot{\tilde{\theta }}}_1\\ {\dot{\tilde{\varphi }}}_1\end{array}\right)=\left(\begin{array}{c}{\omega }_0{K}_T{\tilde{\theta }}_1\\ {\omega }_0(K_F{\tilde{\theta }}_1-K_T{\tilde{\varphi }}_1)\\ \kappa {\tilde{\theta }}_1\\ \kappa {\tilde{\varphi }}_1\end{array}\right).$$ 5.8

Inverting the matrix on the left-hand side in the previous equation leads to the following linear ordinary differential equations

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}{\tilde{\theta }}_1\\ {\tilde{\varphi }}_1\end{array}\right)=\left(\begin{array}{cc}{\tilde{A}}_T& {\tilde{A}}_{R3T}\\ {\tilde{A}}_{TR3}& {\tilde{A}}_{R3}\end{array}\right)\left(\begin{array}{c}{\tilde{\theta }}_1\\ {\tilde{\varphi }}_1\end{array}\right),$$ 5.9

for which we can characterize the linear stability as in the previous sections. Using the small parameter δ to measure the relative magnitude of the chirality effects in the resistance matrix, δ∼k_D/k_F∼10⁻² for the typical parameters of E. coli bacteria, we may expand the matrix in equation (5.9) at first order in δ as Ã_T = A_T + δA′_T, Ã_R3T = δA′_R3T, Ã_TR3 = A_TR3 + δA′_TR3, Ã_R3 = A_R3 + δA′_R3. This results in similar eigenvalues and eigenvectors for the system with changes of magnitude of order δ. However, as a result of the coupling term Ã_R3T, the pure rotation modes no longer exist and all eigenmodes are now associated with translation in x-direction (note that since the changes due to chirality are small, former rotation modes are still dominated by rotation and generate small net locomotion).

The analysis along the y- and z-directions are similar and we obtain perturbed eigenvectors and eigenvectors from those obtained in the previous sections. Except for the six angle variables, all other modes continue to have stable eigenvalues κ/k_F( < 0) as shown in the previous section, which can be summarized into the following statement.

Theorem 5.1. —

The linear stability problem characterized by matrix (5.1) includes six modes associated with rigid-body motion, and the remaining 2N − 6 degrees of freedom all generate identical negative eigenvalues, κ/k_F < 0.

The elastohydrodynamic instability can occur if the flagellar filaments push the cell body, accompanied by the rigid motion of the whole cell, with critical angular velocities perturbed from those obtained in the previous section, ω_0T, ω_0T3, ω_0R, ω_0R3, since δ is small. All unstable modes now lead to translation in one direction accompanied by rotation along the same direction. However, there are two types of modes for each direction, translation-dominated and rotation-dominated modes, the latter of which becomes pure-rotation modes when chirality effects are neglected.

6. Discussion

In this paper, we investigated theoretically the elastohydrodynamic stability problem of a model bacterium with multiple flagellar filaments rotated with prescribed frequencies. We assumed that the cell was equipped with N identical flagella connected to a spherical body by a flexible elastic torque spring and that the flagella are initially arranged in a plane with equal angle intervals as to form a regular N-polygon. We first formulated the equations of motions of this system and showed that this configuration provides an equilibrium state where the cell body does not move.

We then proceeded to consider the linear stability problem in the case of negligible chirality in the flagellar filaments (active rods). When N = 2, two modes are obtained (translation and rotation) which can be unstable when the flagella push on the cell body provided the magnitude of this pushing force exceeds a critical value (or, for a fixed propulsion magnitude, provided the hook is sufficiently flexible). The translation mode is the more unstable for the typical parameters of real bacteria and corresponds to the translation in one direction with rotating around the same axis. However, when the flagellar lengths are of the same order as the cell radius, L∼R, the most unstable mode could be switched to the second mode where the cells rotate in place in the plane of the initial flagellar configuration with no associated translation.

We then extended our results to the general case of N flagellar filaments, and we found that there are always only six modes which can be unstable, all of which are associated with rigid-body motion of the cell. The most unstable mode induces translation towards the direction perpendicular to the plane in which the N flagella are initially arranged and is accompanied by rotation around the same axis. This analytical result is in agreement with numerical simulation with N = 4 helical flagella [26].

We finally reincorporated the chirality of the flagellar filaments which had been neglected in the previous sections. Chirality leads to small perturbations of the eigenvalues and eigenvectors for the linear stability, and there are still only six possible unstable modes for cells with pusher flagella associated with rigid motion of the whole cell. The rotation modes are now accompanied by a small translation of the cell due to chirality-induced coupling.

The theoretical results in this paper and the presence of rotation-dominated modes imply that multi-flagellated peritrichous bacteria with shorter flagella could fail to swim efficiently. By contrast, for cells with typical flagellar length L∼10, flagella produce a sufficient amount of propulsive thrust to lead to an instability to translation. A similar analysis could also be applied to synthetic particles propelled by bacterial flagella [32,33] and to the dynamics of an ovum pushed by multiple spermatozoa [29]. Note that the linear stability analysis performed in this paper can obviously not fully predict the nonlinear dynamics after the initial stages of the instability. Furthermore, as shown in appendix B, if one considers instead the case of flagella rotated by a constant torque applied in the direction normal to the cell surface, all the possible unstable modes are accompanied by cell translation and pure-rotation modes disappear. This is in contrast to the case where the constant torque is applied along the long axis of the flagellar filament, for which the stability analysis coincides with the fixed-rotation case (see appendix B). These results emphasize the complexity of the multi-flagellated swimming dynamics.

Using typical parameter values for E. coli (R = 1 mm, L = 10 mm, N = 4) and the value of the viscosity for water (μ = 10⁻³ Pa s), we can estimate the critical flagellar rotation rate provided by our theory. The strength of the torque spring for an E. coli hook has been estimated to be in the range κ ≈ 2.9 - - 8.7 × 10⁻²¹ Nm using measured values for the hook bending stiffness and length [21,26], and we use the value κ = 5 × 10⁻²¹ Nm for the following discussions. From the flagellar propulsion force used by Riley et al. [26], we have K_T ≈ 7.0 × 10⁻¹⁶ N s. The drag coefficients are estimated as in §3a with c′ ≈ 0.13 and can be used to obtain an estimation of the critical rotation frequencies for a E. coli cell with N = 4 flagellar filaments. The critical values for the translation modes are predicted to be ν_0T ≈ 0.36 Hz and ν_0T3 ≈ 0.29 Hz, which are small compared with those for the pure rotation mode, ν_0R ≈ 1.33 Hz and ν_0R3 ≈ 1.34 Hz. Since the flagellar filaments of real cells rotate much faster (ν ≈ 100 Hz), the elastohydroynamic instability obtained in this paper is likely to be relevant to the locomotion of bacteria.

The model in our paper could be readily extended to the case of a spheroidal cell body if the case where the flagella are all initially arranged in the equatorial plane of the spheroid, and one would simply need to change the values of the drag coefficient C_D. When the cell body takes the shape of a prolate spheroid such as of E. coli, C_D1/C_D3 > 2 still holds and we obtain the same relation as (4.24). Other straightforward extensions include the situation in which the cell body is located near a planar infinite wall, a situation relevant to a sperm–egg cluster that tends to rotate without translation [29]. The predominance of rotation could be rationalized in that case using lubrication theory [30], which shows that drag coefficients C_D1 and C_D3 diverge as the spherical cell body approaches the wall, while the value of the rotation drag coefficient C_R3 remains very close to that in the bulk. As a result, the rotation mode would become in that case more unstable than the translation mode. Further theoretical work would be required to extend to more general situations such as for example a non-spherical cell body, non-symmetric flagellar configurations or non-identical flagella, emphasizing the rich diversity of the N-flagella problem.

Appendix A. Derivations of matrices (2.31) and (5.1)

In this appendix, we provide detailed derivations of the matrices (2.31) and (5.1) for the motion of the bacterium with N flagella arranged in a regular polygonal manner.

The N identical in-plane flagella with orientations e⁽ⁱ⁾ = R(Θ_i;e_z) · e_x provide a stationary configuration. Considering small disturbances around the equilibrium, with angles |θ_i|, |ϕ_i|≪1, we directly compute the matrix entries noting that one only needs the leading-order contributions for the linear stability.

We first consider K⁽ⁱ⁾_C, which is computed from (2.25),

$${\mathsf{K}}_C^{(i)}={\mathsf{R}}_i\cdot {\mathsf{K}}_C^{(0)}\cdot {\mathsf{R}}_i^{-1}\simeq \left(\begin{array}{ccc}{K}_C{\cos }^2{\mathit{\Theta }}_i+k_C{\sin }^2{\mathit{\Theta }}_i& (K_C-k_C)\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i& 0\\ (K_C-k_C)\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i& K_C{\sin }^2{\mathit{\Theta }}_i+k_C{\cos }^2{\mathit{\Theta }}_i& 0\\ 0& 0& k_C\end{array}\right),$$ A 1

where the symbol ≃ is used here to mean the leading-order contribution. The expression for K_TT is given by summation of this matrix over the indices i.

For the off-diagonal part, we need $\sum _{i=1}^N({\mathsf{K}}_C^{(i)}\cdot {\mathsf{A}}_i^{\prime }+{\mathsf{K}}_{TF}^{(i)})$. From expression (A 1), we have

$${\mathsf{K}}_C^{(i)}\cdot {\mathsf{A}}_i^{\prime }\simeq \left(\begin{array}{ccc}0& 0& -k_C\sin {\mathit{\Theta }}_i\\ 0& 0& k_C\cos {\mathit{\Theta }}_i\\ k_C\sin {\mathit{\Theta }}_i& -k_C\cos {\mathit{\Theta }}_i& 0\end{array}\right),$$ A 2

and using (2.25) we obtain

$${\mathsf{K}}_{TF}^{(i)}\simeq \left(\begin{array}{ccc}{K}_T{\cos }^2{\mathit{\Theta }}_i+k_D{\sin }^2{\mathit{\Theta }}_i& (K_T-k_D)\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i& -k_T\sin {\mathit{\Theta }}_i\\ (K_T-k_D)\cos {\mathit{\Theta }}_i\sin {\mathit{\Theta }}_i& K_T{\sin }^2{\mathit{\Theta }}_i+k_D{\cos }^2{\mathit{\Theta }}_i& k_T\cos {\mathit{\Theta }}_i\\ k_T\sin {\mathit{\Theta }}_i& -k_T\cos {\mathit{\Theta }}_i& k_D\end{array}\right).$$ A 3

The summations in (A 2) and (A 3) give the expression for K_TR and its transpose just follows for K_RT. The contributions of the K_T terms can be neglected following the approximation showing that k_D is negligible. For a helical filament, K_F scales as K_F∼C_Nb²L, and comparing it with the leading-order term we have the relative magnitude as K_F/k_F∼(b/L)²∼10⁻³ using typical numbers for E. coli cells. Thus in the matrix (2.31), the K_F term can be neglected if we neglect k_D.

For the expression of K_RR, we need to calculate

$${\mathsf{K}}_{RR}=C_R\mathsf{1}+\sum _{i=1}^N({\mathsf{A}}_i^{\mathrm{\prime }\mathrm{T}}\cdot {\mathsf{K}}_C^{(i)}\cdot {\mathsf{A}}_i^{\prime }+{\mathsf{A}}_i^{\mathrm{\prime }\mathrm{T}}\cdot {\mathsf{K}}_{TF}^{(i)}+{\mathsf{K}}_{FT}^{(i)}\cdot {\mathsf{A}}_i^{\prime }+{\mathsf{K}}_{FF}^{(i)}),$$ A 4

which is obtained by straightforward calculations as

$$\begin{array}{rl}{\mathsf{A}}_i^{\mathrm{\prime }\mathrm{T}}\cdot {\mathsf{K}}_C^{(i)}\cdot {\mathsf{A}}_i^{(i)}& \simeq \left(\begin{array}{ccc}{k}_C{\sin }^2{\mathit{\Theta }}_i& -k_C\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i& 0\\ -k_C\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i& k_C{\cos }^2{\mathit{\Theta }}_i& 0\\ 0& 0& k_C\end{array}\right),\end{array}$$ A 5

$$\begin{array}{rl}{\mathsf{A}}_i^{\mathrm{\prime }\mathrm{T}}\cdot {\mathsf{K}}_{TF}^{(i)}& \simeq \left(\begin{array}{ccc}{k}_T{\sin }^2{\mathit{\Theta }}_i& -k_T\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i& k_D\sin {\mathit{\Theta }}_i\\ -k_T\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i& k_T{\cos }^2{\mathit{\Theta }}_i& -k_D\sin {\mathit{\Theta }}_i\\ -k_D\sin {\mathit{\Theta }}_i& k_D\sin {\mathit{\Theta }}_i& k_T\end{array}\right)\end{array}$$ A 6

$$\begin{array}{rl}\mathrm{and}{\mathsf{K}}_{FF}^{(i)}& \simeq \left(\begin{array}{ccc}{K}_F{\cos }^2{\mathit{\Theta }}_i+k_F{\sin }^2{\mathit{\Theta }}_i& (K_F-k_F)\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i& 0\\ (K_F-k_F)\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i& K_F{\sin }^2{\mathit{\Theta }}_i+k_F{\cos }^2{\mathit{\Theta }}_i& 0\\ 0& 0& k_F\end{array}\right).\end{array}$$ A 7

Using the equalities,

$$\sum _{i=1}^N\sin {\mathit{\Theta }}_i=\sum _{i=1}^N\cos {\mathit{\Theta }}_i=\sum _{i=1}^N\sin {\mathit{\Theta }}_i\cos {\mathit{\Theta }}_i=0,$$ A 9

and summing over the index i completes the computations for the matrix entries.

Appendix B. Torque-driven motility of N = 2 flagella

In this appendix, we briefly consider the bacterial model with N = 2 flagella in case where the torque, instead of the rotation, is prescribed for each flagellar filament. This will allow us to highlight the difference of the dynamics from the rotation-given problem. As in the main text, we assume identical flagella and axisymmetric propulsion. Using the same matrix form as (2.14), the torque-driven motility dynamics can be expressed as

$$\left(\begin{array}{ccc}{\mathsf{K}}_{TT}& {\mathsf{K}}_{TR}& {\mathsf{K}}_{TF}^{(i)}\\ {\mathsf{K}}_{RT}& {\mathsf{K}}_{RR}& {\mathsf{K}}_{RF}^{(i)}\\ {\mathsf{K}}_{FT}^{(i)}& {\mathsf{K}}_{RT}^{(i)}& {\mathsf{K}}_{FF}^{(i)}\end{array}\right)\left(\begin{array}{c}\mathit{U}\\ \mathit{\Omega }\\ {\mathit{\omega }}^{(i)}\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\\ -{\mathit{M}}_{\mathrm{elast}}^{(i)}-{\mathit{M}}_{\mathrm{motor}}^{(i)}\end{array}\right).$$ B 1

We use the decomposition of the flagellar rotation velocity vector, ω⁽ⁱ⁾ = ω⁽ⁱ⁾_t + ω⁽ⁱ⁾_n, and the commutative relations (2.19), to obtain the same form of the force and torque balance equations as (2.20), namely

$$\left(\begin{array}{ccc}{\mathsf{K}}_{TT}& {\mathsf{K}}_{TR}& {\mathsf{K}}_{TF}^{(i)}\\ {\mathsf{K}}_{RT}& {\mathsf{K}}_{RR}& {\mathsf{K}}_{RF}^{(i)}\end{array}\right)\left(\begin{array}{c}\mathit{U}\\ \mathit{\Omega }\\ {\mathit{\omega }}_n^{(i)}\end{array}\right)=\left(\begin{array}{c}-\sum _{i=1}^N{\mathsf{K}}_{TF}^{(i)}\cdot {\mathit{\omega }}_t^{(i)}\\ -\sum _{i=1}^N{\mathsf{K}}_{RF}^{(i)}\cdot {\mathit{\omega }}_t^{(i)}\end{array}\right).$$ B 2

The torque balance equation for each flagellum is

$${\mathsf{K}}_{FT}^{(i)}\cdot \mathit{U}+{\mathsf{K}}_{FR}^{(i)}\cdot \mathit{\Omega }+{\mathsf{K}}_{FF}^{(i)}\cdot ({\mathit{\omega }}_t^{(i)}+{\mathit{\omega }}_n^{(i)})=-{\mathit{M}}_{\mathrm{elast}}^{(i)}-{\mathit{M}}_{\mathrm{motor}}^{(i)},$$ B 3

which can be rewritten, using the variables in the flagellum-fixed frame, as

$${\mathsf{K}}_{FT}^{(0)}\cdot {\mathsf{R}}_i^{-1}\cdot \mathit{U}+{\mathsf{R}}_i^{-1}\cdot {\mathsf{K}}_{FR}^{(i)}\cdot \mathit{\Omega }+{\mathsf{K}}_{FF}^{(0)}\cdot ({\tilde{\mathit{\omega }}}_t^{(i)}+{\tilde{\mathit{\omega }}}_n^{(i)})=-{\tilde{\mathit{M}}}_{\mathrm{elast}}^{(i)}-{\tilde{\mathit{M}}}_{\mathrm{motor}}^{(i)}.$$ B 4

We next introduce the projection on to z-axis as Q₀ = 1 − P₀, and apply P₀ and Q₀ from the left side of equation (B 4). From the projection onto the x–y-plane, we obtain a similar torque balance equation as in the bottom row of the equation (2.20), namely

$${\mathsf{P}}_0\cdot {\mathsf{K}}_{FT}^{(0)}\cdot {\mathsf{R}}_i^{-1}\cdot \mathit{U}+{\mathsf{P}}_0\cdot {\mathsf{R}}_i^{-1}\cdot {\mathsf{K}}_{FR}^{(i)}\cdot \mathit{\Omega }+{\mathsf{K}}_{FF}^{(0)}\cdot {\tilde{\mathit{\omega }}}_n^{(i)}=-{\tilde{\mathit{M}}}_{\mathrm{elast}}^{(i)}-{\mathsf{P}}_0\cdot {\tilde{\mathit{M}}}_{\mathrm{motor}}^{(i)},$$ B 5

noting that the last term of the right-hand side is the only correction from the rotation-given problem.

The projection using Q₀ provides the equations for the tangential flagellar rotation velocity

$${\mathsf{Q}}_0\cdot {\mathsf{K}}_{FT}^{(0)}\cdot {\mathsf{R}}_i^{-1}\cdot \mathit{U}+{\mathsf{Q}}_0\cdot {\mathsf{R}}_i^{-1}\cdot {\mathsf{K}}_{FR}^{(i)}\cdot \mathit{\Omega }+{\mathsf{K}}_{FF}^{(0)}\cdot {\tilde{\mathit{\omega }}}_t^{(i)}=-{\mathsf{Q}}_0\cdot {\tilde{\mathit{M}}}_{\mathrm{motor}}^{(i)},$$ B 6

and we proceed to calculate the detailed expressions for the linear stability analysis around the equilibrium configuration with N = 2.

We need to assume the exact form of the function ${\tilde{\mathit{M}}}_{\mathrm{motor}}^{(i)}$, and here we consider two different possibles for the constant torque: (i) constant torque applied along the flagellar orientation (M⁽ⁱ⁾_motor = M₀e⁽ⁱ⁾) and (ii) constant torque applied along the normal to the cell surface (M⁽ⁱ⁾_motor = M₀n⁽ⁱ⁾).

When |θ_i|, |ϕ_i|≪1, the leading-order value of the right-hand side of (B 6) is given by −M₀e_z in both torque models. The third term on the left-hand side of (B 6) is simply ${\mathsf{K}}_{FF}^{(0)}\cdot {\tilde{\mathit{\omega }}}_t^{(i)}=K_F{\omega }_0{\mathit{e}}_z$, and thus we can neglect O(|θ_i|, |ϕ_i|) contribution in the first two terms of (B 6) in order to determine the leading-order term of ω₀. With calculations similar to those in appendix A, we obtain the O(1) contribution from the first term as Q₀ · K⁽⁰⁾_FT · R⁻¹_i · U≃K_F(cosΘ_iU_x + sinΘ_iU_y)e_z, which is however zero as a consequence of the fact that U_x = sinΘ_i = 0 for the linear stability problem with N = 2. The second term is calculated as Q₀ · R⁻¹_i · K⁽ⁱ⁾_FR · Ω≃K_F(Ω_xcosΘ_i + Ω_ysinΘ_i)e_z and this is again found to be zero since Ω_x and sinΘ_i are zero for the linear stability problem with N = 2.

In summary, we obtain the expression for the flagellar rotation rate, ω₀,

$${\omega }_0=\frac{M_0}{|K_F|},$$ B 7

and ω₀ becomes positive when M₀ > 0. Equations (B 2) and (B 5) provide therefore a set of equations similar to (2.20) for the rotation-given problem. We note the presence of the additional term ${\mathsf{P}}_0\cdot {\tilde{\mathit{M}}}_{\mathrm{motor}}^{(i)}$ in equation (B 5). This correction term, however, vanishes for the torque model (i), and thus this torque-driven motility problem coincidences with the rotation-given motility when N = 2.

We then consider the torque model (ii) where the constant torque is applied along the normal to the cell surface. In that case, the correction term contributes an external bending torque, since ${\mathsf{P}}_0\cdot {\tilde{\mathit{M}}}_{\mathrm{motor}}^{(i)}\simeq M_0({\theta }_i{\mathit{e}}_y-{\varphi }_i{\mathit{e}}_x)$. Proceeding with the linear stability analysis, as in equations (3.1)–(3.4), we obtain four blocks of 2 × 2 matrices, using the angle variables θ₊ = θ₁ + θ₂, θ₋ = θ₁ − θ₂, ϕ₊ = ϕ₁ + ϕ₂ and ϕ₋ = ϕ₁ − ϕ₂,

$$\begin{array}{rl}& \left(\begin{array}{cc}{C}_D^{\prime }& k_T\\ 2k_T& k_F\end{array}\right)\left(\begin{array}{c}{U}_z\\ {\dot{\varphi }}_{+}\end{array}\right)=\left(\begin{array}{c}-{\omega }_0{K}_T{\varphi }_{+}\\ \kappa {\varphi }_{+}+M_0{\theta }_{+}\end{array}\right),\end{array}$$ B 8

$$\begin{array}{rl}& \left(\begin{array}{cc}{C}_R^{\prime }& k_T+k_F\\ 2(k_T+k_F)& k_F\end{array}\right)\left(\begin{array}{c}{\mathit{\Omega }}_z\\ {\dot{\theta }}_{+}\end{array}\right)=\left(\begin{array}{c}-{\omega }_0{K}_T{\varphi }_{+}-{\omega }_0{K}_F{\theta }_{+}\\ \kappa {\theta }_{+}-M_0{\varphi }_{+}\end{array}\right),\end{array}$$ B 9

$$\begin{array}{rl}& \left(\begin{array}{cc}{C}_D^{\prime }& k_T\\ 2k_T& k_F\end{array}\right)\left(\begin{array}{c}{U}_y\\ {\dot{\theta }}_{-}\end{array}\right)=\left(\begin{array}{c}-{\omega }_0{K}_T{\theta }_{-}\\ \kappa {\theta }_{-}-M_0{\varphi }_{-}\end{array}\right)\end{array}$$ B 10

$$\begin{array}{r}\mathrm{and}\left(\begin{array}{cc}{C}_R^{\prime }& -(k_T+k_F)\\ -2(k_T+k_F)& k_F\end{array}\right)\left(\begin{array}{c}{\mathit{\Omega }}_y\\ {\dot{\varphi }}_{-}\end{array}\right)=\left(\begin{array}{c}{\omega }_0{K}_T{\varphi }_{-}-{\omega }_0{K}_F{\theta }_{-}\\ \kappa {\varphi }_{-}+M_0{\theta }_{-}\end{array}\right).\end{array}$$ B 11

Solving equations (B 8) and (B 9) with respect to θ + and ϕ + , we obtain the linear ordinary differential equations

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(\begin{array}{c}{\theta }_{+}\\ {\varphi }_{+}\end{array}\right)=\left(\begin{array}{cc}{A}_R& A_{RT}\\ A_{TR}& A_T\end{array}\right)\left(\begin{array}{c}{\theta }_{+}\\ {\varphi }_{+}\end{array}\right).$$ B 12

The diagonal components are

$$A_T={\mathrm{\Delta }}_D^{-1}(2{\omega }_0|K_T{k}_T|-\kappa |C_D^{\prime }|)$$ B 13

and

$$A_R={\mathrm{\Delta }}_R^{-1}(2{\omega }_0|K_T(k_T+k_F)|-\kappa |C_R^{\prime }|)$$ B 14

are the same as in the rotation-given problem (3.6) and (3.7). By contrast, the off-diagonal components includes the corrections

$$A_{RT}={\mathrm{\Delta }}_R^{-1}(2{\omega }_0|K_T(k_T+k_F)|+M_0|C_D^{\prime }|)$$ B 15

and

$$A_{TR}={\mathrm{\Delta }}_D^{-1}(-M_0|C_D^{\prime }|),$$ B 16

and therefore the stability characteristics could be different from the rotation-given problem.

When M₀ < 0, the flagellar filaments pull on the cell-body into fluid and we find that the eigenvalues are all negative since A_T, A_RT, A_R < 0 and A_TR > 0. Hence the dynamics is always linearly stable. By contrast, when M₀ > 0, the eigenvalues are still both negative for small values of M₀, but become positive when M₀ becomes sufficiently large, and there are two critical values of M₀ above which instability can occur. Both unstable modes, however, combine translation with rotation and the pure rotation modes disappear (in contrast to the rotation-given motility problem). The critical flagellar rotation velocities ω*₀ in this case lie between the critical values of the rotation-given problem (3.9) and (3.10)

$$min\{{\omega }_{0T},{\omega }_{0R}\}\le {\omega }_0^{\ast }\le max\{{\omega }_{0T},{\omega }_{0R}\}.$$ B 17

Note that, by symmetry, the same eigenvalues follow for the linear ordinal differential equations obeyed by the variables θ − and ϕ_i derived from equations (B 10) and (B 11).

Data accessibility

This paper has no additional data.

Authors' contributions

K.I. and E.L. designed the research, developed the mathematical model and wrote the paper. K.I. analysed the model.

Competing interests

The authors declare that they have no competing interests.

Funding

This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 682754 to E.L.). K.I. is supported by MEXT Leading Initiative for Excellent Young Researchers (LEADER), JSPS KAKENHI (grand no. JP18K13456) and JSPS Overseas Research Fellowship (29-0146).