Mechanistic origin of cell-size control and homeostasis in bacteria

SUMMARY

Evolutionarily divergent bacteria share a common phenomenological strategy for cell-size homeostasis under steady-state conditions. In the presence of inherent physiological stochasticity, cells following this “adder” principle gradually return to their steady-state size by adding a constant volume between birth and division regardless of their size at birth. However, the mechanism of the adder has been unknown despite intense efforts. In this work, we show that the adder is a direct consequence of two general processes in biology: (1) threshold -- accumulation of initiators and precursors required for cell division to a respective fixed number, and (2) balanced biosynthesis -- maintenance of their production proportional to volume growth. This mechanism is naturally robust to static growth inhibition, but also allows us to “reprogram” cell-size homeostasis in a quantitatively predictive manner in both Gram-negative Escherichia coli and Gram-positive Bacillus subtilis. By generating dynamic oscillations in the concentration of the division protein FtsZ, we were able to oscillate cell size at division and systematically break the adder. In contrast, periodic induction of replication initiator protein DnaA caused oscillations in cell size at initiation, but did not alter division size or the adder. Finally, we were able to restore the adder phenotype in slow-growing E. coli, the only known steady-state growth condition wherein E. coli significantly deviates from the adder, by repressing active degradation of division proteins. Together these results show that cell division and replication initiation are independently controlled at the gene-expression level, and that division processes exclusively drive cell-size homeostasis in bacteria.

Graphical Abstract

Si and Le Treut et al. show that cell-size homeostasis in bacteria is exclusively driven by accumulation of division proteins to a threshold and their balanced biosynthesis during cell elongation. This mechanistic insight allowed them to reprogram cell-size homeostasis in both E. coli and B. subtilis. Evolutionary implications are discussed.

INTRODUCTION

Cellular physiology is composed of inherently stochastic processes [1]. Cell size at birth can fluctuate due to asymmetric division events or alterations in the timing or speed of constriction. Without homeostatic control, cell size in a continuous lineage would diverge with each division cycle. Evolutionarily divergent organisms ensure size homeostasis at the single-cell level by following a phenomenological principle known as the “adder” [2–14]. A central property of the adder is that newborn cells deviating from the average size at birth add a nearly fixed volume between birth and division, allowing them to exponentially converge to the population average in each division cycle (Figure 1). The adder sharply contrasts with a “sizer,” in which cells divide when they reach a fixed size. The adder principle has been extended to eukaryotes from yeast [9, 10, 13] to mammalian cells [11, 12] that have long been considered as sizers employing cell-cycle checkpoints.

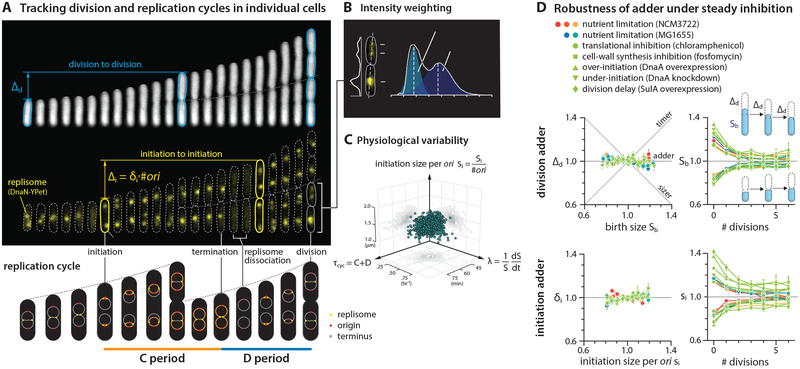
Figure 1: E. coli is both the initiation adder and division adder, robust to static inhibition of biosynthesis.

(A) Division adder vs. initiation adder. Upper: Δ_d is the added size between birth size S_b and division size S_d, and Δ_i is the total added size between two consecutive initiations. s_i is the cell size at initiation per origin, and δ_i is Δ_i per origin. Cell length is used as a proxy for cell size because cell width remains mostly constant during cell elongation [3] (Figure S4). Lower: Illustration of the replication cycle with two overlapping cell cycles.

(B) Resolving overlapping foci using intensity weighting (STAR Methods).

(C) Three major measured physiological parameters show 8%−20% of variation. Each dot represents measurement from a single cell.

(D) Under steady-state growth, E. coli is a division and an initiation adder, with or without static biosynthetic inhibition. Symbols are the binned data and error bars indicate standard errors of mean. In the correlation plots, the variables were rescaled by their means. 6 μM chloramphenicol and 0.05 μg/ml fosfomycin were used. See sample size in Table S3.

See also Figures S1 and S2, and Data S1.

The identification of the “adder” represented a major shift in our understanding of cell-size homeostasis [15, 16]. Naturally, many models have been proposed to explain the mechanistic origin of the adder phenotype. Most of these models can be classified into different groups by each model’s proposed implementation point of size control on the cell cycle. For example, recent works have suggested that the adder is governed by a replication-initiation-centric mechanism and division timing is determined by initiation in individual cells [17]. These models are based on the observation that cell size at initiation of DNA replication is invariant [18] at both single-cell [19] and population level [20]. These models are in contrast to a division-centric view of size homeostasis proposed earlier based on computer simulations [2] or biological constraints imposed on cellular resource allocation to division proteins [3, 21, 22]. Theoretical combination of replication and division controls has also been suggested at the phenomenological level [23, 24]. Alternatively, cell shape, or more specifically the surface-to-volume ratio of the cell, has also been suggested as the determining factor for size control [25].

In this work, we explain the mechanistic origin of cell-size homeostasis common to E. coli and B. subtilis, bacteria that diverged over a billion years ago. Specifically, we show that the adder phenotype is a direct consequence of two general processes in biology: (i) [threshold] accumulation of division initiators and precursors to a fixed threshold number per cell; and (ii) [balanced biosynthesis] their production is proportional to the growth of cell volume under steady-state condition. This mechanism allows us not only to “break” but also to “restore” the adder phenotype in a predictive manner under all major growth conditions.

Before proceeding to our results, we want to clarify the terminology. We use the term “cell-size control” for how cells determine their absolute size, and “cell-size homeostasis” for how cells correct deviations in size under steady-state growth. The two concepts are therefore closely related, yet differ with regard to whether emphasis is given to the requirement for threshold (for size control) or for balanced biosynthesis (for size homeostasis).

RESULTS AND DISCUSSION

Tracking replication and division cycles at the single-cell level

To illuminate the mechanisms underlying the adder principle, we performed a series of single-cell growth and cell-cycle tracking experiments under various growth conditions. We used a functional fluorescently-labeled replisome protein (DnaN-YPet) to image replication cycles, and a microfluidic mother machine to follow continuous lineages during steady-state growth [3, 26] (Figure 1A, Figure S1; STAR Methods; Data S1).

A major technical challenge arises in studying replication dynamics when two replisome foci spatially overlap, which makes it difficult to analyze overlapping replication cycles. To resolve this issue, we tracked multiple replication forks from initiation to termination by extending previous imaging methods [8, 19, 27, 28] using the “intensity weighting” techniques [29, 30] developed for super-resolution microscopy. This method allowed us to resolve overlapping replisome foci based on the number of peaks measured in the intensity distribution (Figure 1B; STAR Methods). These measurements showed 8%−20% of coefficients of variation (CV) for physiological parameters consistent with previous measurements, with the CV of cell size at initiation exhibiting one of the narrowest distributions (CV=8%) (Figures 1C and 2A; Methods S1–I).

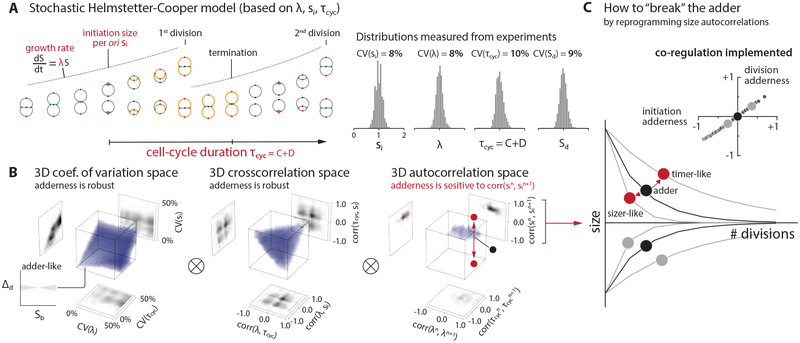
Figure 2: Survey of the 9-dimensional cell-size homeostasis space via stochastic Helmstetter-Cooper model assuming a co-regulation hypothesis between replication initiation and cell division.

(A) The schematics of single-cell simulation of cell growth and cell cycle progression. We used experimental data to introduce stochasticity to λ, τ_cyc, and s_i. (STAR Methods; Methods S1–I). We did not consider stochasticity in the septum position because its variability is the smallest (< 5%) among all measured parameters in E. coli [3].

(B) Survey results. Pearson coefficient was used to quantify both cross-correlations [e.g. corr(λ, τ_cyc)] and mother-daughter autocorrelations [e.g. corr(λⁿ, λⁿ⁺¹)]. Each 3-D plot is based on 1,000 simulations, and each simulation computed 10,000 division cycles (Methods S1–I). Purple color indicates an adder-like behavior defined as −0.1 < corr(Δ_d, S_b) < 0.1 (inset on bottom left). ^⊗ means the actual simulation took the convolution of all nine dimensions.

(C) Simulations revealed that the adder phenotype would break if the initiation size autocorrelation can be modulated, and the division adder and the initiation adder should co-vary (inset). The division adderness is corr(Δ_d, S_b), and the initiation adderness is corr(δ_i, s_i).

See also Figure S2, Data S1 and Methods S1.

E. coli follows an ‘initiation adder’ and a ‘division adder’, both robust to static inhibition of biosynthesis

Observation of wild type cells growing at steady state indicated the presence of two types of adder in E. coli: one functioning at division (hereafter a “division adder”) and the other at replication initiation (an “initiation adder”) (Figure 1). Parallel to the “division adder” [2, 3], the “initiation adder” is characterized by the addition of a nearly constant size per origin between consecutive replication cycles. This ensures that deviations in cell size (per ori) at initiation exponentially converge to the population average in each replication cycle [8, 31] (Figure 1D).

We next wanted to clarify the contribution of initiation and division to their respective adders. We utilized either tunable CRISPR interference [20, 32] to inhibit expression of dnaA that encodes the major bacterial DNA replication initiation protein, or an inducible-repressive promoter to modulate expression of a division inhibitor protein SulA. As expected, delays in replication and division both increased the average cell size (Figure S2B). However, neither perturbation had a detectable effect on the initiation adder or division adder (Figure 1D).

We also tested whether perturbations to global biosynthesis affect cell-size homeostasis, as they cause E. coli to deviate from the “growth law” of cell size, namely the well-established exponential relationship between the average cell size and the nutrient-imposed growth rate [20, 33]. In addition, previous work proposed accumulation of a fixed amount of cell-wall precursors as the mechanism of division adder [25]. We thus used either chloramphenicol or fosfomycin to target ribosomes or synthesis of cell-wall precursors, respectively, with the expectation that cells treated with these antibiotics would no longer exhibit the adder phenotype. In both cases, however, we found that defects in these major biosynthetic pathways did not affect either type of adder (Figure 1D).

Together these data show that E. coli possess the capacity to buffer steady inhibitions of cell cycle progression or general biosynthesis to maintain robust size homeostasis.

Using stochastic simulations to identify experimental conditions whereby E. coli should deviate from the adder

The robustness of adder posed unforeseen challenges for our attempts to identify the biological processes underlying the adder phenotype. Although we considered other types of perturbations or genetic screens, we realized that the physiological space was unrealistically large for brute-force search via single-cell time-lapse experiments. To circumvent the experimental challenges, we resorted to single-cell stochastic simulations and surveyed the entire physiological landscape (Figure 2A).

A subtle but important problem in our initial stochastic simulations was how to decide the timing of cell division. This issue is related to an outstanding question in bacterial physiology: whether replication and division are independently controlled or co-regulated [34]. We implemented the Helmstetter-Cooper model [35, 36] that is often interpreted to mean that initiation triggers division after a fixed elapsed time τcyc = C + D (Figures 1A and 2A) [17, 37]. To take into account biological stochasticity (Figures 1C and 2A, Figure S2A), we allowed for fluctuations in the three physiological variables, three cross-correlations, and three mother/daughter correlations (STAR Methods; Methods S1–I). When we incorporated this implicit co-regulation hypothesis and stochasticity [17] in our simulations, we observed that the initiation adder leads to the division adder (Figures 2B and 2C).

A brute-force numerical investigation of the entire parameter space suggested conditions under which size homeostasis should deviate from the adder and, importantly, an experimental means to “break” the adder. Specifically, when we varied the mother-daughter autocorrelation of the initiation size per ori s_i away from 0.5, cell-size homeostasis significantly deviated from the division adder. Otherwise, most other perturbations to physiological parameters did not severely affect the adder at division, reinforcing the general robustness of adder observed in our inhibition experiments (Figure 1D). In fact, in the stochastic Helmstetter-Cooper model, the mother-daughter autocorrelation of s_i alone completely determines the initiation adderness (Figure 2C; Methods S1–I). Since autocorrelation 0.5 is equivalent to exponential convergence of size deviations, we realized that the adder would break if we can experimentally modulate the speed of convergence [38].

Dynamic perturbation of replication initiator synthesis to the synthesis of replication initiators breaks the initiation adder

To experimentally test our predictions from simulations, we sought to alter the autocorrelation of cell size at initiation to modify cell size homeostasis. We found the properties of the DNA replication protein DnaA made it ideal for our test. DnaA is a widely conserved essential protein required for initiation of DNA replication in bacteria. In bacteria in which it has been examined, replication initiation depends in part on accumulation of a sufficient number of DnaA molecules at the origin of replication [39–41]. Previous studies and our data showed that an underexpression of dnaA causes an initiation delay, whereas an overexpression of dnaA causes premature initiation (Figure S3A) [20, 42].

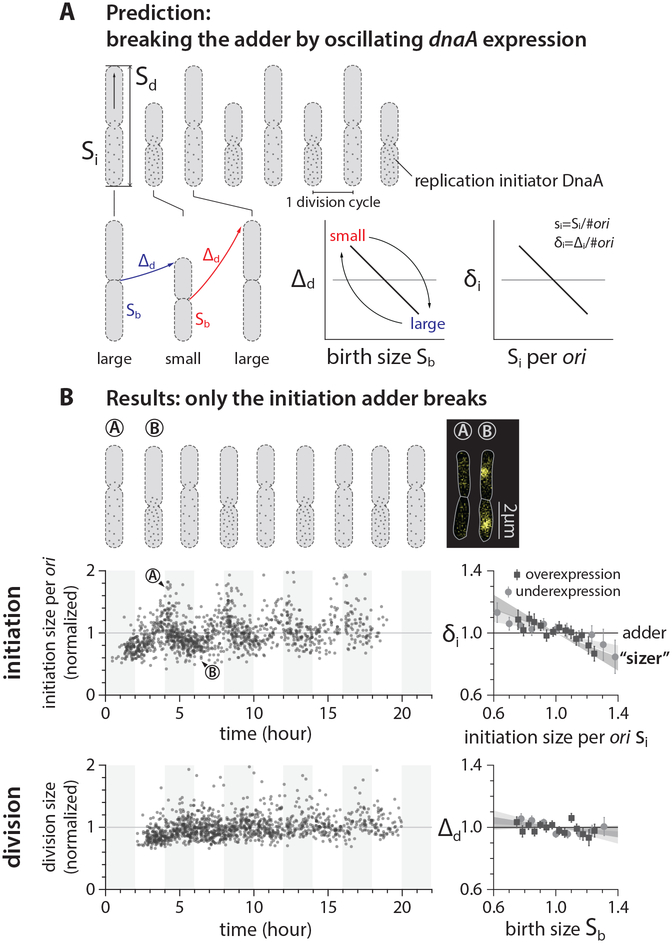
The relationship between dnaA expression level and initiation size led us to a relatively simple strategy to break the adder. If we periodically induce dnaA, the initiation size would oscillate at the same frequency as the induction. This should introduce negative autocorrelations to both initiation size and division size as illustrated in Figure 3A. The negative autocorrelations would be maximal when the period of oscillation T is two times the doubling time τ, because small-born cells add a larger size until division, whereas large-born cells add a smaller size until division, at every other division cycle (Figure 3A). Consequently, cell-size homeostasis during oscillations is sizer-like.

Figure 3: Dynamic perturbation of DnaA production breaks the initiation adder but not the division adder.

(A) Prediction of periodic induction of dnaA at every other generation (period T=2τ), based on the co-regulation hypothesis [17, 37]. Small-born cells would grow by larger added size, whereas large-born cells would grow by smaller added size, behaving like a sizer.

(B) Initiation size periodically oscillated, breaking the initiation adder. The division adder remained intact, refuting the co-regulation hypothesis. The period of IPTG infusion was about 4τ, and the IPTG concentration was altered between 200 μM and 0 μM (Methods S1–III.E). The left plots show the data of periodic underexpression of dnaA. Each dot corresponds to one division cycle of a single cell. In the correlation plots, the variables were normalized by their means and the shaded area represents the 95% confidence interval of linear fit to the respective raw scatter plot. The cell images overlay phase contrast with fluorescence of replisome markers.

See also Figure S3, STAR Methods, Methods S1 and Table S3.

In our actual experiments, we had to use T ≈ 4τ because of a significant induction and dilution time of dnaA (Figure S4A and Methods S1–III.E) [43]. Nevertheless, these experiments showed clear oscillations in the initiation size without noticeable changes in the growth rate (Figure 3B and Figure S3). The measured autocorrelations of initiation size decreased accordingly, decisively breaking the initiation adder as predicted by our simulations (Figure 3B).

The division adder is independent of initiation control, refuting the co-regulation hypothesis

To our surprise, and counter to the co-regulation hypothesis [17], the division adder remained intact even when the initiation adder no longer held by periodic induction of DnaA expression (Figure 3B). When initiation is delayed, the division size remains mostly constant as long as replication termination timing does not exceed the division timing. Thereafter, initiation delay causes an increase in division size (Figure S3D) [20]. Decoupling between the initiation adder and the division adder suggested that the timing of cell division, in fact, has its own independent control at the level of gene expression [2, 24, 44, 45]. We further reasoned that division timing is regulated by the dynamics of proteins and precursors required for division, rather than that of DnaA and other proteins required for replication initiation. We thus set out to break the division adder without breaking the initiation adder.

Dynamic perturbation to the synthesis of division initiators breaks the division adder but not the initiation adder

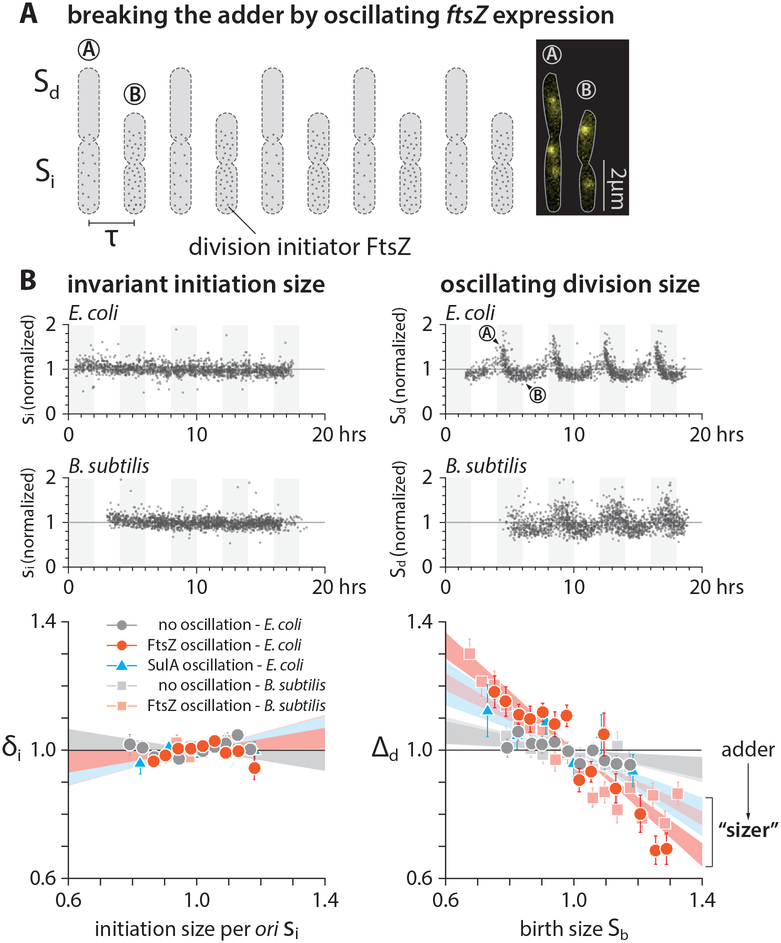
Cell division requires assembly of more than a dozen types of proteins and biomolecules at the future septum, including the enzymes required for synthesis of the septal cell wall. We elected to use the tubulin-like GTPase, FtsZ, because (like DnaA) it is highly conserved and assembles in an expression-level dependent manner. FtsZ-ring formation is required for assembly of all other components of the cell division machinery [46, 47], and the timing of division has been shown to be systematically delayed when FtsZ is underexpressed [48, 49]. FtsZ also has practical advantages since its genetic and cytological properties have been extensively characterized [50].

To determine if oscillations in FtsZ production break the division adder in the same manner that oscillations in DnaA break the initiation adder, we adopted a strain in which the wild-type ftsZ was expressed under the control of an inducible promoter (Figure 4A) [48, 51]. We also tracked replication dynamics using the fluorescent replisome marker. When we periodically underexpressed ftsZ with T ≈ 4τ, cell size at division oscillated with the same period, exclusively breaking the division adder without affecting initiation size (Figure 4B, Figures S4A and S4D). In addition, we obtained the same results by periodically producing the division inhibitor protein SulA (Figure 4C and Figure S4B).

Figure 4: Dynamic perturbation to division breaks the division adder but not the initiation adder.

(A) Dynamic modulation of division protein FtsZ oscillates the division size but not the initiation size.

(B) To periodically modulate the FtsZ production, IPTG concentration was alternated between 0 μM and 10 μM for E. coli, and xylose concentration between 0.1% w/v and 1% w/v for B. subtilis, at every 4τ. For periodic induction of sulA in E. coli, IPTG concentration was alternated between 0 μM and 40 μM, at every 4τ.

The data presentation of this figure is the same as that in Figure 3 (see caption). See also Figure S4 and Methods S1.

We repeated our experiments under different induction levels of ftsZ keeping the induction frequency same as before. The degree of deviations from the division adder systematically increased, yet the initiation adder remained intact, underscoring the independence between the initiation adder and the division adder in cell-size homeostasis (Figure 4B, Figures S4A and S4D; Methods S1–III). These results also show that cell division processes exclusively drive cell-size homeostasis in E. coli.

E. coli and B. subtilis likely share the same mechanistic origin of cell-size homeostasis

Next, we asked whether the exclusive role of cell division on size homeostasis, and its independence of initiation control, is a general feature of bacteria. To explore this idea, we repeated the FtsZ oscillation experiments in a model Gram-positive bacterium B. subtilis. B. subtilis is particularly interesting because, while DnaA and FtsZ are conserved in both bacteria, the mechanisms governing both replication initiation and division in B. subtilis differ in fundamental ways from those in E. coli [47, 52]. We constructed a strain that encodes ftsZ under an inducible P_xyl promoter as the sole source of FtsZ, in addition to the functional DnaN-mGFPmut2 fusion protein (Figure 4A) [53]. Together, these constructs permit periodic modulation of FtsZ levels and simultaneous tracking of replication dynamics.

Similar to E. coli, B. subtilis exhibited systematic deviations from the division adder when ftsZ expression was varied periodically. Furthermore, we found B. subtilis to be an initiation adder regardless of the oscillations (Figure 4B, Figures S4C and S4E). These results strongly suggested that E. coli and B. subtilis share the same mechanistic origin of cell-size homeostasis.

Mechanistic origin of cell-size homeostasis in bacteria: threshold and balanced biosynthesis

Our data so far indicated it is possible to break the adder phenotype using periodic oscillations in the production rate of cell-cycle proteins to perturb initiation size or division size (DnaA for the initiation adder and FtsZ for the division adder). This finding suggests that balanced biosynthesis of cell-cycle proteins is likely an important requirement for the adder phenotype.

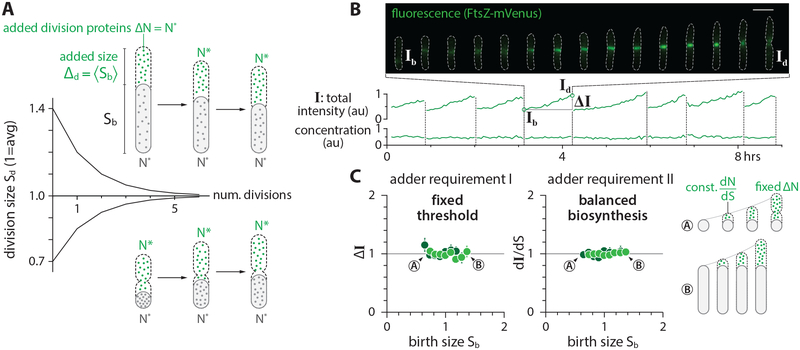
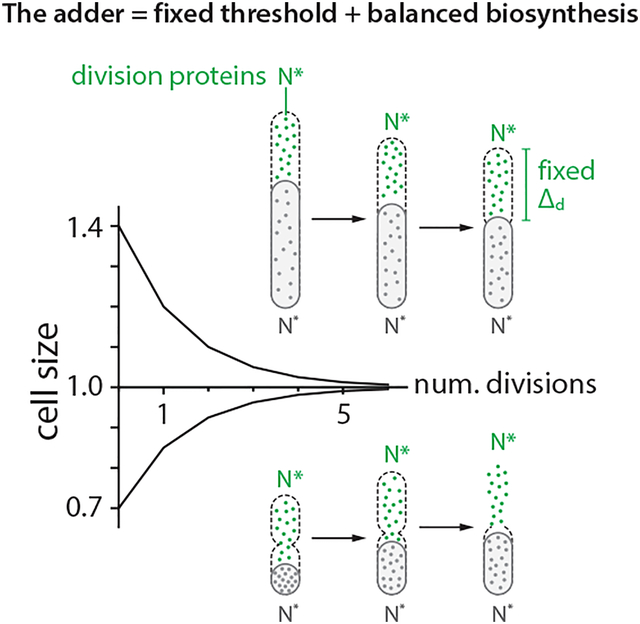
In balanced biosynthesis, the protein production rate is proportional to the rate cells increase their volume, irrespective of the protein concentration at birth. Cells therefore on average add a fixed number of proteins per unit volume during growth, and the total number of newly synthesized proteins is directly proportional to the total cell volume added since birth. Assuming balanced biosynthesis, a cell would be a division adder if division is triggered after accumulating a fixed number of division proteins, namely a fixed volume (Figure 5A; Methods S1–II). In other words, two experimentally testable assumptions are sufficient to explain the adder phenotype: (1) Threshold -- accumulation of initiators and precursors required for cell division to a fixed number, and (2) Balanced biosynthesis -- maintenance of their production proportional to volume growth.

Figure 5: The mechanistic origin of the adder and validation.

(A) The adder phenotype requires accumulation of division proteins to a fixed amount 2N* to trigger division, and their balanced biosynthesis during growth. Under these conditions, newborn cells are born either larger or smaller than the population average, but they on average contain N* division proteins. The two adder requirements ensure that both small-born and large-born cells add a constant size (namely, N* division proteins) in each generation.

(B) A typical timelapse sequence with FtsZ-mVenus. The total intensity was obtained by integrating the FtsZ-mVenus fluorescence intensity over the entire cell, which increases steadily from birth to division, tracking elongation of the cell. As a result, the FtsZ-mVenus concentration stays nearly constant within fluctuations.

(C) The synthesis and accumulation of FtsZ in E. coli cells fulfills both requirements for adder. The total added FtsZ number ΔN (estimated by the added fluorescence ΔI) and the synthesis per unit volume dN/dS were constant and independent of cell size at birth.

See also Figure S5 and Methods S1.

To test this idea, we measured the production rate and the accumulation of FtsZ in single cells. We adopted an E. coli strain expressing a nearly functional fusion ftsZ-mVenus as the sole endogenous copy of ftsZ [54]. We used the total fluorescence per cell, I, to estimate the total copy number of FtsZ per cell (Figure 5B; STAR Methods), and indeed found that I increased proportionally to the increase in cell volume in individual cells (Figure S5B). The production of FtsZ-mVenus per unit volume, dI/dt, during growth was independent of the cell size or FtsZ concentration at birth, consistent with the balanced biosynthesis hypothesis (Figure 5C; Figure S5C) [55, 56]. Furthermore, the total accumulation of FtsZ-mVenus between birth and division, ΔI = I_d - I_b, was also constant and independent of cell size or FtsZ concentration at birth I_b, supporting the threshold hypothesis (Figure 5C; Figure S5C) [21, 25, 57–59].

These results extend the previous observations that the Z-ring appears at mid-cell shortly after birth and FtsZ accumulates at the Z ring steadily over the course of the division cycle [60–63] (Figure 5B, Figure S5A). We also found that the onset of constriction coincides with when the total Z-ring intensity reaches its max value. The maximal Z-ring intensity was independent of the cell size or FtsZ concentration at birth (Figures S5A and S5C), reinforcing the molecular basis for the threshold model. As explained below, we further verified these hypotheses in our oscillation experiments.

Testing the mechanism of the adder in the FtsZ oscillation experiments

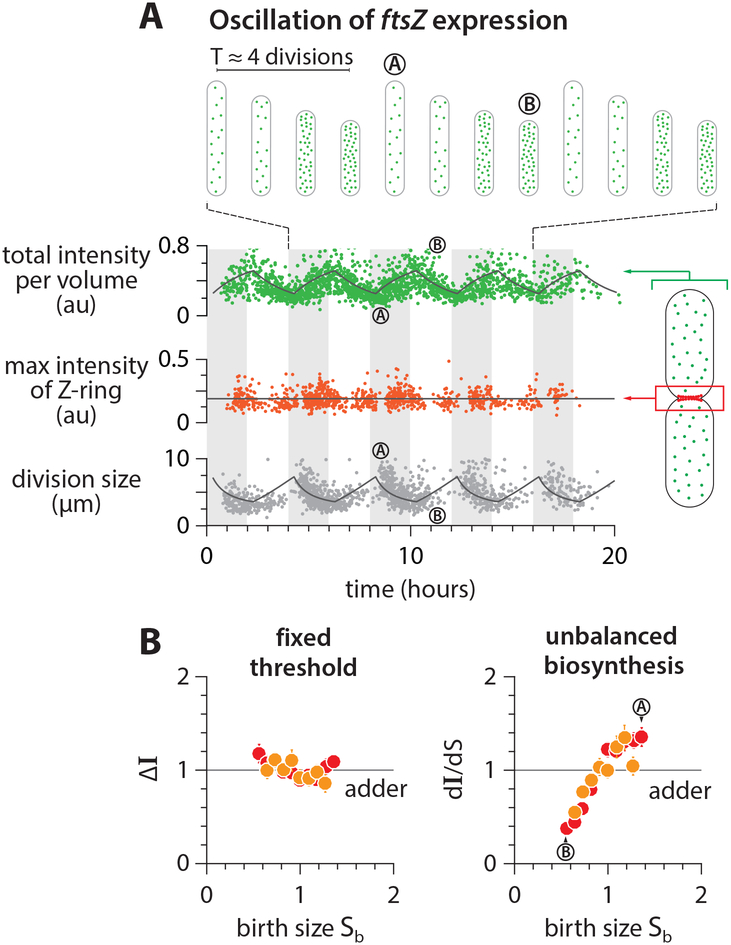
As the steady-state growth experiments supported the threshold and balanced biosynthesis hypotheses, we further tested them in new oscillation experiments. We combined the ftsZ-mVenus strain with the inducible system used in the oscillation experiments (Figure S6A; STAR Methods). As expected, FtsZ-mVenus concentration oscillated in response to the periodic induction, while the division size exhibited clear out-of-phase oscillations (Figure 6A; Methods S1–III). Despite the oscillations in FtsZ-mVenus concentration, the maximal Z-ring intensity at mid-cell and the total added fluorescence remained remarkably constant throughout the experiments regardless of the FtsZ concentration or cell size at birth (Figure 6A; Figure S6C).

Figure 6: Testing the mechanism of adder in the FtsZ oscillation experiments.

(A) Total FtsZ-mVenus concentration oscillates in response to the periodic induction, but the threshold amount at the septum is invariant. The amount of FtsZ accumulated in the septum ring was estimated by integrating the fluorescence intensity within a fixed area enclosing the mid-cell region (STAR Methods). The solid lines represent the prediction based on balanced biosynthesis and threshold model (Methods S1–III).

(B) The total added fluorescence ΔI and the max Z-ring intensity remain invariant with respect to birth size. By contrast, the production rate of FtsZ was variable due to oscillations.

Symbol colors indicate repeats of experiments, similar to Figure 5B. See also Figure S6.

The sizer-like behavior can also be explained by the out-of-phase oscillations in the FtsZ concentration and division size. During periodic induction of ftsZ, small-born daughter cells contain higher concentrations of FtsZ, because their mother cells accumulated FtsZ at a faster rate during high-level induction and therefore divided early. These new small-born daughter cells in turn experience low-level induction (Figure 6B, bottom), thus accumulate FtsZ to the fixed threshold number at a slower-rate and elongate longer to reach division (Figure 6B, top). Indeed, the added size Δ_d vs. newborn size s_b shows a characteristic sizer-like negative slope (Figure S6C; Figure 4).

How to restore the adder phenotype in slow-growing E. coli

While a wide range of evolutionarily divergent organisms are adders [15], a major exception has also been reported for E. coli. Specifically, Wallden et al. reported that size homeostasis, during slow growth in nutrient limitation, deviates from the adder [19]. We re-analyzed the published data in Wallden et al. and also performed our own experiments in the same growth condition. In contrast to Wallden et al., we found that the slope −0.31 in the Δ_d vs. newborn size S_b is in fact much closer to the adder (slope = 0) than the sizer (slope = −1) in both experiments. At the same time, the deviations from the adder is statistically significant (p-value = 1.4×10⁻⁶) as pointed out by Wallden et al.

Wallden et al. provided a possible explanation for their observation, based on the Helmstetter-Cooper model at the single-cell level. That is, the cell size at division can be written as S_d = s_i·exp(λτcyc) for non-overlapping cell cycles when cells grow in nutrient poor media. If s_i is invariant while τcyc is inversely proportional to λ at the single cell level because all biosynthesis equally limiting in slow growth conditions [19], λ_·τcyc = constant and therefore the invariant s_i implies S_d is fixed regardless of the birth size, thus the sizer. While elegant, this explanation is based on the co-regulation hypothesis and predicts both slope in Δ_d vs. s_b and Δ_i vs. s_i to be −1. For this prediction to be valid, both λ_·τcyc and s_i should be uncorrelated with birth size, which is in conflict with our data (Figure S7A). Indeed, our data obtained from the same growth condition as Wallden et al. instead shows that slow-growing E. coli is an initiation adder, and mildly deviates from the division adder (Figure 7; Figures S7B and S7C).

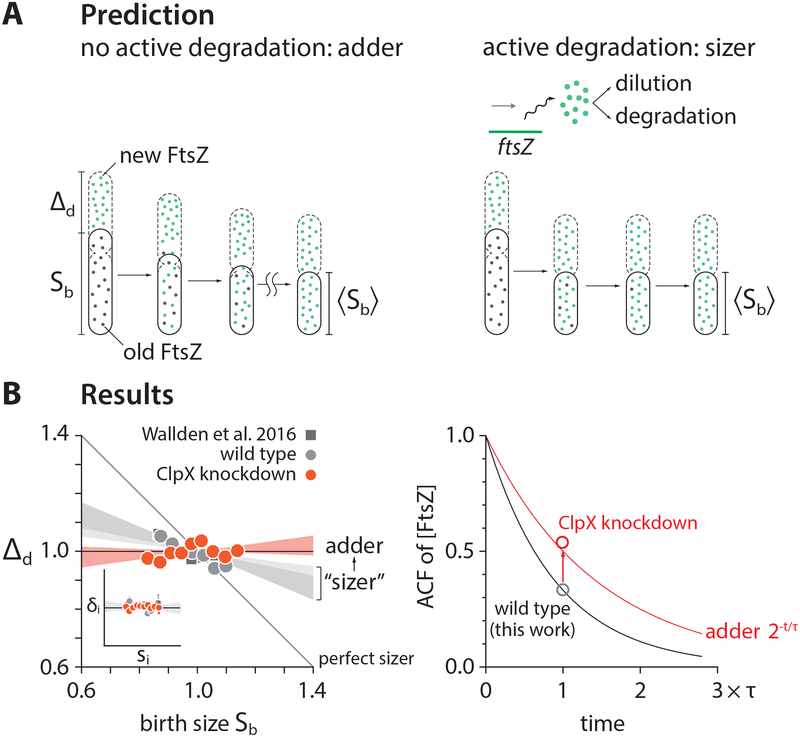
Figure 7: Restoring the division adder.

(A) Our hypothesis for why E. coli under slow growth conditions deviated from the adder towards the sizer reported in [19]. In slow-growing cells, significant amount of FtsZ is actively degraded by ClpXP [64, 65], which decreases autocorrelations of FtsZ concentration.

(B) We were able to restore the adder in slow growth conditions (doubling time ≈ 4 hours) by repressing clpX expression via tCRISPRi (STAR Methods), confirming our hypothesis. Inset shows that wildtype E. coli is an initiation adder in slow growth conditions. Each shaded area represents the 95% confidence interval of linear fit to the respective raw scatter plot.

See also Figure S7 and STAR Methods.

Our intuition for the discrepancy was that the slow-growing E. coli violates one or both requirements for the division adder (Figure 5). Specifically, we asked if FtsZ is actively degraded in slow growth conditions [64, 65], resulting in a higher turnover rate. Active degradation of FtsZ should decrease both autocorrelation of FtsZ concentration and division size (Figures 7A and 7B; STAR Methods). We further predicted that suppression of the activity of FtsZ would restore the division adder.

We tested our prediction by repressing clpX expression using our tCRISPRi system [32]. We found that clpX repression was indeed sufficient to fully restore the division adder (Figure 7B). The initiation adder was intact with or without the clpX repression (Figure S7C). These results provide strong experimental evidence for balanced biosynthesis and threshold as the requirements for cell-size homeostasis to be an adder.

Relationship with previous works

Balanced biosynthesis and threshold are general concepts in biology and have been implied in a number of papers since the 1970s from replication initiation [31] or cell division [3, 21, 59] in bacteria to mitotic control in eukaryotes [66]. The threshold model has also been explicitly put forward as the trigger of cell division as starved E. coli cells resume growth [64]. A recent work addressed whether cell shape contributes to size control [25], but we recognize its core implicit assumptions are balanced biosynthesis of cell-wall precursors and their accumulation to a threshold to build the septum.

Previous work independently showed that E. coli is a division adder but also questioned whether size control is implemented at initiation or division [2]. We have shown that division drives size homeostasis in E. coli and B. subtilis, but they are both initiation and division adders in steady state (Figure 1D). The independence between the two types of adders can only be revealed in non-steady-state growth (Figures 3 and 4). Subsequent analysis [67] has shown that the experimental evidence in Campos et al. may in fact agree with the initiation adder. As we show in Methods S1–IV, the initiation control model in [2] can result in unstable cell size regulation, but can be corrected when growth by a constant size per origin is implemented at initiation in steady-state growth (Methods S1–IV).

Another notable proposal for cell-size control in E. coli is a negative feedback imposed on cell size [68]. The hypothetical feedback exclusively relied on transient “oscillations” observed in the autocorrelation function (ACF) of cell size in experimental data and simulation data of an autoregressive model. However, it is well known that the ACF of the autoregressive model they used is an exponential function, in contradiction with the claimed oscillations. In other words, it is likely that the “oscillations” observed in both experimental and simulation ACFs are fortuitous, and caused by an insufficient sampling (approximately N=70 generations in each lineage) that fails to produce statistically meaningful autocorrelation coefficients.

CONCLUSION AND OUTLOOK

Altogether, we have shown that it is cell division [2, 3, 21, 25], not replication initiation [17, 37, 67], that drives cell-size homeostasis in bacteria. Initiation control is important in cell-size control, rather than cell-size homeostasis, because initiation defines unit cellular volume (or “unit cell”) so that the average cell size in any steady-state population is given by the sum of all unit cells [20]. From the cell-cycle control point of view, we showed that initiation and division are independently controlled in both E. coli and B. subtilis, thereby providing a conclusive answer to the long-standing question whether replication initiation regulates cell division in bacteria [34].

The mechanism underlying the adder phenotype for size homeostasis reduces to two biological hypotheses: (1) balanced biosynthesis of division proteins and precursors and (2) their accumulation to a threshold number in individual cells. In this work, we provided direct experimental evidence that support these two hypotheses for cell-size control and homeostasis. In our view, a next major question for the future is how a threshold model is implemented at the molecular level in division control and cell cycle control in general, while continuing a constructive dialog between quantitative phenomenological principles and mechanistic investigation.

The mechanism of adder has obvious implications for its applicability to other biological problems such as homeostasis of organelle content [56]. From an evolutionary point of view, cell-cycle dependent degradation of cyclins may explain why some eukaryotes show clear departure from adder by actively modulating physiological memory. But perhaps a more curious case is the mechanism of size homeostasis of the First Cells or synthetic cells, for which the simplicity of balanced growth makes adder an intriguing possibility.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Suckjoon Jun (suckjoon.jun@gmail.com).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Strains

E. coli

Strain background.

The E. coli strains used in all mother machine experiments are with either K-12 NCM3722 or K-12 MG1655 background. Both strains were sequenced and extensively tested in previous studies [20, 69, 70]. Strains with NCM3722 background were only used in steady-state growth, and strains with MG1655 background were used in both steady-state and oscillation experiments. Detailed information of strain genotypes are included in Tables S1 and S2.

Parent strains.

Some of the strains used in this study were constructed based on existing parent strains which have been tested and published. The original strain with the DnaN-YPet replisome marker was a kind gift of Rodrigo Reyes-Lamothe [71]. The strain for DnaA knockdown is based on the tunable CRISPR interference system developed in the Jun lab [32]. The DnaA overexpression strain used in the steady-state inhibition experiment is based on a strain with a plasmid carrying an extra copy of dnaA under P_lac promoter which was a kind gift of Tsutomu Katayama [72]. The DnaA overexpression strain used in the oscillation experiment is based on a similar strain with a plasmid carrying an extra copy of dnaA under P_lac promoter which was a kind gift of Anders Løbner-Olesen [43]. The construct of FtsZ-mVenus was a kind gift of Harold Erickson. In this construct, mVenus is inserted into the linker between domains of FtsZ, which has minimal effect on the function of FtsZ [54]. The system of P_tac::FtsZ was developed in Miguel Vicente’s lab [48, 51], and the strain VIP205 containing this system was a kind gift of William Margolin. We are grateful to the researchers mentioned above for these gifts of strains.

B. subtilis

Strain background.

The B. subtilis strains used in all mother machine experiments had JH642 background which is autoxophoic and requires supplementation of tryptophan, phenylalanine and threonine.

Parent strains.

The original strain with DnaN-mGFPmut2 replisome marker was developed in Alan Grossman’s lab [53] and was a kind gift of Paul Wiggins whose lab has conducted the cell cycle measurement using this strain [28].

See detailed strain information in Tables S1 and S2.

Growth media

For E. coli, we used MOPS or M9 minimal media supplied with different carbon sources and amino acids. For B. subtilis, S750 minimal media with different carbon sources and other supplements were used. The details of the media used are listed in the tables below.

List of growth media, carbon sources and supplements for E. coli.

Media name (as used in the text)	Buffer	Carbon source (v/w) concentration	Supplement
arginine	MOPS modified buffer	glucose 0.4%	no NH4Cl
glucose	MOPS modified buffer	glucose 0.2%	–
glucose + 12 a.a.	MOPS modified buffer	glucose 0.2%	see below
glycerol + 11 a.a.	MOPS modified buffer	glucose 0.2%	see below; no serine added
M9 acetate	M9 minimal buffer	sodium acetate 0.4%	see below

MOPS modified buffer

Components	Concentration
MOPS (MW 209.3)	40 mM
tricine (MW 179.2)	4.0 mM
iron(III) sulfate	0.1 mM
ammonium chloride	9.5 mM
sodium sulfate	0.276 mM
calcium chloride	0.5 μM
magnesium chloride	0.525 mM
sodium chloride	50 mM
ammonium molybdate	3 nM
boric acid	0.4 μM
cobalt chloride	30 nM
cupric sulfate	10 nM
manganese(II) chloride	80 nM
zinc sulfate	10 nM
potassium phosphate monobasic	1.32 mM

Supplements for glucose + 12 a.a.

Components	Concentration (μg/ml)
L-methionine	500
L-histidine	500
L-arginine	500
L-proline	500
L-threonine	500
L-tryptophan	500
L-serine	500
L-leucine	500
L-tyrosine	500
L-alanine	500
L-asparagine	500
L-aspartic acid	25

M9 minimal buffer

Components	Concentration
disodium phosphate	48 mM
monopotassium phosphate	22 mM
sodium chloride	8.6 mM
ammonium chloride	18.7 mM
magnesium sulfate	1 mM
calcium chloride	0.5 mM
vitamin B1	0.03 mM

List of growth media, carbon sources and supplements for B. subtilis.

Media name (as used in the text)	Buffer	Carbon source (v/w) concentration	Supplement
S750 mannose	S750 buffer	mannose 1%	see below

S7₅₀ buffer

Components	Concentration
MOPS (MW 209.3)	50 mM
Ammonium sulfate	1 mM
potassium phosphate monobasic	5 mM

Supplements

Components	Concentration
glutamate	6.8 mM
trisodium citrate	250 μM
iron(III) chloride	250 μM
tryptophan	50 μg/ml
phenylalanine	50 μg/ml
threonine	50 μg/ml

S7₅₀ metals

Components	Concentration
magnesium chloride	2 mM
calcium chloride	700 μM
manganese(II) chloride	50 μM
zinc chloride	1 μM
iron(III) chloride	5 μM
vitamin B1	1 mM
hydrochloride	20 μM

Experimental conditions and sample size

The detailed growth conditions, experimental parameters and samples size of each experiment included in this study are listed in Table S3.

METHODS DETAILS

Microfluidics

Mother machine microfluidic devices were used in this study to monitor single cell growth for 10–50 generations in both steady state and oscillation experiments. Syringe pumps (PHD Ultra, Harvard Apparatus, MA) were programmed to infuse fresh growth media into microfluidic device at either a constant rate or in an oscillatory manner.

Cell preparation

Before every time-lapse imaging, cells were picked from a single colony on an agar plate which was streaked no more than 7 days before use. The cells were inoculated into 1 mL lysogeny broth (LB) with proper selection antibiotics. After shaking for 12–18 hours at 30°C or 37°C in a water bath shaker, cells were diluted 1,000-fold into 2 mL of defined medium same as that used in the microfluidic experiments. After shaking at 37°C in the water bath till OD₆₀₀ = 0.1–0.4, cells were diluted again 100- to 1,000-fold into the same medium and shaken at 37°C in water bath till OD600 = 0.1–0.4. The cell culture was then concentrated 10- to 100-fold and injected into a microfluidic mother machine device via a 1 mL syringe. 0.5 mg mL⁻¹ BSA (Bovine serum albumin, Gemini Bio Products, CA) was added to the fresh growth media to reduce the adhesion of cells to the surface of microfluidic channels. The media were then added to 10 mL, 20 mL or 60 mL plastic syringes (BD) with 0.22 μm filters (Genesee Scientific, CA) for the time-lapse imaging. All imaging experiments were conducted at 37°C in an environmental chamber [3].

Microscopy and image acquisition

We performed simultaneous phase-contrast and epifluorescence imaging on an inverted microscope (Nikon Ti-E) with Perfect Focus 3 (PFS3), 100× oil immersion objective (PH3, numerical aperture = 1.45), Obis lasers 488LX or 561LS (Coherent Inc., CA) as fluorescence light source, and Andor NEO sCMOS (Andor Technology) or Prime 95B sCMOS camera (Photometrics). The laser power was 18 mW for 488 nm excitation and 17 mW for 561 nm, respectively. Exposure time was set between 50–200 ms. Imaging frequencies were calibrated at about 20 frames per doubling time such that no physiological effects on the cells were discernible.

Image processing

Cell segmentation, lineage reconstruction and cell dimension measurement

We developed custom imaging processing software using Python 2.7. The work flow is as follows. First, phase contrast images of each field-of-view (FOV) were sliced into small images each containing one growth channel of the mother machine device. Second, to enhance the contrast, the empty channels were subtracted from those containing cells in the same FOV. Third, subtracted images were thresholded using Otsu’s method to create a binary mask and then applied with morphological operations and a distance filter to create labeled markers. Markers were used to seed a watershedding algorithm on the subtracted images to create the segmented image. Lastly, lineages were constructed using a decision tree which tracked the time-evolution of the cell segments. The cell dimension was measured based on Feret diameter method: the cell length was calculated as the intercept of the cell’s long axis through the cell center and the outline of the segmented cell, and the cell width was calculated as the the mean of intercepts of the cell’s short axis through the cell quarter positions and the outline of the segmented cell.

Replisome foci analysis

The images of replisome markers were processed using the segmentation and lineage information from the phase contrast images of the same cells. Background subtraction was done by subtracting the mean value of multiple empty channels from those containing cells in the same FOV. Unfiltered fluorescence foci were identified as local maxima using a Laplacian of Gaussian method (blob_log function in Skimage v0.11.3). The localization for each identified focus was obtained using 2-D elliptic Gaussian fitting, and all foci were filtered again according to their peak-to-background value. The total fluorescence of each replisome focus was estimated as the total intensity of each blob. The distribution of fluorescence intensity of all foci was plotted and fitted with a double Gaussian distribution. The position of the second peak of the fitted Gaussian was typically two times that of the first peak, suggesting that two fluorescence foci were often spatially overlapping and undistinguishable due to the diffraction limit (Figure 1B). Therefore, a focus with higher probability of falling into the second peak region (integral of the intensity distribution between that foci intensity and the second peak > that of the first peak) was counted as two focus. The single-cell cell cycle analysis was carried out using a custom Matlab software. Intracellular positions and intensities of all foci in the same cells were plotted against time for the whole cell lineage. The start and end points of each foci trace were determined as the replication initiation and termination with respect to division cycles (Figure 1A, Figure S1).

FtsZ-mVenus concentration analysis

Fluorescence images of FtsZ-mVenus were used to estimate the total amount FtsZ per cell, the total concentration of FtsZ, the total fluorescence of the Z-ring and the cytoplasmic concentration of FtsZ. Compared to the replisome marker images, extra calibration of systematic errors was done as follows. (1) We corrected the photobleaching effect by truncating the time points when the average fluorescence of cells have not reached steady state. (2) The illumination of the laser was often non-uniform across the FOV. The profile of illumination was obtained from the average intensity of all cells in the same FOV. The fluorescence intensity of each cell was thus calibrated according to the profile and their position in the FOV. (3) The FOV-to-FOV variations were typically less than 5%, so no calibration was applied. The first 5–10 generations of the time-lapse images were discarded to ensure that photobleaching reaches stationarity of the timelapse data. The total fluorescence of FtsZ per cell was used to estimate the total amount FtsZ per cell. The total fluorescence normalized by cell volume was used to estimate the total concentration of FtsZ. The amount of FtsZ in the mid-cell area was quantified by integrating the fluorescence intensity within a fixed box with dimensions of 1 μm along cell long-axis and 1.5× cell width along short axis. This area is centered at max intensity position of the line profile along cell long-axis. This quantity was used as an approximation of the total fluorescence in the Z-ring. The cytoplasmic concentration of FtsZ was estimated as the total fluorescence within an area of the same size centered at a cell-quarter position along the cell long-axis. The cytoplasmic concentration of FtsZ was shown to be much higher than the cellular autofluorescence. We showed this by co-growing and imaging the FtsZ-mVenus strain and wildtype parental strain in the same mother machine device. The autofluorescence level of the wild type strain is less than 10% of the cytoplasmic FtsZ-mVenus fluorescence (Figure S5D).

Stochastic simulations of the Helmstetter-Cooper model

To investigate what determines cell-size homeostasis we developed stochastic simulations of the Helmstetter-Cooper cell cycle model (Cooper and Helmstetter 1968; Donachie 1968). In this model, three coarse-grained physiological parameters describe the progression of the cell cycle and cell size: the growth rate λ, the cell size per origin at replication initiation s_i, and the length of cell cycle τ_cyc = C+D, namely the duration that spans one complete round of replication (C period) and division that corresponds to replication termination (D period). We introduced stochasticity to these parameters (λ, s_i, τ_cyc) and numerically probed the resulting behavior of cell-size homeostasis (Figure 1C). See more details in Methods S1–I. The stochastic fluctuations constituted a 9-dimensional physiological space consisting of and three coefficient-of-variations (CVs), three cross-correlations and three autocorrelations (Figure 2A), with each physiological dimension representing specific biological constraints. For instance, positive autocorrelations in the growth rate λ mean that on average fast-growing mother cells produce fast-growing daughter cells. When these refinements were added, our stochastic simulations self-consistently reproduced the experimentally observed adder behavior for all tested growth conditions without any adjustable parameters (Methods S1–I). In Figure 2A, we set out to systematically vary physiological parameters along all nine dimensions to probe the adder behavior. Each simulation generated a lineage of 10,000 cells. The adder correlation ρ(Δ_d, S_b) was defined as the Pearson correlation between the variables Δ_d and S_b in the simulated lineage. We adopted the same definition for the initiation adder correlation ρ(δ_i, s_i). Eventually, we found that deviations in the autocorrelation of initiation size per ori s_i from 0.5 significantly affected the division adderness. In contrast, deviations from adder resulting from other perturbations were weaker or less systematic, reinforcing the general robustness of adder observed in our inhibition experiments (Figure 1D). This sensitivity of adder to s_i autocorrelation is clearly seen in the fraction of physiological space represented by adder (Figure 2A). It is also intuitive since in the Helmstetter-Cooper model, division timing is regulated by chromosome replication initiation. As reference physiological values, we used experimental measurements obtained for strain NCM3722 in slow growth condition (MOPS minus NH₄Cl, 0.4 % glucose, 5 mM arginine). Namely, where appropriate we parametrized the joint probability distribution using the mean and coefficient-of-variations:

Variable	λ	τcyc	Si
Mean	0.693	0.7	1
CV	15%	15%	10%

and the Pearson cross-correlations and autocorrelations:

Pearson correlation	Value
ρ(λ,τcyc)	−0.5
ρ(λ,Si)	−0.2
ρ(τcyc,Si)	−0.3
ρ(λ(n+1),λ(n))	0.5
ρ(τcyc(n+1),τcyc(n))	0.3
ρ(Si(n+1),Si(n))	0.5

Note that we chose the generation time as unit of time and the cell size per origin at initiation as unit of volume. For this particular condition, the generation time was ln(2)/〈λ〉= 112 minutes and the cell size per origin at replication initiation was s_i = 0.30 μm³.

Analysis of FtsZ oscillation experiment results

Let us consider a single cell, experiencing a switch in induction, corresponding to a change of steady-state concentration from c* to c**. Denoting S_ind the cell size reached when the switch in induction occurs, by applying Eq. 22 and Eq. 23 from the Methods S1–II, we obtain:

$$S_{\text{d}}-S_{\text{b}}={\Delta }_{\text{d}}^{**}-\left(S_{\text{ind}}-S_{\text{b}}\right)\left(\frac{{\Delta }_{\text{d}}^{**}}{{\Delta }_{\text{d}}^{*}}-1\right),$$

where Δ_d* = N₀/(2c*) and Δ_d** = N₀/(2c**) are the added size in each induction phase. Assuming exponential elongation of cell size at the rate λ, we may express:

$$S_{\text{ind}}-S_{\text{b}}=S_{\text{b}}\left(e^{\lambda a_{\text{ind}}}-1\right),$$

where a_ind is the age of the cell when the switch in induction occurs. We therefore obtain for the conditional average:

$$\langle S_{\text{d}}-S_{\text{b}}|S_{\text{b}}\rangle ={\Delta }_{\text{d}}^{**}-A\left(\frac{{\Delta }_{\text{d}}^{**}}{{\Delta }_{\text{d}}^{*}}-1\right)S_{\text{b}},$$

where A = 〈e^λa - 1〉, and therefore A > 0.

Effect of ClpX on cell size homeostasis

In the presence of ClpX, we consider that division proteins are actively degraded at a rate μ. Denoting N the copy number of division proteins, the balanced biosynthesis of division proteins is modified to:

$$\frac{\text{d}N}{\text{d}t}=c^{*}\frac{\text{d}S}{\text{d}t}-\mu N.$$

Assuming that the cell volume grows exponentially at the rate λ, the previous ODE can be solved, and one obtains the following relation between copy number and cell volume:

$$S\left(t\right)=\frac{1}{c^{*}}\left(1+\frac{\mu }{\lambda }\right)\left(N\left(t\right)-N_{\text{b}}{e}^{-\mu t}\right)+S_{\text{b}}{e}^{-\mu t},$$

where N_b = N(t=0) is the copy number at cell birth and S_b = S(t=0) is the cell volume at cell birth. We assume even partitioning of division proteins at division, so that their number at birth is half the threshold: N_b = N₀ / 2. We can now get some insight on cell size homeostasis by considering the two limiting cases (1) μ ≪ λ and (2) ≫ λ. In case (1), we obtain to order zero in μ/λ that S_d - S_b = N₀/(2c*), which is the adder model. On the contrary in case (2), we obtain asymptotically: S_d = (μ/λ)·N₀/c*, which is the sizer model. In summary, the cell size behavior transitions from the adder model to the sizer model when active degradation of division proteins is introduced.

QUANTIFICATION AND STATISTICAL ANALYSIS

The error bars in all main figures and supplemental figures represent standard error mean of binned data. In the correlation plots in Figures 3, 4 and 7, the boundary of shaded area indicate 95% confidence interval of linear fit coefficients assuming the measurement errors are normally distributed and centered at zero. All the fittings were performed in Igor Pro 6 (Wavemetrics, Inc.). The typical sample size of each experiment is about 10³ cell. detailed sample size of each experiment is listed in Table S3. In Figure 7B, the significance of linear correlation (p-value < 0.001) was estimated using Student’s t test in Matlab. In the simulations (see Figure 2 and Methods S1–I), Pearson coefficient was used to quantify both cross-correlations and mother-daughter autocorrelations.

DATA AND SOFTWARE AVAILABILITY

We provide a dataset of single-cell growth and cell cycle as Data S1. We also would like to share all other data upon request.

Methods S1. Detailed descriptions of the theory, simulation, and calculations for models of cell-size homeostasis, Related to STAR Methods and Figures 2–6.

This document contains detailed descriptions of single-cell stochastic simulation of the Helmstetter-Cooper model, the theory for the threshold model in balanced growth, detailed calculations for the perturbed cell size homeostasis under oscillatory induction of division and initiation initiator proteins, and discussions on other related models.

Data S1. Single-cell data of physiological measurements in different steady-state growth conditions, Related to Figures 1, 2, S1 and S2.

This dataset includes physiological parameters such as cell size, growth rate and timing of cell cycle measured from steady-state growth for different strains and nutrient conditions.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial Strains
See Table S1
Chemicals, Peptides, and Recombinant Proteins
Chloramphenicol	Sigma	Cat#C0378–5G
Fosfomycin	Sigma	Cat#P5396–5G
Oligonucleotides
Primers for replacing ftsZ with ftsZ-mVenus Forward: ATGTTTGAACCAATGGAACTTACC	This paper	N/A
Primers for replacing ftsZ with ftsZ-mVenus Reverse: ACGTGTCTGGTCAACGAGCA	This paper	N/A
sgRNA targeting sequence for ClpX: TCCGTGTATATCTGCGACGA	This paper	N/A
Software and Algorithms
Matlab R2015b	Mathworks, Inc.	RRID:SCR_001622
Anaconda Python 2.7	Anaconda, Inc.	https://www.anaconda.com/distribution/
NIS-Elements	Nikon Instruments Inc.	RRID:SCR_014329
Other
Nikon Ti-E inverted microscope	Nikon Instruments Inc.	Cat#MEA53100
Nikon Perfect Focus system 3	Nikon Instruments Inc.	Cat#MEP59391
Obis lasers 488LX	Coherent, Inc.	Part#1236444
Obis lasers 561LS	Coherent, Inc.	Part#1230949
Andor NEO 5.5 sCMOS camera	Oxford Instruments	Model#DC-152Q-C00-FI
Prime 95B sCMOS camera	Photometrics	https://www.photometrics.com/products/scmos/prime95B
PHD ULTRA Syringe Pump	Harvard Apparatus	Cat#70–3007

HIGHLIGHTS.

• The adder requires accumulation of division proteins to a threshold for division.

• The adder requires constant production of division proteins during cell elongation.

• In E. coli and B. subtilis, initiation and division are independently controlled.

• In E. coli and B. subtilis, cell division exclusively drives size homeostasis.