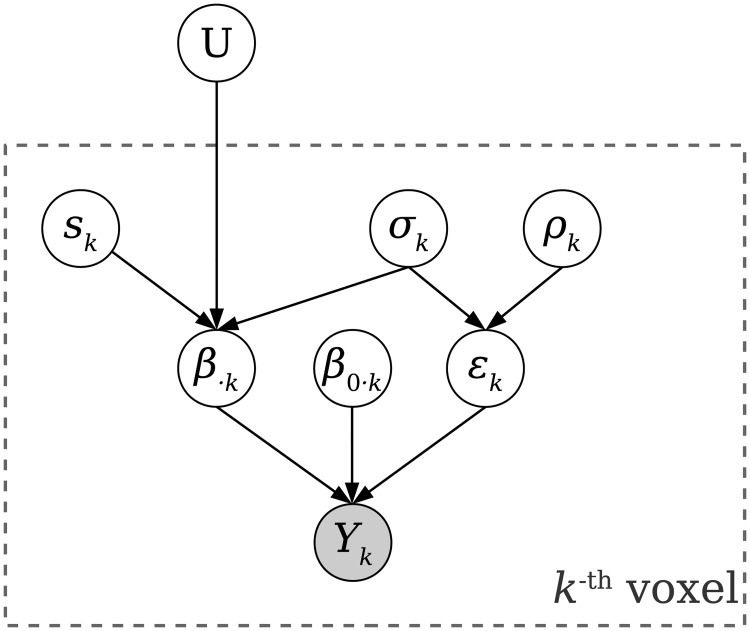
Fig 2. Generative model of Bayesian RSA.

The covariance structure U shared across all voxels in an ROI is treated as a hyper-parameter of the unknown response amplitude β. For voxel k, the BOLD time series Y_k are the only observable data. We assume Y_k is generated by task-related activity amplitudes β_⋅k (the k-th column of β), intrinsic fluctuation amplitudes β_0⋅k and spatially independent noise ϵ_k: Y_k = Xβ_k + X₀ β_0⋅k + ϵ_k, where X is the design matrix and X₀ is the set of time courses of intrinsic fluctuations. ϵ_k is modeled as an AR(1) process with autocorrelation coefficient ρ_k and noise standard deviation σ_k. β_⋅k depends on the voxel’s pseudo-SNR s_k and noise level σ_k in addition to U: β_⋅k ∼ N(0, (s_k σ_k)² U). By marginalizing over β_⋅k, β_0⋅k, σ_k, ρ_k and s_k for each voxel, we can obtain the likelihood function p(Y_k|X, X₀, U) and search for U which maximizes the total log likelihood $\mathbf{\text{log}}\mathit{p}\left(\mathbf{Y}\right|\mathbf{X},{\mathbf{X}}_{\mathbf{0}},\mathit{U})={\sum }_{\mathit{k}}^{{\mathit{n}}_{\mathit{V}}}\mathbf{\text{log}}\mathit{p}\left({\mathit{Y}}_{\mathit{k}}\right|\mathbf{X},{\mathbf{X}}_{\mathbf{0}},\mathit{U})$ of the observed data Y for all n_V voxels. The optimal $\widehat{\mathit{U}}$ can be converted to a correlation matrix, representing the estimated similarity between patterns.