Diffusion transport of a 2D nanosheet sandwiched inside a cell membrane can exhibit the transition from Brownian to Lévy dynamics.
Abstract
The transport of nanoparticles at bio-nano interfaces is essential for many cellular responses and biomedical applications. How two-dimensional nanomaterials, such as graphene and transition-metal dichalcogenides, diffuse along the cell membrane is, however, unknown, posing an urgent and important issue to promote their applications in the biomedical area. Here, we show that the transport of graphene oxides (GOs) sandwiched inside cell membranes varies from Brownian to Lévy and even directional dynamics. Specifically, experiments evidence sandwiched graphene–cell membrane superstructures in different cells. Combined simulations and analysis identify a sandwiched GO–induced pore in cell membrane leaflets, spanning unstable, metastable, and stable states. An analytical model that rationalizes the regimes of these membrane-pore states fits simulations quantitatively, resulting in a mechanistic interpretation of the emergence of Lévy and directional dynamics. We finally demonstrate the applicability of sandwiched GOs in enhanced efficiency of membrane-specific drug delivery. Our findings inform approaches to programming intramembrane transport of two-dimensional nanomaterials toward advantageous biomedical applications.
INTRODUCTION
The dynamic nature of cell membranes is essential for cellular functioning (1–4). As the basis of a cell membrane, the lipid bilayer provides a compartmentalized matrix within and on which nanoscale particles, such as proteins, macromolecules, and therapeutic nanocarriers, are in a constant state of motion and redistribution (5–7). These dynamic processes play a critical role in cellular mechanisms encompassing metabolism, endocytosis and secretion, differentiation, locomotion, and signal transduction (8–12). Understanding the diffusive dynamics of nanoparticles on the cell membrane is thereby crucial for their efficient and safe biomedical applications. Experiments (13, 14) and theoretical models (15, 16) have been intensively proposed to examine and explain the diffusive transport of spheres or other three-dimensional (3D) nanoparticles on the cell membrane. It is, however, less well understood how 2D nanomaterials, such as graphene and transition-metal dichalcogenides, transport along the cell membrane.
As the most well-known 2D nanomaterials, graphene and its derivatives have a range of unique and versatile physical and chemical properties (17, 18). The tunability of the properties is perhaps unprecedented among other nanomaterials, offering immense design capabilities that may enable a considerable number of applications of these emerging nanomaterials in the cutting-edge fields of biological and medical science (19–21). Biomedical applications for graphene are attracting interest from academics and industrial partners aiming to develop next-generation medical devices and therapies (22, 23). Yet, the detailed dynamical process and underlying molecular mechanism of how graphene transports on the cell membrane remain unclear, posing an urgent and important issue to promote their applications in biomedicine. This gap in our understanding is largely attributable to the intrinsically high complexity of the interaction states between graphene and the membrane (24–27). To definitely elucidate the diffusion dynamics of graphene at such unconventional bio-nano interfaces, here, we focus on a unique state of graphene–cell membrane interaction, that is, the sandwiched graphene–cell membrane superstructure (28), where the graphene oxide (GO) is hosted in the hydrophobic interior of the lipid bilayer as illustrated in Fig. 1A. Despite needing to be experimentally validated, this is the first graphene–cell membrane interaction state predicted by simulations (28, 29). The GO encapsulation makes this superstructure absolutely distinct from the basic features of interfacial transport of membrane-trapped 3D nanoparticles (15, 29, 30) and may allow diverse approaches for novel biomedical applications.
Fig. 1. Experimental evidence of the sandwiched graphene membrane superstructure and the following cell responses.
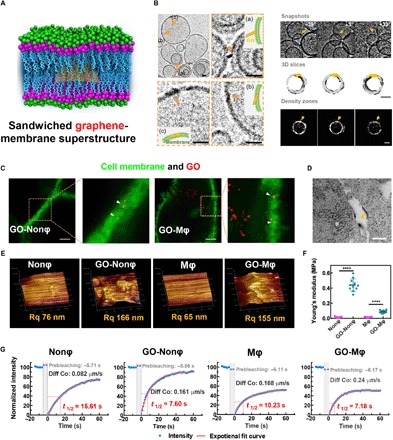
(A) Cartoon illustrating the superstructure integrating GO inside the cell membrane. (B) Cyro-TEM images (left) and tomography views (right) of the lipid vesicles in the presence of GO. Scale bars, 20 nm. The sandwiched graphene-membrane superstructure was formed via three possible processes: primary contact, perpendicular/slant insertion, and final settlement. The lipid vesicle in the presence of a GO nanosheet (as indicated by the arrows) shows higher mass density. (C) Super-resolution confocal images showing the GO sandwiched in the membrane of different cells (macrophage Mφ and nonphagocyte Nonφ). The green fluorescence indicates the phospholipid bilayer membranes bound by the lipid probe [3,3′-dioctadecyloxacarbocyanine perchlorate (DiO)], while the false-colored red spots indicate the GO signal. Yellow spots indicate the sandwiched GO in the membrane. Scale bars, 1 μm. (D) TEM images exhibiting the GO-sandwiched superstructure. The GO is marked by the yellow triangle. Scale bar, 100 nm. (E) AFM images and the roughness index of the cell membrane with embedded GOs. (F) The Young’s modulus indicating the rigidity change of cell surface upon GO interaction. (G) FRAP analysis showing the fluidity of the membrane lipids. Diff Co and the t1/2 represent the diffusion coefficient and half-time for the fluorescence recovery of membrane after photobleaching, respectively.
In the present work, we first provide experimental evidence of sandwiched graphene–cell membrane superstructures in different cells. By combining simulations and experiments, we find that the translational transport of GOs sandwiched inside cell membranes changes from Brownian to Lévy and even directional dynamics, governed by various states of a sandwiched GO–induced pore in the leaflet of the membrane. A mechanistic interpretation of the emergence of Lévy and directional dynamics is realized by quantitatively correlating the simulations to an analytical model that is developed to rationalize the regimes of the membrane-pore states spanning unstable, metastable, and stable cases. Last, both experiments and simulations point to the enhanced efficiency of membrane-specific drug delivery for the sandwiched GO. This work elucidates the translation or diffusion dynamics of cell membrane–embedded 2D nanomaterials and discloses the basic nature of the mechanism of such intramembrane transport dynamics with programmable directional persistence.
RESULTS
Experimental evidence of the sandwiched graphene–cell membrane superstructure
To enable experimental validation of the simulations (27, 28), we herein used GOs with ultrasmall size (fig. S1) and a certain oxidization degree (26.1%) (31, 32), which allows us to provide direct evidence of the sandwiched graphene-membrane superstructure in a cellular level. To provide evidence of the sandwiched superstructure, we use the cryogenic transmission electron microscopy (cryo-TEM) technique and visualize the GO membrane in a fully hydrated medium, close to native state. As shown in the images and tomography views (Fig. 1B and figs. S2 and S3), darker lines (with higher mass density, as shown in Fig. 1B and fig. S3C) appear within the lipid bilayer membrane upon exposure to GO nanosheets, which is quite different from that of the blank lipid vesicles with homogeneous density (figs. S2A and S3, D to G). Moreover, the sandwiched structure of GO in the lipid bilayer membrane can be reconfirmed at different detection angles (Fig. 1B and figs. S2C and S3A) and particularly through the 3D views of the tomography snapshots in Fig. 1B and fig. S3. We can thereby identify the formation process including the primary contact, perpendicular/slant insertion, and final settlement within the membrane (Fig. 1B and fig. S2B), consistent with our previous simulations (27).
Together with the cyro-TEM proof, the super-resolution confocal images (Fig. 1C) and TEM images (Fig. 1D and fig. S4) also provide in vitro evidence for GO-based superstructures in the cell membrane. GO nanosheets are found to be hosted inside the membrane of a nonphagocyte (Nonφ, 4T-1). A similar phenomenon can also be identified on a macrophage (Mφ, J774A.1) (Fig. 1C), although some GOs are internalized into the cell due to the active phagocytosis (fig. S5A).
Although such a GO-sandwiched structure has very little effect on the leakage of cell membrane (fig. S5B), we observe its notable influence on the membrane morphologies using an atomic force microscope (AFM). Compared with untreated cells, the GO insertion results in a wavier surface with a higher roughness index Rq (root-mean-square roughness) (Fig. 1E), especially for the Nonφ. The GO-Nonφ group also induces a 10-fold increase in membrane rigidity (indicated by Young’s modulus), which is much larger than that of the GO-Mφ group (Fig. 1F). In agreement with our following simulations (fig. S18), membrane fluidity can be recognized to evidently increase by using the fluorescence recovery after photobleaching (FRAP) technique (Fig. 1G and fig. S5C). For example, the diffusion coefficient (Diff Co) of the GO-Nonφ group is almost twice as much as that of the untreated group, and the half-time (t1/2) of fluorescence recovery correspondingly reduces from 15.61 to 7.60 s for the GO-Nonϕ group. Together, the experimental data demonstrate the existence of the sandwiched graphene-membrane superstructure and reveal its nontrivial effects on membrane properties including roughness, rigidity, and fluidity.
Simulations reveal Lévy and directional dynamics of the sandwiched GO
In the sandwiched graphene-membrane superstructure, the lipid bilayer of the membrane almost fully isolates the embedded GO from the external solution, making it difficult to directly characterize its intramembrane diffusion. To accomplish such a challenging task, we perform coarse-grained molecular simulations where the mesoscopic simulation technique (33–37), including explicit solvent beads, has been fully proved to faithfully reproduce all key properties of the self-assembling fluid bilayer membrane and the GO-membrane interactions (see Materials and Methods, section S1, and fig. S6 for more details) (27, 29). We start from obtaining the GO-sandwiched structure by simulating the interaction between GO with edge length a = 4.9 nm and a square patch of the lipid bilayer membrane, where the interaction parameter between GO and lipid tails, χGT, can be changed to reproduce different oxidization degrees or chemical modifications of the GO (see Materials and Methods for more details and figs. S7 and S8 and movies S1 and S2).
Three typical trajectories of the center of mass (COM) of the sandwiched GO are illustrated in Fig. 2 (A to C), where the attraction between GO and lipid tails is gradually reduced, mimicking, for example, the increased oxidization degree of the GO (see movies S3 to S5 for detailed dynamics). Note that, for each analysis, the COM of the associated bilayer leaflet is subtracted from the trajectories of the GO to remove effects of COM motion of the membrane. For strong GO–lipid tail attraction (χGT = 1.43), the diffusion of GO within the membrane undergoes Brownian dynamics, as confirmed by the stochastic trajectory (Fig. 2A) and the Gaussian distribution of displacements (fig. S9A). In this case, the translational diffusion coefficients of the GO can still be well described by the Saffman-Delbrück model (15) that is widely used to quantitatively understand the Brownian diffusion of proteins trapped in the membrane (fig. S9B). Upon reducing GO–lipid tail attraction to χGT = 7.15, the sandwiched GO alternatively performs persistent walks and local jiggling, which are schematically indicated by arrows and dashed ovals, respectively, in Fig. 2B. To reveal the inner nature of this unusual randomness, we used a wavelet-based method to rapidly separate persistent segments from random jiggling (38, 39), as shown in the inset of Fig. 2B (section S1). This allows us to calculate the time-averaged mean-square displacement (MSD) of both these segments and thereby identify that the jiggling segment is invariably Fickian while the persistent segment is invariably superdiffusive (Fig. 2D).
Fig. 2. Transition of diffusion patterns of the sandwiched GO from Brownian to Lévy and even directional dynamics.
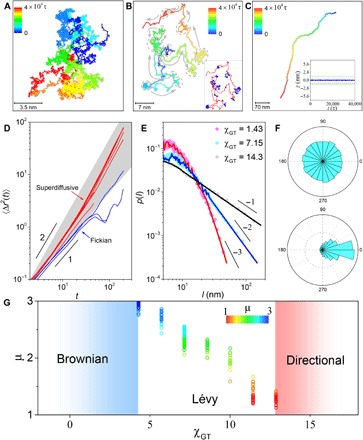
(A to C) Representative trajectories tracked for 4 × 104 τ, when the interaction parameter between GO and lipid tails, χGT, is (A) 1.43, (B) 7.15, and (C) 14.3. Colors denote the time lapse of each trajectory. In (B), arrows and dashed ovals indicate alternating persistent segments and jiggling periods, respectively, which are quantitatively identified by wavelet analysis shown in the inset. Inset of (C): The averaged position of GO in the z axis as a function of time, where z = 0 represents the middle of the membrane. (D) Time-averaged mean square displacement 〈Δr2(t)〉 as a function of lag time on log-log scales for persistent (red) and jiggling (blue) segments of the trajectory at χGT = 7.15. (E) The probability distribution of step length, l, on log-log scales, showing exponential statistics at χGT = 1.43 but power-law statistics with slope −2 at χGT = 7.15 and −1 at χGT = 14.3. (F) Statistic distributions of angles between neighboring persistent segments for the trajectories at χGT = 7.15 (top) and 14.3 (bottom). (G) The plot of the exponent defining the power-law distribution of step length, μ, against χGT for the systems exhibiting Lévy dynamics. The step-length distribution from about 50 sets of simulated trajectories at each χGT is summarized. The color bar encodes the value of μ.
Extending the analysis, we denote the length of the persistent or jiggling segment as l. Figure 2E shows the plots of relative probability against l on log-log scales for various GO–lipid tail interactions. In sharp contrast to the exponential distribution for the Brownian dynamics at χGT = 1.43, the distribution at χGT = 7.15 exhibits a power-law slope of μ = −2, determined from maximum likelihood estimation (section S1) (40). In addition to the uniformly distributed turning angles between neighboring persistent segments (Fig. 2F and fig. S10), we can conclude that the transport of the sandwiched GO upon reduced GO–lipid tail attraction follows the landscape of Lévy walk, where the distribution of step length is heavy-tailed with slope μ satisfying −3 < μ < −1 (41). This result is also confirmed by analyzing the displacement probability distributions, the non-Gaussian parameters, the displacement autocorrelation function, the MSD of the whole trajectories, and the relative standard deviation of MSDs (fig. S11) (8). However, further decreasing χGT to 14.3 resulted in a change in isotropy. The transport of the sandwiched GO instead prefers nontrivial directionality, as confirmed by the directional trajectory (Fig. 2C), the biased distribution of turning-angle statistics (Fig. 2F), and the power-law slope of μ = −1 for the l distribution (Fig. 2E) (42).
As the most efficient random search strategy, Lévy walks are broadly found in nature (40, 43). The aforementioned results hint that such a prominent strategy might also be adopted by cells for efficient transport of nanoparticles along the cell membrane. To assess the detailed range for the emergence of Lévy dynamics, we systematically examine the power-law slope of μ by walking through the parameter space of χGT. This leads to the 2D diagram as shown in Fig. 2G, which summarizes the outcomes of about 50 independent simulation runs at each value of χGT. Specifically, below χGT = 4.50, the transport reverts to Brownian; above χGT = 12.87, the transport favors statistic directionality. Within a broad range in between, Lévy walk emerges.
Sandwiched GO–induced hemi-pore in the leaflet of the cell membrane
To understand the transition of such transport patterns, we examine the details of the sandwiched graphene–cell membrane superstructure in response to various GO–lipid tail interactions. The GO is found to remain within the center of the lipid bilayer during the whole simulation period and in the current range of χGT (inset of Fig. 2C), ruling out the contribution from the GO fluctuation normal to the membrane plane. Changing the GO geometry from a square shape to a circular one, as well as enlarging the membrane size, we find that GO geometry has a trivial effect on the transition of the transport patterns (figs. S12 and S13). These results inspire us to turn to focusing on the detailed structure of the membrane integrating GO. For this purpose, a simple indicator of the integrity of the membrane is obtained by counting the number of GO beads that contact solvent, N. Figure 3A shows the probability distributions of N, which summarize every time within the whole simulation period (5 million time steps) at each χGT (fig. S14, A to D). The nonzero values of N suggest that the membrane integrity cannot hold, especially for a reduced attraction between GO and lipid tails. At corresponding values of χGT, a hemi-pore (for brevity, “hemi-” is omitted in the rest of this paper) can be identified in the leaflets of the bilayer membranes and just above the GO plane (fig. S15) (44).
Fig. 3. Combined simulations and experiments demonstrate the sandwiched GO–induced pore in the leaflets of cell membranes.
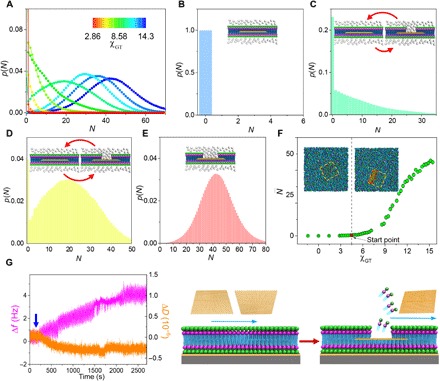
(A) Probability distribution of the number of GO beads contacting solvent, N, during a simulation period of 4 × 104 τ, p(N), at a series of χGT encoded by the color bar. (B to E) p(N) at various χGT: (B) 1.43, (C) 7.15, (D) 10.01, and (E) 14.3. N indicates the size of the pore in the leaflet of the membrane, as schemed by the insets. (F) The time-averaged N in the whole period, , as a function of χGT. The red circle in the plot marks the start point from which is above 0 and pore occurs. The insets are two snapshots showing the typical GO-sandwiched structures without (left) and with (right) a pore, where the dashed squares mark the contour of GO and the red outline displays the pore. (G) QCM data (frequency, Δf; dissipation, ΔD) during the interaction between GO and the lipid bilayer, as schematically illustrated by the right diagram.
A close examination of the N distributions in Fig. 3A leads to an intriguing observation: All the distributions of N can be classified into four types based on differences in their maxima, as shown in Fig. 3 (B to E). For a strong GO–lipid tail attraction, N remains at zero, demonstrating that no pore occurs (Fig. 3B). Upon reducing GO–lipid tail attraction, the maximum remains at N = 0 along with a few nonzero N, indicating a reversible transition between the structures without and with a pore during GO transport (Fig. 3C). In this case, the former dominates the transition, causing the unstable state of the pore. With further reducing χGT, the transition between both structures almost balances, as described by the formation of the other maximum at nonzero N (Fig. 3D). Here, a small perturbation may readily trigger the transition between both structures, suggesting the metastable nature of the pore (42). When χGT is large enough, only the maximum at nonzero N exists so that the pore reaches the stable state (Fig. 3E). The remarkable dependence of these diverse pore states on χGT corroborates that such a pore is substantially induced by the sandwiched GO. Particularly, plotting the time-averaged N within the simulation period, , against χGT confirms that the occurrence of the pore starts from χGT = 4.50 (Fig. 3F).
To experimentally verify the sandwiched GO–induced pore, we constructed a special quartz crystal microbalance (QCM) chip (fig. S14E) and measured the structure changes (dissipation, ΔD) and the mass changes (frequency, Δf) during the interaction between GO and the lipid bilayer (37). As shown in Fig. 3G, the addition of GO has little effect on the ΔD. In notable contrast, the gradually increased Δf suggests that the mass on the chip decreases with the interaction time. In light of the above simulation results, this can be attributable to loss of lipid molecules during the insertion process of GO.
Analytical model of the sandwiched GO–induced pore
To complement the simulations and provide a fundamental insight into various states of the sandwiched GO–induced pore, we develop a model that is amenable to analytical solutions (see Materials and Methods and section S2 for details). As illustrated by the schematic diagram in Fig. 4A, the energy of the membrane tension induced by the interaction between GO and lipid tails drives the pore formation, which, however, is opposed by the energy of the line tension that creates the edge of the pore. This leads to a critical relationship between the energy cost of pore formation, ER, and the radius of the pore, R, as defined by Eq. 1 and plotted in Fig. 4B. For relatively weak GO–lipid tail repulsion with small interaction energy density Ka, ER increases monotonically with R, indicating that the pore cannot occur or is unstable. As Ka increases, there exists a local energy maximum at smaller R and a local energy minimum at larger R, and the energy difference between them results in an energy barrier, ΔE, for the annihilation of a formed pore. The detailed values of both of these points can be analytically determined, as indicated by the dashed curves in Fig. 4B (see also section S2 and fig. S16). When Ka is not too high, the energy barrier is lower and may be readily overcome; thereby, the pore is metastable in nature. If Ka is large enough, then the local energy minimum tends to be global and ΔE becomes so high that the pore reaches the stable state. In short, compared with the results of Fig. 3 (A to E), these energy evolution profiles reproduce various pore states observed in the simulations.
Fig. 4. Analytical model of the sandwiched GO–induced pore.
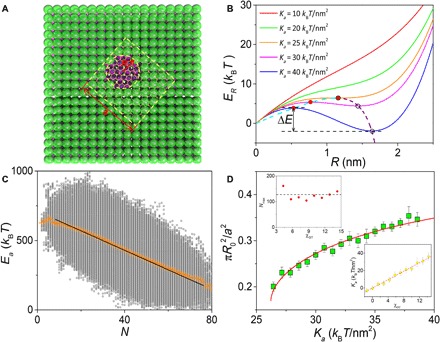
(A) Schematic representation of the detailed structure and parameters considered in the analytical model of the sandwiched GO–induced pore. (B) The energy cost of pore formation, ER, as a function of pore radius at different Ka, i.e., the interaction energy density of lipid tails with GO. The solid and hollow circles at each plot mark the local maximum and the local minimum of ER, respectively. The dashed cyan and purple curves give the analytical solutions of both of these types of points, which meet at the transition point with Ka = 25 kBT/nm2. (C) Plot of GO–lipid tail interaction energy, Ea, versus the number of GO beads contacting solvent N, where χGT = 10.01. Averaged from 5 million time steps (raw data obtained from simulation results and shown as gray circles), the yellow crosses have the linear fitting indicated in the figure. (D) The ratio between the most probable pore (pore at the energy minimum) area and GO area as a function of Ka. The green points and red curve represent the results from the simulation and analytical model, respectively. Top inset: The maximum of GO beads contacting solvent, Nmax, remains almost unchanged with increasing χGT. Bottom inset: The plot of Ka used in the analytical model versus χGT used in the simulation, approximating a linear fitting as indicated by the dashed red line.
For further quantification, we first derive the relationship between N and GO–lipid tail interaction energy, Ea, as described in Eq. 4 (see Materials and Methods). By applying this model to fit the averaged Ea-N data within a whole simulation period (Fig. 4C), the values of Ka and Nmax, the maximum of GO beads contacting solvent, can be obtained for a certain χGT. Repeating this process with a series of χGT allows us to determine the Ka-χGT relationship, as well as almost invariant Nmax, which highlights the consistency of the model (insets of Fig. 4D and fig. S17). Meanwhile, the systematic simulations give the area change of the most probable pore with respect to χGT. On the basis of Eq. 2, the dependence of the pore area on Ka can also be analytically obtained, which agrees exactly with the simulation results in light of the Ka-χGT relationship (Fig. 4D). Such a close agreement underscores a quantitative support for the correlation between our analytical model and simulations.
Mechanisms of the emergence of Lévy and directional dynamics
Having established the states of the sandwiched GO–induced pore and the quantitative relations between simulations and the analytical model, we now provide a refined picture of the mechanism underpinning the transition of transport patterns from Brownian to Lévy and even directional dynamics. First, we determine the precise boundaries of four different regimes of the pore states by combining simulations and theoretical analysis (Fig. 5A). The details regarding this aspect can be found in section S2. Briefly, the boundary between regimes I (without pore) and II (unstable state) occurs at Ka = 10 kBT/nm2 (χGT = 4.50) as determined by simulations (Fig. 3F). For the boundary between regimes II and III (metastable state), it can be obtained by either the crossover in the curve describing Ka dependence of the most probable pore area from simulations or the transition point in the ER-R curves from theoretical analysis (see Fig. 4B, Materials and Methods, and fig. S16). The boundary between regimes III and IV (stable state) is determined by the occurrence of an energy barrier equal to thermal energy, i.e., ΔE = 1 kBT, where Ka = 30 kBT/nm2 (χGT = 12.43) (Fig. 5B).
Fig. 5. Correlation between diffusive dynamics and membrane-pore states elucidates the mechanisms of Lévy walk and directional motion of sandwiched GO.
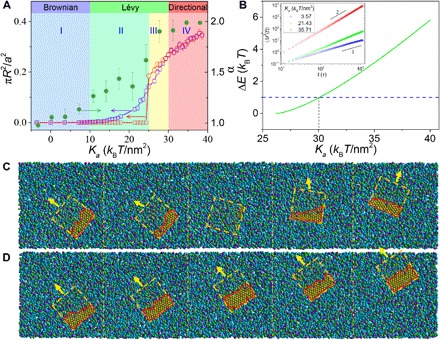
(A) The area ratio between pore and GO and the diffusion exponent, α, as a function of Ka. The red and blue curves depict the cases of the most probable pore area and the averaged pore area, respectively. The shaded regions divide four regimes of the membrane-pore states, where the colors correspond to those adopted in Fig. 3 (B to E). (B) The energy barrier in the ER-R curve, ΔE (Fig. 4B), as a function of Ka. The dashed blue line plots the thermal energy, 1 kBT. Inset: Time-averaged mean square displacement 〈Δr2(t)〉 as a function of lag time on log-log scales for various Ka, where the slopes give α. (C and D) Successive stages of a sandwiched GO exhibiting Lévy walk at χGT = 10.01 (Ka = 25.29 kBT/nm2) (C) and directional motion at χGT = 14.3 (Ka = 34.74 kBT/nm2) (D). The dashed squares mark the contour of GO, the red outlines display the pore induced by the sandwiched GO, and the arrows denote the moving direction of the GO. The times of the simulation snapshots are (from left to right) 22,160 τ, 22,240 τ, 22,480 τ, 22,800 τ, and 23,040 τ for (C) and 22,320 τ, 22,360 τ, 22,400 τ, 22,440 τ, and 22,480 τ for (D).
Intriguingly, the boundaries between regimes I and II and between regimes III and IV quantitatively coincide with two boundaries distinguishing Brownian, Lévy, and directional dynamics (Fig. 5A). In particular, in the regime without pore, the sandwiched GO diffuses via Brownian dynamics with diffusion exponent α, from the power-law fit for MSD (inset of Fig. 5B), about 1; in the regime of stable pore, the GO exhibits directional (“ballistic”) motion where α = 2. Within the broad range of regimes II and III, Lévy walk emerges, with increasing α between 1 and 2. Actually, although regime III is mathematically distinct from regime II, the metastable pore in regime III can still behave like the unstable state due to the thermal fluctuations that readily surmount the lower energy barrier. Therefore, regimes II and III are physically equivalent. Thus, such a good overlap corroborates that the transition of transport patterns can be fundamentally attributed to various membrane-pore states. In the unstable state, the formation of the pore leads to persistent walks, while the spontaneous annihilation of the pore causes intermediate jiggling, both of which combine to promote Lévy walk (Fig. 5C and movie S4). In stark contrast, the stable pore deviating from the GO center restrains the diffusion direction and favors directional motion (Fig. 5D and movie S5).
Particularly, the somewhat intractable nature of the GO material and complex biological responses makes it extremely challenging to isolate definite influences of proteins, such as biomolecular corona (45) and the proteins residing on the membrane (36), on the formation and dynamic behaviors of the sandwiched superstructures. However, we emphasize that the results conceived in the present work apply to the interaction of particles with cells under low (or absent) protein conditions, where the biological recognition is lacked but can, in itself, be very interesting for new modalities of interaction of particles with cells and thereby has an intrinsic scientific merit. Furthermore, our previous simulations have demonstrated that the sandwiched graphene–cell membrane superstructures can still occur when the fraction of the receptors is not larger than 0.1 for a tensionless membrane (29), whereas before contact with the particle, the receptor density does seem much lower (46) and a diffusive process is required for the increase of the receptor-density level (36).
Applicability of the sandwiched GO: Enhanced efficiency of membrane-specific drug delivery
To test the feasibility of membrane-specific drug delivery via the sandwiched structure, we selected tyrosine kinase inhibitors as the cargo, which could act against the transmembrane receptor (e.g., epidermal growth factor receptor), inhibit its catalytic activity, and lead to an anticancer effect (47). In comparison with the free drug vandetanib (VTB) and a classical carrier liposome (Lipo), GO significantly improves the drug cytotoxicity (Fig. 6A) and induces more death of cancer cells (Fig. 6B). Taking half-maximal inhibitory concentration as an example, the value in the GO-VTB group reduces to ~1.25 μg/ml, which is nine- and sixfold lower than that in the free VTB and Lipo-VTB group, respectively. Similar results are also obtained in different cells and different membrane receptor inhibitors (fig. S20, C and D), which are irrelevant to the empty carrier (fig. S20, A and B). Such a synergism effect could be attributed to two effects. In addition to the moderate improvement in drug entry in view of the whole cell, GO also demonstrates its excellent properties in the selective import of a greater amount of drug into the membrane owing to the unique sandwiched structure (Fig. 6C and fig. S20E). Consequently, more membrane receptors are disabled, leading to an aforementioned decrease in cell viability.
Fig. 6. The feasibility of delivering membrane-specific drugs via the sandwiched superstructure.
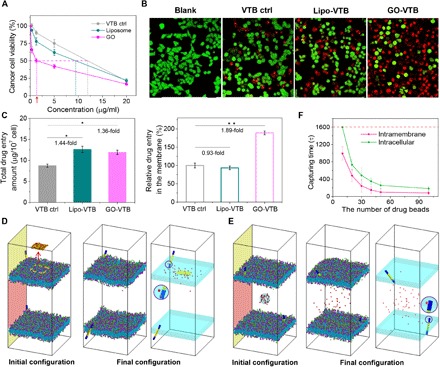
(A) Relative cell viability of VTB with the assistant of GO or liposome in breast cancer cells MCF-7. Control, ctrl. (B) Corresponding live (green)/dead (red) images at a dose of 5 μg/ml. (C) Analysis of total drug entry amount and relative drug distribution in the cell membrane. (D) The initial and final simulation configurations of the drug beads undergoing the intramembrane delivery from a sandwiched GO. Left: The GO carrying drug beads is moved away from the membrane interior for the exhibition of its initial configuration, and the dashed square marks the contour of the sandwiched GO. (E) The initial and final configurations of the drug beads undergoing the intracellular delivery. In (D) and (E), the right panel with transparent membranes displays the final configuration, where the first drug bead is captured by the transmembrane receptor, as featured by the circle. (F) The capturing time as a function of the drug-bead number for the intramembrane and intracellular deliveries.
To rationalize the experimental observations, we design a double-membrane system to simulate the membrane-specific drug deliveries from both the sandwiched GO and the intracellular region (see Materials and Methods, section S1, and fig. S6). Initially, the sandwiched GO carrying drug molecules and a cluster of drug beads are placed respectively in the membrane interior and the center of the intracellular region, with almost the same distance from the receptor (Fig. 6, D and E). Note that the sandwiched structure can still form the GO carrying drug molecules on its surface (see fig. S20F), and the drug molecules remain on the surface of the GO until it inserts into the cell membrane due to the stronger attraction between the lipid tails and the drug molecules (fig. S20G). After releasing the initial constraints for equilibrium, the drug beads diffuse along the membrane interior in the former system while they scatter within the intracellular region for the latter one (fig. S21). Here, the capturing time, defined as the period for the first drug bead to be bound by the receptor, is used to characterize the delivery efficiency, with a shorter capturing time indicating a higher efficiency (Fig. 6, D and E). As demonstrated in Fig. 6F and fig. S22, the statistics of the capturing time at different numbers of initial drug beads results in a good agreement with the experimental measurements shown in Fig. 6A, underpinning the enhanced efficiency of membrane-specific delivery for the sandwiched GO.
DISCUSSION
Here, we experimentally evidence the sandwiched graphene–cell membrane superstructure and theoretically demonstrate that the transport of such a 2D nanosheet integrated inside the cell membrane exhibits the transition of diffusion patterns from Brownian to Lévy and even directional dynamics, modulated by its interaction with the membrane interior. To gain insights into such an intriguing transition, we examine the details of the superstructures and first identify the sandwiched GO–induced pore in the leaflets of cell membranes by simulations, which is then validated by the experiments. In combination with the energetic analysis through a newly developed theoretical model, the pore is found to present unstable, metastable, and stable states. Last, a quantitative correlation between simulations and theoretical analysis corroborates that the transition of transport patterns of the sandwiched GO can be fundamentally attributable to the membrane-pore states that contribute to various directional persistence.
In light of the universal capabilities of the simulation models and the theoretical approaches, the results seem to be general for all the 2D nanomaterials. Thus, the information points toward the possible nature of the intramembrane transport of these emerging nanomaterials: the transition of transport patterns from Brownian to non-Brownian with programmable directional persistence. In principle, the findings of controllable pore states and resulting persistent transport within cell membrane have a bearing on establishing a guide for the design of novel 2D nanocarriers for precision drug delivery (e.g., targeting membrane receptors) and unique therapeutic approaches. Furthermore, such superstructures could also serve as a platform for the development of biosensors and electronic circuits where the lipid bilayer isolates the sandwiched GO from the electrically conducting physiological solutions present inside biological systems. We believe that our findings will certainly stimulate new efforts into the above promising topics of interest to materials scientists and physicists.
MATERIALS AND METHODS
GO preparation
The graphene nanosheets with a certain oxidization degree (26.1%) were prepared on the basis of previously established methods (31, 32). In particular, following extensive sonication at high power for a total time period of 8 hours in the ice, the GO solutions were ultracentrifuged at 300,000g for 4 hours (Thermo Sorvall WX 100), and the ultrasmall GOs were acquired by discarding the centrifugation sediments while preserving the supernatant. The minimum and maximum radii of the SW rotor, i.e., Rmin and Rmax, are 66.7 and 158.8 mm, respectively. The vesicle density for GO is calculated to be 1.02. The online calculator http://vesicles.niifhm.ru showed that the cutoff size is 57 nm for the maximum 300,000g after 4 hours. To concentrate the GO nanosheets, the ultrafiltration process was required, and the GO samples were diluted in ultrapure water.
Cryo-TEM was used to provide further evidence of the sandwiched graphene-membrane superstructure. Primarily, lipid bilayer vesicles were formed from a dry film of DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) via a miniextruder (100 nm of polycarbonate porous membrane). Afterward, the lipid bilayers and GO were mixed at a ratio of 5.6:1 and incubated for 2 hours at 20°C. By using a FEI Vitrobot rapid-plunging device, a 3.5-μl mixture solution was flash-frozen on a Quantifoil support foil after 3 s of blotting with filter paper. Then, the frozen-hydrated grids were transferred to liquid nitrogen before imaging. Cryo-TEM images were acquired by a FEI Talos F200C TEM (200 kV) at 36,000× magnification (with a pixel size about 0.328 nm) and under low–electron dose conditions.
Cell culture
The murine macrophage cell line J774A (phagocyte, Mφ) and the murine breast cancer cell line 4T1 (nonphagocyte, Nonφ) were supplied from the American Type Culture Collection. J774A.1 and 4T1 were cultivated in Dulbecco’s minimum essential medium and RPMI 1640 medium, respectively, at 37°C, 5% CO2. Both media were added with 10% (v/v) fetal bovine serum, penicillin (100 U/ml), and streptomycin (100 U/ml). Unless specified, GO (5 μg/ml) incubation was used in most of the cellular experiments.
Cell imaging
Cells (2 × 105/ml) were incubated with GO at 10 mg/ml for 3 hours. For confocal imaging, cells were fixed in 3.7% paraformaldehyde for 30 min, and the cell membrane was stained with a lipid probe, DiO (green). The GO-membrane interaction was initially imaged using confocal laser scanning microscopy (Leica TCS SP8) and further via HyVolution. Taking advantage of the intrinsic photoluminescence of GO in the near-infrared (NIR) region, the sample were excited at a 633-nm laser and monitored at an emission spectrum larger than a 700-nm wavelength during confocal imaging. The GO signal was marked by red.
For TEM imaging, cells were collected and fixed in 2.5% glutaraldehyde [pH 7.4, in phosphate-buffered saline (PBS)] for 1 hour at room temperature to maintain the ultrastructure of the cells as close to the living material. Following that, the samples were dehydrated through an ethanol series, passed through a propylene oxide, and then embedded in a liquid resin. Subsequently, the resin block was sectioned by a microtome (Lecia EM UC6), and the sections were collected and stained with electron-dense strains (1% lead citrate following 4% uranyl acetate) before observation. Further evidence of the GO-membrane sandwiched structure was acquired under a Hitachi H-7650B microscope.
AFM analysis
Cells were incubated with GO for 3 hours and then fixed in 3.7% paraformaldehyde in a 6-cm plastic dish. The cells with or without GO treatment were scanned by using an AFM (Bruker BioScope Catalyst) at a frequency of 1 Hz. To avoid confusing results regarding the heterogenicity on roughness and rigidity, we primarily scanned the whole cell and excluded the nucleus region via the AFM height analysis. Subsequently, the near-edge region (2.7 μm by 2.7 μm) as far from the nucleus as possible was scanned and recorded. For the roughness measurement, a plane fit was applied, and then, the statistical values (Rq) were calculated according to the heights of each pixel in the image by using NanoScope Analysis software. In addition, the 3D image was also provided with color-coded height information. To compute the Young’s modulus of cell surface, the force curves were measured, and an indentation model (Sneddon conical) was fitted to the force curves.
LDH release assay
The total release of cytoplasmic lactate dehydrogenase (LDH) into the medium is a consequence of cellular integrity damage. Cells were seeded in a 96-well plate and treated with GO for 24 hours. The cells treated with LDH release solution were defined as positive control (P-ctr), while cells without treatment were defined as negative control (N-ctr), and the medium without cells was defined as blank control. The evaluation was based on a coupled enzymatic conversion from a tetrazolium salt into a formazan product, and the absorbance was measured at 490 nm by the Infinite M200 Microplate Spectrophotometer (Tecan). All values were normalized against the P-ctr (100% LDH leakage) and the blank control (0% LDH leakage).
FRAP analysis
Cells were seeded on a petri dish overnight to encourage adhesion, and then, 2 μl of the membrane fluorescent probe DiO (initial concentration, 1000 μM) was added. After a 20-min GO incubation (10 μg/ml), cells were immediately monitored by an UltraVIEW (Perkin Elmer) under a 100× oil objective. Regions of interest in the stained membranes were noted and photobleached using a 488-nm laser operating at 13% power. Single images were then collected at maximum speed. All FRAP data were analyzed with the prepackaged analysis software, which can fit the model to experimental data reasonably through a nonlinear curve fit to f(t) = y + A ⋅ e−kt.
QCM-D testing
Before testing the GO-lipid interaction, the lipid vesicles were formed according to a standard protocol. Briefly, 10 mg of 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC; Sigma-Aldrich) was dissolved in 40 ml of chloroform. Under a nitrogen atmosphere, the lipid was dried onto the wall of a round-bottom flask by vortexing for 30 min at 25°C and then suspended in 1 ml of Milli-Q water. Lipid vesicles were formed by extruding 10 times through an 800-nm polycarbonate porous membrane (Avanti miniextruder) from the suspension to clarity. All the solvents, excluding the lipid vesicles, were sonicated before use to debubble. The first step in the actual experiment was to flush the QCM chip (Sensor Crystal QSX 301) using only Milli-Q water for at least 30 min, allowing the system to equilibrate. Subsequently, the suspension of lipid vesicles was injected, and the signal of bilayer formation was recorded. After a water rinse for removing any extra unfused vesicles, the GO suspension (20 μg/ml) was then injected in the QCM chambers. There is a linear dependence of frequency and mass change, also known as the Sauerbrey relation: .
Experimental statistical analysis
Statistical evaluations of data were performed by Student’s t test for two groups and one-way analysis of variance for multiple groups. All results were expressed as mean ± SD. *P < 0.05 was considered statistically significant. ****P < 0.0001.
Drug-loading procedure
To examine the efficacy of GO on delivering the membrane-specific drugs, the tyrosine kinase inhibitors were selected as the cargo, and classical liposome was used as a control carrier. Drugs (1 mg) were loaded on GO by using a simple adsorption method, and the loading efficiency was 73 and 74% for VTB and regorafenib (REGO), respectively. For drug-loaded liposomes, 1 mg of drug solution is primarily added to the liposome powder solvent (8 mg of DC-cholesterol and 2 mg of 1,2-distearoyl-sn-glycero-3-phosphoethanolamine (DSPE) phospholipid were dissolved in chloroform). Subsequently, liposomes (~100 nm) were prepared following a typical procedure, including lipid hydration, stirring, and downsizing.
Cell viability test for the membrane-specific drug delivery
The cytotoxicity of the loading drugs (VTB and REGO) was tested by a cell counting kit (CCK8). Typically, 5000 cancer cells (4T-1 and MCF-7) were cultured in each well (100 μl) of a 96-well plate and allowed to adhere overnight. Cells were then treated with 10-μl serial dilutions of drug or carrier-loaded drug. We also prepared wells for background absorbance measurement that contains all empty carriers except cells. After 24 hours of cell-drug incubation, 10 μl of CCK8 was added to the cells and incubated for 1 hour at 37°C. The absorbance of a water-soluble formazan product was determined on an Infinite M200 microplate spectrophotometer (Tecan) at 450 nm, which was normalized to compare with the untreated cell control. For further confirmation, cells were seeded on a petri dish, and the cell viability was detected by a LIVE/DEAD kit. On the basis of good esterase activity of live cells and impaired membrane of dead cells, live (stained by green calcein) and dead (stained by red EthD-1) cells were imaged by a confocal imaging system (Leica TCS SP5).
Drug distribution analysis of the drug-loaded cells
Cells were seeded in a 10-cm plate overnight and were exposed to different drug solutions. After cell-drug interaction for 24 hours, 107 cells were harvested and washed twice with PBS. To determine the drug distribution amount, cell membrane fractions were isolated by using a Membrane and Cytosol Extraction Kit. The drugs from different cell fractions were then extracted from the water phase (cell fraction suspensions) to the oil phase (chloroform). The amounts of drug importing into the membrane and total drug entering the cell were finally detected by using a liquid chromatography mass spectrometer (Thermo Scientific TXQ Quantum ACCESS Max) and by using a selective reaction monitoring model. To further delineate the relationship between the sandwich structure and the intracellular drug amount, the mean fluorescence intensity of cells was assayed by flow cytometry (Cytoflex), where the fluorescence was sourced from the sandwiched GO upon excitation by an 808-nm NIR laser.
Computer simulation methods
Computer simulations use the dissipative particle dynamics (DPD) technique (48), which extends the simulation scales of time and space to be appropriate to the study of nanoparticle-membrane systems with explicit water. The models of lipid, membrane, and GO are shown in fig. S6. The model of the amphiphilic lipid was constructed by a head group with three hydrophilic beads and two tails consisting of three hydrophobic beads. A total of 625 lipids self-assembled into a tensionless lipid bilayer membrane spanning the simulation box. Each GO was modeled by arranging the hydrophobic beads on a single layer of a face-centered cubic (fcc) lattice into a desired geometrical shape and size (29, 49). The modulus of the GO model was calibrated according to the experimentally found elasticity of graphene (49, 50).
In particular, the interaction parameter between GO and lipid tails, χGT, is varied to reproduce different oxidization degrees or chemical modifications of the GO. For example, increasing χGT indicates a higher oxidization degree of the GO due to the reduced attraction between GO and lipid tails. Upon interacting with the lipid bilayer membrane, the GO model leads to structures and dynamic behaviors similar to those constructed based on the typical structure model representing outcomes from standard oxidization processes (see figs. S7, S8, S14, S15, and S19, and movies S1 and S2) (29, 51, 52). Furthermore, the results based on such a model are readily generalized to other 2D nanomaterials.
The size of our simulation box is and periodic boundary condition in all directions is taken into account, where rc = 0.7 nm is the cutoff distance. To exclude the effect of system size on the diffusion of GO, we also performed simulations with a box size of . All systems were pre-equilibrated for the first 104 τ to confirm the equilibrium of the GO-sandwiched structures, while the production trajectories of the sandwiched GO are obtained from succeeding 4 × 104 τ simulations. Here, τ ≈ 7.7 ns and is the time unit used in the simulations.
In addition, to compare the efficiencies of drug delivery from a sandwiched GO and the intracellular region, we built a double-bilayer system, which divides the system into two regions: an “extracellular” region without drug bead and an “intracellular” region where the drug beads can be added into it (fig. S6). Each receptor, which will be targeted by the drug beads, is modeled as a cluster of frozen DPD beads grouped into a rigid body with fcc-arranged beads (53). Two pieces of lipid membranes have a total of 1952 lipids, with each membrane having 976 lipids. The size of such a simulation box is . The lower membrane is 10 rc away from the bottom of the box, while the upper membrane is 20 rc away from the top. Drug beads are represented by a single DPD bead.
More details on the simulation methods, models, and data analysis are given in section S1.
Development of an analytical model for the states of the sandwiched GO–induced pore
The detailed deduction can be found in section S2. Briefly, the energy cost of pore formation, ER, is determined from the governing equation
| (1) |
which originates from the balance of energies of both membrane tension and line tension of the pore. Here, R and γ are the radius and the linear tension of the pore, respectively. Am denotes the membrane area. a is the edge length of the GO. By minimizing Eq. 1, a local energy maximum at smaller R and a local energy minimum at larger R can be identified, and the transition point occurs at . When Ka > Ka0, a straightforward calculation of the minimum leads to the relation between the pore area and Ka
| (2) |
where .
Determination of the relation between GO–lipid tail interaction energy and N
The GO–lipid tail interaction energy, Ea, can be calculated as
| (3) |
In the simulations, the area of the sandwiched GO–induced pore is indicated by N, i.e., the number of GO beads that contact solvent. Thus, πR2/a2 = N/Nmax, where Nmax is the maximum of GO beads contacting solvent. After substituting this equation into Eq. 3, the interaction energy between GO and lipid tails reads
| (4) |
In DPD, Ea can be estimated through summarizing the conservative energy (54) between these two types of beads, ES. However, to eliminate the purely repulsive nature of the interaction potential adopted in DPD, ES should be amended by subtracting excess repulsion at χGT = 0, , so that the interaction energies at Ka = 0 and χGT = 0 are equal. Thus, Ea = ES − .
Supplementary Material
Acknowledgments
We thank Y. Yang, G. Zhu, and Z. Xu for stimulating discussion on the simulation results. We thank Y. Chen and B. Yuan for providing 2D samples (Xgene) and lipid vesicles, respectively. We also thank L. Zhang and S. Li for helpful suggestion and discussion on the cyro-TEM evidence. Funding: The authors acknowledge support from the National Natural Science Foundation of China (grant nos. 21873053, 51633003, 21622608, and 11504290) and the National Key R&D Program of China (grant nos. 2016YFA0202500 and 2017YFA0207900). Author contributions: H.Y., X.Z., W.W., and G.-H.M. designed and performed the experiments. H.Y., X.Z., and W.W. collected the experimental data and carried out the analysis. P.C. and L.-T.Y. contributed to the development of the computational model and to its interpretation. P.C., Z.H., and L.-T.Y. developed the analytical models and interpreted the results. L.-T.Y. and W.W. wrote the paper. All authors discussed the results and commented on the manuscript. L.-T.Y. conceived the project. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the corresponding authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/6/eaaw3192/DC1
Section S1. Details of simulation methods, models, and data analysis
Section S2. Details of analytical models
Fig. S1. Characterizations of the prepared 2D material of GO.
Fig. S2. Cryo-TEM images of the blank liposomes, the formation process of the sandwiched GO superstructure, and the sandwiched structure at different detection angles.
Fig. S3. Tomography views of the 3D map for the GO-membrane superstructure and the blank liposome vesicles.
Fig. S4. A series of TEM images of the GO–cell membrane interaction and the cells after exposure to different dimensional materials.
Fig. S5. The interaction between GO and the cells.
Fig. S6. Molecular models for the individual entities used in the simulations.
Fig. S7. Translocation pathways of GO across the lipid membrane toward the sandwiched GO structure.
Fig. S8. Translocation pathways of GO, with the model representing outcomes from standard oxidization, across the lipid membrane.
Fig. S9. The displacement probability distributions and the translational diffusion coefficients of the GO sandwiched inside the membrane.
Fig. S10. A schematic diagram illustrating the definition of the turning angle between the neighboring persistent segments.
Fig. S11. Diffusive properties of GO with χGT = 7.15.
Fig. S12. Transition of diffusion patterns of the sandwiched GO from Brownian to Lévy and even directional dynamics with a membrane size of .
Fig. S13. Diffusive dynamics and membrane-pore states of a circular GO.
Fig. S14. Simulation results demonstrate various membrane-pore states and the mechanism of pore formation.
Fig. S15. Representative snapshots from simulations feature the sandwiched GO–induced pores in the single leaflet of cell membranes.
Fig. S16. The energy of the sandwiched GO–induced pore as a function of the radius of the pore R at Ka ≥ Ka0 (Ka0 ≈ 25 kBT/nm2).
Fig. S17. Correlation between the analytical model and simulation results.
Fig. S18. Diffusive dynamics of lipids varies from Fickian to superdiffusive.
Fig. S19. Sandwiched GO–induced pores in the single leaflet of the cell membrane for the GO model representing outcomes from standard oxidization processes.
Fig. S20. The efficacy of the GO-sandwiched structure on drug delivery.
Fig. S21. Diffusive dynamics of a representative drug bead captured by the transmembrane receptor.
Fig. S22. Probability distribution of the capturing time for the drug beads released from the sandwiched GO and the center of the intracellular region.
Movie S1. Detailed translocation pathway of GO across the lipid membrane toward the sandwiched GO structure at χGT = 15.73.
Movie S2. Detailed translocation pathway of the GO model, representing outcomes from standard oxidization processes with the oxidation degree ρO = 0.3, across the lipid membrane toward the sandwiched GO structure.
Movie S3. Detailed diffusive dynamics of a sandwiched GO exhibiting Brownian motion at χGT = 1.43.
Movie S4. Detailed diffusive dynamics of a sandwiched GO exhibiting Lévy walk at χGT = 10.01.
Movie S5. Detailed diffusive dynamics of a sandwiched GO exhibiting directional motion at χGT = 14.3.
References and Notes
- 1.van Meer G., Voelker D. R., Feigenson G. W., Membrane lipids: Where they are and how they behave. Nat. Rev. Mol. Cell Biol. 9, 112–124 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Eggeling C., Ringemann C., Medda R., Schwarzmann G., Sandhoff K., Polyakova S., Belov V. N., Hein B., von Middendorff C., Schönle A., Hell S. W., Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature 457, 1159–1162 (2009). [DOI] [PubMed] [Google Scholar]
- 3.Lingwood D., Simons K., Lipid rafts as a membrane-organizing principle. Science 327, 46–50 (2010). [DOI] [PubMed] [Google Scholar]
- 4.Zhao W., Hanson L., Lou H.-Y., Akamatsu M., Chowdary P. D., Santoro F., Marks J. R., Grassart A., Drubin D. G., Cui Y., Cui B., Nanoscale manipulation of membrane curvature for probing endocytosis in live cells. Nat. Nanotechnol. 12, 750–756 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.McLaughlin S., Murray D., Plasma membrane phosphoinositide organization by protein electrostatics. Nature 438, 605–611 (2005). [DOI] [PubMed] [Google Scholar]
- 6.Anderson R. G. W., Jacobson K. A., A role for lipid shells in targeting proteins to caveolae, rafts, and other lipid domains. Science 296, 1821–1825 (2002). [DOI] [PubMed] [Google Scholar]
- 7.Wang B., Anthony S. M., Bae S. C., Granick S., Anomalous yet Brownian. Proc. Natl. Acad. Sci. U.S.A. 106, 15160–15164 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yamamoto E., Akimoto T., Kalli A. C., Yasuoka K., Sansom M. S. P., Dynamic interactions between a membrane binding protein and lipids induce fluctuating diffusivity. Sci. Adv. 3, e1601871 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Malinverno C., Corallino S., Giavazzi F., Bergert M., Li Q., Leoni M., Disanza A., Frittoli E., Oldani A., Martini E., Lendenmann T., Deflorian G., Beznoussenko G. V., Poulikakos D., Ong K. H., Uroz M., Trepat X., Parazzoli D., Maiuri P., Yu W., Ferrari A., Cerbino R., Scita G., Endocytic reawakening of motility in jammed epithelia. Nat. Mater. 16, 587–596 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Allen T. M., Cullis P. R., Drug delivery systems: Entering the mainstream. Science 303, 1818–1822 (2004). [DOI] [PubMed] [Google Scholar]
- 11.Saxena M., Liu S., Yang B., Hajal C., Changede R., Hu J., Wolfenson H., Hone J., Sheetz M. P., EGFR and HER2 activate rigidity sensing only on rigid matrices. Nat. Mater. 16, 775–781 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nel A. E., Mädler L., Velegol D., Xia T., Hoek E. M. V., Somasundaran P., Klaessig F., Castranova V., Thompson M., Understanding biophysicochemical interactions at the nano-bio interface. Nat. Mater. 8, 543–557 (2009). [DOI] [PubMed] [Google Scholar]
- 13.Pinaud F., Clarke S., Sittner A., Dahan M., Probing cellular events, one quantum dot at a time. Nat. Methods 7, 275–285 (2010). [DOI] [PubMed] [Google Scholar]
- 14.Ramadurai S., Holt A., Krasnikov V., van den Bogaart G., Killian J. A., Poolman B., Lateral diffusion of membrane proteins. J. Am. Chem. Soc. 131, 12650–12656 (2009). [DOI] [PubMed] [Google Scholar]
- 15.Saffman P. G., Delbrück M., Brownian motion in biological membranes. Proc. Natl. Acad. Sci. U.S.A. 72, 3111–3113 (1975). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen P., Huang Z., Liang J., Cui T., Zhang X., Miao B., Yan L.-T., Diffusion and directionality of charged nanoparticles on lipid bilayer membrane. ACS Nano 10, 11541–11547 (2016). [DOI] [PubMed] [Google Scholar]
- 17.Geim A. K., Graphene: Status and prospects. Science 324, 1530–1534 (2009). [DOI] [PubMed] [Google Scholar]
- 18.Geim A. K., Novoselov K. S., The rise of graphene. Nat. Mater. 6, 183–191 (2007). [DOI] [PubMed] [Google Scholar]
- 19.Kostarelos K., Novoselov K. S., Exploring the interface of graphene and biology. Science 344, 261–263 (2014). [DOI] [PubMed] [Google Scholar]
- 20.Liu Z., Robinson J. T., Tabakman S. M., Yang K., Dai H., Carbon materials for drug delivery & cancer therapy. Mater. Today 14, 316–323 (2011). [Google Scholar]
- 21.Wang Z., Zhu W., Qiu Y., Yi X., von dem Bussche A., Kane A., Gao H., Koski K., Hurt R., Biological and environmental interactions of emerging two-dimensional nanomaterials. Chem. Soc. Rev. 45, 1750–1780 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kostarelos K., Novoselov K. S., Graphene devices for life. Nat. Nanotechnol. 9, 744–745 (2014). [DOI] [PubMed] [Google Scholar]
- 23.Hong G., Diao S., Antaris A. L., Dai H., Carbon nanomaterials for biological imaging and nanomedicinal therapy. Chem. Rev. 115, 10816–10906 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Chen P., Yan L.-T., Physical principles of graphene cellular interactions: Computational and theoretical accounts. J. Mater. Chem. B 5, 4290–4306 (2017). [DOI] [PubMed] [Google Scholar]
- 25.Tu Y., Lv M., Xiu P., Huynh T., Zhang M., Castelli M., Liu Z., Huang Q., Fan C., Fang H., Zhou R., Destructive extraction of phospholipids from Escherichia coli membranes by graphene nanosheets. Nat. Nanotechnol. 8, 594–601 (2013). [DOI] [PubMed] [Google Scholar]
- 26.Li Y., Yuan H., von dem Bussche A., Creighton M., Hurt R. H., Kane A. B., Gao H., Graphene microsheets enter cells through spontaneous membrane penetration at edge asperities and corner sites. Proc. Natl. Acad. Sci. U.S.A. 110, 12295–12300 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Guo R., Mao J., Yan L.-T., Computer simulation of cell entry of graphene nanosheet. Biomaterials 34, 4296–4301 (2013). [DOI] [PubMed] [Google Scholar]
- 28.Titov A. V., Král P., Pearson R., Sandwiched graphene–membrane superstructures. ACS Nano 4, 229–234 (2010). [DOI] [PubMed] [Google Scholar]
- 29.Mao J., Chen P., Liang J., Guo R., Yan L.-T., Receptor-mediated endocytosis of two-dimensional nanomaterials undergoes flat vesiculation and occurs by revolution and self-rotation. ACS Nano 10, 1493–1502 (2016). [DOI] [PubMed] [Google Scholar]
- 30.Stone H. A., Masoud H., Mobility of membrane-trapped particles. J. Fluid Mech. 781, 494–505 (2015). [Google Scholar]
- 31.Yue H., Wei W., Yue Z., Wang B., Luo N., Gao Y., Ma D., Ma G., Su Z., The role of the lateral dimension of graphene oxide in the regulation of cellular responses. Biomaterials 33, 4013–4021 (2012). [DOI] [PubMed] [Google Scholar]
- 32.Luo N., Weber J. K., Wang S., Luan B., Yue H., Xi X., Du J., Yang Z., Wei W., Zhou R., Ma G., PEGylated graphene oxide elicits strong immunological responses despite surface passivation. Nat. Commun. 8, 14537 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Reynwar B. J., Illya G., Harmandaris V. A., Müller M. M., Kremer K., Deserno M., Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. Nature 447, 461–464 (2007). [DOI] [PubMed] [Google Scholar]
- 34.Shillcock J. C., Lipowsky R., Tension-induced fusion of bilayer membranes and vesicles. Nat. Mater. 4, 225–228 (2005). [DOI] [PubMed] [Google Scholar]
- 35.Yang K., Ma Y.-Q., Computer simulation of the translocation of nanoparticles with different shapes across a lipid bilayer. Nat. Nanotechnol. 5, 579–583 (2010). [DOI] [PubMed] [Google Scholar]
- 36.Shi X., von dem Bussche A., Hurt R. H., Kane A. B., Gao H., Cell entry of one-dimensional nanomaterials occurs by tip recognition and rotation. Nat. Nanotechnol. 6, 714–719 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Van Lehn R. C., Ricci M., Silva P. H. J., Andreozzi P., Reguera J., Voïtchovsky K., Stellacci F., Alexander-Katz A., Lipid tail protrusions mediate the insertion of nanoparticles into model cell membranes. Nat. Commun. 5, 4482 (2014). [DOI] [PubMed] [Google Scholar]
- 38.Chen K., Wang B., Guan J., Granick S., Diagnosing heterogeneous dynamics in single-molecule/particle trajectories with multiscale wavelets. ACS Nano 7, 8634–8644 (2013). [DOI] [PubMed] [Google Scholar]
- 39.Chen K., Wang B., Granick S., Memoryless self-reinforcing directionality in endosomal active transport within living cells. Nat. Mater. 14, 589–593 (2015). [DOI] [PubMed] [Google Scholar]
- 40.Edwards A. M., Phillips R. A., Watkins N. W., Freeman M. P., Murphy E. J., Afanasyev V., Buldyrev S. V., da Luz M. G. E., Raposo E. P., Stanley H. E., Viswanathan G. M., Revisiting Lévy flight search patterns of wandering albatrosses, bumblebees and deer. Nature 449, 1044–1048 (2007). [DOI] [PubMed] [Google Scholar]
- 41.M. J. Plank, M. Auger-Méthé, E. A. Codling, Lévy or not? Analyzing positional data from animal movement paths, in Dispersal, Individual Movement and Spatial Ecology: A Mathematical Perspective, M. A. Lewis, P. K. Maini, S. V. Petrovskii, Eds. (Springer, 2013). [Google Scholar]
- 42.Bennett W. F. D., Tieleman D. P., The importance of membrane defects—Lessons from simulations. Acc. Chem. Res. 47, 2244–2251 (2014). [DOI] [PubMed] [Google Scholar]
- 43.de Jager M., Weissing F. J., Herman P. M. J., Nolet B. A., van de Koppel J., Lévy walks evolve through interaction between movement and environmental complexity. Science 332, 1551–1553 (2011). [DOI] [PubMed] [Google Scholar]
- 44.Chan H., Král P., Nanoparticles self-assembly within lipid bilayers. ACS Omega 3, 10631–10637 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Castagnola V., Zhao W., Boselli L., Lo Giudice M. C., Meder F., Polo E., Paton K. R., Backes C., Coleman J. N., Dawson K. A., Biological recognition of graphene nanoflakes. Nat. Commun. 9, 1577 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gao H., Shi W., Freund L. B., Mechanics of receptor-mediated endocytosis. Proc. Natl. Acad. Sci. U.S.A. 102, 9469–9474 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zámečníkova A., Novel approaches to the development of tyrosine kinase inhibitors and their role in the fight against cancer. Expert Opin. Drug Discov. 9, 77–92 (2014). [DOI] [PubMed] [Google Scholar]
- 48.Groot R. D., Warren P. B., Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 107, 4423–4435 (1997). [Google Scholar]
- 49.Mao J., Guo R., Yan L.-T., Simulation and analysis of cellular internalization pathways and membrane perturbation for graphene nanosheets. Biomaterials 35, 6069–6077 (2014). [DOI] [PubMed] [Google Scholar]
- 50.Min S. H., Lee C., Jang J., Dissipative particle dynamics modeling of a graphene nanosheet and its self-assembly with surfactant molecules. Soft Matter 8, 8735–8742 (2012). [Google Scholar]
- 51.Lerf A., He H., Forster M., Klinowski J., Structure of graphite oxide revisited. J. Phys. Chem. B 102, 4477–4482 (1998). [Google Scholar]
- 52.Gómez-Navarro C., Meyer J. C., Sundaram R. S., Chuvilin A., Kurasch S., Burghard M., Kern K., Kaiser U., Atomic structure of reduced graphene oxide. Nano Lett. 10, 1144–1148 (2010). [DOI] [PubMed] [Google Scholar]
- 53.Yan L.-T., Popp N., Ghosh S.-K., Böker A., Self-assembly of Janus nanoparticles in diblock copolymers. ACS Nano 4, 913–920 (2010). [DOI] [PubMed] [Google Scholar]
- 54.Yamamoto S., Maruyama Y., Hyodo S.-a., Dissipative particle dynamics study of spontaneous vesicle formation of amphiphilic molecules. J. Chem. Phys. 116, 5842–5849 (2002). [Google Scholar]
- 55.Lee C., Wei X., Kysar J. W., Hone J., Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321, 385–388 (2008). [DOI] [PubMed] [Google Scholar]
- 56.Revenga M., Zúñiga I., Español P., Boundary conditions in dissipative particle dynamics. Comput. Phys. Commun. 122, 309–311 (1999). [Google Scholar]
- 57.Smith K. A., Jasnow D., Balazs A. C., Designing synthetic vesicles that engulf nanoscopic particles. J. Chem. Phys. 127, 084703 (2007). [DOI] [PubMed] [Google Scholar]
- 58.Lin J., Alexander-Katz A., Cell membranes open “doors” for cationic nanoparticles/biomolecules: Insights into uptake kinetics. ACS Nano 7, 10799–10808 (2013). [DOI] [PubMed] [Google Scholar]
- 59.Huang H. W., Chen F.-Y., Lee M.-T., Molecular mechanism of peptide-induced pores in membranes. Phys. Rev. Lett. 92, 198304 (2004). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/6/eaaw3192/DC1
Section S1. Details of simulation methods, models, and data analysis
Section S2. Details of analytical models
Fig. S1. Characterizations of the prepared 2D material of GO.
Fig. S2. Cryo-TEM images of the blank liposomes, the formation process of the sandwiched GO superstructure, and the sandwiched structure at different detection angles.
Fig. S3. Tomography views of the 3D map for the GO-membrane superstructure and the blank liposome vesicles.
Fig. S4. A series of TEM images of the GO–cell membrane interaction and the cells after exposure to different dimensional materials.
Fig. S5. The interaction between GO and the cells.
Fig. S6. Molecular models for the individual entities used in the simulations.
Fig. S7. Translocation pathways of GO across the lipid membrane toward the sandwiched GO structure.
Fig. S8. Translocation pathways of GO, with the model representing outcomes from standard oxidization, across the lipid membrane.
Fig. S9. The displacement probability distributions and the translational diffusion coefficients of the GO sandwiched inside the membrane.
Fig. S10. A schematic diagram illustrating the definition of the turning angle between the neighboring persistent segments.
Fig. S11. Diffusive properties of GO with χGT = 7.15.
Fig. S12. Transition of diffusion patterns of the sandwiched GO from Brownian to Lévy and even directional dynamics with a membrane size of .
Fig. S13. Diffusive dynamics and membrane-pore states of a circular GO.
Fig. S14. Simulation results demonstrate various membrane-pore states and the mechanism of pore formation.
Fig. S15. Representative snapshots from simulations feature the sandwiched GO–induced pores in the single leaflet of cell membranes.
Fig. S16. The energy of the sandwiched GO–induced pore as a function of the radius of the pore R at Ka ≥ Ka0 (Ka0 ≈ 25 kBT/nm2).
Fig. S17. Correlation between the analytical model and simulation results.
Fig. S18. Diffusive dynamics of lipids varies from Fickian to superdiffusive.
Fig. S19. Sandwiched GO–induced pores in the single leaflet of the cell membrane for the GO model representing outcomes from standard oxidization processes.
Fig. S20. The efficacy of the GO-sandwiched structure on drug delivery.
Fig. S21. Diffusive dynamics of a representative drug bead captured by the transmembrane receptor.
Fig. S22. Probability distribution of the capturing time for the drug beads released from the sandwiched GO and the center of the intracellular region.
Movie S1. Detailed translocation pathway of GO across the lipid membrane toward the sandwiched GO structure at χGT = 15.73.
Movie S2. Detailed translocation pathway of the GO model, representing outcomes from standard oxidization processes with the oxidation degree ρO = 0.3, across the lipid membrane toward the sandwiched GO structure.
Movie S3. Detailed diffusive dynamics of a sandwiched GO exhibiting Brownian motion at χGT = 1.43.
Movie S4. Detailed diffusive dynamics of a sandwiched GO exhibiting Lévy walk at χGT = 10.01.
Movie S5. Detailed diffusive dynamics of a sandwiched GO exhibiting directional motion at χGT = 14.3.


