Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 May 15;10(11):2957–2962. doi: 10.1021/acs.jpclett.9b00523

Orbital-Dependent Electronic Friction Significantly Affects the Description of Reactive Scattering of N2 from Ru(0001)

Paul Spiering †, Khosrow Shakouri †, Jörg Behler ‡, Geert-Jan Kroes †, Jörg Meyer †,*
PMCID: PMC6558642  PMID: 31088059

Abstract

graphic file with name jz-2019-005233_0005.jpg

Electron–hole pair (ehp) excitation is thought to substantially affect the dynamics of molecules on metal surfaces, but it is not clear whether this can be better addressed by orbital-dependent friction (ODF) or the local density friction approximation (LDFA). We investigate the effect of ehp excitation on the dissociative chemisorption of N2 on and its inelastic scattering from Ru(0001), which is the benchmark system of highly activated dissociation, with these two different models. ODF is in better agreement with the best experimental estimates for the reaction probabilities than LDFA, yields results for vibrational excitation in better agreement with experiment, but slightly overestimates the translational energy loss during scattering. N2 on Ru(0001) is thus the first system for which the ODF and LDFA approaches are shown to yield substantially different results for easily accessible experimental observables, including reaction probabilities.

In the dawning age of sustainability, chemical reactions on metal surfaces play a crucial role in heterogeneously catalyzed processes that feed and fuel our modern societies. The corresponding reaction rates are usually obtained based on the Born–Oppenheimer (BO) approximation and concomitant (adiabatic) potential energy surfaces (PESs).1,2 It has been suggested that nonadiabatic effects in the form of electron–hole pair (ehp) excitations,3−5 which are not captured within the BO approximation, may significantly affect the underlying dynamics of molecules on metal surfaces.6−12 However, nonadiabatic effects cannot be quantified by experimental data alone. Instead, state-of-the-art first-principles based computer simulations are mandatory, in combination with measurements from well-defined molecular beam experiments under clean ultrahigh vacuum conditions.

The current workhorse model for including nonadiabatic effects in simulations of molecular beam experiments is molecular dynamics with electronic friction (MDEF),13,14 with two different theoretical approaches for obtaining the electronic friction coefficients: The local density friction approximation (LDFA) determines the latter based on the surface electron density15 according to the computationally inexpensive atoms-in-jellium model.16 The LDFA enables the inclusion of all degrees of freedom of a molecule in dynamical simulations15,17 but at the same time implies the independent atom approximation (IAA) in most practical applications, thus neglecting any potential molecular effects.18,19 Obviously, this is no problem for atomic projectiles. Experiments have confirmed that the LDFA yields accurate results for hydrogen atoms scattering from metal surfaces.20,21 However, orbital-dependent friction (ODF) invokes first order time-dependent perturbation theory (TDPT) for the Kohn–Sham orbitals resulting from density functional theory calculations of an atom or molecule interacting with the surface,13,14,22−24 so that the effects of molecule’s electronic structure (i.e., no IAA) and its interaction with the surface are taken into account. ODF is thus expected to be important for reactive scattering of molecules from metal surfaces.18,25−27 However, the pragmatic use of broadening techniques for the calculation of ODF coefficients, which is currently without any alternative for calculating these coefficients on a large scale in the context of dynamical simulations,25,26,28,29 has recently been criticized to affect the values obtained for these coefficients in a way that is not well-defined within the quasi-static limit of TDPT.30 Altogether, the LDFA and ODF as formulated and implemented at present both have advantages and disadvantages. It is thus not clear a priori which model better describes dissociative chemisorption. Therefore, empirical evidence (insights based on comparisons with experimental data) is needed. Due to the very high computational cost of ODF, so far it has been used for the simulation of reactive scattering in only two systems including all six molecular degrees of freedom, i.e., H2 and D2 from Ag(111)25,28,29 and Cu(111).26 For these two system, no significant differences were found between reaction probabilities computed with ODF and the LDFA.

Given this situation, other systems are required that offer the possibility to distinguish LDFA and ODF, ideally by benchmarking against data from molecular beam experiments. For this, Luntz and co-workers have suggested N2 on Ru(0001) on the basis of extensive experimental and pioneering low-dimensional computational studies.31−33 This prototypical case of highly activated diatomic molecule dissociation has received much attention due to the relevance of N2 dissociation as rate-limiting step for ammonia production via the Haber–Bosch process.34 Recent results from LDFA calculations indicate that electronic friction is not important for the dissociative chemisorption probability,35 whereas experiments have demonstrated that N2 molecules associatively desorbing from Ru(0001) experience a large amount of vibrational quenching,36,37 which cannot be explained using BO-based theory.31,38

In this work, we show that our high-dimensional ODF model26 applied to N2 on Ru(0001), which includes frictional couplings and the motion in all six molecular degrees of freedom, reduces the dissociative chemisorption probability by about 50% compared to both adiabatic calculations and the LDFA, an effect that is almost as large as observed going from a frozen to a moving surface. Both ODF and LDFA yield good agreement for the normal translational energy loss during scattering with the corresponding experimental data, but the ODF description of concomitant vibrational excitations is better. N2 on Ru(0001) is thus the first system for which the ODF and LDFA approaches are shown to yield substantially different results for easily accessible experimental observables including reaction probabilities. The error bars on the experimental sticking probabilities still prevent an unequivocal verification of the quantitative performance of both methods. Nevertheless, our results pave the way for subsequent improved experimental studies, which can elucidate whether indeed ODF better describes the nonadiabatic reaction in this benchmark system.

We have performed MDEF13,14 calculations according to the generalized Langevin equation (GLE)

graphic file with name jz-2019-005233_m001.jpg 1

where V(rN2, rRu) is the potential energy surface that describes the (electronically adiabatic) interaction between a N2 molecule and the Ru(0001) surface consisting of mobile surface atoms described by coordinates rN2 and rRu, respectively. We have used the high-dimensional neural network (HD-NNP) PES from Shakouri et al.,39 which has been fitted to a DFT reference data set based on the RPBE functional40 using the Behler–Parinello method.41

The friction tensor ηN2 and the random forces 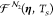Inline graphic describe the nonadiabatic coupling of the N2 molecules with electron–hole pair excitations in the surface at the surface temperature Ts. We have calculated the ODF tensor from density functional perturbation theory in the same way as in our previous work.26 This 6 × 6 tensor depends on the coordinates of the two nitrogen atoms, which are most conveniently described in the coordinate system shown in Figure 1A. Subsequently, we have constructed an accurate continuous representation using a neural network approach as detailed in the Supporting Information, which, together with the HD-NNP PES, allows calculating a large enough number of trajectories to obtain sticking probabilities that can be compared to experimental data.39,42 We neglect the influence of surface atom displacements on the friction tensor. Previous work has shown that this hardly affects the results of ab initio MDEF calculations based on the LDFA for N2 on Fe(110).43

Figure 1.

Figure 1

Open in a new tab

(A) Six-dimensional coordinate system for the description of N2 molecules on Ru(0001), consisting of the center of mass (COM) coordinates (X,Y,Z) and the N2 bond distance d as well as the polar angle θ and azimuthal angle ϕ. X,Y,Z = 0 corresponds to the position of a Ru atom in the surface plane (top site). (B) Top view of a N2 molecule with its molecular axis parallel to the surface over a bridge site in a bridge-to-hollow orientation (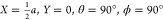Inline graphic). a denotes the surface lattice constant. First- (second-) layer Ru atoms are shown in (transparent) green. Dashed black lines show the periodic boundary conditions of a 2 × 2 super cell.

In order to numerically integrate eq 1, we have adapted a recently suggested Liouville operator technique, denoted by OVRVO in ref (44), which simplifies to the conventional velocity-Verlet algorithm45 in the absence of friction. This technique allows defining a conserved total energy,46 which has enabled us to monitor and thus ensure the accuracy of the numerical integration of the trajectories. It has also greatly simplified the analysis of the energy exchange with the surface, in particular for the nonadiabatic energy, which is dissipated into the electron–hole pair excitations in the surface.

In the following we compare results obtained with our ODF model to LDFA and adiabatic simulations for a mobile surface (BOMS) without electronic friction (i.e., without the last two terms in eq 1), focusing on a surface temperature Ts = 575 K, which is comparable to the experimental conditions for which data has been obtained31,32,47 and relevant for catalytic conditions of the Haber–Bosch cycle. In the calculations labeled ODF and LDFA, the motion of the surface atoms is also modeled. In more approximate calculations we neglect electron–hole pair excitations and also freeze all the ruthenium atoms at their equilibrium positions, resulting in the so-called Born–Oppenheimer static surface (BOSS) model, which does not allow for any energy exchange with the surface.42,48

Figure 2 shows the initial sticking probabilities for the dissociative chemisorption of N2 on Ru(0001). Except for the lowest incidence energy (1.50 eV), the BOSS model does not reproduce the experimental results.47 Including surface atom motion (BOMS) reproduces the experiment within the large systematic error bars (see Supporting Information for a discussion), as has already previously been shown.35,39 The LDFA does not yield any significant changes compared to the BOMS model. The ODF does yield significant changes, and brings the theory in better agreement with the best experimental estimates of S0. We are not aware of any other system where electronic friction has an effect on S0 with the same magnitude as surface motion. The effect of the ODF is quantified on a linear scale in the inset of Figure 2, which shows the decrease of the reaction probability of both electronic friction models relative to the BOMS results. Also on this scale, the results from the LDFA and BOMS model are hardly distinguishable. ODF, however, decreases the sticking probability, relative to BOMS, from lower to higher incidence energies by 61% to 41%.

Figure 2.

Figure 2

Open in a new tab

Reaction probability S0 as a function of the average incidence energy ⟨Ei⟩ calculated with the ODF model from this work for a surface temperature Ts = 575 K (purple diamonds). Corresponding results from Shakouri et al.35 based on the LDFA (Ts = 575 K, red triangles), the BOMS (blue triangles), and the BOSS model (green squares). Experimental data from Diekhöner et al.47 are shown for comparison (gray circles). The inset shows the ratio of reaction probabilities calculated with both electronic friction models relative to the corresponding adiabatic BOMS results.

We have also analyzed energy exchange for N2 scattering from Ru(0001) for two available experiments at different incidence energies (⟨Ei⟩). First, we compare with the translational energy loss of N2 along the surface normal (−⟨ΔE⊥⟩) in Figure 3A. At high ⟨Ei⟩, the BOMS model slightly overestimates this energy loss, while it underestimates at low ⟨Ei⟩. The effect of both ODF and LDFA is small for this observable and the same result is obtained as for BOMS for low ⟨Ei⟩, while ODF slightly overestimates at high incidence energies. In the second experiment, an upper bound of 0.05 eV has been obtained for the amount of vibrational excitation during N2 scattering from Ru(0001) at ⟨Ei⟩ = 2.8 eV. Earlier calculations within the BOSS model48 using a different RPBE-based PES42 have significantly overestimated this energy transfer ⟨ΔEvib⟩. As shown in Figure 3C, we reproduce this finding for BOSS-model-based simulations with our HD-NNP PES. Including surface mobility (BOMS) reduces the average vibrational excitation by up to 50% at the highest incidence energies, but the results are not yet compatible with the upper bound estimated from the experiments. LDFA does not yield any further improvement. Quite in contrast, ODF leads to a further reduction of 50–60% for all incidence energies, such that only this electronic friction model is compatible with the experimental upper bound.

Figure 3.

Figure 3

Open in a new tab

(A) Average translational energy loss along the surface normal −⟨ΔE⊥⟩ and (B) average change of the vibrational energy ⟨ΔEvib⟩ as a function of the average incidence energy ⟨Ei⟩ for molecules scattered from the surface. Results from adiabatic calculations according to the BOSS model (green squares), the BOMS model (blue triangles), LDFA model (red triangles), and ODF model (purple diamonds) are plotted for a surface temperature Ts = 575 K. Experimental data from Mortensen et al.32 (gray circles) are shown for comparison in (A). In (B), the maximum vibrational energy change of 0.05 eV at ⟨Ei⟩ = 2.8 eV estimated in the same study32 is indicated (gray bar). Error bars in (A) and (B) are smaller than the line size and are consequently omitted.

We attribute the big effect of ODF on S0 and vibrational excitation to the extremely large electronic friction acting along the N2 bond axis. Figures 4A–C show the corresponding friction elements ηZZ, ηdd, and ηdZ, respectively, along the minimum energy path q, at the bridge site as shown in Figure 1B, obtained by Shakouri et al.,35 and also depicted in Figure 4D, for the HD-NNP PES used in this work. The ODF tensor elements for N2 on Ru(0001) are more than five times larger than for H2 on Cu(111).26 Furthermore, as has been observed before,18,25,26,33 ODF predicts increased friction along the N2 bond compared to LDFA, i.e., 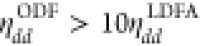Inline graphic in contrast to ηZZODF ≈ 4 ηZZ at the transition state. Moreover, the coupling between the d and Z modes is significantly smaller for LDFA compared to ODF along the reaction path that is dynamically most relevant for dissociation as discussed by Shakouri et al.39 and in our Supporting Information. Hence, it is not surprising that dynamical processes that involve N2 bond activation, like dissociation on and vibrationally inelastic scattering from the Ru(0001) surface, are accompanied by a significantly larger concomitant nonadiabatic energy loss with ODF than with LDFA. Luntz and Persson have already pointed out large differences between ODF and LDFA,18 but they did not explicitly compute sticking probabilities.33 Juaristi et al. have emphasized that modeling the motion of a N2 molecule on a metal surface in all six degrees of freedom is a crucial advantage of the LDFA15,17 over the dynamical ODF-based model in Luntz’s and Persson’s pioneering work, which only included Z and d.33 Our results for ηZZ, ηdd, and ηdZ slightly differ from theirs but still maintain the same essential features that distinguish LDFA from ODF. We show in the Supporting Information that these differences are related to a slightly different minimum energy path and the use of a different exchange-correlation functional.

Figure 4.

Figure 4

Open in a new tab

(A–C) Friction tensor elements related to the center of mass distance to the surface (ηZZ), the bond length (ηdd), and the friction-induced coupling between these two (ηdZ), respectively, along the minimum energy path q for dissociative chemisorption over the bridge site in the bridge-to-hollow orientation with the molecular axis slightly tilted off parallel from the surface (θ = 84°, see Figure 1 for the molecular coordinate system). This path is depicted in (D) together with the corresponding two-dimensional PES cut. The purple (red) lines indicate the electronic friction obtained for ODF (LDFA). Purple (red) dots show the ODF (LDFA) results from previous work of Luntz and Persson.18,33 The transition state for dissociation is located at the vertical gray line in (A–C) (q = 0 Å) and indicated by the empty circle in (D). Negative numbers up to transition state denote the approach from the gas-phase (i.e., decreasing Z above the surface). We note that in ref (33)q is defined for the strictly parallel approach of the N2 molecule toward the surface (θ = 90°), but this does not correspond to the minimum energy path in our HD-NNP PES.35

In conclusion, for N2 on Ru(0001), our ODF approach, which includes nonadiabatic coupling of the motion in all six N2 molecular degrees of freedom due to ehp excitations, yields a reduction of the dissociative chemisorption probability by about 50%. Such a large effect on a reaction probability, which is of the same order of magnitude as the inclusion of surface atom motion, has never been observed for MDEF calculations before, most of which have been based on the LDFA model. Both ODF and LDFA agree with the currently available experimental data within its sizable systematic error bars, but ODF comes closer to the best experimental estimates for S0. ODF slightly overestimates the translational energy loss during scattering, but yields results for vibrational excitation in better agreement with the aforementioned experiments than LDFA. More accurate measurements for reactive scattering of N2 from Ru(0001) would in principle allow a verdict on whether ODF or LDFA better describes the effect of ehp excitation on reaction, or whether they are equally good. We believe it is possible to measure S0 with errors no greater than a factor 1.1, using a feasible strategy that would lead to a cancellation of systematic errors (or calibration factors), as discussed in the Supporting Information.49 Likewise, absolute vibrational excitation probabilities could be measured more accurately. This might also allow to further develop theoretical modeling of nonadiabatic dynamics at metal surfaces, for example, by including higher order perturbation terms (electron-mediated phonon–phonon coupling), which Novko et al. demonstrated to play a crucial role for the nonadiabatic vibrational damping of CO on Cu(100).30,50,51 Although not suggested by our present results, improvements of the exchange-correlation functional defining the PES might be required in order to achieve quantitative agreement52,53 with the more accurate experimental data to be measured. Given the importance of N2 on Ru(0001) as a prototypical case of highly activated dissociative chemisorption, such future steps would be tremendously important to quantify how much nonadiabatic effects need to be accounted for in heterogeneous catalysis.

Computational Details

We have obtained orbital-dependent electronic friction tensors from density functional perturbation theory (DFPT)54 results based on a computational setup similar to the one we used before for H2 on Cu(111).26 Briefly, we have performed DFPT calculations as implemented in the Quantum Espresso package55 for a 2 × 2 Ru(0001) slab with five layers employing the RPBE functional40 as implemented in LibXC.56 Using ONCV57 pseudopotentials from the SG1558 library together with a plane-wave cutoff of 816 eV, a 18 × 18 × 1 k-point grid, and a Gaussian envelope technique with a width of 0.6 eV for the sum over electronic states23,30 yields converged results for the friction tensor elements. Tests with smaller widths (down to 0.15 eV) are provided in the Supporting Information. A continuous representation of the 6 × 6 frozen-surface friction tensor was obtained using neural networks constructed with the help of the TensorFlow package.59 As detailed in the Supporting Information, we base this representation on a molecular orientation that corresponds to the most significant reaction path for dissociative chemisorption. Improving our previous approach,26 special care has been taken in order to ensure positive definiteness of the friction tensor and to keep the amount of neural network weight parameters as small as possible (three hidden layers with 20 nodes each) by fitting all 21 independent friction tensor elements simultaneously.

Quasi-classical trajectory calculations with a time step of 0.3 fs were performed using the LAMMPS package,60,61 into which we have implemented our adaptation of the OVRVO algorithm.44 At every time step, we apply OVRVO by rotating to the six-dimensional coordinate system in which the ODF tensor is diagonal. The LDFA friction tensor, which is diagonal in the Cartesian representation, is the same as in ref (35), and our OVRVO implementation perfectly reproduces the results from that work. Likewise, we have taken over the equilibration procedure of the surface slab for generating initial conditions at Ts > 0 K.

Acknowledgments

This work was supported by the European Research Council through an ERC-2013 advanced grant (no. 338580) and with computer time granted by NWO-EW. J.B. is grateful for a DFG Heisenberg professorship (Be3264/11-2, project number 329898176). J.M. acknowledges financial support from the Netherlands Organisation for Scientific Research (NWO) under Vidi Grant No. 723.014.009. We thank Prof. Dr. Luntz and Dr. Montemore for scientific discussions and Prof. Dr. Auerbach for useful suggestions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.9b00523.

  • Effect of broadening width on orbital-dependent friction tensor elements, continuous representation of the orbital-dependent friction tensor, additional details on dynamical simulations, comparison with previous work, and accuracy of the measured sticking probabilities (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz9b00523_si_001.pdf (1.5MB, pdf)

References

  1. Reuter K. In Modeling Heterogeneous Catalytic Reactions: From the Molecular Process to the Technical System; Deutschmann O., Ed.; Wiley-VCH: Weinheim, 2011. [Google Scholar]
  2. Reuter K. Ab Initio Thermodynamics and First-Principles Microkinetics for Surface Catalysis. Catal. Lett. 2016, 146, 541–563. 10.1007/s10562-015-1684-3. [DOI] [Google Scholar]
  3. Lindenblatt M.; Pehlke E. Ab Initio Simulation of the Spin Transition during Chemisorption: H/Al(111). Phys. Rev. Lett. 2006, 97, 216101. 10.1103/PhysRevLett.97.216101. [DOI] [PubMed] [Google Scholar]
  4. Meyer J.; Reuter K. Electron–Hole Pairs during the Adsorption Dynamics of O2 on Pd(100): Exciting or Not?. New J. Phys. 2011, 13, 085010 10.1088/1367-2630/13/8/085010. [DOI] [Google Scholar]
  5. Rittmeyer S. P.; Meyer J.; Reuter K. Nonadiabatic Vibrational Damping of Molecular Adsorbates: Insights into Electronic Friction and the Role of Electronic Coherence. Phys. Rev. Lett. 2017, 119, 176808. 10.1103/PhysRevLett.119.176808. [DOI] [PubMed] [Google Scholar]
  6. White J. D.; Chen J.; Matsiev D.; Auerbach D. J.; Wodtke A. M. Conversion of Large-Amplitude Vibration to Electron Excitation at a Metal Surface. Nature 2005, 433, 503–505. 10.1038/nature03213. [DOI] [PubMed] [Google Scholar]
  7. Dell’Angela M.; Anniyev T.; Beye M.; Coffee R.; Fohlisch A.; Gladh J.; Katayama T.; Kaya S.; Krupin O.; LaRue J.; et al. Real-Time Observation of Surface Bond Breaking with an X-Ray Laser. Science 2013, 339, 1302–1305. 10.1126/science.1231711. [DOI] [PubMed] [Google Scholar]
  8. Ostrom H.; Oberg H.; Xin H.; LaRue J.; Beye M.; Dell’Angela M.; Gladh J.; Ng M. L.; Sellberg J. A.; Kaya S.; et al. Probing the Transition State Region in Catalytic CO Oxidation on Ru. Science 2015, 347, 978–982. 10.1126/science.1261747. [DOI] [PubMed] [Google Scholar]
  9. Diesing D.; Hasselbrink E. Chemical Energy Dissipation at Surfaces under UHV and High Pressure Conditions Studied Using Metal–Insulator–Metal and Similar Devices. Chem. Soc. Rev. 2016, 45, 3747–3755. 10.1039/C5CS00932D. [DOI] [PubMed] [Google Scholar]
  10. Wodtke A. M. Electronically Non-Adiabatic Influences in Surface Chemistry and Dynamics. Chem. Soc. Rev. 2016, 45, 3641–3657. 10.1039/C6CS00078A. [DOI] [PubMed] [Google Scholar]
  11. Montemore M. M.; Hoyt R.; Kolesov G.; Kaxiras E. Reaction-Induced Excitations and Their Effect on Surface Chemistry. ACS Catal. 2018, 8, 10358–10363. 10.1021/acscatal.8b03266. [DOI] [Google Scholar]
  12. Peña-Torres A.; Busnengo H. F.; Juaristi J. I.; Larregaray P.; Crespos C. Energy Dissipation Effects on the Adsorption Dynamics of N2 on W(100). J. Phys. Chem. C 2019, 123, 2900–2910. 10.1021/acs.jpcc.8b10173. [DOI] [Google Scholar]
  13. Hellsing B.; Persson M. Electronic Damping of Atomic and Molecular Vibrations at Metal Surfaces. Phys. Scr. 1984, 29, 360. 10.1088/0031-8949/29/4/014. [DOI] [Google Scholar]
  14. Head-Gordon M.; Tully J. C. Molecular Dynamics with Electronic Frictions. J. Chem. Phys. 1995, 103, 10137–10145. 10.1063/1.469915. [DOI] [Google Scholar]
  15. Juaristi J. I.; Alducin M.; Díez Muiño R.; Busnengo H. F.; Salin A. Role of ElectronHole Pair Excitations in the Dissociative Adsorption of Diatomic Molecules on Metal Surfaces. Phys. Rev. Lett. 2008, 100, 116102. 10.1103/PhysRevLett.100.116102. [DOI] [PubMed] [Google Scholar]
  16. Puska M. J.; Nieminen R. M. Atoms Embedded in an Electron Gas: Phase Shifts and Cross Sections. Phys. Rev. B: Condens. Matter Mater. Phys. 1983, 27, 6121. 10.1103/PhysRevB.27.6121. [DOI] [PubMed] [Google Scholar]
  17. Juaristi J. I.; Alducin M.; Muiño R. D.; Busnengo H. F.; Salin A. Juaristi et Al. Reply. Phys. Rev. Lett. 2009, 102, 109602. 10.1103/PhysRevLett.102.109602. [DOI] [Google Scholar]
  18. Luntz A. C.; Makkonen I.; Persson M.; Holloway S.; Bird D. M.; Mizielinski M. S. Comment on “Role of Electron-Hole Pair Excitations in the Dissociative Adsorption of Diatomic Molecules on Metal Surfaces. Phys. Rev. Lett. 2009, 102, 109601. 10.1103/PhysRevLett.102.109601. [DOI] [PubMed] [Google Scholar]
  19. Rittmeyer S. P.; Meyer J.; Juaristi J. I. n.; Reuter K. Electronic Friction-Based Vibrational Lifetimes of Molecular Adsorbates: Beyond the Independent-Atom Approximation. Phys. Rev. Lett. 2015, 115, 046102 10.1103/PhysRevLett.115.046102. [DOI] [PubMed] [Google Scholar]
  20. Bünermann O.; Jiang H.; Dorenkamp Y.; Kandratsenka A.; Janke S. M.; Auerbach D. J.; Wodtke A. M. Electron-Hole Pair Excitation Determines the Mechanism of Hydrogen Atom Adsorption. Science 2015, 350, 1346–1349. 10.1126/science.aad4972. [DOI] [PubMed] [Google Scholar]
  21. Kandratsenka A.; Jiang H.; Dorenkamp Y.; Janke S. M.; Kammler M.; Wodtke A. M.; Bünermann O. Unified Description of H-Atom–Induced Chemicurrents and Inelastic Scattering. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 680–684. 10.1073/pnas.1710587115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Askerka M.; Maurer R. J.; Batista V. S.; Tully J. C. Role of Tensorial Electronic Friction in Energy Transfer at Metal Surfaces. Phys. Rev. Lett. 2016, 116, 217601. 10.1103/PhysRevLett.116.217601. [DOI] [PubMed] [Google Scholar]
  23. Maurer R. J.; Askerka M.; Batista V. S.; Tully J. C. Ab Initio Tensorial Electronic Friction for Molecules on Metal Surfaces: Nonadiabatic Vibrational Relaxation. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 115432. 10.1103/PhysRevB.94.115432. [DOI] [Google Scholar]
  24. Askerka M.; Maurer R. J.; Batista V. S.; Tully J. C. Erratum: Role of Tensorial Electronic Friction in Energy Transfer at Metal Surfaces [Phys. Rev. Lett. 116, 217601 (2016)]. Phys. Rev. Lett. 2017, 119, 069901 10.1103/PhysRevLett.119.069901. [DOI] [PubMed] [Google Scholar]
  25. Maurer R. J.; Jiang B.; Guo H.; Tully J. C. Mode Specific Electronic Friction in Dissociative Chemisorption on Metal Surfaces: H2 on Ag(111). Phys. Rev. Lett. 2017, 118, 256001. 10.1103/PhysRevLett.118.256001. [DOI] [PubMed] [Google Scholar]
  26. Spiering P.; Meyer J. Testing Electronic Friction Models: Vibrational De-Excitation in Scattering of H2 and D2 from Cu(111). J. Phys. Chem. Lett. 2018, 9, 1803–1808. 10.1021/acs.jpclett.7b03182. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lončarić I.; Alducin M.; Juaristi J. I.; Novko D. CO Stretch Vibration Lives Long on Au(111). J. Phys. Chem. Lett. 2019, 10, 1043–1047. 10.1021/acs.jpclett.9b00069. [DOI] [PubMed] [Google Scholar]
  28. Maurer R. J.; Zhang Y.; Guo H.; Jiang B. Hot Electron Effects during Reactive Scattering of H2 from Ag(111): Assessing the Sensitivity to Initial Conditions, Coupling Magnitude, and Electronic Temperature. Faraday Discuss. 2019, 10.1039/C8FD00140E. [DOI] [PubMed] [Google Scholar]
  29. Zhang Y.; Maurer R.; Guo H.; Jiang B. Hot-Electron Effects during Reactive Scattering of H2 from Ag(111): The Interplay between Mode-Specific Electronic Friction and the Potential Energy Landscape. Chem. Sci. 2019, 10, 1089–1097. 10.1039/C8SC03955K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Novko D.; Alducin M.; Blanco-Rey M.; Juaristi J. I. Effects of Electronic Relaxation Processes on Vibrational Linewidths of Adsorbates on Surfaces: The Case of CO/Cu(100). Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 224306. 10.1103/PhysRevB.94.224306. [DOI] [Google Scholar]
  31. Diekhöner L.; Hornekær L.; Mortensen H.; Jensen E.; Baurichter A.; Petrunin V. V.; Luntz A. C. Indirect Evidence for Strong Nonadiabatic Coupling in N2 Associative Desorption from and Dissociative Adsorption on Ru(0001). J. Chem. Phys. 2002, 117, 5018–5030. 10.1063/1.1498476. [DOI] [Google Scholar]
  32. Mortensen H.; Jensen E.; Diekhöner L.; Baurichter A.; Luntz A. C.; Petrunin V. V. State Resolved Inelastic Scattering of N2 from Ru(0001). J. Chem. Phys. 2003, 118, 11200–11209. 10.1063/1.1575210. [DOI] [Google Scholar]
  33. Luntz A. C.; Persson M. How Adiabatic Is Activated Adsorption/Associative Desorption?. J. Chem. Phys. 2005, 123, 074704 10.1063/1.2000249. [DOI] [PubMed] [Google Scholar]
  34. Honkala K.; Hellman A.; Remediakis I. N.; Logadottir A.; Carlsson A.; Dahl S.; Christensen C. H.; Nørskov J. K. Ammonia Synthesis from First-Principles Calculations. Science 2005, 307, 555–558. 10.1126/science.1106435. [DOI] [PubMed] [Google Scholar]
  35. Shakouri K.; Behler J.; Meyer J.; Kroes G.-J. Analysis of Energy Dissipation Channels in a Benchmark System of Activated Dissociation: N2 on Ru(0001). J. Phys. Chem. C 2018, 122, 23470–23480. 10.1021/acs.jpcc.8b06729. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Murphy M. J.; Skelly J. F.; Hodgson A.; Hammer B. Inverted Vibrational Distributions from N2 Recombination at Ru(001): Evidence for a Metastable Molecular Chemisorption Well. J. Chem. Phys. 1999, 110, 6954–6962. 10.1063/1.478601. [DOI] [Google Scholar]
  37. Diekhöner L.; Mortensen H.; Baurichter A.; Luntz A. C. Laser Assisted Associative Desorption of N2 and CO from Ru(0001). J. Chem. Phys. 2001, 115, 3356–3373. 10.1063/1.1386810. [DOI] [PubMed] [Google Scholar]
  38. Dìaz C.; Perrier A.; Kroes G. J. Associative Desorption of N2 from Ru(0001): A Computational Study. Chem. Phys. Lett. 2007, 434, 231–236. 10.1016/j.cplett.2006.12.016. [DOI] [Google Scholar]
  39. Shakouri K.; Behler J.; Meyer J.; Kroes G.-J. Accurate Neural Network Description of Surface Phonons in Reactive Gas–Surface Dynamics: N 2 + Ru(0001). J. Phys. Chem. Lett. 2017, 8, 2131–2136. 10.1021/acs.jpclett.7b00784. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Hammer B.; Hansen L. B.; Norskov J. K. Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 7413–7421. 10.1103/PhysRevB.59.7413. [DOI] [Google Scholar]
  41. Behler J.; Parrinello M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98, 146401. 10.1103/PhysRevLett.98.146401. [DOI] [PubMed] [Google Scholar]
  42. Díaz C.; Vincent J. K.; Krishnamohan G. P.; Olsen R. A.; Kroes G. J.; Honkala K.; Norskov J. K. Multidimensional Effects on Dissociation of N2 on Ru(0001). Phys. Rev. Lett. 2006, 96, 096102 10.1103/PhysRevLett.96.096102. [DOI] [PubMed] [Google Scholar]
  43. Novko D.; Blanco-Rey M.; Alducin M.; Juaristi J. I. Surface Electron Density Models for Accurate Ab Initio Molecular Dynamics with Electronic Friction. Phys. Rev. B 2016, 93, 245435. 10.1103/PhysRevB.93.245435. [DOI] [Google Scholar]
  44. Sivak D. A.; Chodera J. D.; Crooks G. E. Time Step Rescaling Recovers ContinuousTime Dynamical Properties for Discrete-Time Langevin Integration of Nonequilibrium Systems. J. Phys. Chem. B 2014, 118, 6466–6474. 10.1021/jp411770f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Verlet L. Computer ”Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98. 10.1103/PhysRev.159.98. [DOI] [Google Scholar]
  46. Bussi G.; Donadio D.; Parrinello M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
  47. Diekhöner L.; Mortensen H.; Baurichter A.; Jensen E.; Petrunin V. V.; Luntz A. C. N2 Dissociative Adsorption on Ru(0001): The Role of Energy Loss. J. Chem. Phys. 2001, 115, 9028–9035. 10.1063/1.1413746. [DOI] [Google Scholar]
  48. Díaz C.; Vincent J. K.; Krishnamohan G. P.; Olsen R. A.; Kroes G. J.; Honkala K.; Nørskov J. K. Reactive and Nonreactive Scattering of N2 from Ru(0001): A SixDimensional Adiabatic Study. J. Chem. Phys. 2006, 125, 114706. 10.1063/1.2229197. [DOI] [PubMed] [Google Scholar]
  49. Auerbach D. J. Methods to get accurate measurements of small molecular adsorption probabilities. Private communication, 2019. [Google Scholar]
  50. Novko D.; Alducin M.; Juaristi J. I. Electron-Mediated Phonon-Phonon Coupling Drives the Vibrational Relaxation of CO on Cu(100). Phys. Rev. Lett. 2018, 120, 156804. 10.1103/PhysRevLett.120.156804. [DOI] [PubMed] [Google Scholar]
  51. Novko D.; Tremblay J. C.; Alducin M.; Juaristi J. I. Ultrafast Transient Dynamics of Adsorbates on Surfaces Deciphered: The Case of CO on Cu(100). Phys. Rev. Lett. 2019, 122, 016806 10.1103/PhysRevLett.122.016806. [DOI] [PubMed] [Google Scholar]
  52. Diaz C.; Pijper E.; Olsen R. A.; Busnengo H. F.; Auerbach D. J.; Kroes G. J. Chemically Accurate Simulation of a Prototypical Surface Reaction: H2 Dissociation on Cu(111). Science 2009, 326, 832–834. 10.1126/science.1178722. [DOI] [PubMed] [Google Scholar]
  53. Nattino F.; Migliorini D.; Kroes G.-J.; Dombrowski E.; High E. A.; Killelea D. R.; Utz A. L. Chemically Accurate Simulation of a Polyatomic Molecule-Metal Surface Reaction. J. Phys. Chem. Lett. 2016, 7, 2402–2406. 10.1021/acs.jpclett.6b01022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Baroni S.; de Gironcoli S.; Corso A. D.; Giannozzi P. Phonons and Related Crystal Properties from Density-Functional Perturbation Theory. Rev. Mod. Phys. 2001, 73, 515–562. 10.1103/RevModPhys.73.515. [DOI] [Google Scholar]
  55. Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; et al. QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys.: Condens. Matter 2009, 21, 395502. 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  56. Marques M. A. L.; Oliveira M. J. T.; Burnus T. Libxc: A Library of Exchange and Correlation Functionals for Density Functional Theory. Comput. Phys. Commun. 2012, 183, 2272–2281. 10.1016/j.cpc.2012.05.007. [DOI] [Google Scholar]
  57. Hamann D. R. Optimized Norm-Conserving Vanderbilt Pseudopotentials. Phys. Rev. B 2013, 88, 085117. 10.1103/PhysRevB.88.085117. [DOI] [Google Scholar]
  58. Schlipf M.; Gygi F. Optimization Algorithm for the Generation of ONCV Pseudopotentials. Comput. Phys. Commun. 2015, 196, 36–44. 10.1016/j.cpc.2015.05.011. [DOI] [Google Scholar]
  59. a Abadi M.; Agarwal A.; Barham P.; Brevdo E.; Chen Z.; Citro C.; Corrado G. S.; Davis A.; Dean J.; Devin M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv:1603.04467 [cs], 2016. Software available from tensorflow.org.; b Abadi M.; Barham P.; Chen J.; Chen Z.; Davis A.; Dean J.; Devin M.; Ghemawat S.; Irving G.; Isard M.; et al. TensorFlow: A System for LargeScale Machine Learning. Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI ′16). Savannah, GA, USA, 2016; pp 265–283.
  60. Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  61. Singraber A.; Behler J.; Dellago C. Library-Based LAMMPS Implementation of High-Dimensional Neural Network Potentials. J. Chem. Theory Comput. 2019, 15, 1827–1840. 10.1021/acs.jctc.8b00770. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz9b00523_si_001.pdf (1.5MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES