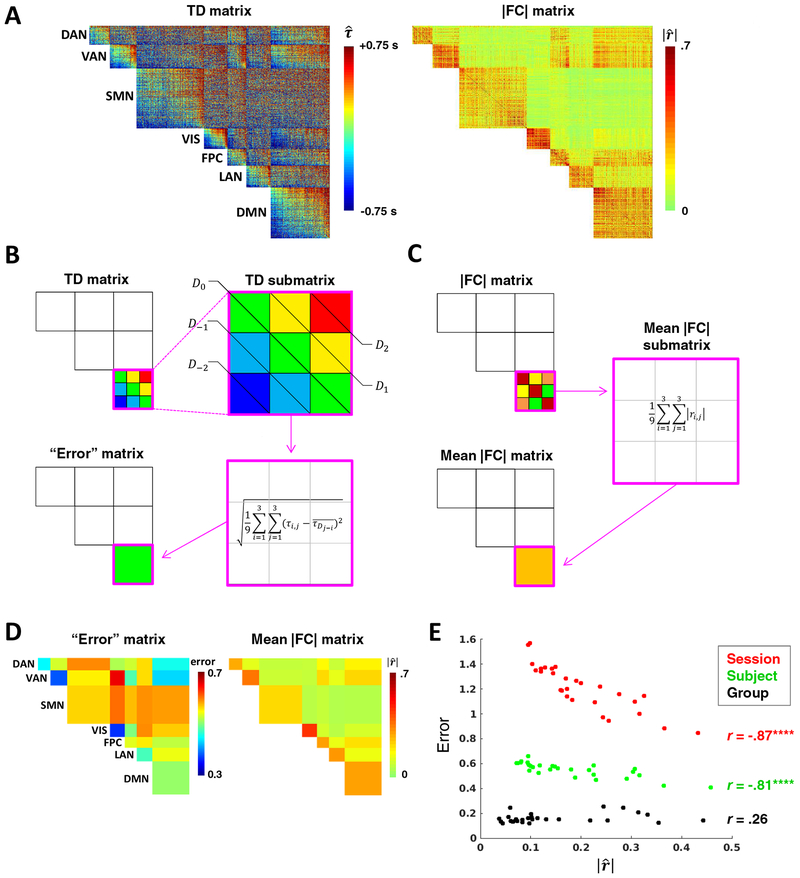
Figure 5. Temporal structure in intra- and inter-network relationships is obscured by sampling error.
(A) Subject-level (MSC01) TD (left) and |FC| (right) matrices comprising 6 mm gray matter cube ROIs grouped by functional network (as in Fig. 1D). (B) Toy case illustrating computation of blockwise diagonal “error” (non-square blocks are first interpolated to yield square blocks). TD matrix blocks in (A) that appear more organized seem to comprise (roughly) iso-latent diagonals. Thus, temporal structure of a given block (submatrix) can be estimated as the RMSE of all time delays in the block relative to the mean delay of their respective diagonals. Error of the perfectly structured toy submatrix amounts to 0. Repeating this process for each unique block yields an error matrix. (C) Toy case illustrating computation of the mean |FC| matrix. (D) MSC01 error and mean |fC| matrices computed from the TD and |FC| matrices shown in (a). Submatrices were interpolated to be square before computing diagonals. (The main diagonal is all zeroes by definition and therefore excluded in error computations). (E) Error in temporal structure as a function of mean |FC|, computed for the 28 unique network blocks at the session (MSC01 session 1), subject (MSC01) and group (MSC average) levels. Error is strongly inversely correlated with FC magnitude at the session and subject levels. At the group level (3,000 minutes of data), this correlation is not significant. Note overall decrease in error and leftward shift of values associated with increasing data. (****p <.0001; N = 28 blocks). DAN, dorsal attention network; VAN, ventral attention network; SMN, sensorimotor network; VIS, visual network; FPC, frontoparietal control network; LAN, language network; DMN, default mode network.