Figure 2. Periodic output task.

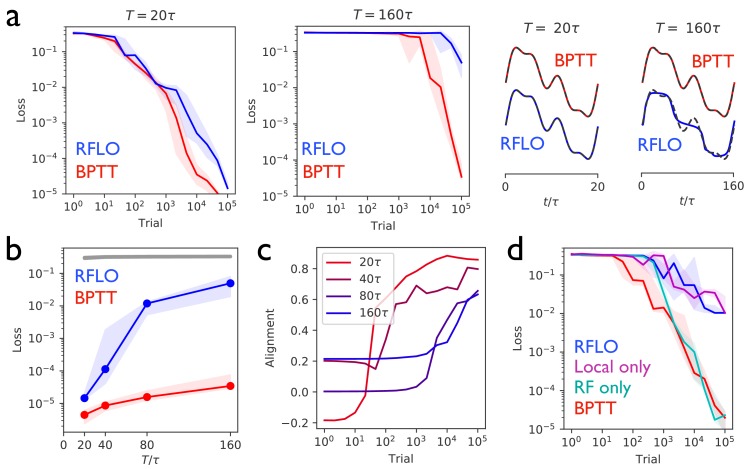
(a) Left panels: The mean squared output error during training for an RNN with $N=30$ recurrent units and no external input, trained to produce a one-dimensional periodic output with period of duration $T=20\tau$ (left) or $T=160\tau$ (right), where $\tau =10$ is the RNN time constant. The learning rules used for training were backpropagation through time (BPTT) and random feedback local online (RFLO) learning. Solid line is median loss over nine realizations, and shaded regions show 25/75 percentiles. Right panels: The RNN output at the end of training for each type of learning (dashed lines are target outputs, offset for clarity). (b) The loss function at the end of training for target outputs having different periods. The colored lines correspond to the two learning rules from (a), while the gray line is the loss computed for an untrained RNN. (c) The normalized alignment between the vector of readout weights ${\mathbf{𝐖}}^{\mathrm{out}}$ and the vector of feedback weights $\mathbf{𝐁}$ during training with RFLO learning. (d) The loss function during training with $T=80\tau$ for BPTT and RFLO, as well as versions of RFLO in which locality is enforced without random feedback (magenta) or random feedback is used without enforcing locality (cyan).

Figure 2—figure supplement 1. An RNN with sign-constrained synapses comporting with Dale’s law attains performance similar to an unconstrained RNN.

(a) In the periodic output task from Figure 2, the loss function during training with RFLO learning shows similar rate of decrease in an RNN with sign-constrained synapses (RFLO + Dale) compared with an RNN trained without sign constraint (RFLO), both for short-duration (left) and long-duration (right) outputs. (b) The final loss function value after training is similar for RNNs with and without sign-constrained synapses for outputs of various durations.

Figure 2—figure supplement 2. An RNN trained to perform the task from Figure 2 with RFLO learning on recurrent and readout weights outperforms an RNN in which only readout weights or only recurrent weights are trained.

Figure 2—figure supplement 3. The performance of an RNN trained to perform the task from Figure 2 with RFLO learning improves with larger network sizes and larger initial recurrent weights.

(a) The loss after 10⁴ trials in RNNs versus the number of recurrent units. (b) The loss after 10⁴ trials in RNNs versus the standard deviation of the initial weights. In these RNNs, the recurrent weights were initialized as $W_{ij}\sim 𝒩(0,g^2/N)$, and the readout weights were initialized as $W_{ij}^{\mathrm{out}}\sim 𝒰(-1,1)g/\sqrt{N}$, where $𝒰(-1,1)$ is the uniform distribution over (−1,1).