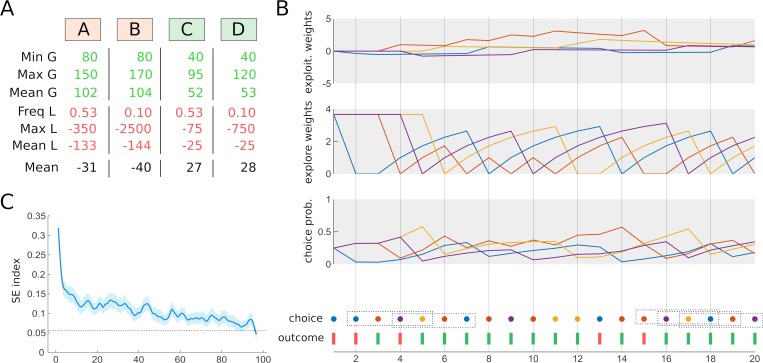
Fig 1. Directed exploration in the IOWA Gambling Task.

(A) In the IGT, participants must sample 4 decks of card associated with gains and losses whose magnitudes vary in a probabilistic manner. Unbeknownst to participants, decks C and D are advantageous despite offering smaller gains, because the losses are respectively very low or rarely encountered. The columns below each deck report the empirical minimum, maximum and average magnitude of gains (all decks have a 100% gain probability), the frequency, maximum and mean magnitude of losses, as well as the overall expected value. (B) Here, we propose a new computational model accounting for trial-by-trial choices in the IGT. The “Value and Sequential Exploration” (VSE) model consist of two learning modules tracking respectively the net amount of money generated (exploitation weights, top) and the exploration weights of each deck (dependent upon the time elapsed since the last selection of that deck). These two weights are then summed and transformed into a probability of choosing each deck through a classical softmax. As such, the model implements a straightforward arbitration between reward- and information-seeking drives. (C) The VSE architecture was justified by the discovery of a peculiar choice pattern in the IGT, that it can reproduce for some combination of parameters. Namely, the probability of choosing 4 different decks within 4 consecutive trials (a pattern referred to as the SE index) was largely above chance levels, especially in the beginning of the task.