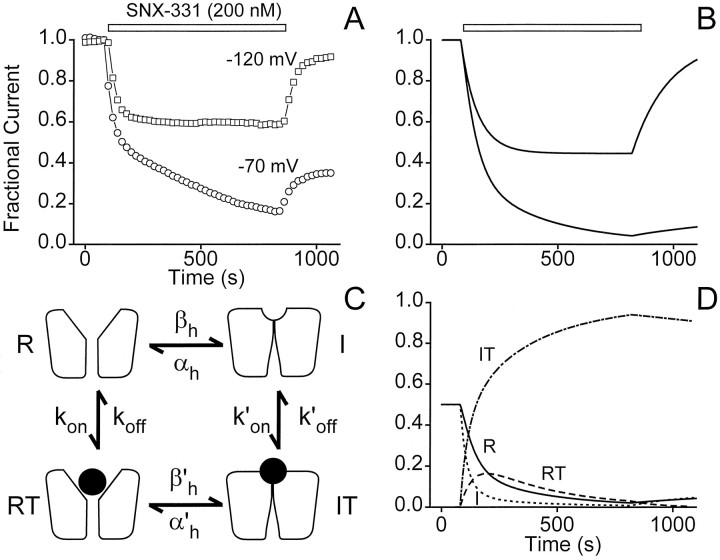
Fig. 7.

Simulation of voltage-dependent block by a modulated receptor scheme. An attempt to model the voltage dependence of block (A) using the modulated receptor scheme diagrammed in C yielded the results shown inB. The data in A showing the voltage dependence of toxin-blocking characteristics are identical to that shown in Figure 1A. Good agreement is observed between a comparison of data (A) with the predictions made by the model (B). The modulated receptor scheme used to generate the predicted blocking behavior includes four states of the channel; resting (R), inactivated (I), resting with toxin bound (RT), and inactivated with toxin bound (IT). Appropriate differential equations were solved numerically with Matlab (fourth and fifth order Runge–Kutta formulas for integration). The parameters shown inC were given the following values:k_on = 4 × 10⁴m⁻¹ · sec⁻¹,k_off = 8 × 10⁻³sec⁻¹, k′_on = 1.6 × 10⁵m⁻¹ · sec⁻¹,k′_off = 1.368 × 10⁻⁴sec⁻¹, β_h(−70 mV) = α_h(−70 mV) = 0.01 sec⁻¹, β_h(−120 mV) = 2 × 10⁻⁴ sec⁻¹, α_h(−120 mV) = 0.2 sec⁻¹, β′_h(−70 mV) = 4 × 10⁻⁴ sec⁻¹, α′_h(−70 mV) = 1.71 × 10⁻⁶sec⁻¹, β′_h(−120 mV) = 8 × 10⁻³ sec⁻¹, and α′_h(−120 mV) = 3.42 × 10⁻² sec⁻¹. The fractional populations of the four states of the model are plotted separately inD for the case in which toxin is applied and washed out at the depolarized potential of −70 mV. The rapid buildup of a large population of channels in the inactivated toxin-bound state (IT) during application of toxin can be easily seen.