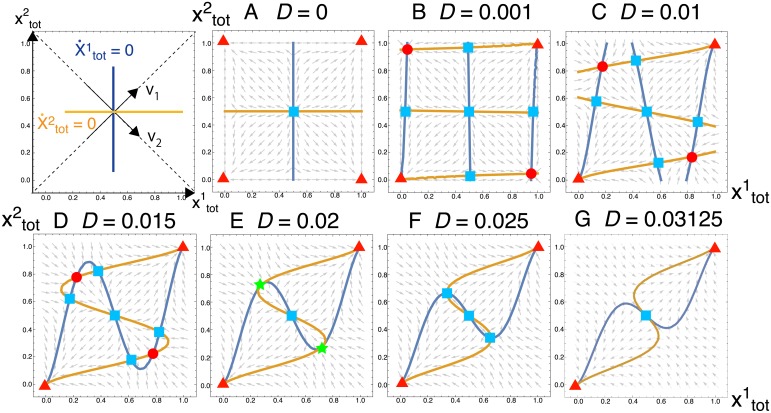
Fig 5. Flow diagram of Eq (10).

As schematically indicated in the left-top panel, the nullclines are shown for ${\dot{x}}_{tot}^1=0$ and ${\dot{x}}_{tot}^2=0$ in blue and orange, respectively, and the crossing points of them are solutions. The directions of v₁ = (1, 1) and v₂ = (1, −1) are also indicated. For the solutions, stable fixed points are shown in red: those with stable growth [i.e., both fragments are in each subsystem] are in red circles, and those without growth [either of fragments is lost from subsystems or whole systems] are in red triangles. Unstable solutions are in light-blue squares, and neutral solutions in the v₁-direction are in green stars at D = 0.02 (E). For D = 0 (A), the solution exists at $(x_{tot}^1,x_{tot}^2)=(1/2,1/2)$ but it is unstable. For small values of D (B to D), the stable fixed points with growth [red circles] appear in addition to fixed points without growth. At D = 0.02 (E), the fixed points with growth get unstable [shown in green stars] in v₁-directions. As D increases further (F), the two fixed points are still stable in v₂-directions, while the solution at $(x_{tot}^1,x_{tot}^2)=(1/2,1/2)$ is unstable in the direction. At D = 0.03125 (G), the system transits from the three fixed points to one fixed point.