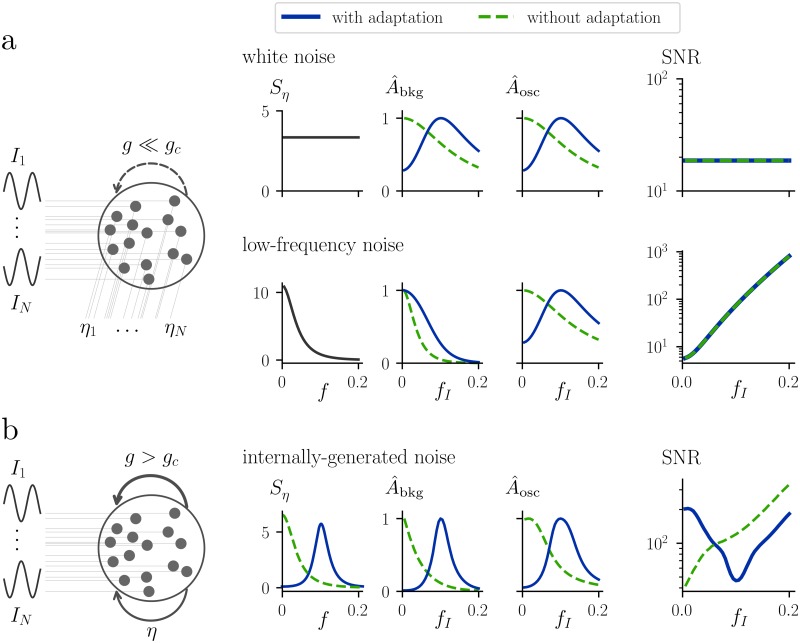
Fig 5. Adaptation shapes the SNR in the chaotic regime.

a: For small g, a recurrent network driven by an oscillatory input and external noise can be analyzed in the linear response theory framework. Top row: response of the network to oscillatory drive and independent white noise to each neuron. Bottom row: response of the network to oscillatory drive and independent low-frequency noise to each neuron. For each row, from left to right, we plot the power spectrum of the input noise, the background component of the power spectrum ${\widehat{A}}_{\text{osc}}$, the oscillatory component of the power spectrum ${\widehat{A}}_{\text{osc}}$, and the SNR as a function of the driving frequency. The hat over the symbols A_bkg and A_osc indicates that, to highlight the network shaping, they are normalized to have the same maximum height (equal to one). Notice that, since both signal and noise are shaped in the same way in the linear response framework, the introduction of adaptation does not affect the SNR. b: For large g, the network is subject to internally generated noise and driven by oscillatory input. We plot the same quantities as in panel a. Notice that, due to the nonlinearity of the network, signal and internally-generated noise are shaped in different ways, with the signal being subject to a broader effective filter. As a consequence, the introduction of adaptation in the nonlinear network shapes the SNR by favoring low frequencies. Parameters of the network with adaptation for all panels: γ = 0.25, β = 1 g = 2g_c(γ, β) and A_I = 0.5.