Fig. 1. Quantum adiabaticity of continuous driving.

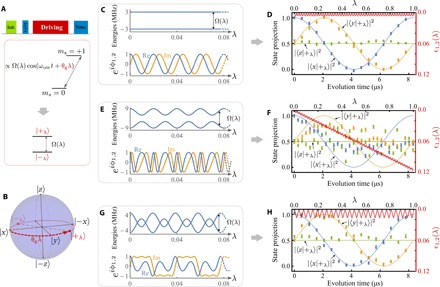
(A) Illustration of experimental control. An MW resonant with an NV transition forms in the rotating frame a Hamiltonian with the instantaneous eigenstates ∣ψ₁(λ)〉 = ∣+_λ〉 and ∣ψ₂(λ)〉 = ∣−_λ〉 that are separated by an energy gap Ω(λ) proportional to the amplitude of the MW field. (B) Evolving path (red curve with an arrowhead) on the Bloch sphere when increasing the parameter λ = λ(t) in the MW phase with the evolution time t. (C) The energies of the eigenstates for a constant gap Ω(λ) = Ω₀ = 2π × 6 MHz and the corresponding real (Re) and imaginary (Im) parts of e^iϕ_1,2 as a function of λ. (D) The measured projections (dots) of the system state on the ∣x〉, ∣y〉, and ∣z〉 states. The system state was initialized in ∣+_{λ = 0}〉 = ∣x〉 [see (B)] and subsequently driven by the Hamiltonian with the eigenenergies shown in (C) and with a changing rate dλ/dt = 0.12 MHz and a path length θ_g = 2π. The lines show the ideal state projections of the instantaneous eigenstate ∣+_λ〉. The red line is a plot of ϵ_1,2(λ), i.e., the interference of e^iϕ_1,2 at different path points. (E and F) Same as (C) and (D), respectively, but for a gap Ω(λ) = Ω₀[2 + cos (Ω₀λT)], larger than the gap in (C). Because ε_1,2(λ) is not negligible, the corresponding evolution in (F) is not adiabatic. (G and H) Same as (C) and (D), respectively, but for the gap Ω(λ) = Ω_π(λ) that has energy level crossings. ϵ_1,2(λ) is negligible and induces the quantum adiabatic evolution shown in (H). The error bars in all the figures represent two SEM.