Fig. 2. Recovery of quantum adiabaticity by adding energy gap fluctuations.

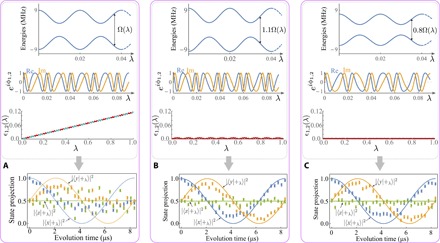
(A) The energies of instantaneous eigenstates, the real and imaginary parts of e^iϕ_1,2, ϵ_1,2(λ), and the measured projections (dots) of the system state on the ∣x〉, ∣y〉, or ∣z〉 states. The results are the same as those in Fig. 1 (E and F) where the energy gap Ω(λ) = Ω₀[2 + cos (Ω₀λT)]. (B and C) Same as (A) but changing the energy gap to Ω(λ) → 1.1Ω(λ) and Ω(λ) → 0.8Ω(λ), respectively, by adding an amplitude bias in the control field of the experiments. The fluctuation in the energy gap induces random modulation on the function e^iϕ_1,2. The destructive interference on e^iϕ_1,2 leads to a smaller average ϵ_1,2(λ) and hence improved quantum adiabatic evolution. In (A), the cyan dashed line in the plot of ϵ_n,m(λ) shows the line J₂(1)λ ≈ 0.115λ.