Fig. 3. Transition of adiabatic driving from the standard continuous protocol to the jumping protocol.

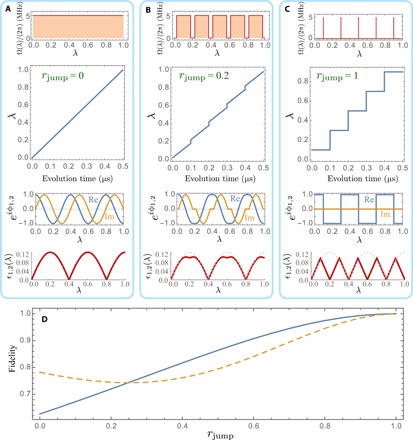
(A) Relations among the energy gap Ω(λ), path parameter λ, evolution time t, phase factor e^iϕ_1,2(λ), and ϵ_1,2(λ) for the standard adiabatic driving with a constant gap Ω₀ = 2π × 5 MHz. (B and C) Same as (A) with the maximum gap Ω₀ = 2π × 5 MHz but with a ratio r_jump of intervals to have Ω(λ) = 0 along the path parameter λ. Therefore, the case of r_jump = 0 corresponds to the standard adiabatic protocol without a vanishing gap. A ratio r_jump > 0 in (B) opens regions that have Ω(λ) = 0. For the maximum value r_jump = 1, we get in (C) the jumping protocol that only drives the system at discrete path points with a Rabi frequency equalling Ω₀. For comparison, the plot of ϵ_1,2(λ) in (A) is also shown in (B) and (C) by a gray dashed line. (D) Calculated fidelity to the ideal adiabatic state at the final time as a function of r_jump. The fidelity increases to 100% when the driving is getting to the jumping protocol. The solid line shows the case that the initial state is prepared in the initial eigenstate ∣x〉 of the Hamiltonian, while the dashed line is the result for the initial state being the superposition state ∣y〉. The driving is along the adiabatic path given in Eq. 5 with θ_g = π and is repeated back and forth three times for a total time T = 3 μs.