NMR relaxation and magnetic properties of superparamagnetic nanoworms

Abstract

Maghemite particles are used as T₂ contrast agents for magnetic resonance imaging, especially for molecular and cellular imaging. Linear clusters of particles – called nanoworms – were recently developed to enhance the targeting efficiency. In this work, the magnetic and NMR relaxation properties of these nanoworms are studied at multiple magnetic fields. After the usual saturation at 0.5 T, the magnetization of the worms is still increasing, which results in an appreciable increase of the transverse relaxivity at high magnetic fields. The obtained relaxivities are typical of superparamagnetic particles of iron oxide (SPIOs). The transverse relaxation of the worms is clearly more efficient than for the isolated grains, which is confirmed by computer simulations. At high field, the longitudinal relaxation of the worms is less pronounced than for the grains, as expected for SPIOs. The nanoworms thus constitute a promising T₂ agent for cellular and molecular imaging.

1. Introduction

Superparamagnetic particles have been used for many years as contrast agents for magnetic resonance imaging (MRI) (1–3). They are composed of maghemite nanoparticles coated by different molecules (dextran, PEG, etc.). These particles considerably shorten the transverse relaxation time of water protons, which causes a darkening of T₂-weighted MR images. Two kinds of iron oxide particles can be differentiated: superparamagnetic particles of iron oxide (SPIOs) and ultrasmall particles of iron oxide (USPIOs). SPIOs contain several maghemite crystals within the same permeable coating. Their hydrodynamic diameter is often larger than 40 nm. Standard SPIOs are injected intravenously. However, some of them, intended for gastro-intestinal imaging, are administered orally. On the other hand, USPIOs (also called MIONs, monocrystalline iron oxide nanoparticles) contain a single maghemite crystal and their hydrodynamic diameter is smaller than 40 nm. This type of agent is always injected intravenously

The efficiency of a contrast agent is given by the longitudinal (r₁) and transverse (r₂) relaxivities. Maghemite particles exhibit very large r₂ values, which make them excellent agents for molecular and cellular imaging. Indeed, the higher the relaxivities, the smaller the quantity of product to be brought to a specific target in the body. The magnetic and relaxometric properties of SPIOs and USPIOs have been intensively studied in the past (4–7). SPIO typically present larger transverse relaxivities than USPIOs, but their longitudinal relaxivity at high magnetic fields is lower. Interestingly, Bulte et al. (5) also showed that a fraction of the iron ions in such iron oxide nanoparticles could be in the paramagnetic state. This fraction was evaluated at 41% for MION-46L, causing a linear increase of the sample magnetization after the saturation of the superparamagnetic moments which occurs at 0.25 T. They also used two different size populations of superparamagnetic particles to fit their magnetometric data.

Different groups have proposed using clustered particles (similar to SPIOs) for molecular imaging, since the transverse relaxivity of such systems is superior (8,9). Recently, an elongated assembly of maghemite particles (called nanoworm) was developed using high-molecular-weight dextran, in order to increase the targeting efficiency (10). The structure is composed of a chain of five to 10 magnetic grains each of 5 nm diameter, possessing a global hydrodynamic diameter of 65 nm. This peculiar geometry was found to bind to tumor cells more efficiently in vitro because of multivalent interactions between the nanoworms and the cellular receptors, compared with spherical nanoparticle controls. The passive accumulation of the particles in vivo was also amplified for the nanoworms. In this article, the magnetic and relaxation properties of the nanoworms are presented and compared to those of classical contrast agents.

2. Materials and methods

Nanoworms were prepared using a modification of the synthesis of dextran-coated iron oxide particles, as previously described (10). A 0.63 g aliquot of FeCl3.6H2O and 0.25 g FeCl₂ 4H₂O were mixed with 4.5 g dextran in 10 ml of deionized (Millipore) water at room temperature. This acidic solution was neutralized by the dropwise addition of 1 ml concentrated aqueous ammonia under vigorous stirring and a steady purge of nitrogen, and it was then heated at ~70°C for 1 h. After purification by centrifuge filtering column (100 000 MWCO, Millipore), the magnetic colloid was crosslinked in strong base (5_M aqueous NaOH solution) with epichlorohydrin (Sigma) and filtered through a 0.1 μm pore diameter membrane (Millipore). Nanoworms with a size range of 50–80 nm were separated using a MACS® Midi magnetic separation column (Miltenyi Biotec). Transmission electron microscopy (TEM) observations were collected with a CM 20 Philips microscope. The hydrodynamic size of the particles was evaluated using Photon Correlation Spectroscopy (Zetasizer Nanoseries ZEN 3600, Malvern, UK).

Magnetometry curves (up to 8.5 T) were recorded using a quantum design physical property measurement system with the vibrating sample magnetometer attachment. Samples were measured at 37°C. The diamagnetic contribution of water was subtracted from the data obtained on a concentrated aqueous solution of magnetic nanoworms.

Small angle X-ray scattering (SAXS) was measured at the ID01 beamline at ESRF, Grenoble. A stabilized aqueous dispersion of the nanoworms was sealed in a quartz capillary and measured with an X-ray energy of 7.072 keV. Sample detector distances of 0.5 and 1.4 m allowed for data collection in the range of the wavevector Q of 0.08–2.5 nm^–1. SAXS gives an average statistically representative of about 1 mm³ of sample.

Relaxation time measurements were performed at low fields on Bruker (Germany) mq 20 and mq 60 instruments operating at magnetic fields (B₀) 0.47 and 1.41 T, respectively. Bruker AMX 300 (7 T) and AMX 500 (11.7 T) spectrometers were used for the high-field measurements. All these relaxometric measurements were performed at 37°C. T₁ nuclear magnetic relaxation dispersion (NMRD) profiles were recorded at sample temperatures of 5, 20 and 37°C, from 0.00023 to 0.23 Ton a Spinmaster fast field cycling relaxometer (STELAR, Mede, Italy). In most of the plots shown in this work, the magnetic field is expressed in terms of the proton Larmor frequency: a field of 1 T corresponds to a Larmor frequency of 42.6 MHz. The results are represented in terms of longitudinal and transverse relaxivities. The iron content of the sample was determined using inductively coupled plasma (ICP) spectroscopic analysis. Monte Carlo simulations of transverse relaxation induced by magnetic particles were performed as previously described (11).

3. Results

3.1. Physico-chemical characterization

The nanoworms display a distinctive worm-like morphology in the transmission electron microscope, with a length of approximately 50 nm (Fig. 1), as previously observed. The magnetic grains constituting the worms are ~5 nm in diameter. The average hydrodynamic diameter of the worms including the dextran coating is 71 nm.

Figure 1.

Transmission electron microscopy of the nanoworms, illustrating their elongated shape. The bar represents 50 nm.

The SAXS data exhibit the first form factor minimum of the spherical nanoparticles at Q = 1.8 nm^–1, which corresponds to an average diameter of 5 nm for single maghemite grain (Fig. 2).The observation of a minimum suggests a rather narrow size distribution of these spherical building blocks.

Figure 2.

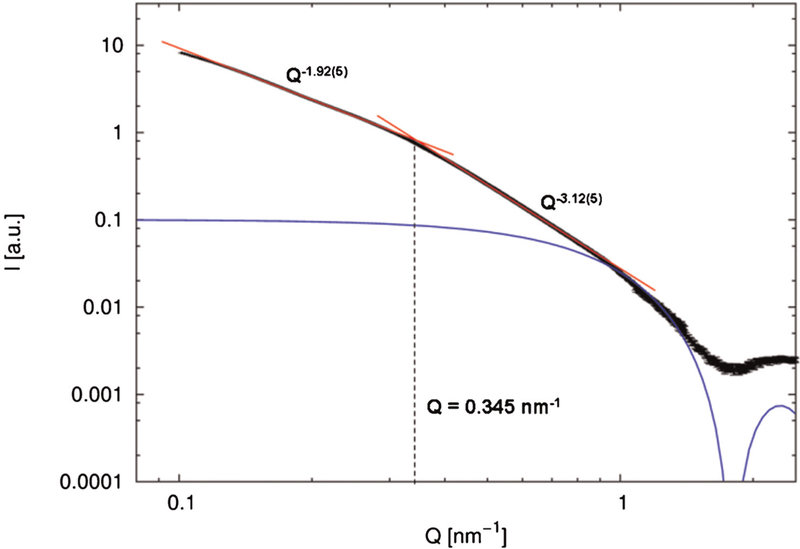
SAXS of iron oxide nanoworms. The simulated scattering form factor of spherical particles with a diameter of 5 nm is presented in blue. The two observed power laws are shown in red.

In the lower Q range, two different power laws for the Q dependency are observed. The intersection of both power laws at 0.345 nm^–1 leads to a Guinier radius of 18.2 nm for the clusters of nanoparticles. If the nanoworms are regarded as cylinders with a cross section of 5 nm, an average nanoworm length of 62 nm can be deduced from the Guinier radius (12).

The power law in the higher Q range (I ∝ Q^–3.12(5)) yields surface fractal dimension of 6–3.12 = 2.88, indicating a rough surface and a high branching of the nanoworms. The power law in the lower Q range (I ∝ Q^–1.92(5)) yields the mass fractal dimension of 1.92, which is close to the dimension of polymer chains exhibiting random walk and describes the soft aggregation of the nanoworms in the dispersion. Combining the high degree of branching of the nanoworms and the average length of 62 nm, we note a good agreement of the SAXS results with the hydrodynamic size of the worms.

3.2. Magnetometry

The magnetometry curve of the NWs was recorded using high field magnetometry (Fig. 3). A Langevin function was fitted to the data, providing a particle radius R of 3.5 nm and a saturation magnetization M_sat of 80.4 A m² kg^–1 (iron). However, the Langevin model did not fit the high-field data: the magnetization of the sample does not completely saturate and instead it displays a gradual increase. Therefore we used the sum of a Langevin function and a linear term for the fit:

$$M(B)=L(x)+\alpha B_0\text{with}x=\mu B_0/kT$$ (1)

where μ is the saturation magnetic moment and B₀ is the magnetic field. This function provided a satisfactory fit, yielding R = 4nm and M_sat = 74.9 A m² kg^–1 (iron), with α = 0.99 A m² [kg(iron) T]^–1. However, the irons ions responsible for the linear term are not supposed to contribute to the Langevin function. If we assign the linear contribution to paramagnetic ferric ions, as done by Bulte for MION-46L, it is possible to calculate the fraction of paramagnetic ions in a particle, knowing the paramagnetic susceptibility of Fe³⁺ (13). From this calculation, one can show that approximately 41 % of the ions are paramagnetic, which is in excellent agreement with the data obtained by Bulte (5). Since these ions are not involved in superparamagnetism, it allows calculating corrected values for the parameters of the Langevin function M_sat and R: one obtains M_sat = 128 A m² kg^–1 [iron] and R_S = 3.5nm. In this case, R_S represents the radius of the superparamagnetic core inside the particle, without the hypothetic paramagnetic shell. The saturation magnetization of this superparamagnetic core is really close to the maximum value for bulk magnetite.

Figure 3.

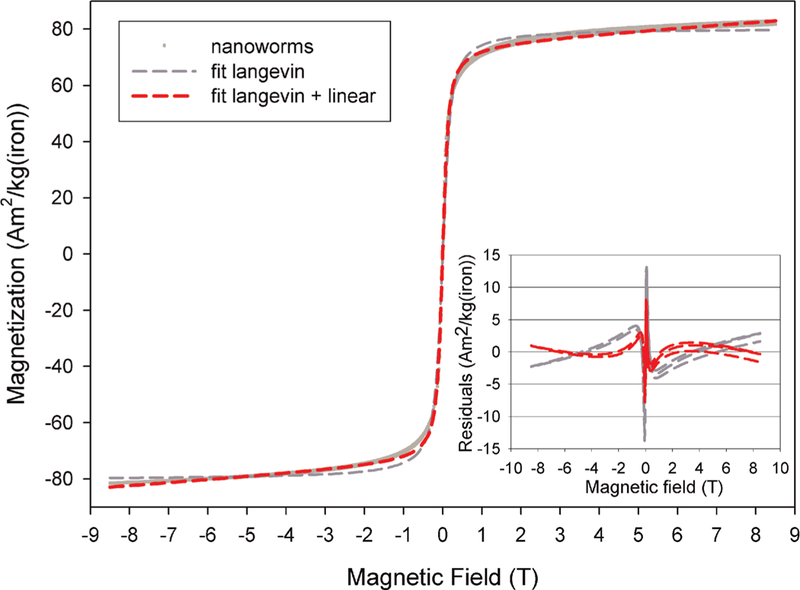
Magnetometric curve of nanoworms obtained at 37°C between –8.5 and 8.5 T. The inset shows the residuals of the fittings of the Langevin function and equation (1) to the data.

3.3. Relaxometry

Figure 4 displays the longitudinal NMRD profiles of the magnetic nanoworms for three temperatures. The shape of the profiles is typical of the relaxation induced by superparamagnetic particles (14). The data at 37°C were fitted to the theoretical relaxation model developed by Roch et al. (15), providing a crystal radius of 6.3 nm and a saturation magnetization of 50.9 A m² kg^–1 (iron). These values must be carefully interpreted since the theoretical model only provides realistic parameters for non-clustered systems. The relaxation rates of nanoworm solutions with various concentrations of iron have been measured for different magnetic fields. The corresponding relaxivities – the slope of the linear increase in the rate with the iron concentration – are listed in Table 1. Interestingly, the transverse relaxation rate increases with the magnetic field, even at high field.

Figure 4.

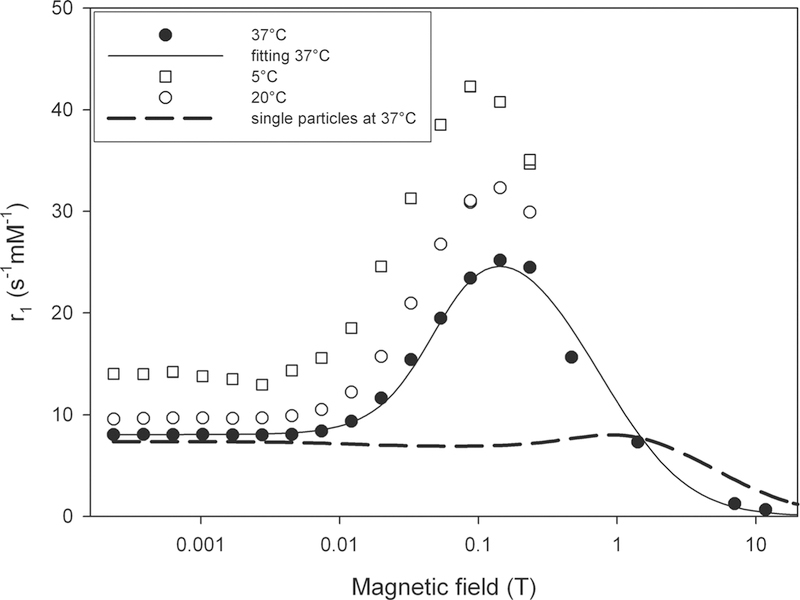
NMRD profiles of an aqueous solution of magnetic nanoworms obtained at 5, 20 and 37°C. The solid line is a fitting of the Roch model (15) to the data at 37°C. The dashed line represents the predicted theoretical NMRD curve for isolated particles, as described in the text.

Table 1.

Relaxivities of nanoworms at 37°C for different applied magnetic fields

Magnetic field (T)	r1 (s–1 mm–1)	r2 (s–1 mm–1)
0.47	15.59 ± 0.47	56.2 ± 1.7
1.41	7.24 ± 0.22	64.8 ± 1.9
7	1.030 ± 0.031	78.4 ± 2.4
11.7	0.657 ± 0.020	95.5 ± 2.9

4. Discussion

An interesting feature of the worms is the linear increase of the magnetization at high field, after the saturation of the super-paramagnetic particles. This could be due to the existence of a disordered paramagnetic fraction at the surface of the particles, as it has already been noticed for MION-46L by Bulte et al. (5). From a practical point of view, this explains the increase in the transverse relaxivity with the magnetic field since r₂ depends on the square of the magnetic moment of the particle. The previously reported transverse relaxivity of the worms was r₂ = 116 s^–1mM^–1 at 4.7 T and room temperature (10). As the relaxivity decreases with temperature, it is clearly consistent with the values obtained in the present work at 310 K: r₂ = 78.4 s^–1 mM^–1 at 7 T. The relaxivities of the nanoworms are typical of SPIOs (16), with an r₂/r₁ ratio at 1.41 T of ~9.

The nanoworms were developed to increase the targeting efficiency of magnetic particles to tumor tissues in vivo and in vitro. Interestingly, as it has been observed for SPIOs, the relaxation effect of iron oxide nanoparticles is more pronounced when they are structured in clusters (linear chains) than when they are in the form of isolated, single particles. Indeed, the isolated grains (nanospheres) were obtained by a classical synthesis (17), which makes them very similar to MION-46L. This is confirmed by the similar saturation magnetization of both compounds. Moreover, analysis of the nanospheres TEM pictures provides the same size distribution as MION-46L. For this latter contrast agent, whose relaxation has been intensively studied, r₂ = 34.8 s^–1 mM^–1 at 0.47 T and 37°C (6). It is 2 times smaller than the relaxivity of the nanoworms. In order to verify the increase of relaxivity due to the linear clustering, we have also performed numerical simulations of transverse relaxation. For particles of 5 nm diameter, with M_sat = 105 A m² kg^–1 [iron], one obtains r₂ = 17.6 s^–1 mM^–1 for the homogeneously distributed spheres and r₂ = 47.6 s^–1 mM^–1 for the linear chains of 15 particles in contact. The relaxivity increases by a factor of 2.7, which is in good agreement with our data. However, when normalized to the magnetization of our samples (M_sat = 74.9 A m² kg^–1 [iron]) the relaxivities obtained by the simulations become r₂ = 8.96 s^–1 mM^–1 for the homogeneously distributed spheres and r₂ = 24.2 s^–1 mM^–1 for the linear chains. These values are three times smaller than the measured ones. However, the simulation data of the relaxation induced by isolated spheres is confirmed by the well established outer sphere theory (3):

$$r_2=\frac{4}{135\pi }\frac{N_A}{N_{\mathrm{F}\mathrm{e}}}\frac{{\mu }_0^2{\gamma }^2}{RD}{[\mu (B)]}^2$$ (2)

where N_A is the Avogadro number, N_Fe is the number of iron atoms in one particle and D = 3 10^–9 m² s^–1 is the water diffusion coefficient at 37°C. For R = 2.3 nm, one obtains r₂ = 9.36 s^–1 mM^–1 for the nanospheres, which is in agreement with the simulation, but much smaller than the measured value. This underestimation could be due to the size distribution of the magnetic crystals. We have thus also calculated the relaxivity of a system of isolated particles with a Gaussian distribution of sizes: R = 2.3 ± 0.6 nm. These parameters of distribution were previously obtained for MION-46L from TEM pictures. One obtains r₂ =10 s^–1 mM^–1, which is still significantly smaller than the measured relaxivities. An explanation of the underestimation of the relaxation rate by the theory has been recently proposed by Carroll et al. (7)They proved that the size distribution of the magnetic particles obtained by TEM was not suited to estimate the relaxation rates. The size distribution obtained by SAXS on aqueous solutions of single particles should be used instead. Small clusters of particles are taken into account in the SAXS analysis on aqueous solutions, while they are not in the TEM analysis of dried samples. Using TEM or SAXS distribution parameters in the r₂ estimation led to a difference by a factor of about 3: the rates obtained with SAXS data were larger and thus closer to the experimental data, because of the large influence of small clusters on the relaxation rates. Our theoretical estimation of the transverse relaxation was performed with the size distribution obtained by TEM. It is thus logical that it underestimates the measured rates.

The nanoworms are thus effective T₂ contrast agents, especially at high magnetic field. Recently, Matsumoto et al. (18) also showed by computer simulations that the value of the transverse relaxation time of linear chains of six iron oxide particles of R = 11 nm is larger than for the isolated particles but is almost identical to the value for isotropic clusters, although a small decrease (18%) in the value of R₂ was observed. As a consequence, the linear geometry of the worms should not drastically affect their efficiency as relaxation agents, in comparison with spherical clusters.

By contrast, the longitudinal relaxivity of the worms is less than the predicted relaxivity of the isolated magnetic grains (dashed line, Fig. 4), calculated using a well-established relaxation model for the same grain characteristics (R = 2.3 nm,M_sat = 74.9 A m² kg^–1 [Fe])(15). This is consistent with a previous study on the effect of clustering on longitudinal relaxation induced by magnetic particles (19).

5. Conclusion

Beyond the enhanced targeting efficiency, the maghemite nano-worms present interesting magnetic properties. Their magnetization increases with applied magnetic field up to 8.5 T, which results in an appreciable increase in their transverse relaxivity at high magnetic fields. Because of their cluster morphology, the transverse relaxation is more efficient than for the unclustered magnetic grains. These nanoworms thus represent an interesting contrast agent for molecular and cellular imaging.