Attribute level overlap (and color coding) can reduce task complexity, improve choice consistency, and decrease the dropout rate in discrete choice experiments

Abstract

A randomized controlled discrete choice experiment (DCE) with 3,320 participating respondents was used to investigate the individual and combined impact of level overlap and color coding on task complexity, choice consistency, survey satisfaction scores, and dropout rates. The systematic differences between the study arms allowed for a direct comparison of dropout rates and cognitive debriefing scores and accommodated the quantitative comparison of respondents' choice consistency using a heteroskedastic mixed logit model. Our results indicate that the introduction of level overlap made it significantly easier for respondents to identify the differences and choose between the choice options. As a stand‐alone design strategy, attribute level overlap reduced the dropout rate by 30%, increased the level of choice consistency by 30%, and avoided learning effects in the initial choice tasks of the DCE. The combination of level overlap and color coding was even more effective: It reduced the dropout rate by 40% to 50% and increased the level of choice consistency by more than 60%. Hence, we can recommend attribute level overlap, with color coding to amplify its impact, as a standard design strategy in DCEs.

1. INTRODUCTION

Discrete choice experiments (DCEs) are frequently used in health economics to estimate health state utility and quality‐adjusted life year values (e.g., Bansback, Brazier, Tsuchiya, & Anis, 2012; Viney et al., 2014), patient and physician preferences for treatment options (e.g., Krucien, Gafni, & Pelletier‐Fleury, 2015; Rise, Hole, Gyrd‐Hansen, & Skåtun, 2016), and willingness to pay for various health services (e.g., Bosworth, Cameron, & DeShazo, 2015; Mentzakis, Ryan, & McNamee, 2011). The design of such DCEs involves a fundamental trade‐off between statistical efficiency and behavioral efficiency. On the one hand, a higher statistical efficiency results in more informative choice tasks and hence in a smaller required sample size (e.g., Bliemer & Rose, 2010; Huber & Zwerina, 1996; Kanninen, 2002; Sándor & Wedel, 2001). On the other hand, a higher statistical efficiency typically increases the level of task complexity and hence increases the likelihood of confusion or misunderstanding, reduces the level of choice consistency, reduces the total number of choice tasks that respondents can evaluate due to “respondent fatigue,” encourages simplifying choice heuristics, and increases the likelihood of respondents dropping out of the survey (e.g., Swait & Adamowicz, 2001; DeShazo & Fermo, 2002; Viney, Savage, & Louviere, 2005; Louviere, Islam, Wasi, Street, & Burgess, 2008; Johnson et al., 2013; Yao, Scarpa, Rose, & Turner, 2015; Flynn, Bilger, Malhotra, & Finkelstein, 2016; Jonker, Donkers, De Bekker‐Grob, & Stolk, 2018a). All of these aspects affect the amount of information per choice task, the feasible number of choice tasks in the DCE design, and sometimes the statistical model to be estimated, which is reflected in the conceptual framework as depicted in Figure 1.

Figure 1.

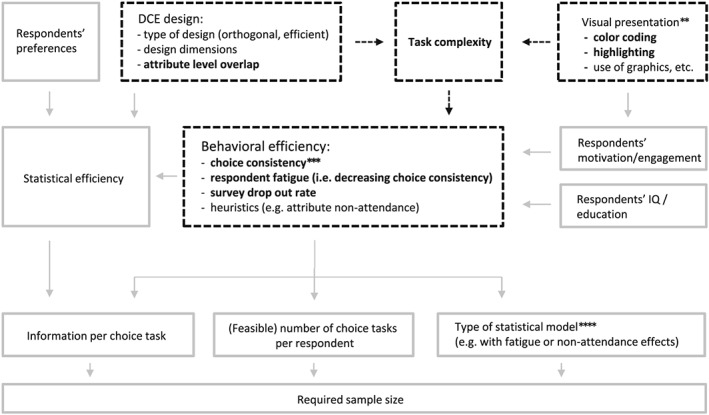
Conceptual model of the trade‐off between statistical and behavioral efficiency. The scope of analyses in this paper is indicated by the bold fonts and dashed lines and arrows. ^**The visual presentation can moderate the impact of task complexity on behavioral efficiency but may also affect respondents' motivation and engagement. These two pathways are not disentangled in this paper. ^***Statistical efficiency is determined by (a) the DCE design, (b) the type of statistical model to be estimated, (c) respondents' preferences (i.e., relative attribute and level importances), and (d) respondents' choice consistency. The latter explains the effect of behavioral efficiency on statistical efficiency. ^****Most efficient DCE designs are optimized for the standard conditional logit model, irrespective of the model actually expected to be estimated. Hence, there is (usually) no feedback loop from the type of statistical model to the DCE design. DCE: discrete choice experiment

Standard strategies to reduce choice task complexity—and thereby improve behavioral efficiency—comprise the reduction of the number of attributes and attribute levels (e.g., Bech, Kjaer, & Lauridsen, 2011; Caussade, de Dios Ortúzar, Rizzi, & Hensher, 2005; Louviere et al., 2008), the use of pairwise choice tasks as opposed to choice tasks with three or more choice alternatives (e.g., Hensher, 2006; Rolfe & Bennett, 2009), and the implementation of a clear and visually attractive presentation of the choice tasks (for example, with color codings and other visual aids; see, e.g., Hauber, Mohamed, Beam, Medjedovic, & Mauskopf, 2011; Gonzalez, Johnson, Runken, & Poulos, 2013; Mühlbacher & Bethge, 2015; Mühlbacher & Bethge, 2016). These strategies can be combined with DCE design optimization algorithms that avoid unrealistic attribute level combinations and/or impose a minimum number of attributes in each choice task to be at the same level, with the latter commonly referred to as attribute level overlap or simply level overlap (e.g., Kessels, Jones, & Goos, 2012; Maddala, Phillips, & Reed Johnson, 2003).

However, in real‐life applications, many of these strategies are difficult to use. For example, many DCEs require a relatively large number of levels to adequately capture the intrinsic complexity of the choice process under investigation. Also, in many health‐related applications, the number of attributes and levels are related to a particular instrument (e.g., EQ‐5D, SF‐6D, and ICECAP) and cannot be varied at all. Furthermore, pairwise choice tasks are already commonly used (Watson, Becker, & de Bekker‐Grob, 2017), which implies that the number of choice alternatives cannot be further reduced without changing the elicitation method (for example, by using single‐profile best‐worst scaling instead of a DCE). Finally, excluding a large number of attribute level combinations has a strong detrimental effect on statistical efficiency and can even compromise statistical identification, which cannot be remedied by an increase in the sample size and implies that only a small number of unrealistic combinations can be blocked in a DCE design.

The introduction of attribute level overlap, in contrast, is a practical and theoretically appealing approach to improve behavioral efficiency. Holding the levels of one or more attributes constant makes the choice tasks easier, which can improve choice consistency and reduce respondent fatigue. The introduction of sufficient attribute level overlap also discourages the use of dominant attribute strategies and can render simplifying strategies unnecessary, which significantly reduces attribute nonattendance (Jonker et al., 2018a). Indeed, with sufficient attribute level overlap, there will automatically be choice tasks in which the dominant attributes are fixed at identical levels, thereby forcing respondents to consider the remaining attributes (Kessels et al., 2012). Attribute level overlap thus allows DCE researchers to obtain preference information for all attributes that affect the choice process, even if some of these attributes are clearly less important in the choice process than others.

The visual presentation of choice tasks can also significantly reduce the task complexity and cognitive burden of the DCE design for respondents. For example, with the introduction of attribute level overlap, the visual design can help respondents to quickly identify the levels that are similar versus those that require additional attention because the attribute levels are different. This can be achieved by highlighting the attributes that are not overlapping (for example, by using different background colors, see, e.g., Norman et al., 2016; Mulhern et al., 2017) or, if the included attribute levels are strictly ordinal, via intensity color coding (e.g., traffic light colors or shades of purple; cf. Jonker, Attema, Donkers, Stolk, & Versteegh, 2017; Jonker, Donkers, De Bekker‐Grob, & Stolk, 2018b).

Thus far, ample evidence exists on the impact of DCE design dimensions on choice complexity (e.g., Caussade et al., 2005; Hensher, 2006; Louviere et al., 2008; Rolfe & Bennett, 2009; Bech et al., 2011; Dellaert, Donkers, & Soest, 2012), but systematic evidence about the impact of attribute level overlap and color coding on the level of task complexity and behavioral efficiency is surprisingly scarce. In this research, we therefore aim to evaluate the individual and combined impact of (a) attribute level overlap and (b) color coding using a randomized controlled experiment with five study arms. The systematic differences in experimental conditions between the study arms allow for a direct comparison of dropout rates and cognitive debriefing scores and for the identification of relative choice consistency using a heteroskedastic mixed logit model. This provides an ideal assessment of the relative impact and merit of level overlap and color coding and constitutes our recommendations regarding their application in DCE research.

2. METHODS

2.1. Randomized controlled experiment and hypotheses

A large sample of 3,320 respondents aged 18 years and older was randomly assigned to one of five experimental study arms comprising a control group and four experimental study arms (see Table 1), thereby systematically introducing and omitting level overlap and color coding in the DCE while keeping all other aspects of the survey identical. Making use of this randomized DCE, the following hypotheses were evaluated:

Hypothesis 1

The introduction of attribute level overlap, color coding, and/or attribute level overlap combined with color coding reduces the level of task complexity, resulting in (a) lower survey dropout rates and (b) improved cognitive debriefing scores.

Hypothesis 2

The introduction of attribute level overlap, color coding, and/or attribute level overlap combined with color coding increases the level of choice consistency in the DCE.

Hypothesis 3

The introduction of attribute level overlap, color coding, and/or attribute level overlap combined with color coding reduces respondent fatigue (i.e., resulting in a smaller reduction in choice consistency during the course of the DCE).

Table 1.

Dropout rate and descriptive statistics of completes and dropouts, by study arm

Study arm	Overlap	Presentation	Dropout rate	Variable	Completes					Dropouts[Link]
					N	M	SD	Min	Max	N	M	SD	Min	Max
1				Age	541	48	17	18	92	86	55	16	18	82
	No	No color	13.7% (base)	Male (dummy)		0.52		0	1		0.55		0	1
				Educ_low		0.32		0	1		0.55		0	1
				Educ_med		0.41		0	1		0.34		0	1
				Educ_high		0.27		0	1		0.12		0	1
2				Age	540	47	17	18	87	59	54	14	24	81
	No	Shades of purple	9.8%**	Male (dummy)		0.47		0	1		0.54		0	1
				Educ_low		0.32		0	1		0.37		0	1
				Educ_med		0.42		0	1		0.42		0	1
				Educ_high		0.25		0	1		0.20		0	1
3				Age	553	47	17	18	84	59	55	18	19	89
	Yes	No color	9.6%**	Male (dummy)		0.47		0	1		0.41		0	1
				Educ_low		0.34		0	1		0.49		0	1
				Educ_med		0.40		0	1		0.34		0	1
				Educ_high		0.25		0	1		0.17		0	1
4				Age	551	47	17	18	88	49	55	18	21	86
	Yes	Highlighting	8.2%***	Male (dummy)		0.48		0	1		0.59		0	1
				Educ_low		0.30		0	1		0.43		0	1
				Educ_med		0.41		0	1		0.41		0	1
				Educ_high		0.29		0	1		0.16		0	1
5				Age	546	49	17	18	98	43	59	15	21	82
	Yes	Shades of purple	7.3%***	Male (dummy)		0.48		0	1		0.56		0	1
				Educ_low		0.31		0	1		0.53		0	1
				Educ_med		0.45		0	1		0.30		0	1
				Educ_high		0.25		0	1		0.16		0	1

Dropouts occurring during the discrete choice experiment choice tasks.

^** Null hypothesis of equal proportions is rejected with p < 0.05 (one‐sided).

^*** Null hypothesis of equal proportions is rejected with p < 0.01 (one‐sided).

Based on the formal evaluation of these hypotheses, this paper aims to establish attribute level overlap and color coding as potential strategies to reduce the task complexity, increase the level of choice consistency, improve survey satisfaction scores, and decrease the dropout rate in discrete choice experiments.

2.2. The DCE design (with and without overlap)

To achieve a sufficient level of baseline task complexity, which is required to be able to establish incremental improvements in behavioral efficiency once attribute level overlap and color coding are introduced, the randomized DCE included relatively large number of 21 choice tasks per respondent and was based on a relatively complicated DCE instrument. The DCE instrument comprised five attributes with five levels per attribute and was based on the EQ‐5D‐5L, which is a generic health state instrument that comprises the dimensions “mobility,” “self‐care,” “usual activities,” “pain/discomfort,” and “anxiety/depression.” EQ‐5D‐5L health states are defined by selecting one of five levels from each dimension, with 1‐1‐1‐1‐1 denoting perfect health and 5‐5‐5‐5‐5 the worst possible health state. Health state preferences for the EQ‐5D‐5L were derived by asking respondents to repeatedly evaluate two hypothetical health states and indicate which one they prefer (see Figure 2). The observed discrete choices were used to estimate the latent preference weights that respondents used to trade‐off the various attribute levels of each EQ‐5D‐5L health state; always with the “no health problem” levels used as the reference category.

Figure 2.

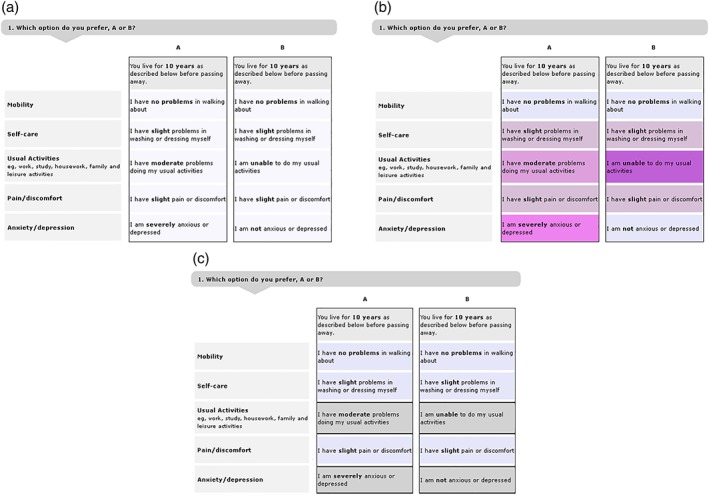
Visual presentation of the choice tasks. (a) “No color,” (b) “Intensity color coding,” (c) “Highlighting of differences” [Colour figure can be viewed at wileyonlinelibrary.com]

Bayesian efficient design algorithms were used to optimize two separate DCE designs: one with three attributes overlapped and one without attribute level overlap. Both designs were optimized based on the D‐efficiency criterion. To maximize the D‐efficiency of the designs while accommodating substantial respondent heterogeneity, heterogeneous DCE designs (cf. Sándor & Wedel, 2005) were used. Heterogeneous DCE designs consist of several subdesigns that are simultaneously optimized, but each participating respondent is only asked to complete a single subdesign, implying that no additional effort from individual respondents was required. As shown by Sándor and Wedel (2005), heterogeneous DCE designs can be substantially more efficient than homogeneous DCE designs, particularly when there is respondent preference heterogeneity and/or prior uncertainty about the preference structure.

The Bayesian design optimization algorithms were implemented in Julia (Bezanson, Karpinski, Shah, & Edelman, 2012). All designs were optimized for the standard conditional logit model based on a main effects utility function. The required prior preference information were obtained from previous EQ‐5D research and updated after a pilot run of 200 respondents per sample to maximize further improve statistical efficiency. The Bayesian D‐efficiency criterion was based on a Latin hypercube sample with 100 draws, optimized (also using Julia) to maximize the minimum distance between points. The optimization criterion was calculated as the weighted average Bayesian D‐efficiency of the 21 choice tasks per subdesign, with eight subdesigns per design and with ⅓ of the weight assigned to the combined (i.e., population) efficiency of the overall design and with ⅔ of the weight assigned to the individual D‐efficiencies of each of the subdesigns. Using such a weighted design criterion ensured that not too much individual level design efficiency was sacrificed to achieve a marginally higher overall design efficiency.

2.3. Visual presentation

The DCE design with and without attribute level overlap were both presented to respondents with and without color coding. Figure 2 shows an example of the different layouts used. As can be seen, the format without color coding uses no visual aids—except for a partially bold text that highlights the specific levels. The intensity color coding scheme implements the color blind optimized shades of purple as previously used by Jonker, Stolk, and Donkers (2012) and Jonker et al. (2017), with the darkest purple used to denote the worst and lighter purple used to denote better EQ‐5D levels. This color coding scheme has been specifically optimized to signal differences in attribute levels for individuals with red‐green color blindness (i.e., the most prevalent form of color blindness) while keeping the text readable for respondents who suffer from other forms of color blindness. Finally, the highlighting layout emphasizes the differences between choice options via the use of different background colors and bold black lines. This format inherently depends on some degree of overlap but, unlike intensity color coding, does not require or suggest an ordinal structure in the attribute's levels.

2.4. Respondent recruitment and survey structure

An online, nationally representative sample of 3,320 adult respondents (aged 18 years and older) from the Dutch general population in terms of age, sex, and education was recruited via Survey Sampling International. All respondents were Survey Sampling International panel members that received a small financial compensation for completing the survey. The sample size was intentionally large as to provide ample statistical power to detect all empirically meaningful differences between the study arms. A stratified sampling approach was used, meaning that participating respondents were randomly assigned to one of the study arms based on their age, sex, and educational attainment until prespecified (nationally representative) sampling quotas were filled, thereby mitigating the impact of selective dropout on the sample composition of the study arms.

The survey itself was structured as follows. First, the survey was briefly introduced, followed by a self‐rating question in which respondents were asked to rate their current health in terms of the EQ‐5D health dimensions. This procedure familiarized respondents with the format of the health states that were used in the questionnaire. Subsequently, two warm‐up questions were included that carefully explained the layout and the required trade‐offs of the DCE duration questions. Then, the actual set of 21 pairwise choice tasks were shown in a randomized order. To avoid too much repetition, a few background questions were included after DCE questions 7 and 14. Finally, at the end of the survey, respondents were asked several debriefing questions, including questions about the clarity and task complexity of the choice tasks and a ranking of the visual formats used in the surveys.

2.5. Statistical analyses

Starting with the statistical evaluation of Hypothesis 1, Fisher's exact tests of independence were used to compare the dropout rate as observed in the base case study arm and that in each of the experimental study arms. Furthermore, two‐sample t tests were used to compare the mean cognitive debriefing scores in the base case study arm and in each of the experimental study arms (cf. Lumley, Diehr, Emerson, & Chen, 2002; De Winter & Dodou, 2010). All calculations were performed using Stata 15 and one‐sided p‐values were used to reflect the (one‐sided) nature of the postulated hypotheses.

To be able to evaluate Hypotheses 2 and 3, a heteroskedastic mixed logit model was estimated using the choice data from all study arms. In the standard, homoskedastic MIXL model the utility for alternative j in choice task t for respondent i is typically modeled as the product of the health state characteristics (X _itj) and health state preference parameters (β _i). This results in the following utility function:

$$u_{\mathit{itj}}={\beta }_i·X_{\mathit{itj}}+{\epsilon }_{\mathit{itj}},$$ (1)

where ε _itj denotes the independent and identically Gumbel‐distributed error term. As a generalization of the specification used by Swait and Louviere (1993) and similar to models used by, for example, Sandor and Wedel (2005) and Louviere et al. (2008), this standard MIXL specification was extended with scale parameters λ that varied by study arm a and choice task t:

$$u_{\mathit{itj}}=\left({\beta }_i·X_{\mathit{itj}}\right)*{\lambda }_{\mathit{ta}}+{\epsilon }_{\mathit{itj}}.$$ (2)

More specifically, to be able to separately evaluate Hypotheses 2 and 3, the scale parameters λ _ta were defined as the product of two components, γ _a and δ _ta, with γ _a capturing the relative choice consistency within each study arm (i.e., relative to the average choice consistency of all study arms) and δ _ta reflecting the relative choice consistency achieved over the course of the DCE (i.e., from task t = 1 to t = 21, relative to the average choice consistency within each study arm):

$${\lambda }_{\mathit{ta}}={\gamma }_{\mathit{a}}*{\delta }_{\mathit{ta}}.$$ (3)

For statistical identification, a mean‐of‐one constraint was imposed on the γ _a parameters and, within each study arm a, on each set of δ _t parameters. Alternative constraints could have been used (see, e.g., the sensitivity analyses in the Supporting Information), but the implemented mean‐of‐one constraint has the benefit of multiplying the health state preferences by a scale parameter that is on average equal to one, thereby leaving the scale of the β parameters unaffected irrespective of the presence of choice consistency and fatigue effects. In order to increase statistical power and stabilize the estimates, the δ _t parameters were assumed to be identical for every three consecutive choice tasks (i.e., for tasks 1–3, 4–6, …, 19–21). Together with the randomization of the choice task order and the randomization of respondents across study arms, the implemented structure ensured sufficient statistical power and adequate statistical identification to be able to evaluate Hypotheses 2 and 3.

Conform standard MIXL assumptions, the respondent‐specific β parameters were assumed to be multivariate normal distributed with mean μ and covariance matrix Σ:

$${\beta }_i~\text{Multivariate Normal}\left(\mu ,\mathrm{\Sigma }\right).$$ (4)

Accordingly, the implemented model assumed that the underlying preference structure was unaffected by the introduction of level overlap and/or color coding. In the Supporting Information, this assumption was relaxed (as part of a wider set of sensitivity analyses), but these extensions had little impact on the presented results and no effect on the evaluation of the postulated hypotheses.

Bayesian methods were used to estimate the heteroskedastic MIXL models. All models were implemented in the BUGS language and fitted using the OpenBUGS software, making use of user‐written extensions to increase the efficiency of the Markov chain Monte Carlo sampling and implement the mean‐of‐one constraints on the scale parameters. The Supporting Information contains the exact model specifications, priors, and results of the sensitivity analyses. The latter confirmed that the presented results are not sensitive to the specification of the implemented priors on the scale parameters. All models were estimated using 15,000 burn‐in draws to let three Markov chain Monte Carlo converge and an additional 45,000 draws without thinning to reliably approximate the posterior distributions of the parameters. Convergence was evaluated based on a visual inspection of the chains and the diagnostics as implemented in the OpenBUGS software.

3. RESULTS

A total of 3,394 respondents were recruited to participate in the survey and randomly distributed across the study arms. Seventy‐four respondents indicated to be younger than 18 years old and were excluded from the analyses. The remaining 3,320 respondents resulted in 2,594 completes (78%) and in 726 dropouts (22%). Of these 726 dropouts, 293 (40%) already occurred during the introduction of the survey, 296 respondents (41%) dropped out during the DCE (more than half of which during the first three choice tasks), and another 137 respondents (19%) dropped out after having completed the DCE tasks due to browser incompatibility problems with the ranking task yet before having reached the cognitive debriefing questions. These 137 respondents were counted as completes in the DCE but not included in the other evaluations. The 2,594 respondents who did participate in the ranking task indicated to prefer the use of color coding: 59% preferred the shades of purple, 23% the highlighting of differences, and 18% preferred the format without color coding.

Table 1 presents the descriptive statistics of the survey respondents, broken down by study arm and DCE dropout status. As shown, respondents who dropped out were on average older and slightly lower educated, but there were no apparent systematic differences between the study arms, confirming the adequate level of randomization across study arms. As shown, the dropout rates varied between experimental conditions and the anticipated direction. The base case study arm (without overlap and color coding) had the highest dropout rate (14%), the study arms with either overlap or color coding had a lower dropout rate (10%), and the study arms with a combination of overlap with highlighting or color coding had the lowest dropout rate (8% and 7%, respectively). The Fisher's exact tests indicated that all reductions were statistically significant compared with the base case study arm. Accordingly, there was clear evidence that the introduction of overlap and color coding resulted in lower dropout rates.

Table 2 presents the mean cognitive debriefing scores, both separately for each study arm as well as aggregated by overlap and color coding condition. Interestingly, all of the observed differences were in the anticipated direction and mostly statistically significant. As shown, the introduction of level overlap and color coding improved the clarity of the questions, made it easier to identify the differences between choice options, made it easier to choose between the choice options, and reduced the level of agreement with the statement that there were too many choice tasks in the survey. Additionally, based on the combined study arm analyses, there was at least some indication that level overlap was primarily responsible for the lower choice task complexity whereas color coding had a particularly positive impact on the overall survey satisfaction. The latter would confirm the complementary effect of level overlap and color coding (i.e., not only on the dropout rate but also on survey evaluation scores).

Table 2.

Mean response scores of debriefing questions, by study arm and combined study arms[Link]

Study arm	Overlap	Color coding	The questions were clear	I could easily identify the differences between health states	I could easily chose between the health states	There were too many choice tasks in the survey	The survey's topic was interesting
				Separately for each study arm
1	No	No color	5.5 (base)	5.0 (base)	3.9 (base)	3.6 (base)	5.4 (base)
2	No	Shades of purple	5.6	5.1	4.1	3.6	5.5
3	Yes	No color	5.7**	5.4***	4.4***	3.3***	5.4
4	Yes	Highlighting	5.7*	5.4***	4.2**	3.3***	5.6**
5	Yes	Shades of purple	5.7*	5.4***	4.4***	3.3***	5.5*
				Separately by level overlap
1, 2	No	—	5.5 (base)	5.0 (base)	4.0 (base)	3.6 (base)	5.4 (base)
3–5	Yes	—	5.7***	5.4***	4.3***	3.3***	5.5
				Separately by color coding
1, 3	—	No	5.6 (base)	5.2 (base)	4.2 (base)	3.5 (base)	5.4 (base)
2, 4, 5	—	Yes	5.6	5.3**	4.2	3.4	5.6**

All answers were provided on 7‐point Likert response scales ranging from 1 (I totally disagree) to 7 (I totally agree).

^* Null hypothesis of equal means is rejected with p < 0.1 (one‐sided).

^** Null hypothesis of equal means is rejected with p < 0.05 (one‐sided).

^*** Null hypothesis of equal means is rejected with p < 0.01 (one‐sided).

Tables 3 and 4 together present the regression estimates obtained from the heteroskedastic MIXL model. Starting with Table 3, all EQ‐5D level decrements were logically consistent, had the expected sign, and were statistically significant (in the sense that the 95% credible intervals did not contain zero). Furthermore, there were substantial differences in the relative choice consistency between the study arms with all differences in the anticipated direction. As shown, the introduction of color coding had, as a stand‐alone strategy, no impact on the relative choice consistency. In contrast, the introduction of level overlap as a stand‐alone strategy increased the relative choice consistency by 33%. The combination of color coding and level overlap, however, was most effective and resulted in an increase in the relative choice consistency of approximately 64% for the highlighting and 67% for the shades of purple intensity color coding.

Table 3.

EQ‐5D level decrements and relative choice consistency between study arms

EQ‐5D level decrements	Population M (μ)	Population SD (sqrt [diag Σ])
Mobility 2	−0.31 [−0.37, −0.25]*	0.54 [0.46, 0.64]*
Mobility 3	−0.54 [−0.61, −0.47]*	0.84 [0.77, 0.93]*
Mobility 4	−1.68 [−1.77, −1.58]*	1.47 [1.38, 1.56]*
Mobility 5	−2.43 [−2.56, −2.30]*	2.23 [2.08, 2.41]*
Self‐care 2	−0.32 [−0.38, −0.26]*	0.44 [0.37, 0.54]*
Self‐care 3	−0.53 [−0.59, −0.46]*	0.65 [0.57, 0.71]*
Self‐care 4	−1.39 [−1.46, −1.30]*	1.15 [1.07, 1.25]*
Self‐care 5	−1.92 [−2.03, −1.82]*	1.70 [1.57, 1.83]*
Usual activities 2	−0.32 [−0.38, −0.26]*	0.46 [0.39, 0.52]*
Usual activities 3	−0.57 [−0.64, −0.50]*	0.67 [0.59, 0.73]*
Usual activities 4	−1.48 [−1.56, −1.39]*	1.17 [1.07, 1.30]*
Usual activities 5	−2.13 [−2.24, −2.02]*	1.76 [1.67, 1.86]*
Pain/discomfort 2	−0.43 [−0.49, −0.37]*	0.58 [0.51, 0.65]*
Pain/discomfort 3	−0.71 [−0.77, −0.64]*	0.88 [0.76, 0.99]*
Pain/discomfort 4	−2.20 [−2.31, −2.09]*	1.87 [1.76, 2.00]*
Pain/discomfort 5	−3.38 [−3.54, −3.23]*	2.82 [2.63, 3.00]*
Anxiety/depression 2	−0.48 [−0.55, −0.42]*	0.76 [0.68, 0.85]*
Anxiety/depression 3	−0.95 [−1.04, −0.87]*	1.34 [1.26, 1.42]*
Anxiety/depression 4	−2.37 [−2.52, −2.24]*	2.57 [2.41, 2.70]*
Anxiety/depression 5	−3.90 [−4.11, −3.70]*	3.97 [3.76, 4.22]*
Relative choice consistency	Scale parameters (γ)
γ 1 no overlap, no color	0.75 [0.70, 0.80]**
γ 2 no overlap, shades of purple	0.76 [0.71, 0.82]**
γ 3 overlap, no color	1.00 [0.93, 1.08]
γ 4 overlap, highlighting	1.23 [1.15, 1.32]**
γ 5 overlap, shades of purple	1.25 [1.17, 1.33]**

Note. Mean posterior estimates with 95% credible intervals (CI) in parentheses based on N = 2,731 completes.

^* 95% CI of μ does not comprise 0.0.

^** 95% CI of γ does not comprise 1.0.

Table 4.

Relative choice consistency over the course of 21 choice tasks

Study arm	1	2	3	4	5
Overlap	No	No	Yes	Yes	Yes
Presentation	No color	Shades of purple	No color	Highlighting	Shades of purple
δ tasks 1–3	0.83 [0.69, 0.97]**	0.80 [0.66, 0.95]**	1.09 [0.89, 1.32]	0.91 [0.74, 1.11]	1.04 [0.84, 1.26]
δ tasks 4–6	0.86 [0.72, 1.02]	0.90 [0.76, 1.06]	0.85 [0.68, 1.04]	0.79 [0.65, 0.95]	0.96 [0.79, 1.15]
δ tasks 7–9	1.04 [0.86, 1.25]	1.04 [0.87, 1.23]	0.99 [0.80, 1.21]	1.07 [0.87, 1.29]	0.99 [0.82, 1.20]
δ tasks 10–12	1.00 [0.83, 1.19]	0.93 [0.78, 1.10]	1.04 [0.85, 1.25]	0.87 [0.72, 1.05]	1.07 [0.88, 1.29]
δ tasks 13–15	1.03 [0.87, 1.22]	1.11 [0.93, 1.33]	1.11 [0.89, 1.38]	1.40 [1.13, 1.71]**	0.92 [0.75, 1.11]
δ tasks 16–18	1.18 [0.98, 1.40]	1.09 [0.90, 1.30]	0.94 [0.76, 1.14]	0.96 [0.78, 1.17]	0.91 [0.75, 1.10]
δ tasks 19–21	1.07 [0.89, 1.27]	1.14 [0.95, 1.36]	0.98 [0.79, 1.21]	1.00 [0.81, 1.21]	1.12 [0.91, 1.37]

Note. Mean posterior estimates of δ with 95% credible intervals (CI) in parentheses based on N = 2,731 completes.

^** 95% CI does not comprise 1.0.

Turning to Table 4, the presented results provide no evidence of respondent fatigue in any of the study arms, not even in the base case sample without attribute level overlap and color coding. However, Table 4 does highlight a consistent warm‐up and/or learning effect in the study arms without level overlap (i.e., Arms 1 and 2). Here, the choice consistency of the first three choice tasks was significantly below average (as indicated by the 95% credible intervals that do not comprise 1.0) whereas no such effect was present in the study arms that do include attribute level overlap (i.e., Study arms 3, 4, and 5).

4. DISCUSSION

4.1. Key findings

On the basis of a randomized controlled DCE with five study arms, we presented clear evidence that the introduction of attribute level overlap and color coding, both separately and combined, decreased the dropout rate, improved cognitive debriefing scores, and improved the level of choice consistency in the DCE. The introduction of overlap was already quite effective by itself; it reduced the dropout rate by 30%, increased the level of choice consistency by 33%, and removed all evidence of warm‐up and/or learning effects in the initial choice tasks. In contrast, the shades of purple intensity color coding reduced the dropout rate by 28% but did not have an effect on choice consistency or learning effect. Most importantly, the combination of overlap and color coding was particularly effective. Level overlap in combination with highlighting reduced the dropout rate by 40% and increased the level of choice consistency by 64%. The combination of overlap and intensity color coding was even slightly more effective; it reduced the dropout rate by 47% and increased the level of choice consistency by 67%.

At the same time, no evidence was found that the introduction of overlap and color coding had an impact on respondent fatigue. The latter is explained by the fact that there already was no sign of respondent fatigue in the base case study arm, which automatically precludes incremental reductions due to a decreased task complexity. On the one hand, this could be explained by the deliberate inclusion of a few non‐DCE questions after choice tasks 7 and 14, potentially having revealed an elegantly simple yet effective approach to include a large number of choice tasks without inducing fatigue effects. On the other hand, it could also indicate that respondents can simply handle many more choice tasks than typically used in applied research. The latter would be consistent with, for example, Carlsson and Martinsson (2008) and Hess, Hensher, and Daly (2012).

4.2. Limitations and future research

Although carefully designed, this study is not exempt from limitations, particularly with respect to the transferability of some of our results to other discrete choice experiments. For example, the presented evidence in this paper is based on the two different types of color coding that were included in the randomized controlled experiment. As such, the presented results may not be generalizable to other types of color coding schemes, such as, for example, traffic light color coding schemes. And even though the shades of purple color coding scheme was found to be particularly effective in combination with level overlap, the advantages of intensity color coding may be smaller in other DCEs. Unlike the highlighting of differences strategy, which is applicable to all attributes in any DCE with level overlap, the required ordinal structure of the attribute levels for intensity color coding is often only present in a subset of the included attributes, and the overall effect of color coding likely diminishes when applied to fewer attributes.

Another limitation is the transferability of the impact of attribute level overlap and color coding on the level of the dropout rate. As mentioned, the baseline dropout rate (in Study arm 1) was 14% during the DCE questions, which reduced to 7% with level overlap and intensity color coding (in Study arm 5). In comparison, the dropout rate in an online EQ‐5D study with 28 choice tasks fielded in the scientific LISS panel was only 1% (Jonker et al., 2017). The latter included both attribute level overlap and intensity color coding, which corresponds to a much (7×) smaller dropout rate. We suspect that the difference is partially sample specific (i.e., scientific vs. commercial) and perhaps also payment specific (i.e., several vs. less than 1 euro per survey), both of which would impact respondents (intrinsic/external) motivation. If so, the impact of overlap and color coding on the dropout rate may be stronger in commercial panels and particularly those with relatively small financial compensations for participating respondents.

Also the implemented econometric model has some limitations. For example, preferences and scale in discrete choice models are inherently confounded (Ben‐Akiva & Lerman, 1985), which means that the measurement of relative choice consistency between study arms crucially relied on the randomization of respondents across study arms. Despite this limitation and even though preferences and scale may indeed have been confounded, the carefully constructed randomized controlled experiment ensures that the substantial differences between the study arms originate (at least to a large extent) from the experimental conditions, because the confound will be constant across study arms.

Additionally, the relative choice consistency between samples was estimated under the assumption that the underlying preference structure remained identical in all study arms. The validity and impact of this assumption has been thoroughly evaluated in the Supporting Information. Interestingly, we do find that attribute level overlap and color coding had an impact on the estimated preference structure:

• Attribute level overlap reduced the emphasis that respondents place on the first and last attribute in the DCE. Without overlap, the first and last attribute typically receive the most attention from respondents, see, for example, Chrzan (1994), Kjær, Bech, Gyrd‐Hansen, and Hart‐Hansen (2006) and Auspurg and Jäckle (2017), and the introduction of overlap subsequently forces respondents to take all attributes into account and thus more equally divides their attention over all included attributes.

• Intensity color coding increased the distance between “slight” and “moderate” problems, which are notoriously difficult to distinguish in the Dutch translation of the EQ‐5D and more clearly separated when color coding was used. Given that illogical preference reversals were observed in the DCE results for three of the five dimensions in the official Dutch EQ‐5D valuation study for precisely these levels (Versteegh et al., 2016) and because color coding had no impact on the overall range of the preference estimates, we are inclined to consider this a beneficial outcome of color coding.

• Highlighting of differences reduced the emphasis placed on the moderate levels and increased the emphasis placed on the more extreme levels. The latter implies slightly different health state measurements relative to the results of the base case and intensity color coded study arms—without correcting an obvious baseline distortion.

Overall, we consider the impact of attribute level overlap and color on the preference structure to be positive, and more importantly, relaxing the assumption of an identical average preference structure in the study arms had a negligible impact on the evaluation of Hypotheses 2 and 3 and no impact on the presented conclusions.

Finally, an important avenue for future research concerns the determination of the optimal amount of attribute level overlap. For example, it would be interesting to investigate the extent to which attribute level overlap and color coding can be used to accommodate the elicitation of preferences from people that are traditionally excluded from health‐related DCEs and DCEs in general, for example, people with mild intellectual or cognitive impairment. In addition, it would be interesting to determine the optimal amount of level overlap when aiming to minimize the overall required sample size (instead of task complexity). Conform the conceptual framework presented in Figure 1 and as confirmed in the presented analyses, some of the reduction in statistical efficiency due to attribute level overlap will be compensated for by the increase in respondents' choice consistency. The latter results in larger β parameters that are further away from and consequently easier to establish as significantly different from zero. At the same time, attribute level overlap may increase the feasible number of choice tasks and avoid that more complex statistical models need to be estimated, which would further offset the negative impact of level overlap on the required sample size. On the basis of the results of Maddala et al. (2003), which used a minimum amount of overlap and found a relatively limited impact of overlap on choice consistency and statistical efficiency, we suspect that minimum overlap is not optimal. However, the maximum amount of level overlap as used in this research may unnecessarily decrease statistical efficiency and hence could also be suboptimal. If so, some intermediate amount of overlap would strike a better balance and further research is required to empirically establish the optimal amount of level overlap.

5. CONCLUSION

First, attribute level overlap is confirmed to be an effective strategy to improve the level of choice consistency and reduce the dropout rate. It also precludes the use of dominant attribute strategies, more evenly divides attention over all included attributes, and can reduce warm‐up and/or learning effects in the DCE. Accordingly, on the basis of the presented results and theoretical considerations, we recommend attribute level overlap as a default design approach to improve the quality and representativeness of the choice data. DCE designs with level overlap are supported by the Ngene (2017) software and several other design optimization packages, such as JMP (2018). Hence, DCE designs with level overlap are already accessible to DCE practitioners.

Second, the use of color coding has been established to amplify the effects of level overlap. When applicable to all attributes, intensity color coding is somewhat more effective than highlighting of differences, but highlighting can also be used in DCEs without an ordinal level structure. Highlighting of level differences may have a slight impact on the estimated preference structure, with less emphasis being placed on milder attribute levels and increased emphasis placed on more severe health problems. Accordingly, for DCEs with a clearly ordinal structure of the attributes' levels, we recommend the application of attribute level overlap in combination with intensity color coding.

DISCLAIMER

The views and opinions expressed in this article are those of the authors and do not necessarily reflect those of the EuroQol Group.

CONFLICTS OF INTEREST

The first and last authors are members of the EuroQol Group. The authors have no other conflicts of interest to report.

Supporting information

Figure S1. PDF of lognormal distribution (with μ = −0.08 and σ = 0.4, truncated between 0.1 and 10)

Table S1. EQ‐5D level decrements, relative choice consistency, and learning effects by sensitivity test

Table S2. Attribute level overlap and color coding scale effects

Table S3. Individual R‐squared estimates per study arm

Jonker MF, Donkers B, de Bekker‐Grob E, Stolk EA. Attribute level overlap (and color coding) can reduce task complexity, improve choice consistency, and decrease the dropout rate in discrete choice experiments. Health Economics. 2019;28:350–363. 10.1002/hec.3846