A Neural Model of MST and MT Explains Perceived Object Motion during Self-Motion

Abstract

When a moving object cuts in front of a moving observer at a 90° angle, the observer correctly perceives that the object is traveling along a perpendicular path just as if viewing the moving object from a stationary vantage point. Although the observer's own (self-)motion affects the object's pattern of motion on the retina, the visual system is able to factor out the influence of self-motion and recover the world-relative motion of the object (Matsumiya and Ando, 2009). This is achieved by using information in global optic flow (Rushton and Warren, 2005; Warren and Rushton, 2009; Fajen and Matthis, 2013) and other sensory arrays (Dupin and Wexler, 2013; Fajen et al., 2013; Dokka et al., 2015) to estimate and deduct the component of the object's local retinal motion that is due to self-motion. However, this account (known as “flow parsing”) is qualitative and does not shed light on mechanisms in the visual system that recover object motion during self-motion. We present a simple computational account that makes explicit possible mechanisms in visual cortex by which self-motion signals in the medial superior temporal area interact with object motion signals in the middle temporal area to transform object motion into a world-relative reference frame. The model (1) relies on two mechanisms (MST-MT feedback and disinhibition of opponent motion signals in MT) to explain existing data, (2) clarifies how pathways for self-motion and object-motion perception interact, and (3) unifies the existing flow parsing hypothesis with established neurophysiological mechanisms.

SIGNIFICANCE STATEMENT To intercept targets, we must perceive the motion of objects that move independently from us as we move through the environment. Although our self-motion substantially alters the motion of objects on the retina, compelling evidence indicates that the visual system at least partially compensates for self-motion such that object motion relative to the stationary environment can be more accurately perceived. We have developed a model that sheds light on plausible mechanisms within the visual system that transform retinal motion into a world-relative reference frame. Our model reveals how local motion signals (generated through interactions within the middle temporal area) and global motion signals (feedback from the dorsal medial superior temporal area) contribute and offers a new hypothesis about the connection between pathways for heading and object motion perception.

Introduction

To navigate through complex, dynamic environments, humans and other animals rely on the ability to perceive the movement of other objects during self-motion based on information in optic flow. When both the observer and an object are moving, the local retinal motion of the object differs in speed and direction compared with what would be experienced by a stationary observer. In particular, the object's retinal motion reflects the relative motion between the object and the observer: that is, object motion in an observer-centered reference frame. Nonetheless, it has been argued that important aspects of the avoidance and interception of moving objects rely on the visual system's ability to estimate object motion in a fixed (i.e., world) reference frame (Fajen, 2013; Fajen et al., 2013).

The optic flow field available to a moving observer comprises the sum of the global optic flow due to the observer's self-motion and the local retinal motion due to the object's movement. As such, if the visual system could identify the self-motion component and subtract it out, the world-relative motion of the object could be recovered (Fig. 1). The proposal that self-motion information is used to globally discount the component of the object's retinal motion due to self-motion has been termed flow parsing (Rushton and Warren, 2005) and represents the most well-established explanation to date of how the visual system recovers world-relative object motion. Flow parsing has been supported by a series of psychophysical experiments wherein subjects judged the direction of a vertically moving object on a computer screen while viewing optic flow patterns that simulate self-motion (Rushton and Warren, 2005; Warren and Rushton, 2007, 2008, 2009). As would be expected if the visual system “subtracted” the global optic flow pattern from the retinal optic flow, humans judge the vertical object trajectories as slanted. Although this “tilt effect” may seem to indicate a misperception in trajectory of the object, the direction of the perceived tilt coincides with the world-relative motion of the object, had the observer and object been moving through a 3D environment. For example, although the retinal motion of the object in the top panel of Figure 1 is upward (blue arrow), it would be perceived as moving up and to the left (red arrow), which is consistent with the object's motion relative to the world (bottom panel). As such, these findings can be interpreted as evidence of flow parsing.

Figure 1.

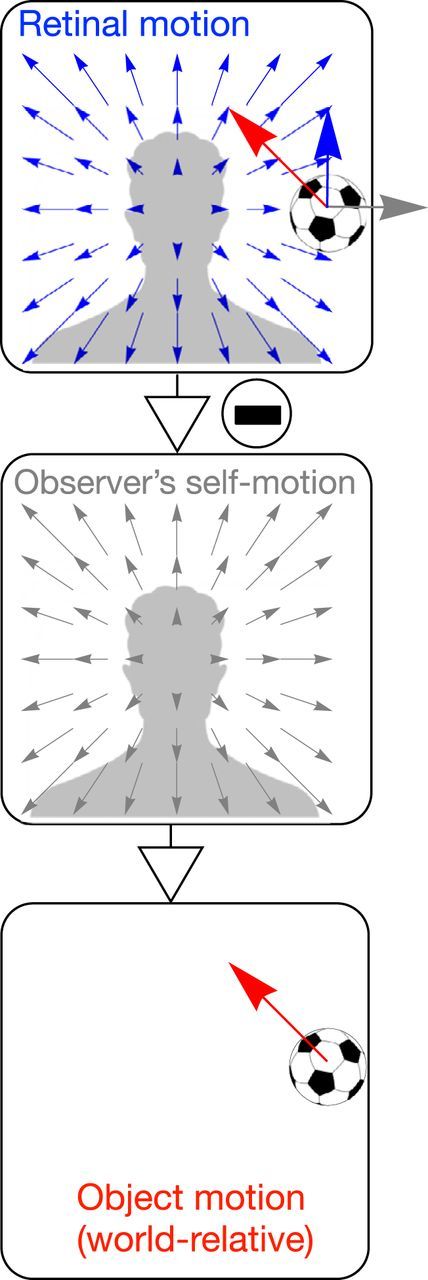
Depiction of flow parsing process whereby the component of optic flow due to the observer's self-motion on a straight-forward heading (middle) is subtracted from combined optic flow (self-motion + object motion; top). Red arrow indicates the object's motion independent of self-motion. Gray arrow indicates motion of background element at same location due to self-motion. Blue array indicates combined motion. Top, The object motion component and self-motion component sum to determine the object's retinal motion, which is directly upwards in this scenario. After the self-motion component is factored out, the resultant flow (bottom) reflects object motion in a world-fixed reference frame.

Although flow parsing captures the global influence of optic flow due to self-motion on the perception of object motion, the hypothesis is incomplete in several ways. First, the proposal does not shed light on the mechanisms within the visual system that underlie this process. It is unclear how such mechanisms identify the component of optic flow due to self-motion, how neurons perform the “subtraction,” at what stage this process occurs, and whether any other mechanisms are involved. Second, the hypothesis is qualitative, which makes it challenging to generate quantitative predictions. For example, it is unclear how to account for findings suggesting that flow parsing is incomplete, as if the proportion of optic flow that is discounted is <100% of that due to self-motion (Matsumiya and Ando, 2009; Dupin and Wexler, 2013; Dokka et al., 2015). Third, flow parsing is characterized as a process that relies on global rather than local flow and therefore does not explain the influence that motion immediately surrounding the object has on the object's perceived direction when the visual display does not contain a global optic flow pattern. For example, the fact that judgments of an object's motion are biased toward its world-relative trajectory, even when optic flow only appears within a small radius of the object (Warren and Rushton, 2009), cannot be explained by a mechanism that relies on global flow alone.

Here we propose two mechanisms on which the visual system might rely to recover world-relative object motion during self-motion. We built a neural model that implements these mechanisms, focusing on simplicity to capture the essential computational principles. We then simulated the model to allow for comparison with human psychophysical data on object motion perception.

Materials and Methods

Model overview.

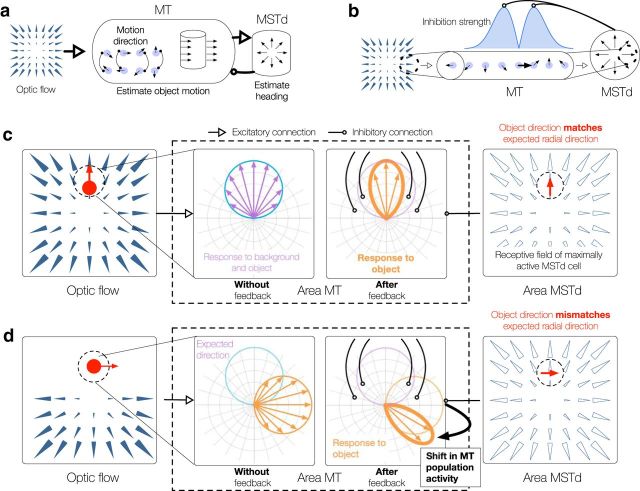
The model consists of two layers of neural units corresponding to the middle temporal (MT) and medial superior temporal (MST) visual areas of primate cortex (see Fig. 2a). MT units first respond to the direction (Albright, 1984) of moving dots presented to the model (“retinal flow”). MT projects to dorsal MST (MSTd), which contains heading-sensitive neurons tuned to the full-field patterns of radial expansion that one may encounter during forward self-motion (Duffy and Wurtz, 1991). Units in both model MT and model MSTd integrate motion, regardless of whether it corresponds to that of an object, the observer, or a combination of the two.

Figure 2.

a, Overview of proposed model of MT/MSTd. Rightward and leftward open arrows indicate feedforward and feedback projections, respectively. Thick open arrows indicate connections involved in MSTd-MT feedback mechanism. b, Illustration of the MSTd-MT feedback mechanism for region of optic flow field containing rightward motion (dashed circle). The rightward motion activates a MT unit tuned to that direction with a RF in the corresponding position (bold arrow). Units within the depicted MT macrocolumn have RFs indicated by the dashed circle. MT units with spatially overlapping RFs tuned to other directions within the same MT macrocolumn are quiescent. Only the MT unit tuned to rightward motion projects to the indicated MSTd unit (right), whose template matches the input. The other MT units within the macrocolumn are inhibited through feedback from the MSTd unit because their direction preferences locally differ from the one present in the radial template. The model proposes that “off-surround” directional inhibition is stronger for units tuned to directions similar to rightward and weaker for those with more dissimilar selectivities (blue curve). c, The directional signal within a MT macrocolumn is sharpened in the absence of a moving object or when a small object (red disk) moves in the same direction as the surrounding motion. Left, Retinal flow pattern, wherein an object (red disk) positioned straight ahead and slightly above the observer moves upward during forward self-motion (heading indicated by the central focus of expansion position). Polar plots in the center panels represent the local activation of MT units with a common RF indicated by the black dashed circle (left). Right, RF template of the maximally active MSTd unit. The retinal motion of the object (vertical red arrow) is superimposed on the MSTd RF. Left center, Broad ∼90° spread of activation in the MT directional macrocolumn in response to, for example, the object and background motion (purple). Because the retinal motion locally matches the template (right), the MT unit tuned to vertical motion is not inhibited through MSTd feedback, but units with similar directional preferences are (right center). d, Scenario in which an object (red disk) generates rightward retinal motion and the bottom hemifield contains radial motion that corresponds to straight-ahead self-motion (left). As in c, the polar plots in the center represent the local activation of MT units with a common RF indicated by the black dashed circle (left). Without feedback, MT units respond to motion in the retinal flow field (orange spread of activity; left center), which is influenced by both self or object motion. The activity peak within the MT macrocolumn shifts through feedback when the object motion locally mismatches the MSTd unit whose RF template is activated by the bottom radial hemifield. Rightward motion appears within the RF (orange spread of activity; left center), but upward motion is expected (light blue curve; center) in the MSTd template (right). The same MSTd unit is maximally activated as in c, even though the global optic flow appears only in the lower radial hemifield. MT units activated by the object and tuned to vertical components of motion are suppressed by feedback to a greater extent than units tuned to more dissimilar motion (right center). This leads to the relative enhancement of MT units tuned to motion toward the bottom right (bold orange; right center). The direction of the object signaled by the MT macrocolumn shifts from rightward (second panel) to the bottom right (third panel), which represents a shift toward the motion direction in a world-relative reference frame.

Two mechanisms are embedded within the model that together transform MT responses to object motion from an observer-relative reference frame into a world-relative reference frame: (1) feedback from MSTd to MT and (2) inhibition within MT. When an object moves along a direction that deviates from the optic flow generated by the observer's self-motion, MT units with receptive fields (RFs) that overlap with retinal flow from the object initially respond most strongly to the direction of retinal flow (i.e., sum of observer and object motion). Over time, the two aforementioned mechanisms shift the responses of these MT units toward the direction of the object motion in a world-relative reference frame. The mathematical details of the model are presented next. However, we encourage readers to jump to Results to develop an intuitive understanding of the model first.

Model specification.

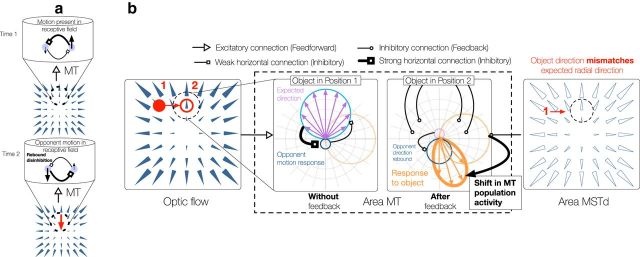
We computed the response of model MT units according to three processing stages. First, each MT unit received a directional input signal, which we obtained by comparing the unit's preferred direction to that in the optic flow field. Second, the signal was divisively normalized across direction, and feedback from MSTd that had an inhibitory effect was incorporated (see Fig. 2; Feedback from MSTd to MT). Finally, MT units tuned to opponent motion directions competed with one another (see Fig. 3; Interactions within MT).

Figure 3.

a, When an object moves downward (red arrow; bottom panel) and locally occludes the upward motion in the background radial pattern at Time 2, the unit that responded to the upward motion at Time 1 (bold arrow; top panel) becomes quiescent. The unit tuned to downward motion becomes active because its preferred motion appears within the RF (dashed circle), and it no longer receives inhibition from the unit tuned to upward motion (bottom panel). The release from inhibition leads to a transient rebound in activity in the unit tuned to downward motion. The RF of MT units within each column is depicted by the dashed black circle. b, Illustration of the opponent direction disinhibition mechanism interacting with MSTd/MT feedback when an object generates rightward retinal motion (red; left panel) and occludes vertical motion (position 2) in the background radial pattern that arises due to the observer's straight-ahead self-motion. As in Figure 2, polar plots in the center panels represent the local activation of MT units whose RF is indicated by the dashed black circle in the leftmost panel of Figure 2b. Right, RF template of the maximally active MSTd unit. The retinal motion of the object (rightward red arrow) is superimposed on the MSTd RF. Before occlusion (object in position 1), MT units respond to the vertical motion (purple arrows; second panel) within their RFs (position 2). Orange circle represents hypothetical response to the rightward object in the absence of surrounding motion. Because the rightward motion locally mismatches the global motion template (right), MSTd/MT feedback based on when the object was in position 1 shifts the direction signaled by the MT macrocolumn toward the bottom right (as in Fig. 2d). In addition, the occlusion of the upward motion results in rebound disinhibition of units tuned to the opponent downward direction (as in Fig. 3a). Units tuned to directions sharing a greater downward component are more disinhibited than those that are not, which shifts the population activity downwards (thick orange), even further away from the local upward motion of the template (compare right MT panel with that of Fig. 2d). The disinhibition occurs because the MT response interacts with that generated before the object entered the RF (object in position 1).

A core prediction of the model is that the recovery of object motion in a world-relative reference frame depends on a temporal solution within area MT. Whereas initial MT activity reflects the retinal pattern of motion (i.e., motion in the observer's reference frame), MT responses shift over time through feedback from MSTd and interactions within MT to align with the world-relative motion. To capture this in the model, MT responses depend on the optic flow field at the present time (t) and on the feedback and lateral interactions, computed based on the optic flow at the previous instant (t − 1).

Model MT.

We first computed the directional input M_d,x,y⁰ to an MT unit tuned to motion in one of 24 (D) equally distributed directions d whose RF is centered on position (x, y) using a rectified cosine as follows:

where θ is the angle of the analytical optic flow vector from a visual display (“Global,” “Local,” “Same,” “Opposite,” “Full”) from Warren and Rushton (2009) and [·]⁺ indicates half-wave rectification.

Next, we normalized the the directional signals generated by the first stage across direction at each visuotopic location (x, y).

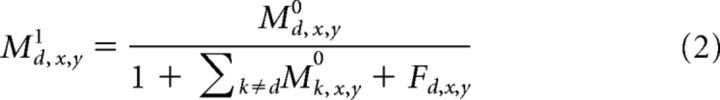The sum in the denominator of Equation 2 normalizes each directional signal according to the energy distributed across all preferred directions within an MT macrocolumn, and F_d,x,y indicates the feedback sent from MSTd, which has an inhibitory effect (defined below).

We computed the MT response after factoring in the inhibition each unit receives from the unit tuned to the opponent motion direction (180° difference). Because of the tonic nature of the inhibition, we modeled the short-term changes in the synaptic efficacy based on the limited availability of neurotransmitter: tonic inhibition degrades the efficacy of each connection as the amount of transmitter depletes and the efficacy improves over time while the unit is quiescent (Kim and Francis, 1998). For simplicity, we maximally depressed the efficacy of each active unit's inhibitory connection in the preferred motion direction and habituated the efficacy in similar directions ω to a lesser extent after signaling occurred at the given time step. This relationship can be expressed with the following kernel:

where H_d,x,y models the efficacy of the synapse. And s controls the extent signals from units with similar motion directions are habituated. We set s = 4 because this ensured that habituation generalized to cells with similar direction preferences (SD 65°).

The response of each MT unit is computed by the following equation:

where d indicates the opponent motion direction.

The synaptic efficacy changes from one time to the next according to the following:

where k specifies the rate of temporal accumulation, which we set to 0.75.

Model MSTd (feedforward).

Model MSTd responses are obtained by matching the responses of MT units against a regular grid of 1024 (R) radial templates that differed in the singularity position to which they are tuned. We refer to these templates as “feedforward templates” to differentiate them from the “feedback templates” between areas MSTd and MT that will be described in the following section. The following equation describes the pattern of radial expansion (A) that characterizes each MSTd template:

where (x₀, y₀) indicates the preferred FoE position. To match the radial pattern A_x0,y0,x,y with the responses generated by the 24 directional cells within each MT macrocolumn, we created 24 feedforward radial templates, each of which pools over a particular MT directional signal when it appears within the “sector” of the visual field that is consistent with radial expansion. For example, the rightward motion template pools the responses of MT cells tuned to rightward motion when their RFs coincide with the right side of the visual field. The following equations define the feedforward templates Td_0,y0,x,y (Eqs. 7,8) that integrate MT cells tuned to direction d, which are normalized by the number of pooled cells (Eq. 9):

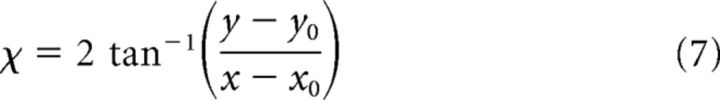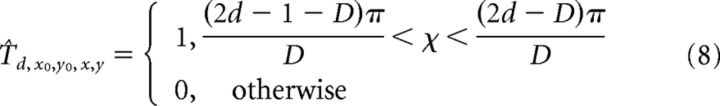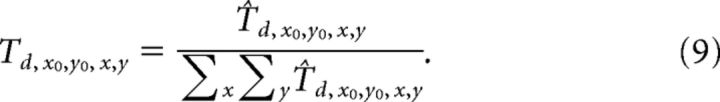Equation 10 describes the response of model MSTd (S_x0,y0), which is the match between the radial feedforward templates (T_d,x0,y0,x,y) and MT cells (M_d,x,y²). Each feedforward template integrates MT responses with greater weight near the preferred singularity position (x₀, y₀), and the weights decrease exponentially with distance (Layton et al., 2012; Layton and Browning, 2014).

In Equation 10, the parameter r influences the extent over which each MSTd integrates MT responses across visuotopic space and λ controls the overall gain of the feedforward signal.

Model MSTd (feedback).

In this section, we describe the MSTd feedback signal (F_d,x,y) that has an inhibitory effect on MT cells. The feedback signal received by each MT cell M_d,x,y² depends on three factors: the similarity between the MT cell's preferred direction (d) and the expected direction in the radial MSTd template (φ), the activation of the MSTd cell sending the feedback (S_x0,y0), and the visuotopic distance between the RF centers of the MT and MSTd cells.

We begin by describing how the directional similarity between the MSTd template and the MT cell affects the feedback signal (see Fig. 2b). The feedback equals zero when the directional tuning of an MT cell matches the direction within a feedforward MSTd template (i.e., no inhibition). MT cells tuned to neighboring directions within the same macrocolumn are, however, inhibited (i.e., strong inhibition targets neighboring directions). The inhibition drops off for MT cells with more dissimilar preferred directions (i.e., weaker inhibition targets more discrepant directions). We used a full-wave rectified sinusoid weighting kernel K_φ,d (Eq. 11; for example, see Fig. 2b) to quantify this pattern of inhibition, where φ corresponds to the “expected” motion direction within the MSTd template at position (x, y) and d indicates the direction of the MT cell that receives the feedback whose RF is centered on (x, y). Figure 2b depicts an example of K_φ,d when φ and d both correspond to rightward motion (i.e., the expected template direction matches the MT activation pattern).

The following equation describes the complete feedback signal (F_d,x,y) sent to the MT cell M_d,x,y².

where we use the MSTd activation on the previous time step S_x0,y0 (t − 1) to account for signal delays between MSTd and MT. The exponential in Equation 12 gives greater weight to feedback from MSTd cells with more distant RF centers (opposite the feedforward pattern), which implements the ecological tendency for optic flow due to self-motion to appear faster on the periphery. The outer summation combines the signals from all the MSTd units that send feedback.

Visual displays.

To generate quantitative predictions about the roles of each mechanism when estimating an object's trajectory during self-motion, we simulated the model under a range of conditions in which the area and location of the radial optic flow due to the observer's self-motion varied with respect to the motion of a small object. These conditions assess the contributions of each mechanism because MSTd-MT feedback depends on global motion signals integrated across the entire visual field, which is dominated by the optic flow generated by the observer's self-motion, whereas the opponent direction disinhibition mechanism depends on local motion signals derived from MT cells that share overlapping RFs. To facilitate comparison with human judgments, we used the optic flow displays (30° × 30°) from the “Full,” “Local,” “Global,” “Same,” and “Opposite” conditions in the psychophysical experiments of Warren and Rushton (2009). In these conditions, subjects judged the direction of a small target moving as different portions were revealed of a field of radial motion that simulated forward self-motion toward a frontoparallel plane.

We implemented the displays according to their published specifications with the following exceptions. First, we represented the moving target as a 1° square object rather a single dot so that it would activate more than one MT macrocolumn. Second, we restricted the object to begin moving perpendicularly with respect to the background radial optic flow pattern, whereas Warren and Rushton (2009) included ±15° trajectories. We tested a wider range of relative trajectories in a separate set of simulations (see Fig. 5) in which the object moved along 0°-360° trajectories in 15° increments relative to the background flow pattern in the “Full” condition.

Figure 5.

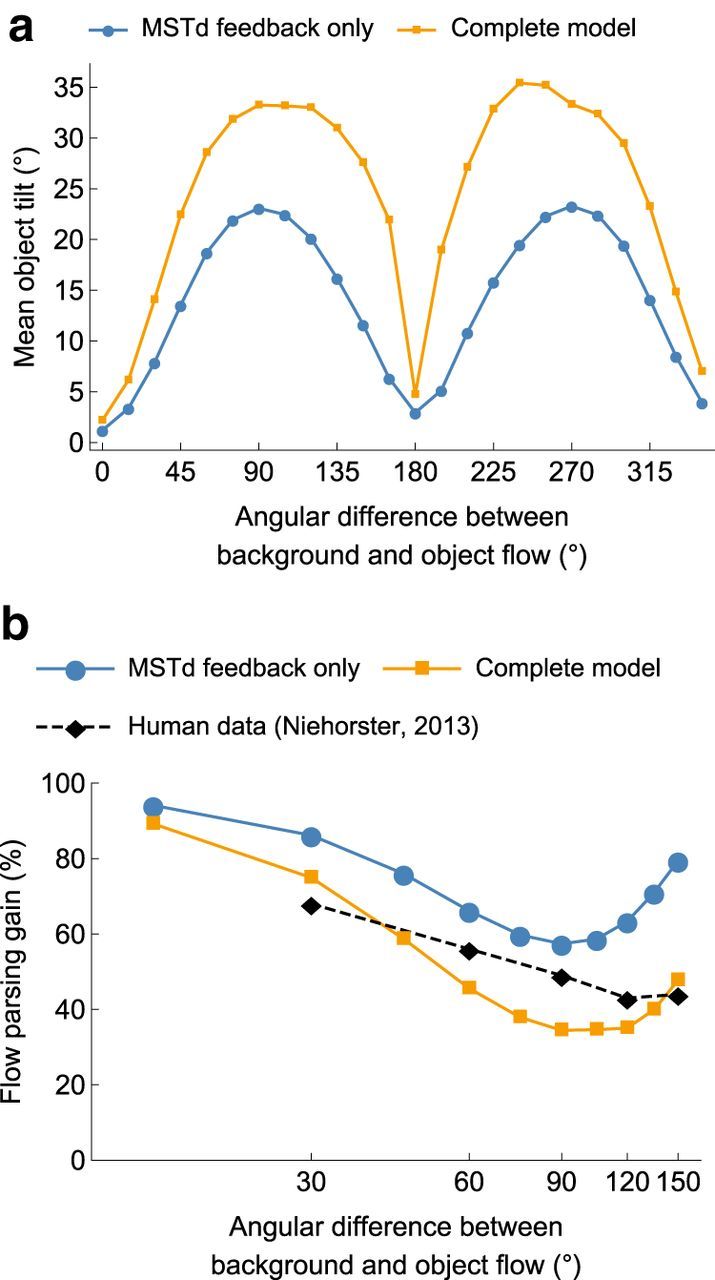
Model trajectory angle estimates for objects that move along different directions relative to the background retinal flow field. Displays were otherwise identical to those in the Full condition. Orange curves represent estimates produced by the Full model with both mechanisms (MSTd-MT feedback and interactions within MT). Blue curves represent estimates produced by a version of the model that contains only MSTd-MT feedback. a, Mean model trajectory estimates. b, Comparison between model estimates and human judgments under similar conditions, using the flow parsing gain measure.

Model estimate of object motion direction.

The deviations between human judgments and the on-screen direction of the target in the experiments of Warren and Rushton (2009) are consistent with the perception of object motion in a world-relative reference frame (Fig. 1). We used a three step procedure to obtain corresponding estimates of the object's direction (θ̂) based on the model MT population activity. First, we derived a population vector P⃗ based on the 24 (D) directional signals within each MT macrocolumn as follows:

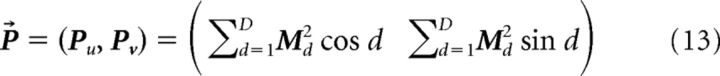Second, we averaged the direction of the population vectors from the N MT macrocolumns for which RFs coincided with the interior of object (O) as follows:

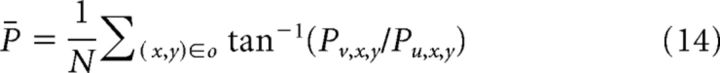Third, we subtracted the object's on-screen direction d_o with the model estimate P̄ to obtain the model's estimate of the object direction of motion (θ̂):

To compare the relative influence of the two model mechanisms in transforming object motion from an observer to world reference frame, we also computed the estimated object direction without (θ̂_MSTd) the effects of opponent direction disinhibition in MT by substituting M¹ for M² in Equation 13. In other words, θ̂ gives an estimate of the object that incorporates both mechanisms, whereas θ̂_MSTd only accounts for the influence of MSTd-MT feedback. We calculated the proportion accounted for by interactions within MT (“% MT Mechanism”) using the following equation:

Model estimate of flow parsing gain.

For simulations that focus on the relative motion between the object and the background radial motion, we computed the “flow parsing gain” (g), or degree to which the object motion was transformed into a world reference frame, which in humans is known to be incomplete when based entirely on monocular vision as follows:

The flow parsing gain in Equation 17 depends on v_f, the magnitude of the background radial self-motion, and v_n, the magnitude of the “remainder” vector that, when added to the one corresponding to the self-motion of the observer, yields the component discounted from the retinal flow to obtain the perceived object motion (Niehorster, 2013). Higher gains indicate that the magnitude of the residual vector is much smaller than that of the self-motion vector (v_n ≪v_f), meaning that the visual system deducts a larger portion of the observer's self-motion from the retinal flow field. On the other hand, lower gains indicate that the magnitude of the residual vector is similar to that of the self-motion vector (v_n ≈ v_f), meaning that the visual system deducts a smaller portion of the observer's self-motion from the retinal flow field. The only modification that we made compared with the other “Full” condition simulations was that we matched the local speed between the object and background flow. This allowed us to compute the flow parsing gain according to Eq. 17, using a “remainder” vector v_n based on the object's speed and estimated direction (Eq. 15).

Simulation conditions.

We implemented the optic flow displays and model in MATLAB R2015b (The MathWorks). We selected parameter values based on their physiological plausibility rather than optimize the model fit to the Warren and Rushton (2009) data without regard for the correspondence with physiology. For example, we configured model MSTd units to pool broadly over MT units (r; 20° SD), which is consistent with the large RFs of MSTd neurons (Duffy and Wurtz, 1995), and we set MT units to interact over a range of directions (s; 65° SD), which is consistent with the broad directional tuning of MT neurons (Albright, 1984). The model's transformation of an object's retinal motion into a world-relative reference frame (see Figs. 2, 3) was not particularly sensitive to changes in parameter values, and the model's qualitative correspondence to the psychophysical data was robust, as long as the parameter settings maintained the general properties described in Results (e.g., large MSTd RF sizes, broad MT directional tuning). A full description of model parameters and the values used in simulations is provided in Table 1.

Table 1.

Model parameters and their descriptions

Parameter	Value	Description
D	24	MT directional tuning quantization of 15°
R	1024	Number of MSTd templates spaced along a regular grid across the visual field
s	4	Extent that habituation of MT transmitter gates generalizes to MT cells with similar direction preferences (65° SD)
k	0.75	Rate of temporal accumulation in MT transmitter gates
r	0.01	Spatial extent (20° SD) of interaction between MSTd and MT cells (feedforward and feedback)
λ	675	Gain on feedforward MSTd signal from MT
h	2	Spread of inhibition toward MT cells tuned to directions neighboring the expected direction (45° SD) from the template of MSTd cell sending the feedback signal

Results

Feedback from MSTd to MT

The first of the two mechanisms for transforming object motion from an observer-relative to a world-relative reference frame is feedback from MSTd that influences the population activity in MT. Consider a MSTd unit that responds optimally to the pattern of motion generated by self-motion along a central heading (Fig. 2b). Within its RF, the MSTd unit locally integrates signals from individual MT units tuned to the direction that best matches the global template for radial expansion. For every MT unit that projects to the MSTd cell, there are a number of others within the same MT macrocolumn (i.e., units that share the same RF position but differ in directional selectivity) (Born and Bradley, 2005) that do not project to that MSTd cell because the preferred direction does not match the radial template. We propose that feedback from MSTd inhibits these units whose directional preference mismatches the radial template.

Before explaining the role of the feedback mechanism in recovering an object's world-relative motion, we briefly describe a second function served by this mechanism: to improve the quality of heading estimates in MSTd. Motion estimates early the visual system are contaminated by noise and subject to the aperture problem (Wallach, 1935; Marr and Ullman, 1981; Pack and Born, 2001), which may yield uncertain heading signals. The feedback mechanism mitigates this problem by enhancing the precision of the MT motion signal and the heading estimate in the absence of a moving object or when the object moves consistently with the background (see Fig. 2c).

Next, let us consider the effects of the MSTd-MT feedback mechanism when moving objects are present that generate retinal motion that is locally discrepant with the global motion pattern. Figure 2d (left) depicts such a scenario wherein the upper hemifield contains a rightward moving object and the bottom hemifield contains radial motion that corresponds to straight-ahead self-motion. Figure 2d (middle panels) depicts the response of MT units with RFs that overlap with the region of local motion from the object (i.e., a small portion of the full visual field depicted in the left panel). As the left center panel indicates, the MT response initially reflects the retinal flow pattern, which is determined by the sum of observer and object motion. The rightward motion signaled by MT units (Fig. 2d, left center, orange curve) mismatches the local direction of motion expected within the MSTd template that is activated by the radial pattern in the lower hemifield (Fig. 2d, right). The MT units signaling rightward motion are therefore inhibited through the proposed feedback mechanism because their preferred directions locally mismatch the upward direction in the global motion template.

Recall that the strongest inhibition targets MT units tuned to directions that are similar but not identical to the “expected” direction in the global motion template, and that inhibition of more dissimilar directions is weaker (Fig. 2b). Consequently, the subset of MT units that responded to the moving object and are tuned to motion with a more upward component receive stronger inhibition, as illustrated in Figure 2d (right center panel). This in turn changes the direction of object motion signaled by the MT macrocolumn compared with that in the retinal motion. As illustrated in Figure 2d (right center panel), this shift is away from the expected local direction within the global template and coincides with a bias toward the direction of object motion in a world reference frame (Warren and Rushton, 2009).

Although MSTd sends feedback that inhibits units in MT, the inhibition does not affect the driving (feedforward) signal to the most active MSTd units. This is because the inhibition targets units tuned to directions that mismatch the feedforward MT-MSTd RF (i.e., units other than those that drive the MSTd unit sending the inhibition). The simultaneous activation of units in both MT and MSTd carries the important implication that heading signals in MSTd are not compromised, even though they are involved in the transformation of retinal object motion into a world-relative reference frame.

In summary, the proposed MSTd-MT feedback mechanism improves the quality of heading estimates and biases the activity of the MT population responding to an object in the direction of the world-relative motion. Although initial MT unit responses simply reflect the retinal motion of the observer or object in an observer-relative reference frame, feedback from MSTd induces a directional shift only in MT units responding to motion of an object because the signal direction mismatches the global pattern. This shift is consistent with the discounting effect of the global motion pattern proposed by flow parsing.

Interactions within MT

Although global interactions dominate the influence of background optic flow on perceived object motion, the effect is slightly weaker when the region surrounding the object does not contain motion (Warren and Rushton, 2009). This finding suggests that the influence of the global motion pattern alone cannot fully explain the world-relative perception of object motion and that local interactions also play a role. We propose a second mechanism that complements MSTd-MT feedback: opponent direction disinhibition within MT. Within an MT macrocolumn, units tuned to opponent directions inhibit one another (Fig. 3a) (Qian and Andersen, 1994; Heeger et al., 1999). As depicted in Figure 3b, when a discrepantly moving object occludes motion belonging to the background, inhibition within MT results in rebound (increased) activity in the unit tuned to the direction opposite the occluded motion. The unit tuned to the background motion becomes quiescent after the occlusion occurs, which releases the unit tuned to the opponent direction from tonic inhibition, resulting in disinhibition. The mechanism yields rebound activity in the opponent directions relative to those within the global MSTd template (Fig. 3b). The rebound activity increases the directional shift produced by MSTd-MT feedback, leading to a more complete recovery of the world-relative motion of the object.

It is important to point out that the disinhibition of opponent motion signals only results in rebound activity when a moving object enters or exits the MT RF and moves along a direction that deviates from the background. When the retinal flow only contains motion arising from the observer's movement (e.g., Figs. 2c, 3a, top), MT directional responses are consistent over time. Although there may be a spread in the activation within an MT macrocolumn, responses to the direction opposite that which is dominant are weak (Fig. 2c, left center) and disinhibition does not affect the overall pattern of activity. Moving objects that enter or leave the RF may, however, possess components of motion that overlap considerably with the opponent direction, and rebound activity may shift the direction signaled by the MT macrocolumn.

Simulations of the model

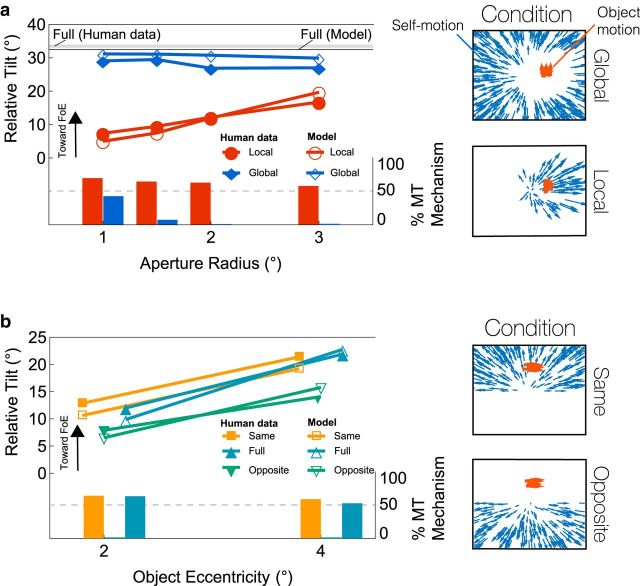
To assess the relative influence of the two mechanisms in recovering world-relative object motion, we compared the directional discrepancies between the retinal object motion and the MT signal (“tilt”) produced by model simulations to human judgments of object direction (Warren and Rushton, 2009). In their experiments, Warren and Rushton (2009) found that subjects judged a probe as moving toward the FoE when indeed it moved perpendicular (within 90 ± 15°) to the surrounding radial pattern of simulated self-motion (Fig. 1). The judged trajectory is consistent with the perception of the object's motion in a world-relative reference frame. Warren and Rushton (2009) concluded that the recovery of the object motion relies on a global process because removing large portions of the background flow surrounding the object only weakly affected object tilt judgments. However, a global process cannot fully account for the results because judgments exhibited bias toward the world-relative trajectory, even when the extent of background radial flow surrounding the object was small (see “Local” condition, Fig. 4a).

Figure 4.

a, Model simulations of Global and Local conditions of Warren and Rushton (2009). The Global condition contains a vertically moving object (red) and surrounding radial motion (blue) occluded by apertures of different sizes. The Local display is the inverse: surrounding radial motion is progressively revealed. Bottom, “% MT mechanism” bars represent the proportion of the tilt attributed to opponent direction disinhibition in MT. MSTd/MT feedback accounts for the remaining proportion. b, Model simulations of Same and Opposite hemifield conditions and Full condition of Warren and Rushton (2009). The object moves at two different eccentricities either on the same or opposite hemifield as the background motion.

We used the “Global” and “Local” displays from Warren and Rushton (2009) to investigate the contribution of MSTd/MT feedback. When the display contained the entire global motion pattern (“Full” condition), the relative tilt in the model estimate closely matched that of the human data (Fig. 4a, solid black and gray lines). Interactions within MT accounted for ∼45% of this effect, with the remaining portion attributed to feedback. Like humans, the model was only weakly affected (from 30° to 33° tilt) by the removal of the motion surrounding the object (Global condition, blue markers). Feedback dominated in the global condition, accounting for 60%–100% of the tilt effect (Fig. 4a, blue bars). In the Local condition (red markers), the overall tilt effect was weaker in both humans and the model, but the amount of surrounding radial motion around the object greatly influenced the tilt. Disinhibition played a much greater role, accounting for as much as 70% of the tilt, when the global motion pattern was absent. The limited global motion weakly engaged MSTd and led to only a small influence on MT through feedback.

Next, we used the “Same” and “Opposite” hemifield displays to further assess the contribution of disinhibition in MT. Similar to human judgments, the model tilt was greater when the object moved in the same hemifield as the background radial motion (Fig. 4b). This occurred because MT disinhibition contributed to the tilt in the “Same” (58%–63%), but not in the “Opposite” (0%) displays. Also consistent with human judgments, more eccentrically positioned objects produced a larger tilt. Feedback underlies the eccentricity effect in the model because the weight of feedback to MT units is hypothesized to increase the further their RF lies relative to the center of the MSTd unit's template (e.g., Fig. 2c, right). The hemifield was enough to strongly activate the MSTd cell tuned to the central heading, which resulted in a close correspondence in the model tilt garnered for the “Same” and “Full” displays.

Although Warren and Rushton (2009) investigated perceived tilt for objects that move perpendicularly with respect to the background flow, it is also important to consider human and model estimates for a wider range of trajectories. We simulated the model to generate predictions in the “Full” condition when the object moved along various trajectories relative to the neighboring background flow. Figure 5a reveals a symmetric pattern in the predicted tilt for objects that move toward (0°-180°) or away (180°-360°) the FoE. The tilt is greatest for the trajectories used by Warren and Rushton (2009) (90°/270°) and least when the object moves parallel to the background (0°/180°). The relative contribution of model mechanisms followed a similar tendency: MSTd feedback accounted for most of the tilt at the 90°/270° angles (70%) and the least for directions neighboring 180° (27%).

To compare the model object direction predictions with human judgments from similar conditions (Niehorster, 2013), we calculated a “flow parsing gain” measure (see Model estimate of flow parsing gain). A gain of 100% indicates that the visual system fully factors out the self-motion of the observer and recovers with world-relative motion of the object, and 0% indicates perception of object motion in the observer's reference frame. Figure 5b shows that overall the complete model with both mechanisms captures the human data well, although the model without interactions within MT provides a slightly better match in the perpendicular case.

Discussion

World-relative object motion signals in MT

A rather strong prediction that derives from our model is that MT cells come to signal an object's world-relative motion direction: surrounding a moving object with an optic flow pattern generated by self-motion should change the directional responses of MT neurons to the object compared with when it appears alone. For this to occur, MT cells must receive information about the observer's self-motion. The limited size of RFs does not make MT cells well suited to themselves extract information about the observer's self-motion, which depends on the global flow field. If MT cells signal world-relative object motion, information about self-motion likely propagates by feedback from an area sensitive to motion that encompasses most of the visual field. We suggest the feedback signals may originate from MSTd on the basis that MSTd neurons respond to the direction and speed of self-motion (Duffy and Wurtz, 1991, 1997) and the two areas are extensively interconnected (Boussaoud et al., 1990).

Because the recovery of world-relative object motion relies on information from outside the classical RF, the response may develop over time and deviate from initial velocity signals. The problem bears similarity to the aperture problem whereby local motion detectors can only signal components of motion perpendicular to a moving object's contour. While MT neurons initially signal the perpendicular component of motion, responses shift toward the veridical direction of the object after ∼60 ms (Pack and Born, 2001). Recovering world-relative object motion may similarly involve a dynamical solution: initial MT responses may reflect the reference frame of the observer and gradually converge onto the world-relative motion. Many MT neurons exhibit selectivity to the movement of an object in depth and the directional tuning may differ considerably to motion in a frontoparallel plane (Czuba et al., 2014). Given how frequently object motion must be perceived during self-motion, if these MT cells do indeed signal the 3D direction of object motion, then self-motion signals may modulate responses as indicated by our model.

Because units in MSTd integrate the temporally evolving motion signals in MT, object motion may influence the response of individual MSTd cells in the model, which is consistent with findings from Sasaki et al. (2013). However, the influence is modest for the objects considered here that occupy a small portion of the visual field. Objects that occupy larger areas may exert a larger influence and may even shift the most active cells in MSTd, consistent with biases in human heading perception (Layton and Fajen, 2016a, 2016b).

Model mechanisms in a broader context

Although the model transforms object motion into a world-relative reference frame in a manner that is consistent with human judgments, its parsimony excludes characteristics of MT and MSTd neurons that may play a role in object motion perception. MSTd neurons exhibit tuning to full-field radial expansion/contraction, spirals, rotation, and translation patterns (Graziano et al., 1994), which may reflect a sensitivity to the broad and complex range of motion encountered during ordinary self-motion. Including these more diverse populations of MSTd neurons within the MSTd-MT feedback mechanism could allow the model to capture world-relative motion perception under a variety of different types of self-motion.

MT neurons also exhibit considerable diversity in their RF organization, which extends beyond the type of cell included within the model that integrates motion throughout the RF (Cui et al., 2013). Many RFs contain not only a region that stimulates the neuron when motion in the preferred direction appears, but regions wherein motion suppresses the response (Allman et al., 1985b; Born and Tootell, 1992; Born, 2000). MT neurons with these antagonistic RF may play an important role in detecting the presence of an object that moves differently from the background and may therefore contribute in world-relative object motion perception.

MT neurons with antagonistic RFs appear to project to the lateral portion of ventral MST (MSTv) (Berezovskii and Born, 2000), which represents another area that may contain neurons that signal world-relative object motion. Limited evidence indicates that MSTv neurons respond to the movement of small moving targets (Tanaka et al., 1993), particularly when they appear at a different disparity than the background (Komatsu and Wurtz, 1988), but it is unclear whether these neurons are connected to MSTd or if self-motion signals other than those generated by eye or head movements affect responses to moving objects (Ilg et al., 2004). MSTv neurons may also play a role in perceiving the direction of a moving object during pursuit eye movements, when the eye movements completely null the retinal motion of the object (Komatsu and Wurtz, 1988).

Opponent direction disinhibition in MT

A number of studies (Mikami et al., 1986; Qian and Andersen, 1994; Heeger et al., 1999; Cui et al., 2013) support the existence of the type of inhibitory interactions among MT cells tuned to opponent motion directions proposed by our model. A key consequence of these interactions is rebound activation, an effect that has been shown to occur when opponent motion in an MT cell's inhibitory surround ceases (Allman et al., 1985a). The effects of motion in the inhibitory surround is delayed by ∼40 ms compared with when the MT cell is only activated in its excitatory center, which is compatible using horizontal connections that would be required for neurons tuned to opponent motion directions to interact within a macrocolumn.

If opponent inhibition plays an important role in world-relative object motion perception, our model makes several additional predictions about MT responses. First, among the MT cells that respond to a moving object passing in front of its background, those with RFs centered at the leading edge should demonstrate the greatest directional modulation. This is expected because, when the leading edge enters the RF, the cell integrates the rapid change between the background and object motion, which would generate the largest rebound effect. Second, although inhibitory interactions within the proposed model only occur locally within an MT macrocolumn, the spatial influence of the opponent-direction mechanism should be greater than we report. Our Global simulations show a rapid drop-off in MT mechanism contributions with increasing aperture sizes surrounding the object, but the mechanism should act over a larger spatial extent when the size of MT RFs is taken into account.

In conclusion, the proposed model extends beyond the flow parsing hypothesis by clarifying plausible mechanisms within the visual system involved in recovering the world-relative motion of objects during self-motion and quantifying the relative contributions between mechanisms that act globally and locally. The signals generated by MT neurons may provide crucial insight into the transformation performed by the visual system from observer-relative to world-relative references frames. Looking ahead, it is important to emphasize that object motion perception is a multisensory process, whereby nonvisual (e.g., vestibular, proprioceptive) self-motion information plays an important role (Fajen and Matthis, 2013; Fajen et al., 2013; Dokka et al., 2015). Future work will focus on adapting the model to accommodate multisensory self-motion information.