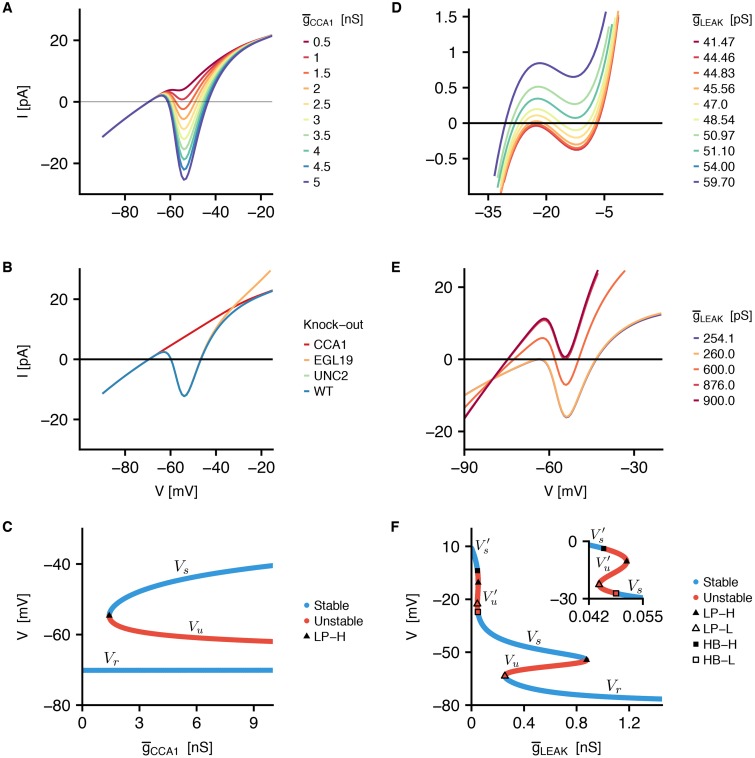
Fig 10. Analysis of the bistable behavior of RMD neuron.

A) Steady-state I-V curves at varying ${\overline{\mathbf{g}}}_{\text{CCA}1}$. Steady-state I-V curves are obtained from the currents computed during a voltage clamp stimulation with steps ranging between -90 mV and -10 mV, with 1 mV increments. The value of ${\overline{g}}_{\text{CCA}1}$ is varied between 0.5 nS and 5 nS with 0.5 nS increments. B) Calcium channels knockouts steady-state I-V curves. Voltage clamp simulation follows the same protocol of panel A. Knockout I-V curves are computed by removing the contribution of one of the CaV from the total current, leaving unchanged the other conductances. C) Bifurcation diagram with ${\overline{\mathbf{g}}}_{\text{CCA}1}$ as bifurcation parameter. The black empty triangle represents the saddle-node (or limit point LP-H) bifurcation point [V, ${\overline{g}}_{\text{CCA}1}$] = [-59.5 mV, 1.14 nS]. At ${\overline{g}}_{\text{CCA}1}>1.14\text{nS}$ the system exhibits three fixed points: two stable (V_r and V_s) and one unstable (V_u). D)-E) Steady-state I-V curves for different values of ${\overline{\mathbf{g}}}_{\text{LEAK}}$. The passive conductance is varied between 0.04 nS and 0.9 nS to obtain the steady-state I-V curve in correspondence of the different regimes highlighted also by the bifurcation diagram analysis (panel F). The applied voltage stimuli ranges from -90 mV to -30 mV with 0.8 mV increments, in panel D, and from -35 mV to +5 mV with 0.8 mV increments, in panel E. Step duration 1300 ms, holding potential V_h = −70 mV. F) Bifurcation diagram with ${\overline{g}}_{\text{LEAK}}$ as bifurcation parameter. For 0.25 nS $<{\overline{g}}_{\text{LEAK}}<0.9\text{nS}$ two stable solutions are separated by an unstable one. These correspond to V_r, V_s and V_s in panel C. At lower values of ${\overline{g}}_{\text{LEAK}}$, and by decreasing the parameter, two unstable solutions $V_u^{\prime }$ and $V_s^{\prime }$ arise from a LP bifurcation (LP-H), with $V_s\le V_u^{\prime }\le V_s^{\prime }$. By decreasing the control parameter, $V_s^{\prime }$ gains stability through a subcritical Hopf bifurcation (HB-H), while at lower values of the control parameter, V_s loses stability through a second subcritical Hopf bifurcation (HB-L). Finally, by further lowering the parameter, $V_u^{\prime }$ and V_s collide in a second fold bifurcation (LP-L) and $V_s^{\prime }$ remains the only stable solution at even lower values of ${\overline{g}}_{\text{LEAK}}$. A second bistable regime may occur in between the two Hopf bifurcations.