Magnetic Characterization of Iron Oxide Nanoparticles for Biomedical Applications

Abstract

Iron oxide nanoparticles are of interest in a wide range of biomedical applications due to their response to applied magnetic fields and their unique magnetic properties. Magnetization measurements in constant and time-varying magnetic field are often carried out to quantify key properties of iron oxide nanoparticles. This chapter describes the importance of thorough magnetic characterization of iron oxide nanoparticles intended for use in biomedical applications. A basic introduction to relevant magnetic properties of iron oxide nanoparticles is given, followed by protocols and conditions used for measurement of magnetic properties, along with examples of data obtained from each measurement, and methods of data analysis.

1. Introduction

Iron oxide magnetic nanoparticles have been widely used due to the capability of manipulating particle motion, causing energy dissipation, or providing imaging contrast in the presence of an external magnetic field [1, 2]. Their use in biomedical applications such as cancer therapy [3, 4], magnetically triggered drug release [5, 6], magnetofection [7, 8], magnetic resonance imaging [9, 10], and magnetic particle imaging [11, 12] has been widely researched. Examples of important magnetic properties of nanoparticles include the saturation magnetization, remanence and coercivity, magnetic diameter, magnetocrystalline anisotropy constant, mechanism of magnetic relaxation, and blocking temperature, all of which can be material specific and may be influenced by the method of synthesizing and coating the nanoparticles and by the method of sample preparation for magnetic measurements. Accurately quantifying these properties is vital to enable reproducibility in research and to achieve the maximum potential of iron oxide nanoparticles in specific applications. Unfortunately, many publications describing the preparation and use of magnetic nanoparticles lack even basic magnetic characterization, making it difficult to evaluate and compare the work. The methods described in this chapter present detailed procedures to determine the magnetic properties of iron oxide nanoparticles that most significantly impact their biomedical applications.

The magnetic response of iron oxide nanoparticles to an external field depends mainly on the degree of magnetic ordering and on the temperature of the sample. The magnetic moment per unit volume of particle, i.e., the magnetization, may be defined depending on the spin or the orbital energy possessed by the dipole. Particles with large crystallite sizes have dipoles arranged in multiple domains separated by a domain wall so as to maintain the lowest energy state. There exists a critical size (typically less than 100 nm) below which it is energetically unfavorable for domain walls to form, resulting in single domain nanoparticles [13]. As predicted by Louis Néel, nanoparticles in the single domain regime no longer exhibit hysteresis behavior in an applied magnetic field, a condition that is referred to as superparamagnetism [14]. The most commonly used magnetic nanoparticles are ferrites MFe₂O₄ that exhibit a spinel or inverse spinel structure. The distribution of the metal ions relative to the oxygen ions in the crystal lattice results in the formation of dipoles and determines the overall magnetization of the material. A measure of this ordering and the strength of the dipoles in single domain particles may be obtained from the magnetic diameter obtained from fitting the Langevin equation (see Subheading 3.5) to an experimental equilibrium magnetization curve [15, 16].

In the presence of a magnetic field, magnetic spins tend to align in the direction of the field, resulting in an induced magnetization [17]. The maximum induced magnetization is termed the saturation magnetization of the sample. This induced magnetization may remain even after the field is removed, in which case it is referred to as the remanent magnetization. In those cases, the coercive field corresponds to the magnetic field required to revert the magnetization to zero. Nanoparticles with ferro- and ferri-magnetic behavior often exhibit hysteresis. In nanoparticles that exhibit superparamagnetism, remanence and coercive field becomes negligible.

Nanoparticles show a certain preference for the direction along which their magnetic dipole tends to align, referred to as magnetic anisotropy, which can arise due to the shape and inherent crystalline structure of the nanoparticles. This anisotropy can be intrinsic to the material such as magnetocrystalline, shape, and exchange anisotropy, or induced by an external process. Magnetocrystalline anisotropy refers to the tendency of the magnetization to align along a preferred crystallographic direction. In contrast, polycrystalline samples with no preferred crystal orientation tend to magnetize along a long axis, in what is known as shape anisotropy. Finally, exchange anisotropy arises from interaction between antiferromagnetic and ferromagnetic materials [13, 17]. The rate at which the magnetic dipole within a particle will align in a given direction of applied magnetic field is influenced by the temperature of the system (thermal energy) and the magnitude of the magnetic anisotropy energy barrier between easy axes for magnetization.

The magnitude of the magnetocrystalline anisotropy can be determined by temperature-dependent magnetization measurements such as zero-field-cooled (ZFC) and Dynamic Magnetic Susceptibility (DMS) curves in samples wherein nanoparticles’ physical rotation is suppressed, either by freezing the sample or dispersing it in a solid matrix (see Subheadings 3.7 and 3.8).

There are two mechanisms by which the magnetization of a colloidal suspension of nanoparticles responds after the removal of an external applied field [18–20]. In the first mechanism, the relaxation of the magnetic dipole occurs by physical particle rotation in the liquid. The corresponding characteristic rotational diffusion time τ_B, referred to as the Brownian relaxation time, is given by

$${\tau }_{\text{B}}=\frac{3V_{\text{h}}\eta }{kT}$$ (1)

where η is the viscosity of the carrier liquid, V_h is the hydrodynamic volume of the particle, k is the Boltzmann constant, and T is the temperature. In the second mechanism, the magnetic dipole rotates within the particle. The corresponding characteristic time τ_N for dipole rotation is termed the Néel relaxation time and is given by

$${\tau }_{\text{N}}={\tau }_0\exp \left(\frac{K{V}_{\text{m}}}{kT}\right)$$ (2)

where τ₀ is a characteristic time with an approximate value of 10⁻⁹s, V_m is the magnetic core volume, and K is the anisotropy constant. In a colloidal suspension of nanoparticles, both relaxation mechanisms are present but the faster mechanism dominates. The Brownian relaxation time is proportional to the viscosity of the carrier liquid and the particle hydrodynamic diameter, whereas the Néel mechanism is solely related to the volume of the magnetic core and the anisotropy constant of the material. Dynamic Magnetic Susceptibility (DMS) measurements (see Subheadings 3.9) can be used to obtain information of the magnetic relaxation properties of nanoparticles in suspension, including measurements of their characteristic magnetic relaxation time.

Here, we describe in detail how superconducting quantum interference device (SQUID) magnetometers and dynamic magnetic susceptometers can be applied to quantify magnetic properties of iron oxide nanoparticles in a liquid or solid matrix. Sample preparation methods and data analysis are also explained. We remark that determining properties of nanomaterials is often difficult on the basis of a single technique. The methods described in this chapter should provide a fairly complete assessment of the magnetic properties of iron oxide nanoparticles that most significantly impact their biomedical applications including low and high field magnetization curves, Zero-Field-Cooled/Field-Cooled (ZFC/FC) magnetization curves, and Dynamic Magnetic Susceptibility (DMS) measurements. However, there are other magnetic measurements, such as isothermal reversibility measurements, First Order Reversal Curves (FORC), and Verwey transition analysis that we have left out of this chapter [21–25]. The reader may adapt this protocol to characterize their specific nanoparticle of interest by taking into consideration the compatibility of the particle surface coating with the polymer or solvent selected.

2. Materials

2.1. Immobilization of Hydrophobic Nanoparticles in a Solid Matrix (See Note 1)

1. Magnetic nanoparticles synthesized or obtained commercially and coated with organic molecules such as oleic acid, hydrophobic polymers, and oleylamine.

2. Styrene ReagentPlus®, containing 4-tert-butylcatechol as a stabilizer, ≥99%. Store at 4 °C.

3. Divinylbenzene technical grade, 80% (DVB). Store at 4 °C.

4. 2,2′-Azobis(2-methylpropionitrile) (AIBN). Store at 4 °C.

5. 3 mL glass vial.

6. 0.7 mL glass test tubes with screw cap (6 mm OD, 50 mm length).

7. Ultrasonicator probe fitted with a tapered microtip (3/6 in).

8. Oil bath.

2.2. Immobilization of Hydrophilic Nanoparticles in a Solid Matrix (See Note 2)

1. Magnetic nanoparticles synthesized or obtained commercially and coated with hydrophilic molecules, such as hydrophilic polymers, amines, carboxylic groups or peptized.

2. Tetraethylene glycol dimethacrylate (TEGDMA), technical grade, ≥90%. Store at 4 °C.

3. 2,2′-Azobis(2-methylpropionitrile) (AIBN). Store at 4 °C.

4. 3 mL glass vial.

5. 0.7 mL glass test tubes with screw cap (6 mm OD, 50 mm length).

6. Ultrasonicator probe fitted with a tapered microtip (3/6 in).

7. Oil bath.

2.3. Nanoparticle Suspensions

1. Magnetic nanoparticles: Iron oxide, cobalt ferrite, manganese ferrite, etc., synthesized or obtained commercially. This protocol uses iron oxide nanoparticles.

2. Toluene, hexane, chloroform, 1-octadecene, tetrahydrofuran, or any organic solvent suitable to suspend particles coated with organic molecules, such as oleic acid or oleylamine. This protocol uses iron oxide nanoparticles coated with oleic acid suspended in 1-octadecene.

3. Water or other suitable polar solvents to suspend particles coated with hydrophilic molecules, such as hydrophilic polymer, amines, carboxylic groups, or peptized. This protocol uses water.

4. Filters: Nylon filters for filtration of aqueous solutions. Polytetrafluoroethylene (PTFE) filters for filtration of organic solvents. Polyvinylidene fluoride (PVDF) filters for filtration of nonaggressive aqueous and mild organic solutions (see Note 3).

5. Mechanical ultrasonic bath.

2.4. Equipment

1. Dynamic magnetic susceptometers operating at low amplitude fields ~0.5 mT with an ideal excitation frequency ranging from 1 to 100 kHz (such as Acreo DynoMag).

2. Vibrating sample magnetometer (VSM) (such as 7400-S from Lake shore Cryotronics, or VSM from Quantum Design).

3. Superconducting Quantum Interference Device (SQUID) magnetometer (such as MPMS3 from Quantum Design or S700X from Cryogenic Ltd) (see Note 4).

3. Methods: Sample Preparation

As seen in the introduction, magnetic nanoparticles may relax by either of two mechanisms; Néel and Brownian relaxation. Distinguishing between these two mechanisms of magnetic relaxation is critical in many biomedical applications, as physical particle rotation may be significantly impaired once nanoparticles accumulate in tissues or inside cells. Measuring magnetic properties for nanoparticles fixed in a solid matrix allows one to abrogate the effects of Brownian relaxation in the magnetic response of the nanoparticles during a measurement, whereas when the nanoparticles are in suspension both mechanisms contribute to the response. As such, characterization of samples in liquid and solid matrices can provide useful insights into their relaxation-dependent properties.

3.1. Immobilization of Hydrophobic Nanoparticles in a Solid Matrix

1. Prepare a stock solution of the monomers and initiator by mixing 3 mL of styrene, 450 μL of DVB, and 10 mg of AIBN in a 10 mL glass vial (see Note 5).

2. Weigh ~10 mg of the magnetic nanoparticle sample into a glass vial. The weight percentage of the magnetic core in the sample must be measured prior to immobilization in a solid matrix, so as to properly estimate the amounts for the various components (see Note 6).

3. Add appropriate amount of the monomer/initiator solution to the nanoparticles in the glass vial to obtain a concentration of magnetic core of ~0.1 wt% (see Note 7). For example, if the nanoparticle sample (i.e., magnetic core and the ligands on the particles) is 15 wt% of magnetic core and 85 wt% ligands on the particle, add 1.5 g of the monomer/initiator solution (1.5 mL assuming density ~1 g/mL) to 0.01 g of magnetic nanoparticle sample, such as the final magnetic core concentration in the solution is 0.1 wt%.

4. Shake the solution vigorously. If necessary, use an ultrasonicator probe fitted with a tapered microtip (3/16 in.) to disperse the particles in the polymer.

5. Place 500 μL of the solution in glass test tubes with screw-cap (Fig. 1).

6. Place the tube in an oil bath and increase the temperature to 70 °C.

7. Allow the reaction to proceed for 4 h. The monomer should be completely polymerized, forming a solid matrix (Fig. 1).

8. To release the polymer from the tube, tap the sides of the tube. Do this lightly and be careful not to break the sample or the glass tube.

9. Weigh the sample to account for any evaporation losses and recalculate the nanoparticle concentration if needed.

Fig. 1.

Sample preparation. (a) 500 μL of the mixture iron oxide nanoparticles and poly(styrene-divinylbenzene) in glass test tubes. (b) Iron oxide nanoparticles immobilized in a poly(styrene-divinylbenzene). (c) Iron oxide nanoparticles in water solution

3.2. Immobilization of Hydrophilic Nanoparticles in a Solid Matrix

1. Weigh ~10 mg of the magnetic nanoparticle sample into a glass vial. The weight percentage of the magnetic core in the sample must be measured prior to immobilization in a solid matrix, so as to properly estimate the amounts for the various components (see Note 6).

2. Add the appropriate amount of the tetraethylene glycol dimethacrylate (TEGDMA) to obtain a concentration of magnetic core of ~0.1 wt% (see Note 7). For example, to embed 0.01 g of magnetic nanoparticles with a 10 wt% of magnetic core (i.e., 10 wt% magnetic core and 90 wt% polymer coating), add 1.0 g of the monomer/initiator solution (1.0 mL assuming density ~1 g/mL), such as the final magnetic core concentration in the solution is 0.1 wt%.

3. Shake the solution vigorously. If necessary, use an ultrasonicator probe fitted with a tapered microtip (3/16 in.) to disperse the particles in the polymer.

4. Add AIBN to the previous solution to a concentration of 0.04 wt%.

5. Place 500 μL of the solution in glass test tubes with screw-cap.

6. Place the tube in an oil bath and increase the temperature to 70 °C.

7. Allow the reaction to proceed for 4 h. The monomer should polymerize, forming a solid matrix.

8. To release the polymer from the tube, tap the sides of the tube. Do this lightly and be careful not to break the sample or the glass tube.

9. Weigh the sample to account for any evaporation losses and recalculate particle concentration if needed.

3.3. Suspending Nanoparticles in a Liquid Matrix

1. Weigh ~ 10 mg of the magnetic nanoparticle sample. The weight percentage of the magnetic core in the sample must be measured prior to suspension in a liquid matrix, so as to properly estimate the amounts for the various components (see Note 6).

2. Add the approximate amount of solvent (organic for hydrophobic nanoparticles, water for hydrophilic nanoparticles) to obtain a concentration of magnetic cores of ~0.1 wt% (Fig. 1c, see Note 7).

3. Use a sonic bath to suspend the particles in the solvent.

4. Filter the solution using a syringe filter.

3.4. Methods: Magnetic Measurements and Data Analysis

For demonstration purposes this chapter describes the use of a solid sample prepared with oleic acid coated iron oxide nanoparticles embedded in a poly(styrene-divinyl benzene) matrix (PSDVB), which inhibits particle rotation, and nanoparticles suspended in 1-oactadecene to allow for nanoparticle rotation. The reader may adapt this protocol to characterize their specific nanoparticle of interest by taking into consideration the compatibility of the particle surface with the polymer or solvent selected.

In the following protocol, a Quantum Design MPMS3 Superconducting Quantum Interference Device (SQUID) magnetometer is used in Subheadings 3.5–3.8 to determine the saturation magnetization, remanence and coercivity, magnetic diameter, magnetocrystalline anisotropy constant, and blocking temperature solid samples. An Acreo DynoMag dynamic magnetic susceptometer is used in Subheading 3.9 to estimate the mechanism of magnetic relaxation of the nanoparticles in a liquid matrix. The reader is assumed to be familiar with the equipment and relevant software described associated with these instruments, or the instruments chosen to carry out similar characterization experiments.

3.5. Magnetization Vs. Magnetic Field (MH) at Constant Temperature

The MH curve allows one to verify the superparamagnetic behavior of the nanoparticles and determine their saturation magnetization. Furthermore, a superparamagnetic MH curve can be analyzed by fitting to the Langevin function and a lognormal size distribution to estimate the magnetic diameter of the nanoparticles [15, 16]. Finally, in cases where the nanoparticles are not superparamagnetic, the equilibrium magnetization curve can be used to determine the remanence and coercivity of the nanoparticles at a given temperature. It should be noted that to properly verify superparamagnetic behavior in a sample the nanoparticles should be prevented from rotating. This is because a collection of ferro/ferrimagnetic nanoparticles in liquid suspension will be able to physically rotate to align their magnetic dipoles in the direction of the magnetic field, resulting in an MH curve that lacks remanence and coercivity. This situation is called extrinsic supaerparamagnetism, whereas the case when the nanoparticles are fixed in a matrix and their MH curve lacks remanence and coercivity and follows the sigmoid function (typical S-shape) is called intrinsic superparamagnetism [16]. This is not to say that MH curves should not be obtained for liquid samples, as such measurements can still yield the magnetic diameter of the nanoparticles and can also be used to estimate the volume fraction of nanoparticles in the suspension. In a typical measurement, the magnetization (magnetic moment per unit of volume) of a sample is measured as a function of the applied magnetic field at constant temperature. The magnetic diameter distribution, saturation magnetization, coercive field and remanent magnetization can all be determined from MH curves.

1. Fix the magnetic nanoparticles in a solid matrix as explained in Subheadings 3.1 and 3.2. In this protocol we use iron oxide nanoparticles in a PSDVB matrix. The reader may adapt this protocol to use a polymer or solid matrix compatible with their nanoparticle system (see Notes 1 and 2).

2. Set the desired sample temperature using the equipment software (see Note 8). We use a Superconducting Quantum Interference Device (SQUID) magnetometer MPMS3 from Quantum Design. The reader is assumed to be familiar with the equipment and relevant software described in Subheading 2.4.

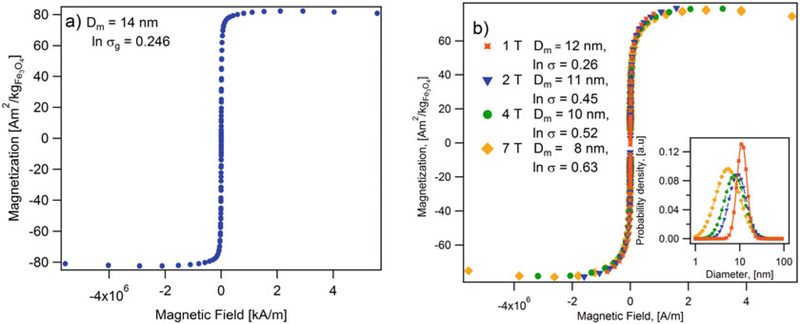
3. Measure the magnetization M(H) of the sample with increasing magnetic field. Use of an applied magnetic field range of 7 to −7 T with a field ramp of 200 Oe/min is highly recommended (see Note 9). In Fig. 2a, the magnetization curve of iron nanoparticles is measured at different saturation fields.

4. The magnetic diameter and its distribution is a measure of the strength of the magnetic dipole within each nanoparticle. The volume median magnetic diameter (D_m) and geometric deviation (lnσ_g) can be found by fitting the superparamagnetic equilibrium magnetization curve to the Langevin function, weighed using a lognormal size distribution n_v(D_m) (see Eq. (5)), as suggested by Chantrel et al. [15, 16].

   $$M(\alpha )=M_{\text{s}}{\int }_0^{\infty }{n}_{\text{v}}\left(D_{\text{m}}\right)L(\alpha )d{D}_{\text{m}}$$ (3)

   $$L(\alpha )=\coth (\alpha )-\frac{1}{\alpha };\text{where}\alpha =\frac{\pi {\mu }_0{D}_{\text{m}}^3{M}_{\text{d}}H}{6k_{\text{B}}T}$$ (4)

   $$n_{\text{v}}\left(D_{\text{m}}\right)=\frac{1}{\sqrt{2\pi }D\ln {\sigma }_{\text{g}}}\exp \left(\frac{\ln \left(D_{\text{m}}/D_{\text{pgv}}\right)}{2\left({\ln }^2{\sigma }_{\text{g}}\right)}\right)$$ (5)

   In Eq. (4), α is the Langevin parameter (ratio of magnetic to thermal energy), μ₀ is the permeability of free space, k_B is Boltzmann’s constant, and T is the absolute temperature, and M_d is the domain magnetization (446000 A/m or 86 Am²/kg for iron oxide).

5. See Fig. 2a for an example of a MH curve for iron oxide nanoparticles embedded in a PSDVB matrix at a concentration of $0.057{\text{mg}}_{{\text{Fe}}_3{\text{O}}_4}$. Using Eq. (3), the volume median magnetic diameter is D_m = 14 nm with lnσ_g = 0.246 at 300 K. The saturation magnetization is $\sim 83{\text{Am}}^2/{\text{kg}}_{{\text{Fe}}_3{\text{O}}_4}$, which is in the range of reported values for magnetite and maghemite (80 – 100Am²/kg) [26].

6. For the same sample, the magnetic diameter, calculated using the Langevin-Chantrel model [15, 16], decreases as the saturation field increases (see Fig. 2b). This is because measurements carried in low field strength would cause only larger particles to respond to the magnetic field and thus narrow size distribution is obtained. A true representation of the magnetic diameter and its distribution can be obtained only if the measurements are run at fields much greater than the fields that saturate the particles, such that even smaller particles respond at large magnetic field strengths.

Fig. 2.

(a) Magnetization curves of iron oxide nanoparticles in a poly(styrene-divinylbenzene) matrix measured at different saturation fields. Annotations indicate the magnetic diameter and the geometric deviation calculated using the Langevin-Chantrel model. Inset figure shows the magnetic diameter distribution. (b) Magnetization curve at 300 K for iron oxide nanoparticles in a poly(styrene-divinylbenzene) matrix. Annotations indicate the magnetic diameter (14 nm) and the geometric deviation (ln σ = 0.246)

3.6. Low Field Magnetization

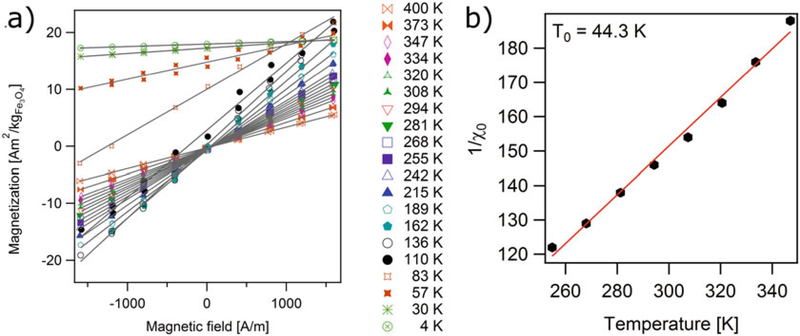
The extent of magnetic dipole-dipole interactions in a sample can be parameterized using the so-called interaction temperature parameter T₀. This parameter can be estimated from low field (± 10–40 Oe, depending on the sample) MH curves for the sample, measured at various temperatures in a wide temperature range. The sample needs to be solid or embedded in a matrix to restrict particle rotation during the measurement (see Subheading 3.1 or 3.2). Under such conditions, the MH curves will be linear for superparamagnetic samples and the slope of the curves, which corresponds to the initial susceptibility of the sample, will be sensitive to the dipole-dipole interactions. The inverse of the initial susceptibility can then be plotted as a function of temperature and fitted to a Curie-Weiss model to obtain T₀ [27]. We note that T₀ can be a function of the state of aggregation of the iron oxide nanoparticles in a sample, or of the extent of dipole-dipole interactions in concentrated samples.

1. Embed the magnetic nanoparticles in a solid matrix as explained in Subheadings 3.1 and 3.2. In this protocol, we use iron oxide nanoparticles in a PSDVB matrix. The reader may adapt this protocol to use a polymer or solid matrix compatible with their nanoparticle system (see Notes 1 and 2).

2. Set the desired sample temperature using the equipment software (see Note 8). We use a Superconducting Quantum Interference Device (SQUID) magnetometer MPMS3 from Quantum Design. The reader is assumed to be familiar with the equipment and relevant software described in Subheading 2.4.

3. Measure the magnetization of the sample as a function of increasing the applied magnetic field. Typically, the magnetization is measured for about ten magnetic field steps, uniformly distributed in the field range. The applied field may range from 0.004 to −0.004 T and a field ramp of 0.001 T/min is suitable.

4. Determine the initial susceptibility χ₀ of the sample at different temperatures by calculating the slope of the M(H) curve. Then plot 1/χ₀ versus T and fit to the Curie-Weiss model [28]

   $${\chi }_0=\frac{A}{(T-T_0)}.$$ (6)

   where the data is expected to lie in a straight line whose intercept with the 1/χ₀ axis corresponds to the interaction temperature parameter T₀.

5. Figure 3a shows representative low field magnetization curves for iron oxide nanoparticles in a PSDVB matrix in a temperature range of 4–400 K. Note that for temperatures of 136 K and higher the low field MH curves are linear and cross the origin, indicating superpamagnetic behavior. For temperatures below 136 K the low field MH curves still appear linear but no longer cross the origin, indicating the sample has significant remanence and coercivity and is therefore no longer superparamagnetic.

6. Figure 3b shows the linear relation between the inverse of the initial susceptibility and temperature for the sample. Typically, this linear relation only holds for a limited temperature range, which usually starts much higher than the temperature for which the sample becomes superparamagnetic. For the sample in Fig. 3b the range starts at about ~260 K, even though the sample appeared superpamagnetic at a temperature of 136 K in Fig. 3a. Using the model in Eq. (6), the interaction temperature parameter for this sample was determined to be T₀ = 43.2 K.

Fig. 3.

(a) Low field magnetization curves for iron oxide nanoparticles in a poly(styrene-divinylbenzene) matrix, at temperatures between 4 K and 400 K and (b) initial susceptibility data fitted to Curie-Weiss model

3.7. Zero-Field-Cooled/Field-Cooled (ZFC/FC) Magnetization Curves

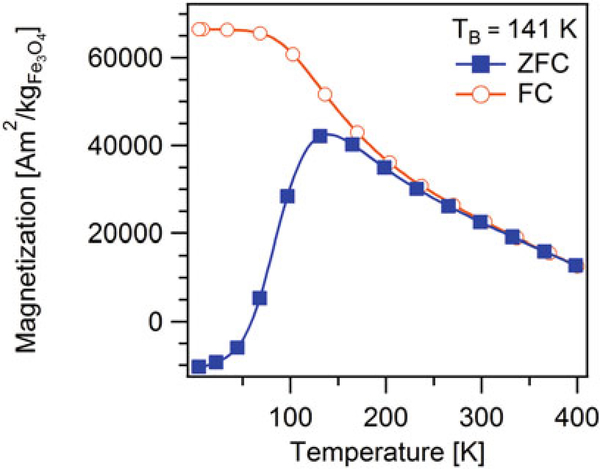
Whether a given collection of magnetic nanoparticles displays superparamagnetic or ferro/ferrimagnetic behavior depends on the temperature at which the measurement is made. This is because superparamagnetism corresponds to a state where the energy barrier to dipole moment rotation in the crystal is much smaller than the thermal energy. As such, the temperature at which a collection of magnetic nanoparticles transitions from ferro/ferrimagnetic behavior to superparamagnetic behavior is an important property. This can be characterized through temperature-dependent magnetization M(T) measurements. The most common way to do this is through so-called Zero-Field-Cooled and Field-Cooled (ZFC/FC) measurements. In such measurements a sample, usually solid or embedded in a solid matrix, begins at a high temperature and at zero field, such that thermal energy completely eliminates any magnetization in the sample. Then the sample is cooled to a low temperature in zero field. The ZFC portion of the plot is obtained by applying a magnetic field once the sample has equilibrated at the lowest temperature and then by measuring the sample’s magnetization with increasing temperature. At the lowest temperature the dipoles in the nanoparticles will have the lowest amount of thermal energy, and as such will only align slightly with the applied field, resulting in a small magnetization value. As the temperature increases, the increasing thermal energy of the magnetic dipoles will free them from their initial states, resulting in increased alignment with the field and increasing sample magnetization. However, beyond a certain temperature, referred to as the blocking temperature, further increasing thermal energy will lead to a decrease in the extent of alignment of the magnetic dipoles with the applied field and hence to a decrease in the sample magnetization. The FC portion of the curve is obtained by then measuring magnetization as the sample is cooled back in the applied field to the initial low temperature. In an ideal sample the ZFC and FC curves will overlap at temperatures above the blocking temperature and diverge at temperature below the blocking temperature. For samples with significant dipole-dipole interactions or broad size distributions there will be a significant temperature range above the blocking temperature where the ZFC and FC curves do not overlap. Also, the shape of the FC curve below the blocking temperature can also be indicative of the extent of dipole-dipole interactions in a sample. Finally, the blocking temperature can be analyzed to obtain an estimate of the anisotropy constant of the nanoparticles in the sample, by using equations that consider the Néel and Volger-Fulcher models for the magnetic relaxation time.

1. Embed the magnetic nanoparticles in a solid matrix as explained in Subheadings 3.1 and 3.2. In this protocol, we use iron oxide nanoparticles in a PSDVB matrix. The reader may adapt this protocol to use a polymer or solid matrix compatible with their nanoparticle system (see Notes 1 and 2).

2. Heat the sample to the highest working temperature in the absence of an applied magnetic field (see Note 10). Hold this condition for at least 5 min. We use a SQUID magnetometer MPMS3 from Quantum Design. The reader is assumed to be familiar with the equipment and relevant software described in Subheading 2.4.

3. Set the sample temperature to the lowest value, depending on the actual sample and instrument limit (see Note 11). For iron oxide nanoparticles, we usually start at 10 K. Use cooling rates of 5–10 K/min while cooling down.

4. At the lowest temperature, apply a small magnetic field (10–100 Oe, see Note 12).

5. 5. Measure the magnetization of the sample as the temperature increases from 10 to 400 K. Use a temperature sweep rate of 10 K/min and measure the magnetic moment at least every 2 K (see Note 13).

6. Decrease the temperature from 400 K to 10 K under a small magnetic field (10–100 Oe) and measure the magnetization at least every 2 K. We recommend using a temperature sweep rate of 10 K/min (see Note 13).

7. The temperature at which the ZFC magnetization curve exhibits a maximum is called the blocking temperature (T_B) (see Fig. 4). Many authors assume that at the blocking temperature the time scale of the measurements is comparable to the Néel relaxation time, given by Eq. (2) and therefore the anisotropy constant is determined by

   $$K=\frac{k_{\text{B}}\left(T_{\text{B}}\right)}{V_{\text{m}}}\ln \left(\frac{{\tau }_{\text{obs}}}{{\tau }_0}\right)$$ (7)

   where V_m is the magnetic volume, calculated using the magnetic diameter determined in Subheading 3.5, τ_obs is the observation time in seconds, T_B is the blocking temperature, τ₀ is the characteristic time, typically assumed to be ~10⁻⁹s. The observation time used to calculate anisotropy constant is the ratio between blocking temperature and rate set to reach the temperature, i.e., the sweep rate during measurement (10 K/min for the procedure described above).
8. Recognizing the influence of magnetic dipole-dipole interactions in the relaxation time of the nanoparticles, shtrikman and wolhlfarth [27] proposed the Vogel-Fulcher law, which can be used to estimate the anisotropy constant in samples with significant interactions

   $$K=\frac{k_{\text{B}}\left(T_{\text{B}}-T_0\right)}{V_{\text{m}}}\ln \left(\frac{{\tau }_{\text{obs}}}{{\tau }_0}\right)$$ (8)

   where T₀ is the interaction temperature parameter. To estimate the anisotropy constant, one requires independent knowledge of T₀, τ₀, and τ_obs.
9. Polydispersity of the sample may be accounted for in Eqs. (7) and (8) by calculating K according to

   $$K=\frac{k_{\text{B}}\left(T_{\text{B}}-T_0\right)}{V_{\text{m}}}\ln \left(\frac{{\tau }_{\text{obs}}}{{\tau }_0}\right)\frac{1}{\exp \left(9/2{\ln }^2{\sigma }_{\text{g}}\right)}$$ (9)

10. Figure 4 shows a representative ZFC-FC magnetization curve for the same sample used in Subheading 3.5. The blocking temperature was T_B = 137 K, which is similar to the temperature for which the low field MH curves became linear and crossed the origin in Fig. 3a. Furthermore, note that the ZFC and FC curves do not overlap until temperatures above ~260 K. This is evidence of significant dipole-dipole interactions in the sample and also explains in part why the linear relationship between inverse initial susceptibility and temperature was observed at temperatures above ~260 K in Fig. 3b.

    The calculated values of the anisotropy constant K using the maximum temperature of the ZFC curve, and the Néel or Vogel-Fulcher models for the relaxation time are summarized in Table 1. Because the Vogel-Fulcher model takes into account the particle-particle interaction parameter T₀, the value obtained using the Néel model is larger than that calculated using the Vogel-Fulcher model. However, both values are slightly larger than the magnetocrystalline anisotropy constant of bulk magnetite 13.5 kJ/m³ [29]. When the polydispersity of the magnetic diameter is included in the analysis, the calculated values decrease and are comparable to the bulk value.

Fig. 4.

Zero field cooled (closed symbols) and field cooled (open symbols) magnetization curve for iron oxide nanoparticles in a poly(styrene-divinylbenzene) matrix, obtained at temperatures between 4 and 400 K using a 796 A/m (10 Oe) field

Table 1.

Anistropy constant for Iron Oxide nanoparticles (D_m = 14 nm ) in a PSDVB matrix. Results from ZFC and DMS measurements

		Néel model		Vogel-Fulcher model
		Inσg = 0	Inσg = 0.246	Inσg = 0	Inσg = 0.246
ZFC	KZFC [KJ/m3]	46.59	35.48	27.90	21.25
DMS susceptibility	τ0 [s]	3.18 × 10−19	3.18 × 10−19	1.09 × 10−14	1.09 × 10−14
	KDMS [KJ/m3]	61.15	46.58	32.28	24.59

3.8. Dynamic Magnetic Susceptibility (DMS) as a Function of Temperature

The transition from ferro/ferrimagnetic behavior to superparamagnetic behavior can also be determined from measurements of the dynamic magnetization of the nanoparticles in response to an oscillating magnetic field as a function of temperature. The measurements are usually done in solid samples or samples in a solid matrix to inhibit the particle rotation (see Subheadings 3.1 and 3.2).

In these measurements, the so-called complex or dynamic magnetic susceptibility $\widehat{\chi }(T)={\chi }^{\prime }-i{\chi }^{\prime \prime }$ of the nanoparticles is determined as a function of temperature for various applied oscillating field frequencies. Here, χ′ is referred to as the in-phase susceptibility and χ″ is referred to as the out-of-phase susceptibility. This approach poses several advantages over ZFC/FC measurements to determine the anisotropy constant of the nanoparticles. First, the measurements are done in the absence of an applied constant field and the oscillating excitation field is of small magnitude, such that the Néel and Vogel-Fulcher models for the magnetic relaxation time are expected to be good descriptions of the behavior of the nanoparticles. Second, the observation time is precisely determined by the inverse of the frequency of the applied oscillating magnetic field and can be easily varied by changing the applied oscillating field frequency. This in turn allows one to determine the anisotropy constant without having to assume a value for τ₀.

1. Fix the magnetic nanoparticles in a solid matrix as explained in Subheadings 3.1 and 3.2.

2. Heat the sample to the highest working temperature in the absence of an applied magnetic field (see Note 10). Hold this condition for at least 5 min. We use a SQUID magnetometer MPMS3 from Quantum Design in this protocol. The reader is assumed to be familiar with the equipment and relevant software described in Subheading 2.4.

3. Set the amplitude of the field in the range of 2–5 Oe.

4. Set the desired frequency of oscillation of the AC field. The same measurement must be repeated at multiple frequencies. The selected frequencies should be in a range that spans several orders of magnitude (0.1–1000 Hz).

5. Measure the in-phase and out-of-phase components of the magnetic susceptibility of the sample under a constant amplitude oscillating field as the temperature is decreased from 400 to 4 K. During the measurement, start with the highest temperature and decrease temperature at a rate of 6 K/min (see Note 14).

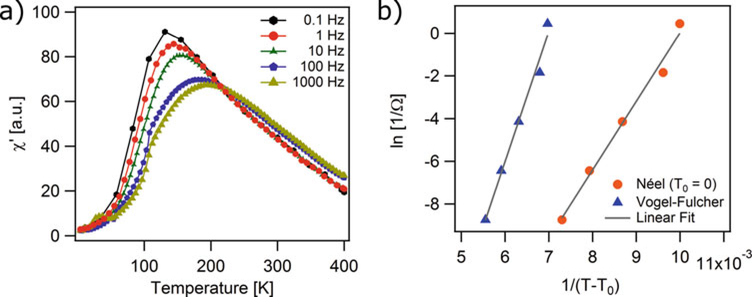
6. The in-phase susceptibility χ′ (T) curves will display a peak at a temperature that decreases as the applied excitation field frequency decreases. It is assumed that at this peak of the χ′ (T) curve the condition Ωτ = 1 applies. To use the Vogel-Fulcher model to interpret the temperature dependence of DMS data [30, 31], plot ln(1/Ω) versus 1/T and compare to the equation

   $$\ln \frac{1}{\mathrm{\Omega }}=\ln {\tau }_0+\left(\frac{K{V}_{\text{m}}}{k_{\text{B}}\left(T-T_0\right)}\right).$$ (10)

   V_m is the magnetic volume. The graph should be linear, with the slope providing an estimate of KV_m and the infinite temperature intercept being a measure of τ₀ (which should be in the range of 10⁻⁹ – 10⁻¹⁴s [32], otherwise indicating significant interactions and casting doubt on the accuracy of the value of K).
7. To account for sample polydispersity, the expression in Eq. (10) is multiplied by the geometric deviation lnσ_g

   $$\ln \frac{1}{\mathrm{\Omega }}=\ln {\tau }_0+\left(\frac{K{V}_{\text{m}}}{k_{\text{B}}\left(T-T_0\right)}\right)\exp \left(\frac{9}{2}\ln {\sigma }_{\text{g}}^2\right)$$ (11)

   In these equations, T₀ can be determined using the methods described in Subheading 3.6, or can be assumed to be T₀ = 0 K in the case of fitting to the Néel model.

8. Figure 5a shows an example of the χ′ (T) curve and Fig. 5b shows the corresponding plot of ln(1/Ω) versus 1/(T − T₀) using the interaction temperature parameter determined with the Vogel-Fulcher model explained in Subheading 3.6 and assuming T₀ = 0 K for the Néel model. The sample was the same sample used in Subheadings 3.5 and 3.6, iron oxide nanoparticles embedded in a PSDVB matrix.

Fig. 5.

(a) In-phase component of the dynamic susceptibility with frequency for iron oxide nanoparticles in a poly(styrene-divinylbenzene) matrix. (b) Inverse applied field frequency as a function of the inverse temperature corresponding to the peak of in-phase component of dynamic susceptibility using the Néel and the Volger-Fuchler model

Table 1 summarizes the values of the anisotropy constant calculated using the temperature-dependent dynamic magnetic susceptibility measurements for magnetic nanoparticles with D_m = 14 nm, lnσ_g = 0.246, and V_m = 1370 nm³, calculated in step 5 of Subheading 3.5 and the value of T₀ = 43.2 K determined from the low field MH measurements described in step 6 of Subheading 3.6. The calculated values are larger than the magnetocrystalline anisotropy constant of bulk magnetite 13.5 kJ/m³ [29], but decrease when the polydispersity of the magnetic diameter and the interaction temperature parameter are included in the analysis.

3.9. Dynamic Magnetic Susceptibility as a Function of Frequency

Dynamic magnetic susceptibility measurements can also be used to determine the mechanism of magnetic relaxation (Néel or Brownian) of a collection of nanoparticles, to estimate the hydrodynamic diameter distribution of particles with predominant Brownian relaxation suspended in a medium of known viscosity, and to determine the viscosity of a liquid with nanoparticles of known hydrodynamic diameter distribution. In these measurements, the dynamic magnetic susceptibility of a sample is measured in a small amplitude oscillating magnetic field at constant temperature and as a function of the frequency of the oscillating magnetic field. Ideally, the amplitude of the oscillating magnetic field remains constant in the whole frequency range of the measurement. However, if the amplitude of the oscillating magnetic field is small enough that the dynamic response is linear with the field amplitude, the measurement can still be completed even if the amplitude of the oscillating field decreases with frequency. Analysis of the frequency dependence of the dynamic magnetic susceptibility can be made for nanoparticles in suspension, for nanoparticles at various temperatures, for nanoparticles suspended in liquids of different viscosities, and for nanoparticles in a solid matrix to obtain information on the mechanism of magnetic relaxation.

1. Suspend the magnetic nanoparticles in a liquid matrix as explained in Subheading 3.3.

2. Set the desired sample temperature (see Note 15).

3. Set the amplitude of the oscillating magnetic field at a value in the range of 2–5 Oe.

4. Measure the dynamic magnetic susceptibility of the sample as a function of decreasing frequency of oscillation (see Note 16 and 17).

5. Use the Debye model to interpret the measurements of DMS as a function of frequency and obtain information of the hydrodynamic diameter of nanoparticles with predominant Brownian relaxation mechanism. According to the model, when an alternating magnetic field of frequency Ω is applied to the sample, the in-phase and out-of-phase components of the dynamic magnetic susceptibility are given by

   $${\chi }^{\prime }={\chi }_{\infty }+\frac{{\chi }_0-{\chi }_{\infty }}{1+{\mathrm{\Omega }}^2{\tau }^2};{\chi }^{\prime \prime }=\frac{\left({\chi }_0-{\chi }_{\infty }\right)\mathrm{\Omega }\tau }{1+{\mathrm{\Omega }}^2{\tau }^2}$$ (12)

   where χ₀ is the low frequency susceptibility, χ_∞is the high frequency susceptibility, and τ is the relaxation time. From Eq. (12), the real component decreases as the frequency increases, whereas the imaginary component has a maximum at Ω_peakτ = 1.
6. To account for polydispersity of nanoparticle hydrodynamic diameters, the susceptibility χ″ in Eq. (12) can be weighed using a lognormal size distribution n_v(D).

   $${\chi }^{\prime }={\int }_{D_{\text{h},0}}^{D_{\text{h},\infty }}{n}_{\text{v}}\left(D_{\text{h}}\right)\times \left[{\chi }_{\infty }+\frac{{\chi }_0-{\chi }_{\infty }}{1+{\mathrm{\Omega }}^2{\tau }^2\left(D_{\text{h}}\right)}\right]\text{d}{D}_{\text{h}}$$ (13)

   $${\chi }^{\prime \prime }={\int }_{D_{\text{h},0}}^{D_{\text{h},\infty }}{n}_{\text{v}}\left(D_{\text{h}}\right)\times \left[\frac{\left({\chi }_0-{\chi }_{\infty }\right)\times \mathrm{\Omega }\tau \left(D_{\text{h}}\right)}{1+{\mathrm{\Omega }}^2{\tau }^2\left(D_{\text{h}}\right)}\right]\text{d}{D}_{\text{h}}$$ (14)

   $$n_{\text{v}}\left(D_{\text{h}}\right)=\frac{1}{\sqrt{2\pi }{D}_{\text{h}}\ln {\sigma }_{\text{g}}}\exp \left(\frac{\ln \left(D_{\text{h}}/D_{\text{hgv}}\right)}{2\left({\ln }^2{\sigma }_{\text{g}}\right)}\right)$$ (15)

   where D_hgv is the volume weighted hydrodynamic diameter, lnσ_g is the geometric deviation, and τ(D_h) is the volume weighted relaxation time corresponding to the volume weighted diameter.
7. Using the relation τ = 1/Ω_peak, obtain the effective relaxation time for a collection of monodisperse nanoparticles. For particles that relax by the Brownian mechanism, τ = τ_B, and the hydrodynamic diameter of the nanoparticles can be calculated using the peak frequency and the relation

   $$D_{\text{h}}=\sqrt{\frac{2k_{\text{B}}T}{\pi \eta {\mathrm{\Omega }}_{\text{peak}}}}$$ (16)

8. Similarly, for nanoparticles with predominant Néel relaxation the peak frequency could in principle be used to determine the magnetic diameter of the nanoparticles or the anisotropy constant. However, in those cases, the peak frequency usually occurs at frequencies that are outside the range of commercially available equipment.

9. To verify if the observed peak corresponds to a Brownian peak, measurements at different temperatures or solvents with different viscosities can be used to observe a shift in the peak frequency due to changes in solvent viscosity, whereas the frequency corresponding to the Néel peak would remain constant [20].

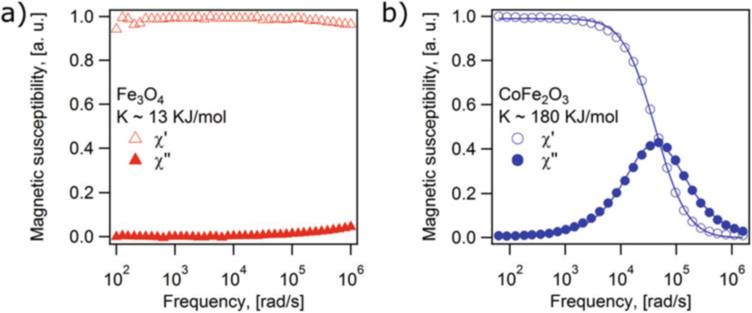
10. Plot the DMS spectra of the magnetic nanoparticle samples. Figure 6 shows examples of DMS spectra for two magnetic nanoparticle samples (cobalt ferrite and iron oxide) in 1-octadecene (η = 0.0412 Pa · s) at 298 K. The difference in the shape of the curves is attributed to the fact that cobalt ferrite nanoparticles possess a much larger anisotropy constant than the iron oxide nanoparticles, and therefore the cobalt ferrite nanoparticles have predominant Brownian relaxation whereas the iron oxide nanoparticles have predominant Néel relaxation. For the iron oxide nanoparticles the peak frequency corresponding to the inverse of the Néel relaxation time would appear at a frequency that is much higher than the maximum frequency that the instrument can apply.

11. Figure 6a corresponds to the DMS spectra of iron oxide nano particles with D_h = 17 nm (lnσ_g = 0.065) and D_m = 14 nm (lnσ_g = 0.246). Assuming the anisotropy constant for the iron oxide nanoparticles corresponds to the bulk value K = 13kJ/mol [33], the Néel relaxation time of the particles is estimated to be τ_N ≈ 9.4 × 10⁻⁸s using Eq. (2), whereas using the hydrodynamic diameter the Brownian relaxation time is estimated to be τ_B ≈ 7.73 × 10⁻⁶s using Eq. (1). Since τ_N ≪ τ_B, the nanoparticles respond primarily through the Néel relaxation mechanism. The corresponding peak frequencies for these two characteristic relaxation times would be 2.6 × 10⁴ rad/s for the Brownian mechanism and 1.7 × 10⁶ rad/s for the Néel relaxation mechanism. The fact that there is no peak at 2.06 × 10⁴ rad/s in Fig. 6a indicates that the Brownian mechanism is not dominant for these nanoparticles. Instead, the Néel relaxation mechanism appears to dominate, but the peak cannot be observed as it is expected to lie over one order of magnitude above the frequency range of the instrument. In fact, it appears that the low-frequency tail of the peak is evident at the highest frequencies in the plot of Fig. 6a, although it is difficult to tell if this is instrument artifact introduced at the extreme frequency range for the instrument.

12. The DMS spectrum of Fig. 6b may be interpreted using similar arguments. In this case the nanoparticles are cobalt ferrite, with a bulk anisotropy constant of K ~ 180 kJ/mol [34]. According to dynamic light scattering measurements of these nanoparticles, the hydrodynamic diameter is D_h = 20 nm (lnσ_g = 0.051). Using Eqs. (1) and (2), the expected Néel relaxation time would be τ_N ≈ 10³⁹s, whereas the expected Brownian relaxation time would be τ_b ≈ 1.26 × 10⁻⁵s. Since τ_b ≪ τ_n, the nanoparticles respond primarily through the Brownian relaxation mechanism. The corresponding peak frequencies are 10⁻⁴⁰rad/s for the Néel mechanism and 7.94 × 10³ rad/s for the Brownian mechanism. The experimental peak frequency Fig. 6b is Ω_peak = 4.78 × 10⁴ rad/s (7.61 × 10³ Hz). The close agreement between the experimental and Brownian peak frequencies indicates that this sample responds predominantly through Brownian relaxation.

Fig. 6.

DMS spectra for liquid samples of (a) iron oxide and (b) cobalt ferrite nanoparticles in 1-octadecene at 298 K