Figure 1.

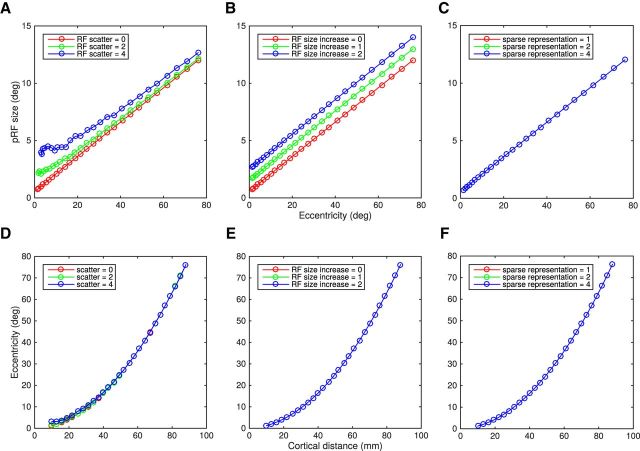
Effect of different types of neuronal disturbances in pRF and CMF estimation from simulation. pRFs were built and sampled regularly across a cortical surface. Position, shape, and size parameters of area V1 were taken from Harvey and Dumoulin (2011). The pRF is estimated from the total neuronal population within a voxel. Hence the properties of all the individual neurons influence the estimated pRF. Simulations were one-dimensional only. Each neuron was described as one point within the cortex represented by a line, the coordinates set between 0 (center of the fovea) and 100 mm. The relationship between CMF and eccentricity was calculated according to Equation 2 (Harvey and Dumoulin, 2011): CMF (mm/deg) = $\frac{1}{cx+d}$, with c = 0.04 mm⁻¹ and d = 0.07°/mm based on that study. The position of the neuron's receptive field (RFmm) were computed from the integral of 1/CMF: RFmm = $\frac{c}{2}$ · mm² + d · mm, where mm is the linear distance in millimeters from the center of the fovea. The size of the neuron's receptive field (RFsize) was calculated according to Equation 1: Rfsize(°) = a. RFmm + b, with a = 0.15°/° and b = 0.48°, based on that study (Harvey and Dumoulin, 2011). A–C, Top row shows pRF size versus eccentricity. D–F, Bottom shows the CMF, cortical distance versus eccentricity. Left column (A, D) shows the effect of different position scatters of the individual neurons (no scatter in red, 2° in green, and 4° in blue). Increasing RF scatter leads to an increase of pRF size (Zuiderbaan et al., 2012) while CMF is hardly affected. Interestingly, the pRF intercept follows the RF scatter closely. B, E, Middle column, Effect of increasing the individual RF sizes (original size in red, +2° in green, and +4° in blue). An increase of RF size provokes an increase of the pRF sizes across all eccentricities but CMF is not affected. C, F, Right column, Effect of reducing the number of neurons within a voxel by sparsely sampling the RFs (fewer RFs contributing to the signal). A sparse representation of 1 means that all RFs were sampled, a sparse representation of 2 corresponds to sample every other RFs, a sparse representation of four corresponds to sample every four RFs. Decreasing the sampling does not lead to any change either in pRF size or in CMF. In all cases, red lines show the same original scenario.