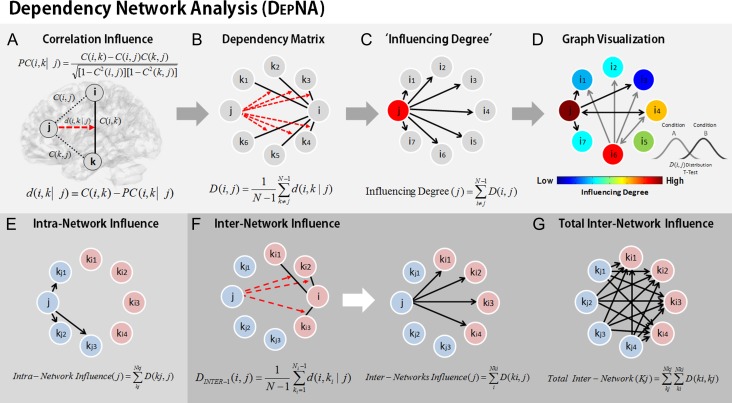
Figure 2.
Dependency network analysis (DEPNA). (A) The correlation influence of node j on the pair of nodes i and k is defined as the difference between their correlation C(i,k) and their partial correlation with respect to the node j − PC(i,k|j). The partial correlation coefficient is a statistical measure indicating how a third variable affects the correlation between 2 other variables. Thus, the correlation influence measure d is large only when a significant fraction of the correlation between nodes i and k can be explained by the influence of node j. (B) Dependency matrix—next, we calculate the partial correlation effect for each ROI on all other pairwise correlations in the network. We define the total influence of node j on node i, D(i,j) as the average influence of node j on the correlations C(i,k), over all nodes k. The node dependencies define a dependency matrix D, whose (i,j) element is the influence of node j on node i. (C) “Influencing Degree”—we then define the influences of node j as the sum of the influence D(i,j) of j on all other nodes i. The higher this measure the more this node influenced all other connections in the network. (D) Graph Visualization—each ROI is color-coded according to its influencing or influenced degrees. All pairwise ROIs with dependency elements D that are significantly different between 2 conditions (or groups) at the P < 0.001 level are plotted as edges. Each edge is color-coded according to the t-test sign as light or dark gray. The arrows represent the direction of influence. (E) The intranetwork influence was computed for each node as the sum of its influences on the nodes within its network. (F) The internetwork influence was calculated as the sum of the influences D(ki,j) of a node j from one network only on the nodes ki in the second network. Each region gets a measure of its influence on the connections of the second network. (G) The total internetwork influence was computed as the sum of all internetwork influences from one network on the nodes within the second network.