Fig. 1. Two-step inverse design process.
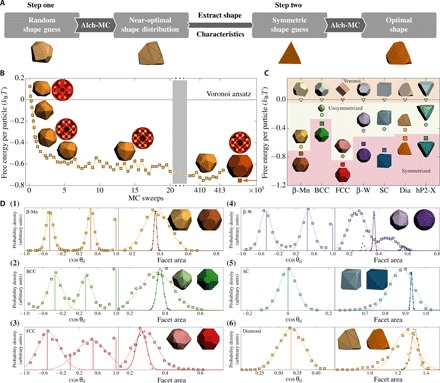
(A) Schematic diagram illustrating the process. In step one, Alch-MC starts from a random convex shape and then finds an unsymmetrized optimal shape for the target structure (here, diamond). Cosine of dihedral angle distribution and PMFT isosurface of the unsymmetrized optimal shape reveals that it has tetrahedral characteristics. In the second step, fluctuating particle shape Alch-MC simulation starts from a tetrahedron and finds an optimal symmetrized shape for the diamond structure. (B) Alch-MC for the inverse design of an unsymmetrized thermodynamically optimal hard particle shape to form a target structure (here, β-Mn). The structure is imposed by an auxiliary design criterion, and detailed balance drives particles to take on shapes (selected shapes are displayed in light yellow) that are favorable for the target structure (indicated by selected bond order diagrams). Directly computed free energy confirms that Alch-MC simulation over ≳105 distinct shapes converges to shapes that have lower free energy (by ≈0.7 kBT per particle; numerical errors are smaller than markers) than shapes chosen by Voronoi construction. Desired shape features can be inferred from the equilibrium particle shape distribution and used to create a symmetry-restricted ansatz, which yields a thermodynamically optimal synthesizable shape (shown in dark yellow). (C) Direct free energy comparison of our entropic engineering strategy for seven target structures: β-Mn, BCC, FCC, β-W, SC, diamond, and hP2-X. For each structure, we calculated the free energy of the target crystal for a shape formed from a geometric ansatz based on the Voronoi decomposition of the structure (triangles). Compared with the Voronoi ansatz, we find that Alch-MC simulation over arbitrary convex polyhedra in step one produces shapes (circles) that spontaneously self-assemble the target structures with higher entropy. Symmetry-restricted polyhedra (squares) (truncated polyhedra for β-Mn, BCC, and FCC; truncated and vertex-augmented polyhedra for β-W, SC, diamond, and hP2-X) inferred from shapes in step one produce putatively thermodynamically optimal particle shapes by maximizing entropy. (D) Two-step shape Alch-MC entropic particle shape optimization for six target structures: β-Mn, BCC, FCC, β-W, SC, and diamond. For each target structure, an initial Alch-MC simulation over 92- or 188-dimensional spaces of convex polyhedra in step one converged to highly faceted modifications of identifiable Platonic, Archimedean, or Catalan solids, obtained by calculation of the equilibrium distribution of the cosine of dihedral angles cosθd (left, light color, squares) and facet areas (right, light color, squares) (Gaussian distributions are plotted with solid lines for comparison). We show the mean of the cosine of dihedral angle distributions in table S1. In step two, Alch-MC simulation over symmetry-restricted families of shapes determined a thermodynamically optimal and synthesizable shape (shown in dark color). For each target structure, we calculate the equilibrium distribution of the cosine of dihedral angles cosθd (left, dark color, vertical line) and facet areas for symmetrized optimal shapes (right, dark color points, with Gaussian distribution fitting). The distributions are in arbitrary units. In all cases, representative shapes spontaneously self-assembled target structures in NVT simulations, with periodic boundary condition satisfied.
