Efficient merging of genome profile alignments

Abstract

Motivation

Whole-genome alignment (WGA) methods show insufficient scalability toward the generation of large-scale WGAs. Profile alignment-based approaches revolutionized the fields of multiple sequence alignment construction methods by significantly reducing computational complexity and runtime. However, WGAs need to consider genomic rearrangements between genomes, which make the profile-based extension of several whole-genomes challenging. Currently, none of the available methods offer the possibility to align or extend WGA profiles.

Results

Here, we present genome profile alignment, an approach that aligns the profiles of WGAs and that is capable of producing large-scale WGAs many times faster than conventional methods. Our concept relies on already available whole-genome aligners, which are used to compute several smaller sets of aligned genomes that are combined to a full WGA with a divide and conquer approach. To align or extend WGA profiles, we make use of the SuperGenome data structure, which features a bidirectional mapping between individual sequence and alignment coordinates. This data structure is used to efficiently transfer different coordinate systems into a common one based on the principles of profiles alignments. The approach allows the computation of a WGA where alignments are subsequently merged along a guide tree. The current implementation uses progressiveMauve and offers the possibility for parallel computation of independent genome alignments. Our results based on various bacterial datasets up to several hundred genomes show that we can reduce the runtime from months to hours with a quality that is negligibly worse than the WGA computed with the conventional progressiveMauve tool.

Availability and implementation

GPA is freely available at https://lambda.informatik.uni-tuebingen.de/gitlab/ahennig/GPA. GPA is implemented in Java, uses progressiveMauve and offers a parallel computation of WGAs.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Whole-genome sequencing (WGS) has become increasingly affordable due to the continuous developments of next-generation sequencing technologies. WGS for example is now routinely conducted in a clinical context to monitor pandemic bacterial outbreaks based on the sequencing of different isolates. Single nucleotide polymorphisms (SNPs) between isolates and a reference genome can help to understand and reconstruct transmission chains (Bryant et al., 2013; Sabat et al., 2013). The disadvantage using a single reference to compare different individuals is that features missing from the reference cannot be detected. Especially in the absence of a closely related reference genome, such an approach is not appropriate (Abdelbary et al., 2018). To overcome this problem, an increasing number of studies incorporate the pan-genome of the species into the analysis of different isolates. Here, gene content and genomic rearrangements such as insertions, deletions, translocations and inversions are used to explain the manifestation of phenotypic traits like antibiotic resistance (Medini et al., 2005). One approach to compute a pan-genome is based on whole-genome alignments (WGAs) [see for example Angiuoli et al. (2011); Hennig et al. (2015); Schatz et al. (2014)]. In comparison to a BLAST-based approach or variants of it which are employed to compute orthologous gene groups, the WGA-based approach has the advantage that for the identification of orthologous genes gene neighborhood is taken into account. In addition, the pan-genome based on a WGA can be generalized to consider also nongenic features. Further applications of WGAs encompass the identification of pathogenic genomic islands or reconstruction of phylogenomic trees (Chan and Ragan, 2013).

Runtimes of current state-of-the-art aligners that are capable of modeling genomic rearrangements, such as progressiveMauve (Darling et al., 2010), are at least quadratic in the number of genomes. Thus, computation of WGAs of hundreds or thousands of even closely related bacterial genomes with state-of-the-art tools are prohibitive. Currently only Parsnp (Treangen et al., 2014) is able to compute large-scale alignments with hundreds or even thousands of genomes within hours. However, it computes only a core-genome alignment. While Parsnp is a highly valuable tool for the identification of SNPs from the core pan-genome, it does not allow for the detection of genomic rearrangements and pathogenic islands for example. Recent advances in the field of WGA methods were made with the introduction of seq-seq-pan (Jandrasits et al., 2018), which offers the efficient extension of existing WGA by new genomes. Through a pairwise iterative alignment process, new genomic sequences are aligned against the consensus sequence of the alignment, which shows a substantial runtime decrease while achieving comparably high-quality alignments.

seq-seq-pan makes use of the profile of a pairwise alignment (and deduces a consensus sequence) for extension by new sequences. Using a profile as a representation for an alignment is a popular concept for calculating multiple sequence alignments (MSA) and was first introduced by Hogeweg and Hesper (1984) in their progressive alignment heuristic. The idea to progressively compute MSAs along a guide tree, where at each node either a pairwise alignment between sequences, a sequence and a profile or two profiles are conducted, reduces the runtime significantly in contrast to the construction of an optimal alignment that maximizes the sum of pairs score for example. Especially the profile–profile alignment offers a fast and efficient way to combine two separate alignments. Recent advances in this field have been made by Liu and Warnow (2014) with the idea of a divide and conquer approach to compute smaller subsets of alignments which are merged through a profile–profile alignment. The parallel computation of the subset alignments further reduces the computational runtime, while still achieving highly accurate results.However, currently such a profile alignment-based approach is missing in state-of-the-art alignment tools such as progressiveMauve. Since WGAs need to consider genomic rearrangements, such as translocations and inversions, between the individual genomes, a profile alignment of two or more WGAs is more difficult than a profile alignment of MSAs. Here, we introduce our concept for the first profile–profile alignment of WGAs. The profile-based merging of WGAs is conducted with the help of our SuperGenome data structure (Herbig et al., 2012), which can be used to transfer different WGA-coordinate systems into a common one.

Based on this profile-based alignment approach, we implemented GPA (genome profile alignment), a software that can align hundreds to thousands of genomes in a fast and efficient manner. The goals of our WGA construction strategy were to adopt the advances from the field of profile-based MSA tools, and therefore significantly reduce computational time and still achieving highly accurate WGAs. Our intention was not to develop a new genome alignment algorithm. Therefore, GPA relies on other whole-genome aligners but using a divide and conquer strategy to merge subsets of alignments along a guide tree. In our current release, we have combined progressiveMauve with our profile-based approach.

The article is organized as follows: In Section 2, we first present the SuperGenome data structure and the algorithmic principles that allow an efficient merging of several alignments. The critical aspect is the transfer of different coordinate systems into a common one, which is supported by the SuperGenome. We explain in detail the extension of a given WGA by other genomes or other WGAs. Based on this, we then explain how to compute large-scale WGAs from scratch in a fast and parallelized manner. The section concludes with a description of statistics that we used to compare and evaluate our approach with the original progressiveMauve. The Section 3 presents the evaluation of the WGAs computed for different simulated as well as real biological datasets by progressiveMauve and GPA. The evaluation is focused on the runtime needed and the achieved quality of the WGA by both approaches. Finally, we conclude this article with a critical discussion of our results and propose future extensions of our approach.

2 Materials and methods

2.1 SuperGenome data structure and construction

In comparison to MSA, where the order of nucleotides within each sequence is assumed to be preserved, aligning whole-genomes has to consider the occurrence of rearrangements, such as translocations as well as inversions. Regions shared by two or more genomes that do not contain any rearrangements of homologous sequences are called locally collinear blocks (LCBs), and a WGA is typically then represented by a set of such LCBs. Programs computing WGAs of this form are for example Mauve (Darling et al., 2004), progressiveMauve (Darling et al., 2010), Mugsy (Angiuoli and Salzberg, 2011) and TBA (Blanchette et al., 2004). The SuperGenome is a data structure, which makes use of a WGA and features a bidirectional mapping between the alignment coordinates and the original coordinates of each individual genome in the WGA (Herbig et al., 2012). The main advantage of the SuperGenome data structure is that it provides an unambiguous coordinate system and is independent of any prechosen reference genome.

We will first introduce some formal terminology before we then describe the algorithm to compute large-scale WGAs to decrease computational runtime using a profile-based approach together with the SuperGenome data structures derived from the profiles.

Given are n genomes $g_i,i=1,\dots ,n$ and a WGA $\mathbf{A}$ on these n genomes. For every genome, we define a pair of integer arrays G_i and SG_i, which provides the bidirectional mapping between the genomic positions of g_i and alignment positions of $\mathbf{A}$. Let us assume that the j-th base of g_i is aligned at the k-th position in $\mathbf{A}$. Thus, G_i, representing the mapping of g_i to $\mathbf{A}$, contains the value k at entry j. In the case that the base was aligned as its reverse complement (i.e., representing an inversion), the value of k is negative:

$$G_i[j]=\{\begin{array}{c} k,\hspace{0.17em} \text{if}\hspace{0.17em}\text{base}\hspace{0.17em}j\hspace{0.17em}\text{is}\hspace{0.17em}\text{aligned}\hspace{0.17em}\text{in}\hspace{0.17em}\text{forward}\hspace{0.17em}\text{orientation}\hspace{0.17em}\hfill \\ -k,\hspace{0.17em} \text{if}\hspace{0.17em}\text{base}\hspace{0.17em}j\hspace{0.17em}\hspace{0.17em}\text{is}\hspace{0.17em}\text{aligned}\hspace{0.17em}\text{as}\hspace{0.17em}\text{reverse}\hspace{0.17em}\text{complement}\hspace{0.17em}\hfill \end{array}$$ (1)

The respective SuperGenome array SG_i represents the mapping of the aligned sequence of genome g_i in $\mathbf{A}$ and is analogous to G_i. In addition, it also accounts for gaps. In case at position k in $\mathbf{A}$ no base of g_i was aligned the entry is set to zero:

$$S{G}_i[k]=\{\begin{array}{c} j,\hspace{0.17em} \text{if}\hspace{0.17em}\text{base}\hspace{0.17em}j\hspace{0.17em}\text{is}\hspace{0.17em}\text{aligned}\hspace{0.17em}\text{in}\hspace{0.17em}\text{forward}\hspace{0.17em}\text{orientation}\hspace{0.17em}\hfill \\ -j,\hspace{0.17em} \text{if}\hspace{0.17em}\text{base}\hspace{0.17em}j\hspace{0.17em}\text{is}\hspace{0.17em}\text{aligned}\hspace{0.17em}\text{as}\hspace{0.17em}\text{reverse}\hspace{0.17em}\text{complement}\hspace{0.17em}\hfill \\ 0, \hspace{0.17em}\text{if}\hspace{0.17em}\text{no}\hspace{0.17em}\text{base}\hspace{0.17em}\text{of}\hspace{0.17em}{g}_{\mathrm{i}}\hspace{0.17em}\text{aligns}\hspace{0.17em}\text{at}\hspace{0.17em}\text{that}\hspace{0.17em}\text{position}\hspace{0.17em}\hfill \end{array}$$ (2)

An example illustrating the concept of the two arrays is shown in Figure 1A.

Fig. 1.

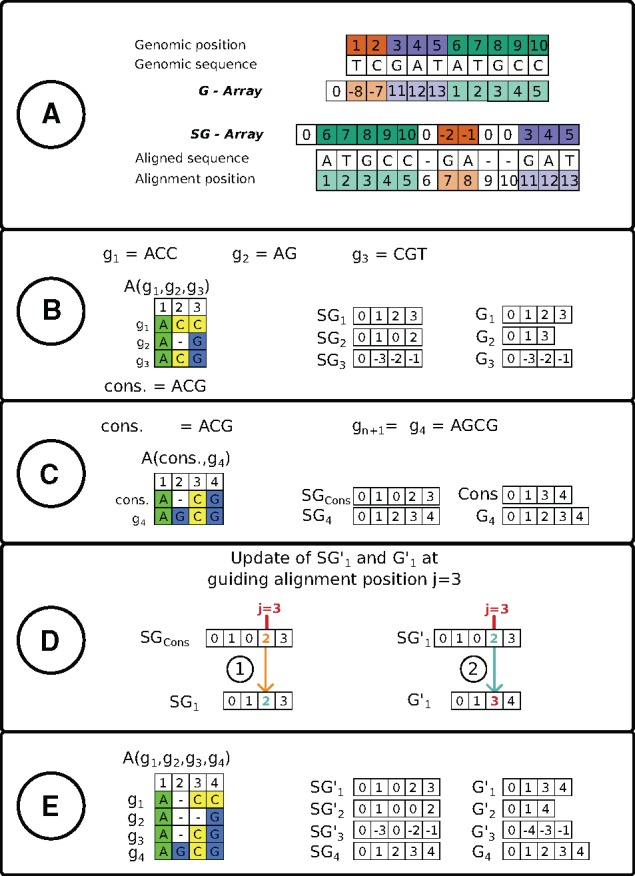
(A) Example of the SuperGenome data structure with its arrays G and SG for a genome with its aligned genomic sequence. As visually encoded, the array G resembles the alignment position for each base, while SG stores the genomic positions of the aligned bases. Negative values in G and SG indicate the alignment of the reversed complement of the base. (B) Based on the three genomic sequences g₁, g₂ and g₃ and their alignment $\mathbf{A}(g_1,g_2,g_3)$, a SuperGenome data structure (union of the SG and G arrays) is computed. In addition, a consensus sequence from the alignment is deduced. (C) A new genomic sequence g₄ is combined with $\mathbf{A}(g_1,g_2,g_3)$. For this a pairwise alignment $\mathbf{A}(\mathit{cons},g_4)$ is computed and again a SuperGenome data structure is deduced. (D) Update of $\mathbf{A}$ by g₄: for every position j in $\mathbf{A}(\mathit{cons},g_4)$, (1) array $S{G}_{\mathit{cons}}[j]$ (orange) contains the index of the aligned consensus sequence positions, which is used to determine the original genomic positions $S{G}_1[S{G}_{\mathit{cons}}[j]]$ (example shown in blue). (2) This allows a coordinate transfer $\mathit{SG}{\prime }_1[j]=S{G}_1[S{G}_{\mathit{cons}}[j]]$ and $G{\prime }_1[\mathit{SG}{\prime }_1[j]]=j$ (red) into a common coordinate system of $\mathbf{A}(\mathit{cons},g_4)$. (E) From the updated SuperGenome data structure the new alignment $\mathbf{A}(g_1,g_2,g_3,g_4)$ is easily deduced

These two arrays enable a simple way to deduce information from the WGA. For alignment position k it is easy to determine which individual genomic positions are aligned with each other by accessing $S{G}_i[k]$ for each genome g_i. Vice versa, to determine which bases are aligned to a specific base j from g_i, the image of $G_i[j]$ is computed and the respective entry in the SG arrays is then used as above.

For a given WGA of n genomes, the generation of the data structure is straightforward. For each genome, the pair of arrays G_i and SG_i is first initialized with the corresponding lengths of g_i and $\mathbf{A}$, respectively, containing only zeros for each entry. To simplify the handling of the 0-based array structure of Java, the arrays have a leading entry (set to zero), resulting such that the j-th entry of the array represents the j-th position in the genome or the alignment. Through an iteration over every alignment position, the arrays are filled, resulting in a total of $2\times n$ arrays with a space requirement of $n\times$ length of the alignment and the sum of all genome lengths.

In addition to the coordinate mapping, the SuperGenome takes the LCB structure into account, as for example, computed by progressiveMauve and stored in XMFA-format. The coordinate system of the alignment and its mapping to the genomic position, thus the SG arrays, is based on the concatenation of the individual LCBs contained in the XMFA-file. For the construction of the data structure the ordering of the LCB does not matter, however for consistency we simply using the predefined ordering of the input file. Furthermore, this ordering and the lengths of the LCBs are stored to allow the inference of the LCBs from the SG arrays. For example, for two LCBs of length n and m, respectively, the array positions $\mathit{SG}[1,\dots ,n]$ and $\mathit{SG}[n+1,\dots ,n+m]$ represent these two LCBs.

From the SuperGenome data structure, the WGA can be derived from the arrays SG_i, where each aligned sequence of g_i can be reconstructed iteratively back from the genomic positions of the entries. Here, inversions (negative values) and gaps (zeroes) have to be taken into account.

2.2 Extending an existing WGA

We now first describe how a new genome is added to an existing WGA on n genomes using the SuperGenome approach. Then we show how to extend this principle to merging two WGAs on n and m genomes, respectively, into a WGA on n + m genomes. The general idea is that for the extension step only a pairwise alignment is computed. This concept can then be generalized to several alignments and genomes that are combined into a WGA of all involved genomes.

A common approach to make use of an existing alignment $\mathbf{A}$ is a profile alignment, which preserves all prior aligned positions. The profile of $\mathbf{A}$ is represented by a consensus sequence, which is derived from the SuperGenome data structure through a majority call on all alignment positions of $\mathbf{A}$ (see Fig. 1B for an example). For the integration of a new genome $g_{n+1}$ into $\mathbf{A}$, unique regions of $g_{n+1}$ and homologous regions of $g_{n+1}$ and the profile have to be computed in order to extend $\mathbf{A}$ by $g_{n+1}$. This is achieved by computing a pairwise alignment of the profile consensus sequence and the genomic sequence $g_{n+1}$. This pairwise alignment serves as a guiding alignment to extend the given alignment $\mathbf{A}$ by the new genome $g_{n+1}$. Again we use the SuperGenome data structure for this step (see Fig. 1C–E for an illustration of this procedure). For this, the SuperGenome data structure of the pairwise alignment is computed, which includes the array SG_cons with all positions of the profile consensus sequence and $S{G}_{n+1}$, the SG array of genome $g_{n+1}$. The extension of A comprises the transfer of the coordinates of SG_i and G_i for the n genomes into the common coordinate system of $S{G}_{\text{cons}}$ and $S{G}_{n+1}$. The new bidirectional coordinate mappings $\mathit{SG}{\prime }_i$ and $G{\prime }_i$ for genome g_i are derived by

$$\mathit{SG}{\prime }_i[j]=S{G}_i[S{G}_{\mathit{cons}}[j]] \text{and} \mathrm{G}{\prime }_{\mathrm{i}}[\text{SG}{\prime }_{\mathrm{i}}[\mathrm{j}]]=\mathrm{j}$$ (3)

where $S{G}_{\mathit{cons}}[j]$ is the index of the consensus sequence, which is aligned at position j in the pairwise alignment, and $S{G}_i[S{G}_{\mathit{cons}}[j]]$ the index of the base of g_i that was aligned in $\mathbf{A}$.This coordinate transfer restores all columns of alignment $\mathbf{A}$. The arrays $S{G}_{n+1}$ and $G_{n+1}$ do not have to be updated, since they are already consistent with the coordinate system of the guiding alignment. Based on the updated SuperGenome data structure on n + 1 genomes, the new alignment can now be easily derived and written into the alignment format as described above.

The procedure for adding one genome to a WGA is easily extended to merging the profiles of two WGAs on n > 1 and m > 1 genomes, respectively. Again, we compute a pairwise alignment, now on the two respective consensus sequences, derive the respective SuperGenome, which together with the SuperGenome of the input WGAs is used to update the bidirectional mappings [see Equation (3)] of the two WGAs. A consequence of this merging procedure is that prior aligned bases remain aligned in the merged WGA.

Finally, it is straightforward to generalize the pairwise approach to combining more than two WGAs or WGAs with individual genome sequences. Rather than aligning only two sequences, we compute the multiple genome alignment of all consensus sequences derived from the k > 2 individual WGAs as well as possible single genome sequences. The generalized workflow of merging several WGAs into a common WGA can be summarized in the following six steps (see also Fig. 2):

Fig. 2.

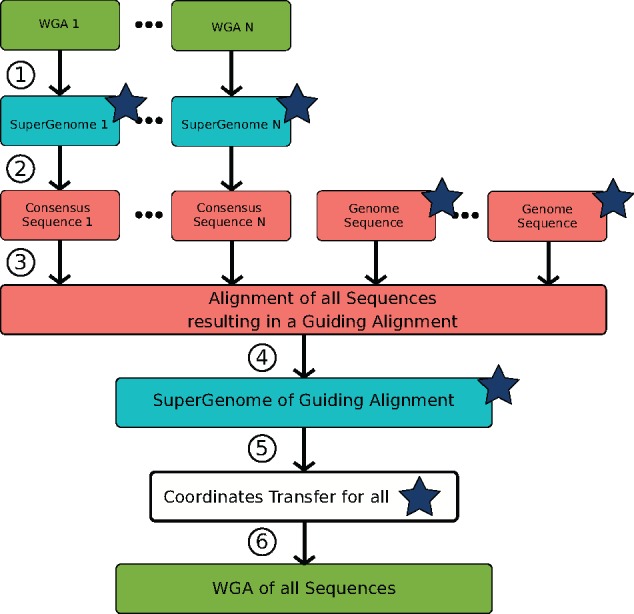
Workflow of merging several alignment and genomes using the SuperGenome data structure into a large WGA. The workflow consists of six steps: (1) Build SuperGenome for every alignment, (2) compute consensus sequence from input alignments, (3) align all consensus and genome sequences, (4) build SuperGenome of guiding alignment, (5) merge all alignments and genomes (marked with a star) via coordinates transfer and (6) output alignment of all sequences in XMFA-format derived from updated SuperGenome data structure

1. Construct SuperGenome data structure for every input alignment.

2. For every SuperGenome compute a consensus sequence (output in FASTA format).

3. Align consensus sequences as well as possible individual genome sequences with whole-genome aligner (e.g., using progressiveMauve) to generate the guiding alignment.

4. Construct SuperGenome data structure for the guiding alignment.

5. For every genome i, update SG_i and G_i according to Equation (3).

6. Output new alignment derived from updated $\mathit{SG}\prime$ and $G\prime$ (output in XMFA-format).

The merged WGA also accounts for LCB structures from the input alignments. Previous start and stop positions in SG, which determine the borders of a LCB, are transferred and added to the ones introduced by the guiding alignment. The resulting LCBs of the merged WGA are defined between every consecutive pair of LCB border positions in SG originating from the different WGAs that are merged to secure the LCB property that no rearrangements within a block occur.

2.3 Genome profile alignment

We have implemented the described approach how to efficiently merge several WGAs or to extend a given WGA by new genomes using our SuperGenome data structure in the tool which we call GPA. Our tool is written in Java and can be run on any machine with a Java VM installed. For the computation of the WGAs, we currently make use of progressiveMauve, which needs to be installed independently.

GPA can be applied in two ways: it can align genome sequences from scratch, or it can be used to extend an existing WGA by new genomes. In the first case, the input data are the genome sequences that need to be provided in FASTA format. Since the general idea of our approach is to combine smaller sets of aligned genomes to a full WGA, these smaller sets first have to be defined. For this, we either make use of a guide tree, which determines the individual merging steps, or all genome sequences are randomly distributed into subsets, where the size of the subsets has to be predefined by the user. The guide tree needs to be provided by the user in Newick tree format and can, for example, be the one as computed by progressiveMauve. As most guide trees are binary and only two sequences are aligned at each node, the provided input tree is further modified, to control the number of sequences/WGAs that are aligned in each step. With a user-defined maximum number of sequences aligned in each step, the nodes of the guide tree (representing the set of sequences which will be aligned) are propagated from the leaves (representing the genomes) toward the root (representing the final WGA) until another propagation to the next node of the tree would exceed the maximum. This modified guide tree is used to compute an internal guide tree structure. In the next step, after the internal guide tree structure has been built, GPA automatically creates a folder structure, which serves to save the WGAs from the intermediate steps in XMFA-format. The computation of the WGAs follows the typical process of progressive alignments, starting at the leaves of the guide tree and the root represents the full WGA. If no guide tree has been provided, GPA merges all WGAs of the individual subsets into a common WGA in one step. To further decrease the runtime, GPA provides the possibility to compute the independent subalignments in parallel.

The second application case is to extend an existing WGA. For this, GPA can be provided with an arbitrary number of WGAs and single genomes. Here, the respective profiles or genomic sequences are aligned in one step. The final WGA then contains all new genomes as well as those which were contained in the input WGAs. Note that in fact the second case is used throughout the computation of a WGA from scratch when using our approach in GPA.

2.4 Experimental setup

2.4.1 Evaluation criteria

Besides runtime assessment, we used three different statistics to compare the WGA computed using our guide tree-based SuperGenome approach with the WGA computed by applying progressiveMauve to all genomes at once: pairwise consistency score, total column score and F-score.

The pairwise consistency (PC) score reflects how much the WGA agrees with all possible pairwise alignments, a concept which was first described by Gotoh (1990) and adapted in T-COFFEE (Notredame et al., 2000). For this, for each pair of genomes in the WGA, we compute the percentage of bases that are consistently aligned in the WGA and in the respective pairwise genome alignment. For a given WGA of n genomes, we then report the average PC score from all $\left(\begin{array}{c}n\\ 2\end{array}\right)$ scores.

The total column (TC) score, first introduced in BaliBase (Thompson et al., 2005), equals the percentage of identically aligned columns in a given alignment when compared with a given reference alignment.

The third statistic, the F-score, is the harmonic mean of precision and recall for identical pairwise aligned bases. The F-score was used in the Alignathon competition (https://compbio.soe.ucsc.edu/alignathon/) for the comparison of two WGAs (Earl et al., 2014), where one of the two WGAs serves as a reference.

All three statistics have been widely used to evaluate MSA methods. The TC score is very conservative and prone to small changes in the alignment, since one misaligned sequence can drastically decrease the score. Therefore, comparing the best MSA methods may only result in low TC scores. On the other hand, only slight differences in the PC score between two alignments, as well as a high TC and F-score, are reliable indicators for the similarity of the two. For the calculation of all scores when comparing two WGAs, one needs to take care of possible inversions and translocations. Again, the SuperGenome data structure serves extremely useful for this, and therefore we also used it for the calculation of these scores.

2.4.2 Simulated datasets

To evaluate the performance of GPA in the context of a ‘ground truth’, where the optimal WGA is known, we used the same genome simulation approach as the Alignathon. The simulated genomes were generated with the software EVOLVER (Edgar et al., 2009) together with the evolverSimControl suite (Edgar et al., 2012), that is able to evolve genomes based on a given phylogenetic tree and report the respective WGA. The simulation parameters required for the evolverSimControl suite were used from the EVOLVER example and adapted to prohibit duplication events, since Mauve cannot address duplication events. The F-scores between the simulated and GPA generated WGAs were calculated with mafTools (Earl et al., 2014) (https://github.com/dentearl/mafTools/).

2.4.3 Biological datasets

To explore the performance of GPA, we applied our approach to a large number of complete single chromosome bacterial genomes from the same species which we derived from NCBI (ftp://ftp.ncbi.nlm.nih.gov/genomes). The various datasets reflect different genome lengths and sizes as well as diversities of genomes within a species to explore the performance of GPA. Currently, GPA can only handle single sequences per genome. However, it is possible to concatenate the different chromosomes (or plasmids) of one genome to overcome this limitation. Still, we decided to remove all possible plasmids prior to the WGA computation and only computed single chromosome alignments. All datasets used in this work are listed in Table 1 together with the total number of genomes as well as the average genome length and average GC content (source https://www.ncbi.nlm.nih.gov/).

Table 1.

The datasets, which were used for the WGA computations as obtained from the NCBI FTP server

Organism	No. of Strains	Median genome length (Mb)	GC content (%)
B.cereus	13	5.760	35.1
L. monocytogenes	30	2.975	37.9
C.trachomatis	72	1.046	41.3
M.tuberculosis	128	4.385	65.6
K.pneumoniae	166	5.590	57.2
S.aureus	176	2.847	32.8
B.pertussis	326	4.100	67.7

Note: All statistics including the median genome length and median GC content have been derived from NCBI.

2.4.4 Computational platform

We ran all WGA computations on a Linux server with four Intel(R) 197 Xeon(R) CPU E5-4610 v2 @ 2.30GHz and 500 GB of memory. We measured the runtime with the GNU time command. During all WGA computations, GPA used the maximal number of threads needed to ensure that all independent subset alignments could be computed in parallel.

3 Results

With GPA, we have extended progressiveMauve by the possibility to provide an existing sequence alignment in XMFA-format and align it to other sequences or alignments. Traditionally, profile alignment is conducted on a pairwise level, however, with GPA a multiple profile alignment can be computed in one step. With this feature, a progressive alignment strategy that is typically performed along a binary guide tree can now be generalized to nonbinary trees with fewer internal nodes. GPA provides a parameter k, that controls the maximal degree of multifurcation of every internal node and therefore how many genomes and/or profiles are merged at each step. Our overall intention for this strategy was to multiply align up to hundreds or more bacterial genomes with a significantly reduced runtime and at the same time achieve highly qualitative WGAs. We first evaluated the WGAs computed by GPA based on simulations, followed by comparison of the WGAs computed for real biological datasets.

3.1 Evaluation based on simulated data

We simulated five different WGAs of different sizes, where we used the genome of Bordetella pertussis (RefSeq ID: NC_002929.2) as the start of the simulation as well as the guide trees computed from real biological genomes (see below) using progressiveMauve. The simulations were all independent of each other. Therefore a comparison of the PC, TC and F-scores across the WGAs of different size is misleading because only the phylogenetic origin of the simulated dataset is same. Here, the focus is set on comparing the performance of the iterative profile alignment approach of GPA with progressiveMauve. For GPA, WGAs with different merge sizes k were computed, the one with the highest F-score is reported. For the evaluations based on the TC scores we either use the simulated alignment (as computed by EVOLVER) or the alignment computed by progressiveMauve at once as a reference.

As can be seen from the results (see Table 2) the computation of the WGA by GPA is not only significantly faster than computation by progressiveMauve, but also the runtime difference increases drastically with increasing number of genomes. At the same time, the WGA computed by GPA is highly comparable to the one computed by progressiveMauve. Both WGA computation approaches yield highly similar PC and TC scores (with the simulated alignment as the reference), which differ in less than 2%. Also, the combination of high TC (>60%) and F-scores (>0.98) between the respective WGAs of both tools shows their high conformity. In addition, the F-scores, derived from the comparison of the WGA as computed by progressiveMauve and GPA, respectively, with the simulated, ‘ground truth’ WGA are almost identical. The largest difference between both approaches besides runtime is the memory needed to construct the alignment. Here, GPA needs around three to five times more memory than progressiveMauve to compute the WGAs. An exception for this is WGA computation of 80 simulated strains, where the increase of memory consumption as well as runtime of progressiveMauve is extraordinary. The simulation was repeated several times, and the large runtime and memory consumption was confirmed for each run.

Table 2.

Evaluation of WGAs generated by progressiveMauve (PM) and GPA based on simulated WGAs by EVOLVER (EVO)

	Runtime [min]		PC score		F-score	F-score	F-score	TC score	TC score	TC score	Memory usage [GB]
No. of Strains	PM	GPA	PM	GPA	PM with EVO	GPA with EVO	PM with GPA	GPA in PM	PM in EVO	GPA in EVO	PM	GPA
10	26	8	97.27%	97.12%	0.985	0.985	0.992	92.54%	92.26%	90.39%	0.72	2.50
20	125	39	98.28%	98.24%	0.997	0.996	0.996	93.94%	96.40%	95.36%	1.34	4.59
40	678	121	94.78%	93.86%	0.976	0.971	0.990	62.84%	60.18%	58.74%	2.33	10.14
80	14541	163	94.49%	95.02%	0.976	0.977	0.984	63.67%	68.03%	70.68%	23.11	16.83
326	—	653	—	88.14%	—	0.948	—	—	—	14.13%	—	47.21

Note: All WGAs were evaluated with respect to their runtime (wall-clock time), average PC, F-scores achieved against EVO and maximal amount of RAM used in the process of WGA computation. In addition the TC score and F-score between PM and GPA is reported. Again, for the calculation of the TC and F-score, PM is used as the reference. GPA was run with several different parameters k for the merge size, reported for each dataset is the one with the highest F-score achieved with EVO.

Furthermore, for this alignment size a broader range of different k values were tested. As it can be seen in Table 3, even though a small k (relative to the alignment size) leads to a shorter runtime, it also results in notably lower quality scores for the computed WGAs. In particular, the TC score is more than 8% lower for k = 3 in comparison to the values achieved with k > 10. We also noted that when k becomes large enough, the difference between quality scores become negligible.

Table 3.

Evaluation of WGAs generated by GPA based on simulated WGAs with several different parameters k for the maximal merge size

80 strains	Runtime	PC score	F-score	F-score	TC score	TC score
k	[min.]		GPA with EVO	GPA with PM	GPA in PM	GPA in EVO
3	24	88.03%	0.942	0.947	55.40%	61.46%
7	34	90.38%	0.955	0.961	59.02%	64.90%
12	96	94.35%	0.976	0.982	62.29%	69.61%
17	163	94.70%	0.977	0.983	63.67%	70.68%
22	177	94.53%	0.977	0.984	63.55%	70.62%

Note: All WGAs were evaluated with respect to their runtime (wall-clock time) and PC score. In addition, TC score and F-scores between GPA and EVO as well as GPA and progressiveMauve are reported.

3.2 Evaluation based on biological data: runtime

Since in the current implementation of GPA, we use progressiveMauve as underlying multiple genome alignment method, our evaluation focuses on the direct comparison between the WGA produced by applying progressiveMauve to all genomes at once and the WGA computed using our iterative merging approach implemented in GPA.

To compare the runtimes for the WGA construction of both progressiveMauve and GPA, all WGAs are computed from scratch. Here, for datasets with less than 100 genomes, we chose to split these into randomly distributed groups that were of equal size if possible. For all other datasets, we used the guide tree produced by progressiveMauve, to determine the individual merging steps. In addition, for datasets with more than 100 genomes available, we computed several WGAs of different size. Starting at a set of 10 genomes, we subsequently added new genomes to the set for the next larger alignment. This ensures that we can evaluate the progression of the performance of the tools with the increasing number of genomes.

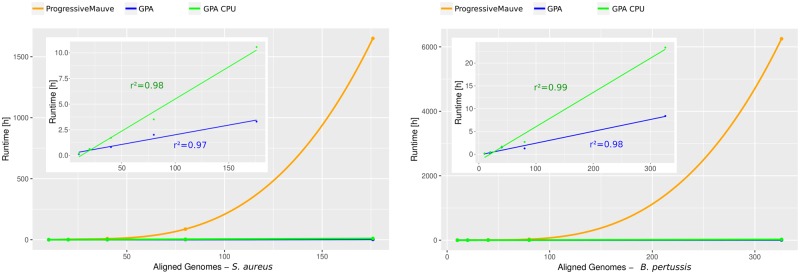
The results (see Table 4) show a general significant runtime decrease for the WGA construction of GPA compared with progressiveMauve, independent of the dataset. As it can be seen from the results and Figure 3, the runtime of progressiveMauve increases at least quadratically with the number of aligned genomes, while for GPA the increase shows a linear dependency.

Table 4.

Comparison between the WGA construction using the original progressiveMauve (PM) method and our SuperGenome-based iterative profile alignment approach of GPA

Dataset			Runtime [min]		No. of LCBs		PC score		TC score	F-score
	Organism	No. of Strains	PM	GPA	PM	GPA	PM	GPA	GPA in PM
		10	27	9	3	6	97.90%	97.97%	93.99%	0.998
		20	98	22	16	4	96.83%	97.29%	88.31%	0.994
	M.tuberculosis	40	475	41	230	72	96.00%	96.61%	85.05%	0.993
	(4.385 Mb)	80	1665	105	852	148	92.36%	93.03%	73.03%	0.990
		128	>350 ha	527	—	437	—	90.67%	—	—
		10	55	25	177	160	38.77%	38.94%	73.13%	0.991
		20	691	90	784	769	41.31%	41.42%	67.18%	0.989
	K.pneumoniae	40	9401	99	3369	1463	42.91%	43.15%	55.94%	0.981
Guide tree	(5.590 Mb)	80	120 038	329	3986	4632	42.15%	42.38%	45.02%	0.974
		166	>6250 ha	771	—	8558	—	41.19%	—	—
		10	16	7	221	53	82.45%	81.81%	73.07%	0.983
		20	64	33	415	362	81.58%	81.11%	67.83%	0.986
	S.aureus	40	552	28	1222	555	76.33%	75.70%	56.63%	0.976
	(2.847 Mb)	80	5213	121	2492	2498	73.02%	72.50%	47.37%	0.976
		176	>1650 ha	198	—	3213	—	71.91%	—	—
		10	24	9	64	56	58.77%	58.99%	95.87%	0.995
		20	99	16	88	115	58.56%	58.45%	90.06%	0.991
	B.pertussis	40	503	96	165	172	57.65%	57.78%	85.48%	0.990
	(4.100 Mb)	80	1683	78	314	373	58.69%	58.39%	75.57%	0.981
		326	>6250 ha	504	—	3708	—	47.37%	—	—
Random
	B.cereus	13	225	61	380	214	60.00%	60.63%	62.40%	0.977
	(5.760 Mb)
	L.monocytogenes	30	628	28	293	254	73.41%	73.92%	61.50%	0.989
	(2.975 Mb)
	C.trachomatis	72	351	14	4	80	98.35%	98.36%	86.68%	0.995
	(1.046 Mb)

Note: The results are divided into two distinct groups, whether for GPA a guide tree (guide tree) was used or not (random). The runtime for WGA computation and the number of LCBs for the respective WGAs is reported. In addition, the WGAs were evaluated with respect to their average PC, the TC score (% of identical aligned columns in PM) and F-score. Both, for the calculation of the TC and F-score, PM is used as the reference. GPA was run with several different parameters k for the merge size, reported for each dataset is the one with the highest PC score.

^aTime past till computation has been manually aborted by us.

Fig. 3.

Comparison of the measured computational runtime needed for the construction of the WGA depending on the number of genomes for the datasets of S. aureus (left) and B. pertussis (right). In addition to the direct comparison between progressiveMauve (orange) and GPA, the upper left section only shows the runtime (wall-clock time) of GPA (blue) and GPA CPU time (green), together with the r² values for the linear regression. The respective regression curves (PM cubic/GPA linear) were computed with R

The scalability and runtime reduction of GPA is most impressive for the WGAs with over 80 genomes. Here, none of the WGAs computed by progressiveMauve have finished after 350 h or even 1650 h (more than 2 months) of computing time, where the choice was made to not further wait for the result. Note in all these cases, the guide tree was still constructed. In contrast to this, GPA could compute all WGA computations within a couple of hours or maximally few days. For example for the WGA of 176 Staphylococcus aureus strains GPA needed slightly more than 3 h (198 min), while progressiveMauve ran more than 1650 h without reporting a result, thus in this case GPA was at least 500 times faster.

Independent from the used WGA construction method, the runtime comparison between the datasets of the species shows differences as well. Here, an essential factor is the average genomic length. The computation time needed for WGAs with the same number of aligned genomes was less for the shorter genomes of S.aureus than for Mycobacterium tuberculosis and B.pertussis, which show comparable average genome lengths as well as runtimes. The WGAs for Klebsiella pneumoniae that has on average the longest genomes also needed the longest absolute runtime. When comparing the results of M.tuberculosis and B.pertussis, which have a similar length, the diversity of the genomes within a dataset (reflected by a smaller overall PC score) does not affect the runtime as much as the genome length.

The number of LCBs, which represent genomic architectural differences between the genomes, differ a lot between the organisms analyzed here. For example, WGAs of M.tuberculosis and B.pertussis with similar genome lengths have vastly different number of LCBs. On the other hand, as can be seen from Table 4 with increasing number of aligned genomes from the same organism also the number of LCBs always increases, independent whether the WGA was computed using progressiveMauve or GPA. When comparing progressiveMauve and GPA for a given set of genomes, the number of LCBs is largely of similar order of magnitude, though in most cases (but not all) the WGA computed with GPA had less LCBs than those for the WGA computed with the original progressiveMauve.

3.3 Evaluation based on biological data: qualitative comparison of WGAs

In order to compare the WGA computed using GPA with the one computed by the original approach of progressiveMauve, we applied three evaluation criteria (see Section 2). For each dataset, we calculated the average PC score, TC score and F-score (see Table 4). For the calculation of TC and F-score, the progressiveMauve-generated WGA was chosen to be the reference.

For each dataset, independent of the number of aligned strains per species, the average PC score is very similar between the progressiveMauve- and GPA-derived WGAs (<1% difference). The largest difference of 0.67% is observed for the alignment of 80 strains of M.tuberculosis, where GPA yields a slightly higher PC score than progressiveMauve. Overall, the PC only slightly decreases within a species when adding more genomes to the alignment. The largest difference was observed for the WGAs computed for B.pertussis: here the average PC score dropped from 59% for 10 genomes down to 47.4% when 326 genomes were aligned. An exception has been observed for the K.pneumoniae WGAs. Here the average PC score of the WGA built from 10 and 20 genomes was smaller than for the WGAs with 40 and 80 genomes. Generally, the PC score differs most strongly when comparing different bacteria. While the WGAs of M.tuberculosis and Chlamydia trachomatis have average PC scores greater than 90%, the WGAs of K.pneumoniae achieve a maximum of 43%.

The TC score, which represents the fraction of identically aligned columns, compares the WGAs computed by GPA with the one derived with the original progressiveMauve. Overall the TC score is above 60% in most cases, indicating that GPA aligns a majority of all columns identically to the original progressiveMauve even for larger WGAs with up to 80 genomes. Also, none of the WGAs of our test datasets shows a TC score below 45%. Similar to the PC score the TC score differs between different organisms though here the biggest differences are seen when increasing the number of genomes within a species. Interestingly, the PC and TC scores do not necessarily correlate a lot, i.e. WGAs with similar PC scores do not necessarily have similar TC scores. For example, WGAs with low PC scores (as seen for example in the case of B.pertussis) may have higher TC scores than WGAs with high PC scores (e.g. S.aureus).

Another indicator of the high similarity of the WGAs computed with GPA and those computed with progressiveMauve is the very high F-score. Independent of the organism as well as the number of genomes the smallest value is 97.6% and the largest value is 99.8%. Here, in general the precision score is higher than the recall for the resulting F-score (data not shown). We observed that WGAs with a high TC score also have a high F-score. On the other hand, increasing the number of genomes for a WGA generally leads to a significant decrease of the TC score, while this behavior is not observed for the F-score. An example is S.aureus, where the lowest TC score in all comparisons was achieved, while the F-score is still above 0.97.

3.4 Impact of compressing the guide tree

Next, we analyzed the impact of the multifurcation parameter k, which is used to compress the input guide tree. This parameter k reflects the maximal degree of each internal node of the guide tree, which represents the maximal number of profiles or sequences that are merged in a single step during the WGA computation. Clearly, as can be seen from Table 4, the runtime of progressiveMauve increases significantly with increasing number of genomes. Thus, a trade-off between the number of genomes aligned at a time and runtime needs to be considered when choosing k.

For this purpose, for a given initial guide tree on a given set of genomes, we computed WGAs with GPA using different k. For each k, we reported the runtime, PC, TC as well as the F-score. As expected the majority of all cases shows that larger k result in larger runtimes (see Supplementary Table S1). On the other hand, the PC and TC score, as well as the F-score, are not greatly affected by the choice of k, if k is not chosen too small for the dataset, as it can be seen for the simulated WGA of 80 genomes from Table 3. However, the number of LCBs varies, though a clear pattern cannot be deduced. Furthermore, the analysis of the WGAs, where no guide tree was provided for GPA, and therefore equally sized groups were merged, shows that at least for smaller sized WGAs highly similar results to progressiveMauve can be achieved as well (see lower part of Table 4).

4 Discussion

In this article, we introduced GPA, a tool which extends the WGA method progressiveMauve (Darling et al., 2010) by the possibility to align individual genomes or WGAs to a given profile genome alignment. The challenge in the case of profile-based WGA is that genomic rearrangements like translocations and inversions have to be considered and therefore the profile of genome alignments cannot be as easily derived as in typical MSAs. Each individual genome as well as WGA represents its own coordinate system, and one challenge when merging a given WGA with individual genomes or another WGA is the transfer of the individual coordinate systems into a common one. With our SuperGenome data structure, we have introduced a novel concept that allows the extension of a given WGA by further genomes or other WGAs, through a coordinate transfer along a guiding alignment of their profiles. Currently, we use progressiveMauve together with GPA and guarantee to adhere also to the LCBs computed by progressiveMauve.

Clearly, progressiveMauve has been shown to be among the best methods for the alignment of bacterial genomes because of its ability to consider rearrangements between the genomes. However, the runtime of progressiveMauve which was shown to be at least quadratic (Darling et al., 2010), as well as lack of parallelization, prevent the computation of WGAs of hundreds or even thousands of genomes. Thus the second goal of this article was to significantly reduce the runtime of progressiveMauve.

One central feature of progressiveMauve is a binary guide tree and a WGA that is progressively computed along this tree. A large fraction of the runtime of progressiveMauve is dedicated to the optimization of the genomic rearrangements (through repeated reanchoring) of all genomes aligned at the respective node in the guide tree. The key algorithmic ingredient in GPA is the use of a compressed rather than strictly binary guide tree and the adaptation of our introduced profile WGA to the alignment of several profiles in one step. The compressed guide tree leads to a significant reduction of internal nodes and therefore subalignments that are merged at a time. It should be noted, that alignment of genomes/profiles at each node in the guide tree used by GPA is performed with progressiveMauve, which also explains the resulting high quality of the WGA.

Though by definition the SuperGenome can be derived from WGAs of arbitrary species, we have restricted our analyses to intraspecies microbial genomes, i.e. aligning different strains from the same species. For our largest dataset of B.pertussis with 326 genomes, GPA needed <9 h, while a sole progressiveMauve -based alignment was not finished after 6250 h (after which we aborted the computation). A linear regression analysis showed a clear linear relationship between runtime and genomes (see Fig. 3). Based on the coefficients of the regression the computation of a WGA with 1000 S.aureus genomes for example would need about 19 h, a WGA of 1000 B.pertussis genomes about 26 h. It should be noted that GPA always uses a precomputed guide tree. In the runtime comparison, the computation for the guide tree in progressiveMauve was not subtracted from the overall runtime. However, this part of the complete runtime in most cases is negligible (<10%, see Supplementary Table S2). Only for the WGA of K.pneumoniae, the fraction of the guide tree computation for the small number of genomes (10, 20, 40) was larger than 50%. For the practical application of GPA, we recommend Parsnp, which for example was capable to produce the guide tree for the 326 genomes of B.pertussis in <20 min.

The results of GPA depend on the guide tree and the number of profiles that are merged at each node, our parameter k. As the guide tree determines the order in which the genomes are subsequently added, it is only plausible that the quality of the final WGA decreases if the tree does not reflect their phylogenetic relationship.

The comparison of progressiveMauve and GPA shows that as a trade-off for the reduced runtime of GPA the quality of the WGAs is in most of the cases slightly worse. However, the small differences of the PC scores by only a few percents together with the high TC and F-scores show that the WGAs computed with GPA are highly similar to those computed using the original progressiveMauve approach. In addition, the comparison and evaluation of the simulated data show, that when comparing the WGA computed by progressiveMauve and the one computed by GPA with the ‘ground truth’ both the PC score as well as F-score are almost identical independent of the number of genomes in the WGA. This shows that we could introduce a WGA approach that enables a faster computation of WGAs, while achieving a comparable quality, which was our intention.

We also showed that in some cases there is a trade-off between runtime and quality when deciding how many profiles are merged at the same time. The parameter k controls the maximal number of profiles aligned at a time with progressiveMauve. On the other hand, small k results in a short runtime, however, at the cost of an inferior PC and TC score (see Table 3). Since the results of progressiveMauve show that the computation time needed for WGAs with less than 20 genomes is in most cases below 2 h, a k between 10 and 25 is currently our default and recommended value for larger WGAs with more than 50 genomes. Currently, we have no automated way of choosing a k that optimizes the PC score, however, if k is not chosen too small, the variations between the resulting WGAs are minor. In addition, the generation of WGAs with thousands of genomes by GPA benefits from the usage of large cluster systems, because the independent alignments can be computed in parallel.

Currently, GPA makes use of progressiveMauve as the underlying WGA method, however, the modular implementation allows in principle the support of other WGA methods. Since the SuperGenome data structure requires a one-to-one mapping between the nucleotides of the genomes, only methods are feasible that generate alignments with this feature. The disadvantage of these type of methods, which include progressiveMauve, is that duplicated regions cannot be aligned.

In the current version, memory consumption is an issue of GPA, since the complete SuperGenome data structure is kept in memory to speed up computation. For example, for the alignment of 326 B.pertussis strains, GPA needed between 70 and 110 GB RAM, depending on the parameter k. With the next release, we will introduce an index file for the SuperGenome data structure that is accessed on demand to enable even larger WGAs with significantly less memory requirements. First results indicate that for WGA with more than 100 genomes only a 10th of the RAM used with the original data structure (less than 10 GB for all tested WGAs) is needed (data not shown).

The current version of GPA and the SuperGenome data structure uses the consensus sequence derived from the profiles of WGAs, which we used as a simple solution to efficiently align several profiles. Apparently, this is a feasible, but not an optimal solution, and therefore other methods that use a more sophisticated representation of the profiles for the merging step will be considered as possibly improved solutions in a future release. Furthermore, considering recent efforts with respect to the computation of optimal LCBs and their ordering (Gärtner et al., 2018), which influence the structure of the coordinate system, could further improve our approach.

A possible application of GPA can be seen from comparative genome analyses that rely on a WGA. An example is AureoWiki (Fuchs et al., 2017) (http://aureowiki.med.uni-greifswald.de/), a database of 32 different S.aureus strains that has been built from the results of a WGA-based pan-genome computation. To incorporate new S.aureus strains into the database, would require a WGA with the new genomic sequences. Computing this WGA from scratch could introduce changes that are not consistent with prior results. Here, the profile-based extension of the WGA by GPA preserves the former WGA and allows the addition of new strains without the necessity to completely rebuild the database.

As a conclusion, GPA introduces a time efficient computation of large-scale WGAs through the usage of WGA-profile alignments and adds further utility by the possibility to extend existing WGAs. With GPA hundreds to thousands or more bacterial genomes can now be fully aligned in an acceptable time.

Conflict of Interest: none declared.