Figure 2. Properties of pLI.

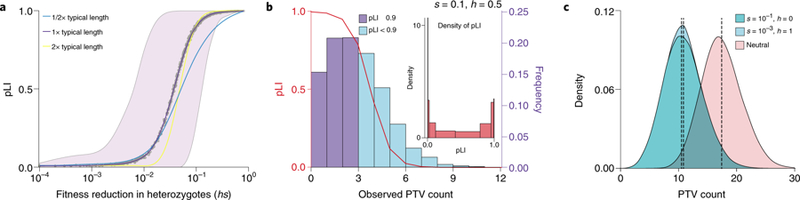
(A) Behavior of pLI as a function of hs. We simulated the counts of PTVs for a range of hs values under a plausible model of population size changes (Schiffels-Durbin model⁴⁷, see Supplementary Note). For each run, we calculated pLI using the observed number of PTVs and the expected number obtained from averaging over neutral simulations. The purple line is the loess smoothed curve over all simulations for each value of hs (the x-axis on a log₁₀ scale), in a human gene of typical length. The shaded area represents the central 95%-tile interval of pLI scores for each value of hs. The cyan and yellow lines are the loess smoothed curves for simulations in a gene with half or twice the length of a typical gene, respectively. (B) For a given hs, pLI scores are highly variable. The red curve depicts the pLI score as a function of the number of observed PTVs. The histogram represents the distribution of simulated PTV counts for s=0.1, h=0.5 under a plausible demographic model for Europeans⁴⁷, in a human gene of typical length; darker bars indicate scores that would be classified as “extremely loss-of-function intolerant”²⁷. The inset shows the density of pLI scores. (C) Complete recessivity (h=0) can lead to similar PTV counts as weak selection on heterozygotes (hs>0). The distribution labeled “neutral” shows the simulated counts of PTVs with h and s both equal to 0. Each distribution shows the results from 10⁶ simulations. Dashed lines indicate the mean of each distribution.