Figure 5.

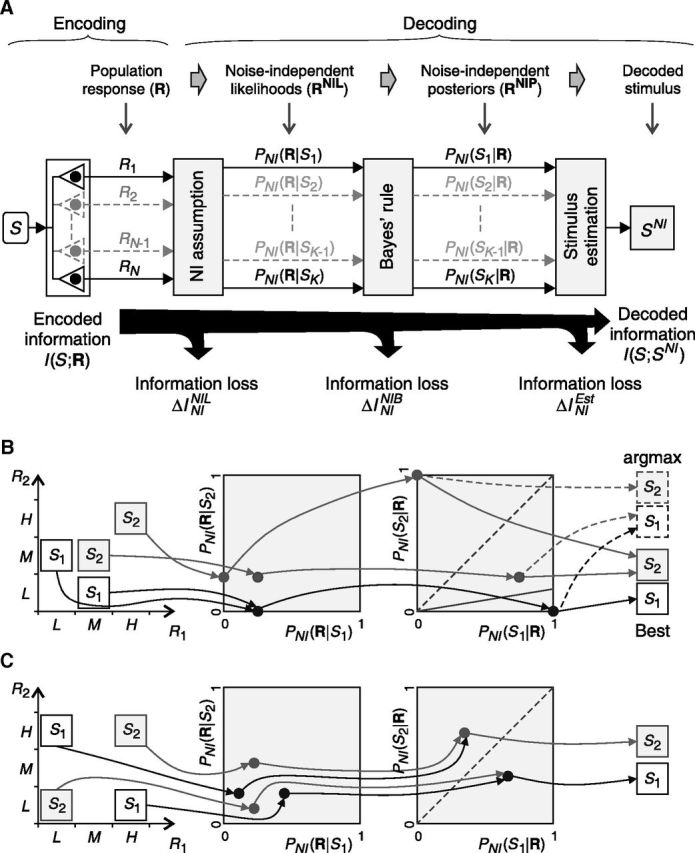
The impact of the choice of a NI decoder. A, The classical NI decoder is modeled as a three-stage process involving: the NI assumption (first stage), in which the population response is transformed into a vector of NI likelihoods (R^NIL); Bayes' rule (second stage), in which R^NIL is transformed into a vector of NI posteriors (R^NIP); and the estimation criterion (third stage), in which the decoded stimulus is inferred from R^NIP. Each stage may induce an information loss. B, C, Population responses of Figure 4, A and C, decoded with the classical NI decoder. B, Both R^NIL and R^NIP keep responses elicited by different stimuli segregated and therefore all information is preserved. However, the stimulus cannot always be correctly inferred by simply choosing the one corresponding to the maximum NI posterior (argmax criterion, dotted line, and arrows; right). Nevertheless, there is an estimation criterion capable of correctly estimating the stimulus (continuous lines and arrows; right). C, Although the NI assumption preserves all the encoded information, after Bayes' rule, responses associated with different stimuli are merged, and thus some (but not all) information is lost (ΔI_NI^NIB is greater than zero). As a result, no estimation criterion is capable of perfectly decoding the stimulus. However, other NI decoders may still be optimal for decoding (Fig. 4C).