Figure 3.

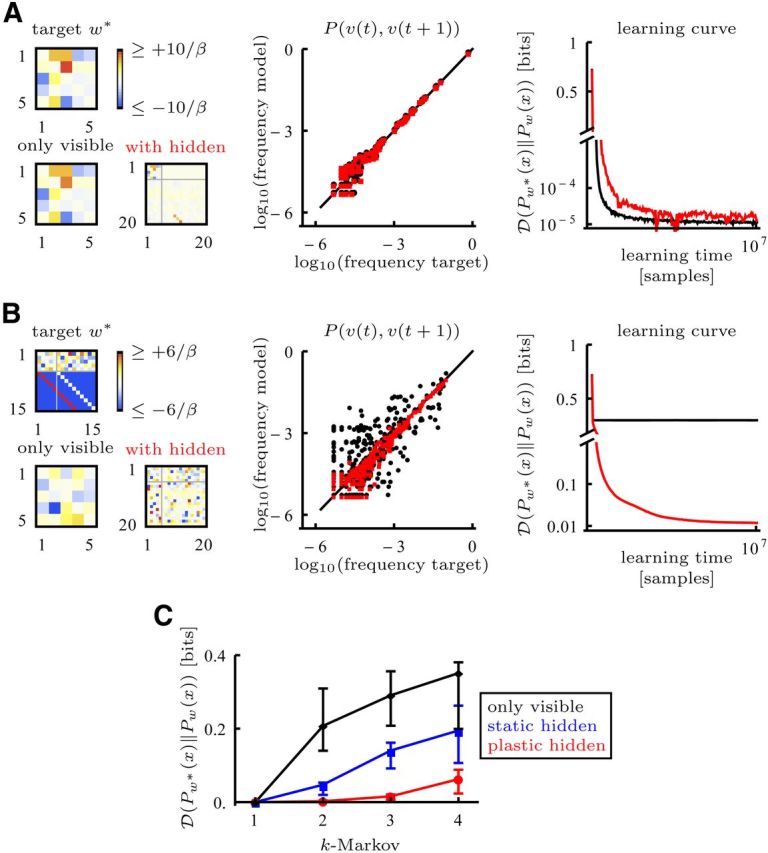
Stochastic targets learned with McCulloch-Pitts dynamics. In all the simulations the target distribution was parameterized by target weights w*. A, Left, For a Markovian target with only visible neurons (k = 1) the weights can be learned with a model with only visible neurons or a model with visible (1–5) and hidden (6–20) neurons (upper left submatrix: visible to visible connections). Middle, Empirical frequency of subsequent activity patterns v(t) and v(t + 1). For dots on the black line the model frequency matches the target frequency. (black, only visible; red, with hidden) Right, The learning curve is similar for both models. B, A k = 3 target cannot be accurately learned with only visible neurons but can be learned with a model that includes hidden neurons. The target was implemented with connectivities such that the first group of hidden neurons (6–10) receives strong excitatory input from the visible and the second group of hidden neurons (11–15) receives strong excitatory input from the first group of hidden neurons. The learned hidden weights do not need to be the same as the target weights. C, With increasing complexity (k = 1 to k = 4) a model with only visible neurons (black) or static hidden weights (blue) is not sufficient to accurately learn the target. The static hidden weights were obtained by reshuffling the weights learned in a simulation with plastic hidden weights. A model with 15 plastic hidden neurons (red) performs well up to the capacity limit k = 4. Learning stopped after 10⁷ target samples, even when learning did not converge. Dots indicate the median, error bars indicate the first and third quartile of the results from 16 simulations with different targets.