Perceptual Inference Predicts Contextual Modulations of Sensory Responses

Abstract

Sensory receptive fields (RFs) vary as a function of stimulus properties and measurement methods. Previous stimuli or surrounding stimuli facilitate, suppress, or change the selectivity of sensory neurons' responses. Here, we propose that these spatiotemporal contextual dependencies are signatures of efficient perceptual inference and can be explained by a single neural mechanism, input targeted divisive inhibition. To respond both selectively and reliably, sensory neurons should behave as active predictors rather than passive filters. In particular, they should remove input they can predict (“explain away”) from the synaptic inputs to all other neurons. This implies that RFs are constantly and dynamically reshaped by the spatial and temporal context, while the true selectivity of sensory neurons resides in their “predictive field.” This approach motivates a reinvestigation of sensory representations and particularly the role and specificity of surround suppression and adaptation in sensory areas.

Introduction

The receptive field (RF) refers to the region in stimulus space that can increase or suppress the spontaneous activity of a sensory neuron (Sherrington, 1906). A simple model of sensory neurons as summing inputs with weights described by the shape of their receptive field has been seminal for our understanding of sensory processing (Hubel and Wiesel, 1962; Aertsen and Johannesma, 1981; Ito, 1985).

However, receptive fields are not invariant but depend drastically on which measurement methods and stimuli are used (Theunissen et al., 2000; Blake and Merzenich, 2002; Carandini et al., 2005), on stimulus strength (Moore et al., 1999; Sceniak et al., 1999; Sutter, 2000; Solomon et al., 2006;), and on stimuli outside the receptive field that do not elicit responses by themselves (Blakemore and Tobin, 1972; Maffei and Fiorentini, 1976; Sillito et al., 1995; Brosch and Schreiner, 1997; Geffen et al., 2007). This non-invariance is due to a collection of nonlinear effects including adaptation (Dragoi et al., 2000; Schwartz et al., 2007), divisive inhibition (Carandini and Heeger, 1994), saliency effects (Sillito et al., 1995), surround suppression (Brosch and Schreiner, 1997; Freeman et al., 2001), and surround facilitation (Polat et al., 1998). As a result, the responses of many sensory neurons to their natural input are not well predicted by their receptive fields (Theunissen et al., 2000; Blake and Merzenich, 2002; Machens et al., 2004).

One possible strategy to solve this problem is to construct more complex descriptive models, introducing nonlinear input and output transformations (Chichilnisky, 2001; Ahrens et al., 2008), lateral connections (Somers et al., 1998), or divisive normalization (Heeger, 1992; Carandini and Heeger, 1994). In contrast, our goal here is to gain a conceptual, functional understanding of these effects as part of what is expected from any sensory system analyzing the sensory scene on-line. We therefore consider sensory processing as an inference problem: given the noisy sensory and neuronal signals, the brain estimates which events and objects caused these observations (von Helmholtz, 1856). While this perspective has been successfully applied on a systems level (Knill and Richards, 1996), its implications on a neuronal level are still the subject of intense research.

Hence, we construct a minimal model of sensory processing where spiking neurons infer which events in the external world caused the sensory input. Each model neuron signals the presence of an “object” that can appear and disappear over time. Each object causes a specific input pattern, e.g., specific sounds cause patterns of cochlear hair cell activation, and visual edges evoke activity patterns in retinal ganglion cells. We propose that neurons can be described by their “predictive field,” the specific input pattern caused by the corresponding elementary object.

Because similar objects can cause similar input patterns, sensory neurons in a network should compete to infer which objects are present in a sensory scene. Ideally, this competition realizes a specific form of divisive inhibition where each neuron selectively shunts the inputs to other neurons with similar predictive fields. Such competition predicts that the receptive field might differ from the cells predictive field and accounts for many puzzling effects, including dynamic RF changes and modulation by the surround.

These phenomena can thus be interpreted as signatures of efficient perceptual inference: they reflect the fact that perceptual inference is a collective result of dynamic competition rather than pattern-matching by independent cells.

Materials and Methods

The first subsection of Materials and Methods introduces the model and describes its dynamics in intuitive terms. The second subsection provides details of the simulations reported in Results. The third subsection provides a more formal description of the model including mathematical derivations.

Intuitive description of the model

One of the most important roles of perception is to interpret a complex sensory scene in terms of the external events that are responsible for it. For example, the visual scene at a busy crossroads is composed of objects such as different people and cars. Interpretation of such dynamic sensory scenes is difficult because of sensory noise, ambiguities such as similarity or occlusions between objects, but also constant changes in the composition of the scene, with people and cars appearing and disappearing in rapid succession.

Sensory neurons selective for much simpler sensory events, such as local contours or elementary sound features, do not face less of a challenge. Their input is noisy, inherently ambiguous, and varies over time. As a result, it is rarely possible to find a unique interpretation of the scene in terms of a particular combination of objects. Rather than trying to find such a single interpretation, it might be more valuable to infer which objects are likely to be present at any given time.

We can formalize this as an instance of probabilistic inference. The perceptual interpretation of a sensory scene implies inferring the external events X responsible for the sensory input S. The likelihood P(S|X) expresses the fact that the sensory inputs caused by these underlying events are potentially corrupted by noise or are inherently ambiguous due to the underlying physics.

P(S|X) together with the prior probability of sensory events P(X) forms a generative model (GM) that allows predicting sensory inputs. The role of perceptual inference is to compute the posterior probability P(X|S), e.g., to infer from the input S which objects X are currently present. In other words, sensory processing approximately inverts the GM using the Bayes rule, i.e., P(X|S) = P(S|X)P(X)/Σ_X' P(S|X')P(X').

Sensory statistics and network structure.

Some simple assumptions about the origin of sensory inputs are schematized in Figure 1a. We here give a brief intuitive description and further details can be found in the subsection Formal description of the model.

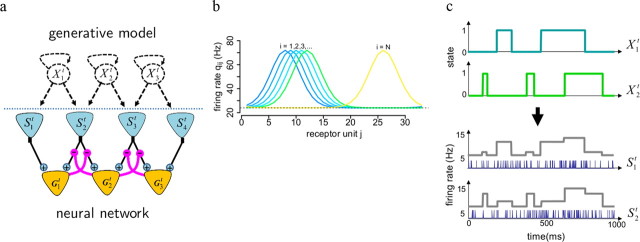
Figure 1.

The generative model and its neural implementation. a, Relation between GM and neural network. The dashed circular units represent objects composing the sensory scene, and dashed loopy arrows indicate their stochastic “on” and “off” transitions. Straight dashed arrows indicate that these objects modulate in turn the firing rate of receptor neurons (blue triangles) producing spike trains (observations) S_j. The neural network (below the dashed line) is composed of the receptor neurons (input layer) and detector neurons (output layer, represented by orange triangles). Detector neurons process their inputs using feedforward (black) and inhibitory lateral (magenta) connections. Lateral connections modulate the gains of feedforward connections (magenta circles) and thus regulate the flow of information between the two layers. b, Predictive fields q_ij used as a simplified model of object structure. Each colored line represents the profile of increased firing rate of receptor units caused by one object (color coded). c, An example illustrating how different objects cause correlated and noisy receptor responses. Two objects X₁ and X₂ appearing and disappearing over time (top two panels) both influence the time-dependent firing rates (i.e., the probability of firing) of two receptor units S₁ and S₂ (bottom two panels, plain lines). While the presence of X₁ has a stronger impact on S₁ (i.e., q₁₁ > q₁₂), X₂ has a stronger impact on S₂ (i.e., q₂₂ > q₂₁). Spikes from S₁ and S₂ (blue vertical lines) are samples from these rates.

The sensory scene is determined by a set of objects, and we model their presence or absence with binary variables (X_i^t), represented by the dashed circular nodes in Figure 1a. These variables take state 1 when the corresponding object is present at time t, and 0 otherwise. Objects can appear and disappear randomly, i.e., their states can switch from 1 to 0 or from 0 to 1 at any time, with a small probability. This is schematized by curved dashed arrows in Figure 1a. The resulting form of stimulus history is illustrated in Figure 1c, top, and allows the model to capture the temporal correlations found in natural sensory stimulation.

The effect of an object on the sensory input is given by the corresponding predictive field, i.e., how its presence (X_i^t = 1) changes the activity of sensory receptors (dashed arrows from X_i^t to S_j^t in Fig. 1a). The receptor units S_j^t produce noisy spike trains with a baseline firing rate q_0j and respond to the presence of each sensory object by a firing rate increase of q_ij (Fig. 1b,c). We will also refer to the S_j^t as the features (i.e., elementary components) of objects X_i^t. “Features” and “objects” thus refer to different levels in the representational hierarchy. For illustration purposes, we assumed that predictive fields have the shape of overlapping circular Gaussian “blobs” (Fig. 1b). The presence of an object activates a set of (here: neighboring) receptors, resulting in spatially correlated elevation of firing rates for receptor units. These signal correlations between responses of cells, e.g., with similar tuning properties, stem from to the sensory stimulus (see below). In early sensory processing, such predictive fields may capture the local correlations observed in various feature spaces, e.g., the spatial extent of luminance, motion, or orientation correlations in natural images, costimulation of whiskers in rodents, or spectrotemporal correlations in sounds. To give a concrete example, “neighboring” objects could correspond to visual bar patterns at the same location but with slightly different orientations. The presence of each such bar typically results in (“predicts”) a correlated pattern of receptor activity, and the closer the orientations of two such bars are, the more their predictive fields overlap. At later processing stages, these predictive fields could correspond to combinations of features defining what we are more used to think of as an object, e.g., a cylinder and a handle for a cup or formants for a phoneme. Overlap between predictive fields reflects the fact that similar objects share many of their low level features.

In Figure 1a, dashed circular nodes and arrows above the horizontal dashed line represent assumptions about the underlying causes of the natural sensory input. In contrast, the plain triangular units and connections below the dashed line represent a neural network. Here, we assumed that each sensory neuron is selective to a particular object in the sensory scene. Thus, the task of model neurons in the detector layer (orange triangles) is to infer on-line which objects are currently present, based on the inputs from the receptors (blue triangles). Since each neuron corresponds to one object, we will also refer to q_ij as the predictive field of the detector specialized for object X_i, or, in short-cut notation, detector i. Feedforward excitatory connections from receptors j to a detector i (black connections) pool inputs from its predictive field, i.e., from the subset of receptors whose activity is influenced by its preferred object. The neural network also requires inhibitory lateral connections between different object detectors (magenta connections). They modulate the feedforward inputs and perform “explaining away” (see below).

Note that the role of sensory “receptors” and object “detectors” is not bound to a specific stage of sensory processing. The dynamics of spike generation in detector neurons ensure that output spike trains can be processed as inputs by the next layer (Denève, 2008). For example, retinal ganglion cells could correspond to receptors and LGN neurons to object detectors. At the next stage, LGN neurons now stand for receptors and V1 cells for object detectors. This network structure represents one layer in the hierarchical and compositional structure of the sensory world and its counterpart in the brain.

Neural network dynamics and divisive inhibition.

Detecting objects from model receptor responses is difficult for three reasons: (1) The sensory input is noisy: while receptors' firing rates are determined by the objects in the scene, spike timing and spike counts fluctuate from trial to trial (Fig. 1b,c). (2) The visual scene can change over time, i.e., objects appear and disappear randomly. (3) Similar objects will activate similar sets of receptors (Fig. 1b), and different configurations of objects might induce similar activation patterns (note that several arrows from different objects X_i^t point to the same observable S_j^t in Fig. 1a). Such ambiguities are unavoidable. For example, many 3D objects project exactly the same image on the retina. Solving these ambiguities requires the use of additional knowledge, e.g., implemented by the prior probability of object appearance.

Due to these ambiguities and the noise, it will not be possible to decipher the composition of the scene with absolute certainty. All a detector can compute is an estimate of whether its preferred object is present or not, e.g., the probability of presence of the object i at time t, p_i^t. We can reexpress this probability as the log odds ratio L_i^t = log p_i^t/1−p_i^t. This results in the following approximate inference equations (see Derivation of input targeted divisive inhibition, below):

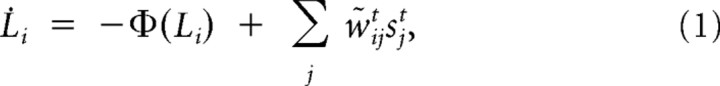where Φ(L_i) is a leak term (see Formal description of the model) and s_j^t is the spike train from receptor neuron j. The w̃_ij^ts can be interpreted as time-dependent effective synaptic weights. These effective feedforward weights implement an approximation to the otherwise computationally intensive inference process and are given by the following:

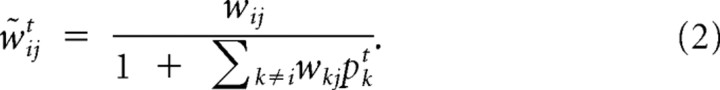w_ij = $\log \frac{q_0+q_{ij}}{q_0}$ is the default (fixed) weight of the synaptic feedforward connection from receptor neuron j to detector neuron i. Thus, the input from receptor neuron j to detector neuron i is modulated by the on-line prediction from all other detector neurons for this input channel.

Thanks to this input-targeted divisive inhibition (DI), even detectors that share most of their inputs nevertheless code for independent objects and have decorrelated responses (see Results).

The equations above are derived entirely from approximate inference. This is a normative model describing how the objects described by the GM can be detected efficiently. It contains no free parameters and is self-sufficient. All contextual effects reported in Results are a direct consequence of the gain modulation of the effective feedforward weights w̃_ij^t by the prediction from other detectors. The contextual modulations predicted by perceptual inference are thus largely independent from their specific neural implementation (see Discussion).

However, to generate predictions for sensory neural responses, we need to specify how probabilities are represented by detector units. We used a previous model (Denève, 2008) based on the principle of self-consistency, i.e., on the unique constraint that output spike trains can be processed as inputs by the next processing stage (i.e., detectors can be considered as receptors by the next layer). Briefly, each detector neuron i accumulates sensory evidence for its corresponding object by means of a leaky integration of input current Σ_jw̃_ij^ts_j^t. An output spike is fired when its membrane potential (the integrated sensory evidence) reaches a threshold η/2, followed by a reset to −η/2. This firing mechanism ensures that that postsynaptic integration of its output spikes (e.g., performed by a postsynaptic neuron) approximately recovers the probability of presence of object i, i.e., that G_i^t ≈ L_i^t with the following:

Φ(G_i) is a leak term as in Equation 1 (see Formal description of the model) and o_i(t) represents the output spike train of neuron i. To get local neural update equations, we used postsynaptic integration of output spike trains from detector neurons to modulate the effective synaptic weights through lateral connections, i.e., we replaced p_k^t by $\frac{e^{G_k^t}}{1+e^{G_k^t}}$ in Equation 2. The weighted suppressive impacts w_kjp_k^t could correspond, for example, to the amount of neurotransmitter released by an inhibitory synapse connecting neuron k to the presynaptic terminals of receptor j. The only free parameter of the model is η. It regulates how many output spikes are fired but has no other impact on the results reported here.

Alternative models for lateral competition.

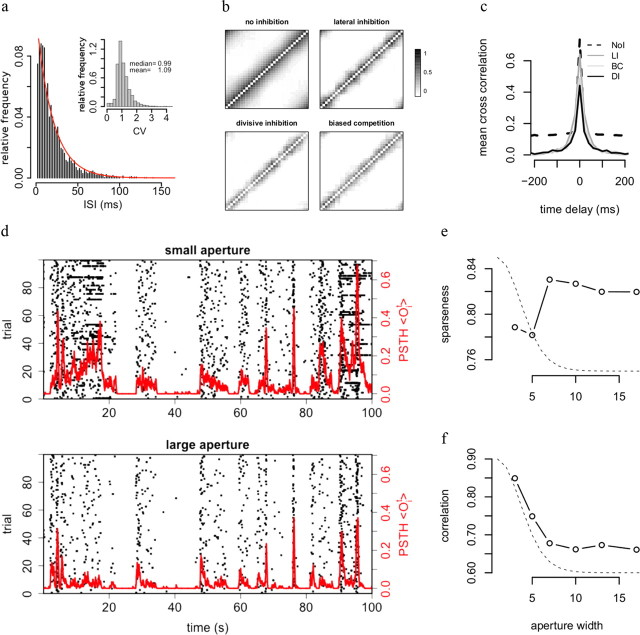
Other forms of competition have been proposed previously to perform redundancy reduction. For example, subtractive lateral inhibition (LI) corresponds to subtracting from the input a prediction of this input by other detectors (Srinivasan et al., 1982). Similar mechanisms are implemented by sparse coding (Olshausen and Field, 2004; Rozell et al., 2008) or by feedback connections in predictive coding (Rao and Ballard, 1999; Spratling, 2010). In our framework, LI consists in replacing the gain modulated input to detector i, i.e., Σ_jw̃_ij^ts_j^t by nonmodulated feedforward inputs and inhibition from lateral connections, Σ_jw_ijs_j^t − Σ_k≠jΦ_kjp_k^t, where Φ_kj = Σ_iw_ikq_ik (see Formal description of the model).

More recently, Spratling (2008) proposed predictive coding as a model of divisive biased competition (BC). In this model, a prediction from the detector layer is used to divide the input from the receptor layer. As shown in the formal description of our model, the DI network can be transformed into a biased competition network by replacing the effective weights in Equation 2 by w̃_ij^t = $\frac{w_{ij}}{1+{\Sigma }_k{w}_{kj}{p}_k^t}$, i.e., replacing “k ≠ i” by “k” in Equation 2. Thus, when p_k^t is small because there is not enough information in the sensory input to precisely discriminate between objects, the difference between the two models vanishes. Despite their strong similarity, however, BC performs significantly worse than DI when multiple objects are present in the scene (see Results, Divisive inhibition improves detection performance).

Simulation protocol

If not mentioned otherwise, all simulations were performed with a network of I = 33 receptor (input) units and J = 33 detector (output) units, using Δt = 0.002 s. Other parameters were η = 1, γ_i = 1, q₀ = 24 Hz. The predictive fields specified by the q_ij were circular Gaussians (von Mises functions) described by q_ij = 48 exp $\left(\frac{\cos \left(\frac{2\pi }{N}\left(j-i\right)\right)-1}{\alpha }\right)$ Hz with α = 0.25. This is a natural choice for periodic feature spaces like orientation or movement direction and helps to avoid numerical artifacts due to boundary effects. Individual objects were assumed to switch on and off with rates r_i^on = 0.2 Hz and r_i^off = 2 Hz.

Measuring model performance.

Input targeted divisive inhibition in Equation 2 represents an approximation (see Formal description of the model). Exact inference would require computing the probability of all possible 2^N object configurations. This is computationally intractable, even in our simple toy model with only 33 objects. To measure the performance of the model and illustrate the importance of selective divisive inhibition, we generated 200 small generative models (I = 7, J = 5). We picked the transition rates r_i^on and r_i^off from uniform distributions between 0.2 and 0.4 Hz and 0.32 and 0.8 Hz, respectively. Baseline firing rate was chosen uniformly with q₀ ∈ [8, 32]Hz and the q_ij were randomly scaled circular Gaussians (see above) with α = 0.5 and maximal height q^max ∈ [40, 60]Hz.

The network models with divisive inhibition perform inference as described in Equations 2, 3, and 5. We compared their performance to networks without divisive inhibition (NoI), networks with LI, and with biased competition (BC). The NoI use Equations 3 and 5 but replace the effective synaptic weights w̃_ij by the fixed feedforward weights w_ij.

As a measure of decoding performance, we used the log likelihood per time bin Σ_tlogP(s^t | X̂^t)/N of the inferred sequence X̂^t. This quantifies how probable the observed receptor spike trains are given the inferred state sequence of length N, and, therefore, how well the inferred sequence predicts (reconstructs) the receptor inputs.

Performance of these networks was compared with the performance of exact inference. Exact inference uses the forward step of the Baum Welch algorithm (Rabiner, 1989), grouping all objects into a single HMM whose hidden states correspond to the 2^N possible object configurations. Posterior probabilities p_i^t are obtained by marginalizing over all configurations where object i is present.

To see whether the results are representative of larger networks, we also measured the performance of networks for larger generative models, as described previously (I = J = 33). For simulations with these bigger GMs, exact inference is intractable but we know the true state sequence that generated the receptor inputs. We therefore used the likelihood of the true sequence rather than the sequence inferred using the Baum Welch algorithm as a reference.

Inferred sequences for the different models are obtained by thresholding the values of the marginal posterior probabilities p_i^t, i.e., X̂_i^t: = H(p_i^T − c) where H( · ) is the Heaviside function and c a constant. c was chosen to optimize decoding performance for each GM and each inference method.

Response of the model to naturalistic and apertured stimuli.

“Naturalistic stimuli” were defined as sequences of inputs generated by the GM, i.e., using HMMs with parameters r_onⁱ, r_offⁱ, q₀, and q_ij to sample the input spike trains of detector units (Eq. 4).

We characterized the variability of the network's output spike trains by measuring the coefficient of variation of detector unit interspike intervals Δt. It was defined as CV : = 〈Δt〉/σ(Δt) where 〈 · 〉 denotes the expected value and σ(·) the SD of the empirical distribution.

To illustrate the decorrelating effect of divisive inhibition, we stimulated the network with 200-s-long sequences of naturalistic stimuli generated by the GM. We then measured correlation coefficients r_ij = cov(O_i^t, O_j^t)/$\sqrt{\mathrm{var}\left(O_i^t\right)\mathrm{var}\left(O_j^t\right)}$ between the output spike trains of unit i and j as well as cross-correlation functions between the spike trains of neighboring units for various time delays τ defined as r_ij(τ) = cov(O_i^t, O_j^t−τ)/$\sqrt{\mathrm{var}\left(O_i^t\right)\mathrm{var}\left(O_j^{t-\tau }\right)}$.

To study the effect of lateral competition on response sparseness and selectivity, we measured the correlation and sparseness of detector unit responses to apertured naturalistic stimuli, a protocol inspired by Vinje and Gallant (2000). Manipulating the aperture size within which the stimulus can be seen changes the number of receptors effectively providing input. Because this also alters the number of detectors receiving this input, it changes the pool of potentially competing units.

To simulate an aperture centered on the receptive field, we used the GM to generate receptor unit activity inside the aperture, but clamped the firing rates of receptor units outside of it to baseline firing rate q₀. The aperture contained the receptor at the center of the predictive field of the recorded neuron, plus two (smallest aperture) to 16 units (corresponding to full field stimulation) on each side. We measured the PSTHs of detector units from 100 repetitions of the same movie, i.e., in response to 100 different input spike trains sampled from the same object sequence. Sparseness was defined as S : = {1 − [(Σr_i/n)²/Σ(r_i²/n)]}/[1 − (1/n)], where r_i is the mean response to the ith frame of a stimulus sequence of length n. More exactly, r_i is the mean number of spikes fired by the unit between t = i to t = i + Δt, averaged over 100 repetitions of the same 200 s object sequence. Values range between 0 and 1, larger values indicating higher sparseness (Vinje and Gallant, 2000).

Mapping the receptive fields of detector units.

We mapped the RF shape of detector units using spike-triggered average (STA) and stimuli similar to “dense noise” (Reid et al., 1997). This type of stimulation was generated by randomly switching individual receptors from “dark” to “light” on a fast timescale and such that on average half of the receptors fired at increased rate. This stimulus that is dense both in the number of activated receptors as well as in time allows us to assess how their input is integrated and helps to reveal potential nonlinear interactions.

Effectively, the stimulus made receptor firing rates switch between a baseline rate q^off = 16 Hz (dark pixels) and an elevated rate q^on = C (light pixels) to create dense noise random checkerboard stimuli. Contrast ranged from C = 40 Hz (low contrast) to C = 80 Hz (high contrast). This contrast manipulates the SNR in the input, given by (q^on − q^off)/q^off. Individual receptor units switched from dark to light and light to dark with a rate of 4 Hz, i.e., much quicker than the assumed object timescales. The STA of a detector unit was finally determined by averaging the receptor units' spike trains at various delays before each output spike fired by this detector unit, during 200 s of dense noise stimulation.

We also mapped the receptive fields of detector units with stimuli of increasing width. To generate stimuli of increasing sizes, we activated units in an increasingly larger portion of the receptor layer, starting from the center of the unit's predictive field. Thus, a stimulus size of 1 corresponds to activating the central receptor plus the one receptor on the right as well as the one to the left. Inactive receptors stayed at baseline firing rate q₀ = 20 Hz. The firing rates of activated receptors were increased to C, with contrast ranging from C = 50 Hz to C = 100 Hz. Receptive fields of detector units were mapped by plotting the output firing rates as a function of stimulus width. Firing rates were measured as the average spike count during 500 repetitions of 1 s of such stimulation. We will refer to “wide stimulus” and “narrow stimulus” for stimulus width 4 and 1, respectively.

Another commonly used method to measure RF shape is to record the cell's responses as a function of the spatial frequency of the stimulus. To measure frequency tuning of unit i, we switched firing rates of each receptor j from baseline to $q_0+\frac{C}{2}\left[1+\cos \left(f\frac{2\pi }{N}\left(j-i\right)\right)\right]$, were f is the spatial frequency. Average output rates were measured over 500 repetitions of 1 s sinusoidal stimulation

Finally, we used a new adaptive method based on spike-triggered averaging to measure the selectivity of detector units. The method has the advantage of producing estimates much more similar to the unit's true predictive field than the standard STA (see Results). Standard STA uses “white noise” stimuli to produce an RF estimate unbiased by spatiotemporal correlations in the stimulus (Chichilnisky, 2001). Unfortunately, this estimate of the cells selectivity is typically corrupted by competition with other cells. In contrast, the adaptive STA method aims at estimating the stimulus features encoded (predicted) by a cell, untroubled by potential interactions with other units. This is insured by giving as much advantage as possible to the recorded cell in its competition with other units.

More concretely, it consists of the following steps: (1) The standard STA is estimated using dense noise at high contrast (e.g., C = 120 Hz). (2) Together with a constant offset, the STA profile at delay t₁ = 0 (e.g., thick orange lines in the bottom of Fig. 5a or black line in Fig. 7b) forms a background firing rate profile (here: ranging between 20 and 80 Hz). The offset should be chosen such as to yield meaningful input stimuli (e.g., non-negative receptor firing rates or luminance values). (3) The adaptive mapping stimulus is then obtained by adding dense noise to this profile, i.e., at each time step, the firing rates of individual receptors are given by the background profile plus a random increase or decrease (e.g., by 20 Hz), yielding randomly varying receptor firing rates (between 0 and ≈ 100 Hz). The mean-corrected STA using this composite stimulus then yields the adaptive PF estimate. Because the background profile selectively activates the detector under study, effects due to lateral competition from other detectors are reduced. This allows us to get an estimate closer to the detector's true predictive field.

Figure 5.

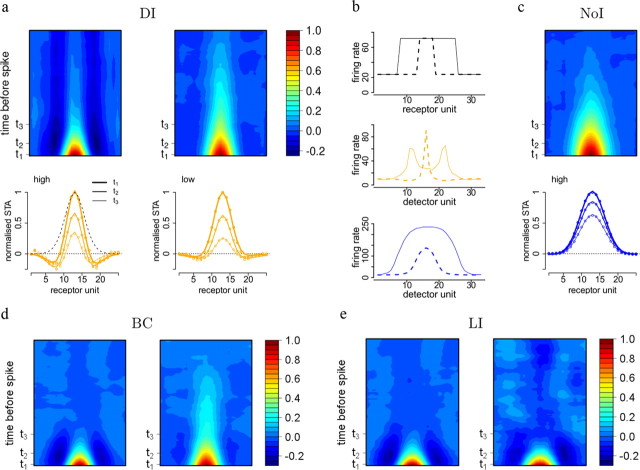
Spike-triggered averages. a, Top row: Normalized and mean-subtracted spatiotemporal STAs resulting for stimulation with dense noise at high contrast (q^on = 80 Hz) and low contrast (q^on = 40 Hz). Bottom row: Temporal modulation of excitatory and inhibitory integration. Lines of different width correspond to sections along the horizontal axis at t₁ = 0, t₂ = 40, and t₃ = 100 ms before spike, as indicated above. b, Cells in the network with DI respond most to salient stimulus aspects. Top row: Activating a subset of receptor units to fire at increased rate (plain line: receptors 8–25, dashed line: receptors 14–18) results in selective responses. Middle row: Network response during stimulus presentation. While a narrow stimulus most strongly excites cells with a predictive field centered on the stimulus, wider stimuli evoke selective responses for cells centered close to the stimulus borders. Bottom row: Networks without divisive inhibition do not show this selectivity due to the lack of competition. c, Spatiotemporal STAs for cells in a network without divisive inhibition at high contrast. d, STAs for cells in a network with BC at high (left) and low contrast (right). e, STAs for cells in a network with LI at high (left) and low contrast (right).

Figure 7.

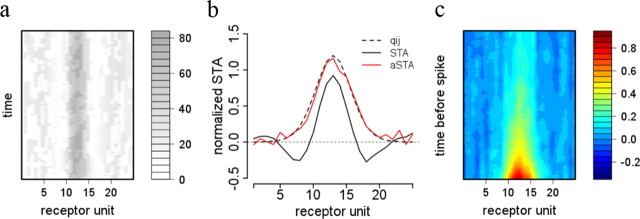
Measuring predictive fields. a, Adapted stimulus superimposing the naive STA and the checkerboard stimulus. Gray value indicates stimulus intensity, details are given in Materials and Methods. b, True predictive field (dashed line), the naive estimate (plain black line) and the estimate resulting from the adapted stimulus (red line). c, Full spatiotemporal STA using the adapted stimulus.

Measuring center-surround interactions.

To illustrate the context dependence of detector units in the network, we tested a detector unit's response while activating different parts of the central receptive field and surround. The central RF corresponded to the input units for which the STA was positive and at least 5% of its maximum value. Here, the STA was measured with the standard method using dense noise stimuli. The surround was defined as the receptor units positions outside this central receptive field. Receptor units were activated by setting their firing rate to 240 Hz. The response of the detector units was measured as the mean rate during presentation of the test stimulus over 250 repetitions of the protocol.

To examine the reshaping of tuning curves by the context we also measured detector unit's responses while activating other detector units. These other detector units were activated by clamping their probability to p_j = 0.999. The resulting changes in receptive fields were determined by measuring the detector unit's response to activation of single receptors at different positions.

Measuring adaptation to previous stimuli.

To simulate the effect of adaptation, we first presented an adapting stimulus at a fixed position a, i.e., we sampled spikes using Equation 4 with X_a^t = 1 and all other X_j^t = 0 from t = 100 to t = 570 ms. Thirty milliseconds after the disappearance of the adaptive stimulus, we presented a single test object for 200 ms at various positions k, i.e., we used Equation 4 with X_k^t = 1 from t = 600 to t = 800 ms. Tuning curves were defined as the mean onset firing rates for 500 repetitions of the test stimulus, as a function of k. The control without adaptation uses the same protocol but without the adapting stimulus, i.e., no objects are presented before the test stimulus.

Formal description of the model

Single units are described by the spiking neuron model introduced by Denève (2008). It is derived from a hidden Markov model (HMM) with binary hidden states X_i^t ϵ {0, 1} and binary observations S_j^t ϵ {0, 1}. X_i^t = 0 and X_i^t = 1 are called the “off-state” and the “on-state,” respectively. For the S_j^t, 0 versus 1 stands for no spike versus a spike from presynaptic neuron j, respectively.

Generative model for receptor activity.

During small time intervals Δt, the probabilities of the state X_i^t to switch from 0 to 1 and vice versa are given by r_i^onΔt = P(X_i^t+Δt = 1|X_i^t = 0) and r_i^offΔt = P(X_i^t+Δt = 0|X_i^t = 1). r_i^on and r_i^off control the rate of appearance and the average duration of the stimulus, respectively.

The probability of observing a spike in channel j in time interval Δt given the configuration X^t := [X₁^t, X₂^t, …, X_M^t] of hidden objects is modeled as a linear superposition, as follows:

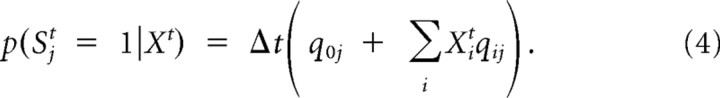where Δt q_ij stands for the probability that object i causes a spike in receptor j in an interval of length Δt. The term Δt q_0j models the effect of unspecified causes such as background noise. In the limit of small Δt, the instantaneous firing rate of receptor j is given by q_0j + Σ_iX_i^tq_ij.

Dynamics of single detector units.

Let us first consider the case when there is no overlap between predictive fields, i.e., each object i affects a distinct set of receptors. In this situation, if q_ij is larger than 0, then q_kj = 0 for all k ≠ i. This situation does not require interactions, and is equivalent to I independent HMMs, one for each object.

Let p_i^t = p(X_i^t = 1|S^(t)) denote the probability of feature i being present at time t given synaptic input S^(t) := [S₁^(t), S₂^(t), …, S_M^(t)] with S_j^(t) := [S_j¹, S_j², …, S_j^t] being the input from receptor units j up to time t. The dynamics of unit i are described via the log odds L_i^t := $\log \frac{p_i^t}{1-p_i^t}$. As a consequence, the probability of feature i being present is a simple function of L_i^t, i.e., p_i^t = [1 + exp(−L_i^t)]⁻¹.

Taking the limit of Δt → 0 for the discrete time HMM yields a continuous process with temporal dynamics L̇_i = $\frac{d}{dt}{L}_i$ given as the following:

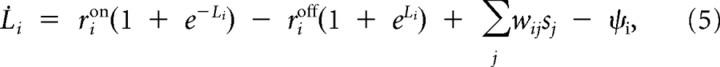where s_j = Σ_k δ(t_jk − t) refers to the input spike train from channel j. A derivation of this result is provided in Denève (2008).

The weights w_ij for incoming spikes and the drift term Ψ_i are given as follows:

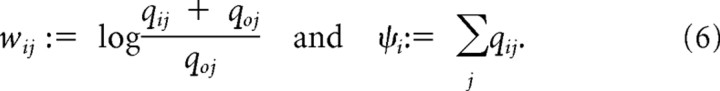Outputs are generated by integrating Equation 5 up to a dynamic threshold G_i whose dynamics read as follows:

where o_i = Σ_kδ(t̃_ik − t) is the output spike train of unit i. The unit is said to fire spikes at times t̃_ik when L_i exceeds G_i by more than η/2 at which point the threshold is increased by η. γ_i is a constant drift term analogous to Ψ_i (Denève, 2008). Using the abbreviation φ_i(G) := −r_i^on (1 + e^−G) + r_i^off (1 + e^G) + γ_i one arrives at Equation 3 for G.

L_i^t estimates the probability of object i being present given the receptor inputs. This is an analog quantity, but it has to be signaled via a binary output spike train O_i^t. The adaptive threshold G_i simulates the dynamics of the internal probability estimate of a putative postsynaptic unit receiving O_i^t as input. Whenever G_i decays too far below the actual probability L_i, unit i fires a new spike such that a putative postsynaptic unit can appropriately update its probability estimate. As a result, the dynamic threshold tracks the probability of presence of the object. η controls the precision of this spike-based representation of probability, and regulates the number of output spikes. Alternatively, this neuron can be understood as an integrate and fire neuron with membrane potential V_i^t corresponding to the “prediction error” V_i^t: = L_i^t − G_i^t. The threshold and reset potential of this integrate and fire unit are η/2 and −η/2, respectively. The advantage of using such spike-based rather than a rate-based representation of probabilities have been described previously (Denève, 2008).

Derivation of input targeted divisive inhibition.

We now extend the previous results to a network that can account for different causes i. Analogous to Equation 6, evidence for object i, observed in channel j (spikes from receptor j), should be weighted by the log ratio of firing rates when the object is present versus absent. In contrast to the case of a single hidden cause, these firing rates now depend on the current presence or absence of all other objects k ≠ i and are given by q_0j + q_ij + Σ_k≠i X_k^tq_kj when object i is present versus q_0j + Σ_k≠i X_k^tq_kj when object i is absent.

Although the true state of the hidden causes is not known to the network, approximate inference can still be implemented via a mean field approach: we use the fact that p̂_i^t: = 1/(1 + e^−G_it) is a good estimate of the posterior probability or expected state p_i^t = 1/(1 + e^−L_it), and replaced the binary X_k^t for all but unit i by their on-line estimate p̂_k^t (cf. Hinton et al., 2006; Bengio et al., 2007). This yields the expected firing rate for channel j when object i is absent versus present as follows:

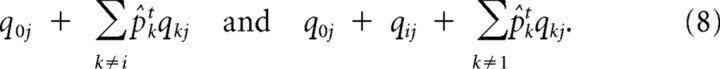With the abbreviation A_ij^t := q_0j + Σ_k≠1p̂_k^tq_kj referring to the influence of causes other than X_i^t, the probabilities of observing NO event in absence versus presence of cause i are

This provides all the information necessary for the inference algorithm and yields the discrete-time multiunit equivalent of Equation 5:

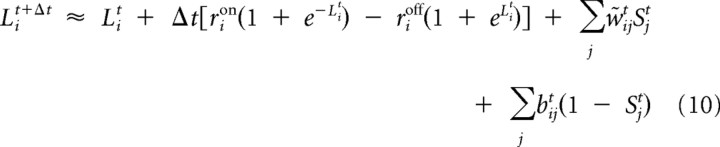with

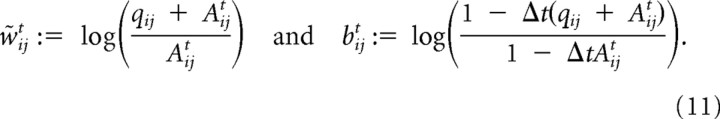In the limit of Δt → 0 Equation 10 gives the continuous equation

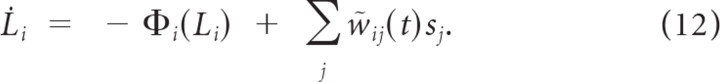The first part of Equation 11 realizes a type of divisive inhibition as can be seen most clearly for q_ij ≪ q_0j, i.e., when input weights are small. We can then use fixed weights w_ij := $\log \frac{q_0+q_{ij}}{q_0}$ and a more standard type of divisive inhibition to approximate the effective weights w̃_ij^t in Equation 12 as w̃_ij^t = $\frac{w_{ij}}{1+{\Sigma }_{k\ne i}{w}_{kj}{\widehat{p}}_k^t}$ yielding Equation 2.

It is important to note that the feedforward weights w_ij are fixed and determined by the parameters of the causal model. The effective weights w̃_ij, however, depend on the network activity and are therefore not static.

Other forms of redundancy reduction.

We compared the performance of input-targeted divisive inhibition with other forms of competition proposed previously as mechanism of redundancy reduction in sensory processing.

In the subtractive LI model, we replaced the feedforward inputs s_j^t in Equation 12 by the prediction errors (s_j^t − A_ij^t). It can be shown that Σ_j w_ij(s_j^t − A_ij^t) = Σ_j w_ijs_j^t − Σ_k≠j Φ_ikp_k(t) − Ψ_i, with Φ_ik = Σ_j w_ijq_kj.

For divisive BC, we replaced Σ_k≠i w_kjp_k^t by Σ_k w_kjp_k^t in Equation 2. Since the gain modulation of the inputs is now independent of the target detector neuron, the feedforward input can be rewritten as Σ_jẇ_ij^tŠ_j^t, with s̃_j^t = $\frac{s_j^t}{1+{\Sigma }_k{w}_{kj}{p}_k^{\mathrm{t·}}}$.

Results

Divisive inhibition improves detection performance

Our model requires a more selective form of interaction than previous models based on lateral subtractive inhibition (Srinivasan et al., 1982), divisive normalization (Shapley and Enroth-Cugell, 1984; Heeger, 1992; Carandini and Heeger, 1994; Schwartz and Simoncelli, 2001), or divisive biased competition (Spratling, 2010). More precisely, connection weights from input receptor and target detectors are selectively shunted by sums of detector responses.

Why should lateral inhibition take this form? We use the toy example illustrated below to provide an intuitive answer in addition to the formal derivation given in Materials and Methods. Consider two neurons selective for similar objects, e.g., a chair and a table as shown in Figure 2a. The presence of a chair or a table typically causes low level features to be present in the visual scene. Some of them are specific, many of them common to both objects. The corresponding detectors have overlapping predictive fields and therefore similar feedforward weights. If they did not compete, the two units would often be coactivated, resulting in false positive responses for either object. For example, the chair unit would often “detect” a chair when instead a table was presented.

Figure 2.

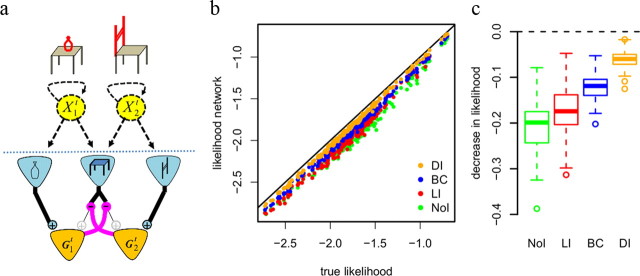
Sensory ambiguity and divisive inhibition. a, Different objects can produce similar sensory responses. For example, a chair and a table share many basic features, such as four legs. Presentation of either a chair or a table will activate receptor units sensitive to these features. To distinguish between the two different objects, the network differentially shunts these common features (magenta connections) thereby enhancing features not predicted by both objects (in red). Effectively, this increases the weight of diagnostic (unambiguous) features. b, Impact of divisive inhibition on decoding performance. Scatterplot shows decoding performance (log likelihood per time bin of the observed spike train given the decoded sequence) of different networks for sequences from 200 randomly parametrized generative models. Orange dots show that networks with DI yield very good decoding performance (horizontal axis shows best obtainable performance using the forward step of the Baum Welch algorithm). Other types of inhibition shown for comparison: NoI, with LI, and BC. c, Performance decrease (difference in log likelihood) for the different models when compared with the forward model.

If the presence of one object explains some of the features in the scene, these same features should not be taken into account for other objects. This phenomenon is called explaining away and well known from studies of inference in causal models (Pearl, 1988). Thus, when the chair neuron is activated, it should prevent the table neuron from responding to features that they have in common but are already accounted for by the presence of the chair (e.g., the four legs). However it should not affect other features (e.g., a bottle) not shared by these objects. Gain modulating the input from receptor i to detector j by the prediction from the other detectors k ≠ j allows the output layer to respond appropriately when only a table, only a chair, or both are present.

As a result of explaining away, receptors that are most important for discrimination will have the strongest impact on the detector units; these receptors encode salient features that are not shared by other objects in the scene (Fig. 2a, highlighted in red). The effective receptive field shapes of the object detectors are not static but shaped by the context.

Input targeted divisive inhibition in Equation 2 represents an approximation. Exact inference would require computing the probability of all possible 2^N object configurations. This is computationally intractable, even in our simple toy model with only 33 objects. To test the performance of this approximation and the importance of divisive inhibition, we sampled different sets of smaller generative models (with randomly chosen parameters) for which exact inference is still an option. We then assessed how well the corresponding neural networks decode the presence of objects (see Materials and Methods).

Figure 2b shows that while most neural networks with DI closely approximate best achievable decoding, NoI perform much worse. Even networks with LI or BC do not achieve the performance of DI (Fig. 2c). This result illustrates the requirement for inhibition to be selective both to the input and the target neuron.

Simulations with larger generative models (e.g., with 33 blob-shaped predictive fields) reproduce the same ordering and confirm that these results generalize to more realistic network sizes (data not shown). The DI network therefore provides a good and scalable approximation to optimal decoding using the forward step of the Baum Welch algorithm (Fig. 2c).

Predicted response properties

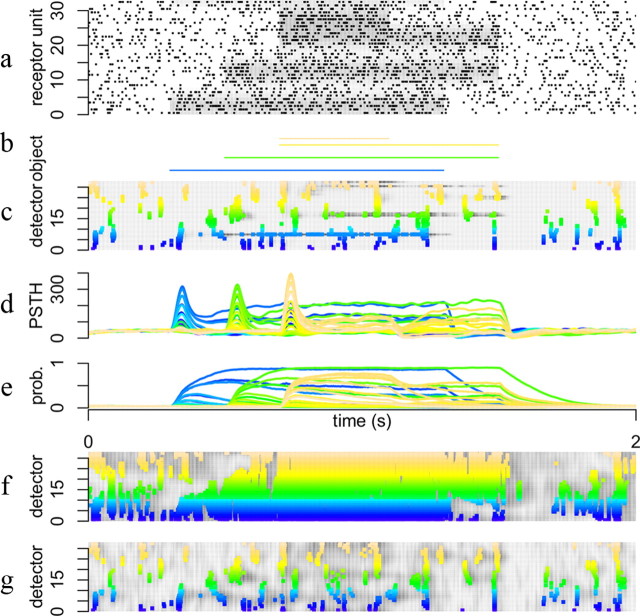
Figure 3 illustrates the typical response properties of receptors and object detectors. In this example, we used the GM with blob-shaped predictive fields as described previously to generate a sequence of four objects (Fig. 3b). These objects locally increase the firing rates of receptors (Fig. 3a, shades of gray). The input to the network, i.e., the spike trains of receptor units, are obtained by sampling spikes from these rates (Fig. 3a, black dots).

Figure 3.

Processing with and without divisive inhibition. a, Raster plot of input spike trains. Firing rates of corresponding receptor units are indicated by shades of gray. b, Presence of objects. Each line corresponds to one out of 33 objects and the presence of 4 objects is indicated by the colored rectangles. The firing rates of the 33 receptor units shown in a were determined by the configuration of objects at each point in time. c, Raster plot of output spike trains from the 33 network units. Gray shading in the background indicates estimated probabilities of the corresponding units and spike color indicates detector unit index. As each detector unit has a RF corresponding to one object in b the colors also indicate preference for the corresponding objects in b. Same color code applies to d–f. d, Poststimulus time histogram indicating estimated firing rates over 500 repetitions. e, Probability of object being present decoded from the output spike trains, averaged over 500 repetitions. f, Raster plot for the network without divisive inhibition. g, Raster plot for the BC network.

In contrast to the receptor units whose firing rates are strongly correlated, the detector units respond sparsely and selectively to their preferred objects (Fig. 3c, colored dots). They do so thanks to input targeted divisive competition (compare Fig. 3c and the network output without divisive inhibition in Fig. 3f). Despite the fact that they share most of their feedforward connections from receptors, their output spike trains code reliably and specifically for the probability of presence of the objects (Fig. 3e). Coactivation of neighboring detectors (Fig. 3e, similar colors) reflects the consequence of noise in the receptors that prevents perfect discrimination between similar objects.

The output firing rates of detector neurons are modulated by the presence of objects but also exhibit additional temporal dynamics (Fig. 3d). Stimulus presentation results in transient, relatively unselective responses of multiple detector units. After the onset, neural activities decay, but at different rates leaving only few detector units active. This response adaptation is reminiscent of transient and sustained responses in the retina (Enroth-Cugell and Robson, 1966), LGN (Butts et al., 2007), and V1 as well as in the somatosensory (Boloori and Stanley, 2006) and auditory pathways (Wehr and Zador, 2003) and is a result of the nonlocal dynamic competition among detector neurons. More precisely, it is due to the interplay between a quasi-instantaneous response to feedforward inputs, due to the detector neurons being activated and reaching their firing threshold shortly after stimulus presentation, and a slower increase of divisive inhibition (Eqs. 2,3) from competing interpretations.

The dynamics of this process illustrate the progressive build-up of a perceptual interpretation of the stimulus (as seen in the slow rises of the probabilities p_k^t in Fig. 3e). The activation of surrounding detectors progressively shunts the feedforward synaptic weights to other units, effectively decreasing their response.

The strength and duration of this competition depends on the number of competing predictive fields and their degree of overlap. Thus, more overlap creates more ambiguities between similar objects and results in stronger competition. For the BC model shown in Figure 3g the competition is slightly stronger, leading to responses similar to DI. The response of the subtractive inhibition model to this stimulus (data not shown) is very similar to BC.

Variability and decorrelation of output spike trains

The output spike trains in response to repeated presentations of the same stimulus are variable from trial to trial. As shown in Figure 4a, the interspike-interval (ISI) distributions of the output spike trains are close to exponential and the coefficients of variation (CV) are ∼1 (inset). This is within the range of observed variability in cortical areas (Tolhurst et al., 1983). Since detector neurons are deterministic, this variability is entirely due to fluctuations in inputs from receptor units. We showed previously that this is expected from single neurons integrating their synaptic inputs efficiently (Denève, 2008), and the implications for neural coding are discussed elsewhere (Lochmann and Denève, 2008). In particular, this code predicts variable responses to static stimuli, but reliable responses to time-varying stimuli (Wehr and Zador, 2003; Boloori and Stanley, 2006; Gur and Snodderly, 2006; Butts et al., 2007).

Figure 4.

Output statistics and cross-correlations. a, ISI distribution of simulated output spike trains is approximately exponential (red line shows exponential fit), yielding CVs close to 1 (inset). b, Correlation matrices of instantaneous output correlations for the network with divisive inhibition and a purely feedforward network without inhibition, and two alternative models of inhibition. In all cases, the network is stimulated with sequences from the true GM. The reduced correlations illustrate the spatially decorrelating effect of inhibition. DI and BC are most effective in reducing correlations. c, Cross-correlation functions for neighboring units illustrating decorrelation in the time domain (see Materials and Methods). Note that LI reduces instantaneous correlations less than DI and BC. d, Poststimulus time histograms (red lines) and raster plots (black dots) for one unit resulting from network stimulation with a small aperture (aperture width = 2, top row) or large aperture (aperture width = 9, bottom row). e, Stimulation with larger aperture increases response sparseness. PSTHs are computed for a cell with RF centered on the aperture as described in Materials and Methods. Dashed line shows shape of the corresponding predictive field. f, Stimulation with larger aperture decreases correlation between the PSTHs of neighboring cells, illustrating decorrelation due to contextual information.

The network performs a form of blind source separation i.e., it infers the separate and independent objects that created the spatially and temporally correlated input. Thus, the responses of different detectors should ideally be independent from each other despite strong correlations in sensory scenes and shared connections between detectors. Indeed, the model network efficiently reduces pairwise correlations between the detectors (Fig. 4b, bottom; c, plain line). Achieving such redundancy reduction requires input targeted inhibition because correlations are much higher for a network without such inhibition (Fig. 4b, top; c, dashed line).

Note that subtractive lateral inhibition and biased competition achieve decorrelation performance similar to input targeted inhibition. This suggests that the better performance of DI is achieved by removing higher order correlations in the sensory scene.

The pairwise correlations shown in Figure 4, b and c, combine “signal correlations,” i.e., slow correlations in detector firing rates caused by objects appearing and disappearing in the scene, and faster “noise correlations,” i.e., synchronous firing of nearby neurons due to shared input noise. They correspond roughly to the tails and central peak of the cross-correlogram in Figure 4c and are both strongly reduced by divisive inhibition.

Perfect redundancy reduction cannot be achieved for two reasons. First, receptors are noisy, resulting in ambiguities between similar objects. Second, resolving these ambiguities takes time: sufficient sensory evidence needs to be integrated to make fine discriminations. As a consequence, correlations at longer time scales are more efficiently reduced than instantaneous cross-correlations between nearby units (Fig. 4c). Finally, redundancy reduction is more efficient when the sensory input is less noisy. Thus, long-term correlations disappear at larger input contrast or signal-to-noise ratio (SNR) q_ij/q₀. Processing at high contrast removes all correlations except a small synchrony due to shared inputs (i.e., the cross-correlogram in Fig. 4c has a single narrow peak at zero). This suggests that the disappearance of long-term correlations in conjunction with persistence of short-term synchrony between pairs of V1 cells for increasing visual contrast (Kohn and Smith, 2005) is a signature of efficient neural inference.

Impact of long range contextual interactions

To illustrate the importance of long-range contextual interactions in ensuring such selective and sparse sensory responses, we compared the detector outputs in response to naturalistic scenes (i.e., scenes generated by the generative model) shown in apertures of varying diameter centered on their predictive field. We asked in particular whether we could reproduce the sparsening and decorrelation of visual responses observed in primary visual cortex for natural movies shown in larger apertures (Vinje and Gallant, 2000).

The smallest aperture size was chosen to cover the “classical” receptive field of the cell (see next section for how we measured receptive fields). Outside of this aperture, receptor units were active at baseline, while inside the aperture, their responses were generated by the GM.

Larger aperture resulted in lower overall firing rates (Fig. 4d, raster plots). Furthermore, responses were more transient and sustained responses less frequent, resulting in increased sparse-ness of the detector's response (Fig. 4e, see Materials and Methods). Finally, since more sensory information was provided to the network with larger apertures, responses were also more selective, as witnessed by the decreased cross-correlations between instantaneous firing rates of nearby detectors (Fig. 4f).

Interestingly, the range of apertures for which selectivity increased largely exceeded the ones covering the central part of the receptive field and extended to the periphery of the predictive field and beyond. Thus, inputs shown in the far surround, which do not directly excite or suppress the response of a detector, can nevertheless affect its selectivity. This result is in agreement with data from the visual cortex, where natural movies shown in apertures four times wider than the RFs greatly enhance the sparseness and decorrelation of responses when compared with smaller apertures limited to the receptive field (Vinje and Gallant, 2000).

Contextual changes in receptive fields

We determined the receptive field shape of detector neurons in the “blob model” with methods commonly applied to map visual receptive fields in physiological experiments. For example, we measured the STA (for review, see Rieke et al., 1997; Chichilnisky, 2001; Carandini et al., 2005) using noisy “checkerboard” stimuli (dense noise, see Materials and Methods) at different contrast levels. This allows us to examine the influence of stimulus strength (e.g., night vs day vision, soft vs loud sounds, weak vs strong tactile stimulations) on receptive field properties.

By construction, the presence of an object always increases firing rate (Eq. 4). The predictive fields and feedforward connections are therefore all excitatory. Nonetheless, the receptive fields mapped with dense noise show center-surround structure with suppressive lobes, as illustrated in Figure 5. This is because activating pixels in the periphery of the predictive field gives advantage to competing detector neurons with overlapping, better matching predictive fields. The net effect of this competition is similar to an “inhibitory surround” (Fig. 5a, left column).

As expected in general from such “center-surround” organization, detector neurons respond most strongly when receptors in the center of their predictive field are surrounded by inactive receptors (Fig. 5b). More generally, input targeted divisive inhibition (Eq. 2) predicts that sensory neurons respond most efficiently to “salient” features that are not predicted by the activation of neighboring units. For the same reason, they also respond strongly to “edges,” i.e., discontinuities in feature space (Fig. 5b). Note, however, that detectors do not represent edges or salience per se—inhibitory surrounds are not part of the object represented by the cell, but a consequence of explaining away. In addition, the size of the “central” receptive field (the positive lobe in the STA) is much smaller than the predictive field (Fig. 5a, left column, dashed line).

Moreover, we find that the predicted spatial receptive fields and their center-surround structure are not invariant properties, but depend on contrast (i.e., the strength of receptor activations) and temporal integration of the stimulus used to measure it. As shown in Figure 5a, the extent of the excitatory RF region decreases and the strength of surround inhibition increases for higher contrast and longer delays between stimulus and response. Such effects were reported for cells in the retina (Solomon et al., 2006), visual cortex (Sceniak et al., 1999; Malone et al., 2007), auditory cortex (Blake and Merzenich, 2002), and somatosensory cortex (Moore et al., 1999). These coarse-to-fine changes in receptive field shapes stem from the lateral competition, which is stronger for larger SNR in the input (such as for higher contrast or after longer integrations). It reflects a trade-off between detection and discrimination of similar objects, and is not observable for networks without divisive inhibition (Fig. 5c). Note that this implies that the same receptor can excite or suppress a given detector in different contexts. It was indeed observed that surround stimuli can either suppress or facilitate visual responses depending on contrast (Mizobe et al., 2001).

For comparison, we also measured the STAs for networks with biased competition (Fig. 5d) and lateral subtractive inhibition (Fig. 5e). A similar center-surround receptive field structure is observed in both cases. However, lateral subtractive inhibition does not significantly affect the shape of the receptive fields as a function of time or contrast. Such plastic changes require input targeted divisive inhibition. In agreement with previous work (Spratling, 2010), BC predicts very similar changes as DI.

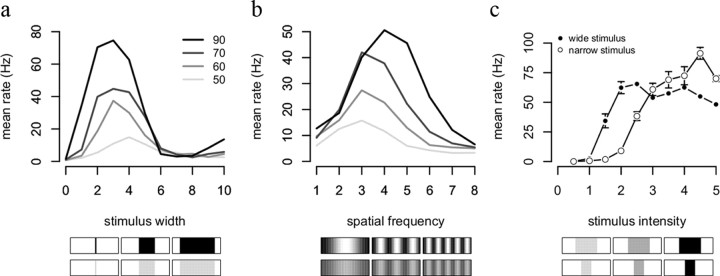
The same phenomena are reproduced by alternative stimulation methods to characterize receptive fields. Figure 6a shows the response of a detector unit to a stimulus expanding from the center of its predictive field. In agreement with empirical data from the retina and primary visual cortex (Sceniak et al., 1999; Solomon et al., 2006), the size of the optimal radius decreases with increasing contrast. Similarly, the optimal spatial frequency increases with increasing contrast (Fig. 6b), as previously reported in the retina (Solomon et al., 2006) and primary visual cortex (Sceniak et al., 2002). Analogous results have been found in the auditory system (Blake and Merzenich, 2002). Finally, contrast response curves depend non-monotonically on stimulus size, with larger stimuli leading to smaller responses at low contrast (Fig. 6c), in agreement with retinal data (Solomon et al., 2006).

Figure 6.

Receptive field properties. a, Single unit response rates to stimuli of different widths centered on the units' predictive field. Gray values code contrast level as indicated in the legend. The peak response is at wider stimuli for low contrast, indicating a larger field of spatial integration. b, Frequency preference depends on stimulus contrast. Instead of blobs with increasing widths, here we used full field stimulation with sinusoidally modulated luminance patterns. c, Contrast response function depends on stimulus width. The network was stimulated by a narrow (3 receptors) and a wide stimulus (9 receptors) of increasing contrasts.

Measuring predictive fields

Our model suggests that sensory neurons can be characterized more appropriately by invariant predictive fields than by context-dependent receptive fields. In contrast to receptive fields, predictive fields cannot be measured by standard linear methods since explaining away masks the true shape of the predictive field. Fortunately, a better picture of the predictive field can be obtained by limiting the amount of competition from nearby detectors. Thus, the receptive field of detector unit j becomes very similar to the predictive field (w̃_ij^t ≈ w_ij) when the probability of all other competing objects is zero, i.e., when p_k^t = 0 for k ≠ j. This suggests the adaptive method illustrated in Figure 7. We first estimate the receptive field shape of a detector unit (i.e., its preferred stimulus) as the spike-triggered average for high contrast checkerboard stimuli. We then measure another spike-triggered average with a stimulus being the superposition of the previously measured preferred stimulus and a new checkerboard stimulus (Fig. 7a; for details, see Materials and Methods, Simulation protocol). The preferred stimulus selectively activates the recorded cell and shunts its competitors. This limits the impact of input targeted divisive inhibition on the response to the superimposed checkerboard stimulus. The estimated predictive field resulting from this method (Fig. 7b, red line) is much closer to the true predictive field (Fig. 7b, dashed line), and the corresponding STA (Fig. 7c) does not show any traces of inhibitory surround.

Reshaping of sensory responses by the surround

Perceptual inference predicts that stimuli activating a detector in the center of its predictive field suppress it when shown in the periphery. However, this inhibition is targeted selectively at individual feedforward weights rather than applied globally to the total input. Thus, the effects of “center” and “surround” are not separable. Stimuli shown in the surround shape how a neuron responds to stimuli in its central receptive field. And vice versa, which stimuli are shown in the center determine the shape of surround modulation. Modulation by the surround is maximal when the surround can explain away the central stimuli, i.e., the center and surround stimuli are similar and could have been caused by the same object.

In contrast, influences from the center and surround were assumed to be separable in previous lateral inhibition models. For example, in divisive inhibition models (Carandini and Heeger, 1994; Schwartz and Simoncelli, 2001), the response to feedforward input is gain modulated by a weighted sum of responses from other neurons. In subtractive inhibition models or predictive coding (Srinivasan et al., 1982), a weighted sum of responses from other units is subtracted from the feedforward input. As a consequence, our model makes distinct predictions from other lateral inhibition models regarding how center-surround interactions depend on the exact stimulation conditions.

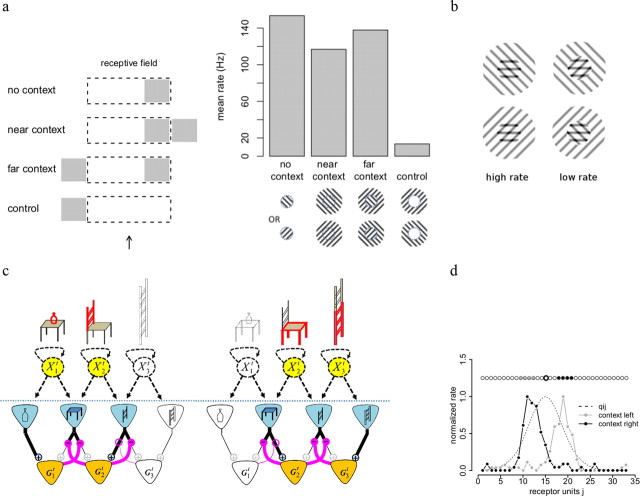
To illustrate the selective effect of surround modulation on responses to central stimuli, we measured the response of a detector unit while stimulating different parts of its receptive field and surround. With our choices of parameters, the central receptive field measured at high contrast contains five contiguous receptors. We defined the “right part” and “left part” of the receptive fields as the two detectors on the right or left of the central receptor. Meanwhile, the “right” or “left” surround corresponded to the two receptors flanking this RF on the right or left. The model prediction and its interpretation in the context of a V1 complex cell are shown in Figure 8a. A detector stimulated at high contrast in the right part of its receptive field is suppressed by stimuli in the right surround (“near” context), but unaffected by stimuli in the left surround (“far” context). Vice versa, the left surround is suppressive when the detector is stimulated in the left part of its receptive field (near context), but the right surround has no effect (far context). This is easy to understand, since stimulating only the left surround activates competing detectors on the left. These competitors predict and suppress inputs from the left part of the predictive field, but do not predict and suppress inputs from the right part of the receptive field. In contrast, separable lateral inhibition models do not distinguish between near and far context.

Figure 8.

Reshaping of receptive fields by spatial context. a, A detector stimulated in the right part of its receptive field (dashed lines, RF center indicated by the black arrow) is suppressed by stimuli in the right surround (gray rectangle), but unaffected by stimuli in the left surround. Left panel shows stimulation protocol and right panel shows mean firing rates during the test stimulus for 250 repeats. b, Targeted divisive inhibition predicts nonseparable interactions between center and surround. The effects of a surround grating on the response to a central plaid yield stronger response to the plaid and the surround than to the plaid alone if the surround is coaligned with the overlaid nonpreferred grating (left column) and weaker if not (right column). c, Illustration of selective divisive inhibition. Depending on which other objects are present in the scene (circular nodes highlighted in yellow), the seat of a chair will be either discounted (left) or useful as a distinctive feature (right). This is implemented by a selective inhibition (magenta connections) of feedforward inputs by detector responses. Active receptor neurons and detector neurons are highlighted in blue and orange, respectively. Thick lines indicate active connections, while thin lines represent connections that are not in use (because presynaptic neuron is inactive) or suppressed by divisive inhibition. d, Application to the blob model. A subset of units (context, gray and black dots) is clamped to indicate high probability of the corresponding objects. Together, these units predict firing rates for all the receptor units. This prediction selectively inhibits the feedforward inputs from receptor units to other detector units. Plain gray and black lines show the resulting (shifted) tuning curves for the unit indicated by the thicker circle. Dashed line indicates the predictive field for this unit.

If we interpret receptors as representing local orientations and neighboring receptors as responding to similar orientations (Fig. 8a, bottom right), this accounts for the fact that V1 complex cells are maximally suppressed when the surround is co-oriented with the central stimulus (Cavanaugh et al., 2002). In contrast, global (not input selective) inhibition would predict maximal suppression when the surround is at the preferred orientation, regardless of the orientation in the center.

The prediction of our model can be tested further by showing composite stimuli in the receptive field center (Fig. 8b). Imagine for example a V1 neuron responding maximally to a horizontal grating in its receptive field. If another superimposed grating is shown in its RF center, i.e., the central stimulus is a plaid, the response is suppressed. Suppression is maximal if the additional grating is orthogonal to the preferred orientation. This effect, called “cross-orientation suppression,” has been widely reported in primary visual cortex (Bonds, 1989). Let us suppose now that a grating is shown in the surround of the receptive field, with orientation either similar to the cross-oriented grating in the center (left column) or orthogonal to it (right column). Input-targeted divisive inhibition predicts that the surround will selectively suppress the effect of central grating components with similar orientation. Therefore, the response of the cell in this example will be facilitated if the surround grating is co-oriented with the nonpreferred component of the plaid (left column). On the other hand, the response of the cell to the central plaid will be suppressed if the surround is not co-oriented with the nonpreferred component in the center (right column) or co-oriented with the horizontal component of the central plaid. This nonseparable effect of center and surround can be explained if the surround differentially modulates different inputs received by the cell.

Our model predicts that the surround not only facilitates or suppresses responses in a context-dependent manner, but also reshapes the selectivity of sensory neurons. We illustrate this effect with a toy example (Fig. 8c). Consider a “chair detector neuron” in two different contexts: in the presence of a table (left panel), or in the presence of a ladder (right panel). Tables and ladders share different sets of features with the chair. In the presence of a table the “chair neuron” should rely on the feature corresponding to the back of the chair, which distinguishes chairs from tables. In the presence of a ladder, the chair neuron should respond to the seat of the chair, which distinguishes chairs from ladders. As a consequence, the chair neuron will appear to be selective to different features in the presence of different objects in the surround, even if its predictive field (i.e., the set of features predicted by a chair) is invariant.

If the receptor layer is interpreted as inputs from contiguous spatial locations, the receptive field will in effect be repelled by competing stimuli. This is illustrated in Figure 8d where we induced competition via clamping of nearby detector units (see Materials and Methods). The clamped units selectively suppress a subset of the inputs, thereby shifting and reshaping the receptive field. Meanwhile, if we interpret the receptors as representing contiguous locations in another feature space, competing stimuli will in fact repel the detector's tuning curves. For example, the peak of the orientation tuning curve of a visual unit preferring vertical orientation will shift toward counter-clockwise orientations if nearby units preferring clockwise orientations are clamped.

This could account for repulsive effects of the surround on orientation tuning in V1 (Sillito et al., 1995), the repulsion of orientation tuning observed in cross-orientation suppression (Kabara and Bonds, 2001), or the switch from “OFF” to “ON” response properties in salamander RGC cells when the polarity of the surround is reversed (Geffen et al., 2007). More generally, the feedforward weights are constantly reshaped by competition with other objects in the scene, and so is the effective receptive field of the sensory neuron.

In contrast, the lateral inhibition model does not predict the surround to cause such repulsion. The receptive fields' shape is identical whether units are clamped on the right or on the left (data not shown).

Selective reshaping could account for repulsive effects of the surround on orientation tuning in V1 (Sillito et al., 1995), the repulsion of orientation tuning observed in cross-orientation suppression (Kabara and Bonds, 2001), or the switch from OFF to ON response properties in salamander RGC cells when the polarity of the surround is reversed (Geffen et al., 2007). More generally, the feedforward weights are constantly reshaped by competition with other objects in the scene (Fig. 8e), and so is the effective receptive field of the sensory neuron.

The degree to which receptive fields are reshaped by the context may vary with the sensory modality. Visual or tactile features are naturally separated in space, and their predictive fields might not overlap sufficiently to completely change the RF shape. Indeed, our toy model uses localized predictive fields with limited overlap. Other sensory modalities may present much stronger degrees of overlap and competition. For example, most naturally occurring sounds will activate largely overlapping populations of cochlear hairs cells, while odors activate largely overlapping sets of olfactory receptors. In such cases, contextual effects might become so strong that the concept of a receptive field loses its meaning; in particular, this may explain in part why auditory receptive fields (STRFs) poorly predict responses to natural sounds (Theunissen et al., 2000; Machens et al., 2004).

Reshaping of sensory responses by adaptation

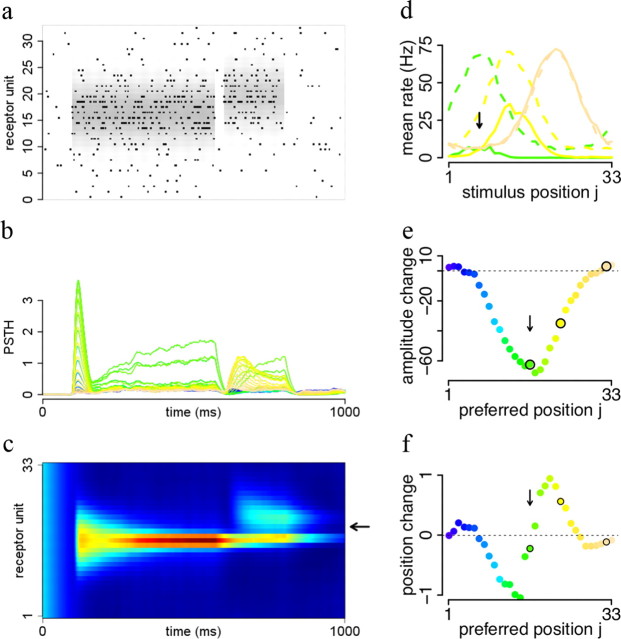
The same line of argument predicts strong effects of adaptation to previously presented stimuli on the responses of sensory neurons (Fig. 9).

Figure 9.

Reshaping of receptive fields by temporal context. a, After an adapting stimulus, a test stimulus at a slightly different position is shortly presented and the number of spikes during test stimulus presentation counted. Black dots indicate spikes for a single run and gray values in the background indicate firing rates of the corresponding receptors. b, Smoothed PSTH for all cells in the network for multiple repetitions of the stimulus in a. Each colored line corresponds to the PSTH of one cell in the network. c, Illustration of the repulsion effect: the adapting stimulus causes the peak network response (intensity values show mean G values) to be shifted away from the test stimulus (black arrow). d, Adaptation changes tuning curves. Colored lines show tuning curves of three different units after exposure to a stimulus indicated by the black arrow. Dashed lines show unadapted tuning curves for comparison. e, Change in peak amplitude depends on distance between adapting and preferred stimulus. f, Preferred position of cells changes depending on distance between adapting and preferred stimulus.

Typical adaptation protocols consist in presenting a stimulus for a long period of time (adaptive stimulus) immediately followed by a brief presentation of another stimulus (test stimulus). We implemented this protocol by presenting two objects in rapid temporal succession to the network (Fig. 9a). Since probabilities are updated by slow integration of the sensory input, the probability of the first object (the adaptive stimulus) is still high in the period immediately following its disappearance. The “phantom object” will still explain away inputs to nearby detectors, resulting in a strong reduction in the gain of the detector responses to the test object presented next (Fig. 9b, the test stimulus).

This gain reduction is maximal when the adaptive and test stimuli are at the same location, and decays as the adaptive and test stimuli are presented further apart (Fig. 9d,e). Adaptation also causes a small repulsion (Fig. 9f) of the response curves away from the adapting stimulus. The “preferred” position (i.e., the position of the test stimulus triggering maximal response) for detector units is repulsed away from the position of the adaptive stimulus. This effect is maximal for detector units with preferred position close to (but not at) the position of the preferred stimulus (Fig. 9f).

As in Figure 8d, this repulsion is not observed in the subtractive lateral inhibition model (data not shown).

Interpreting “receptors” as separate orientation or direction selective channels, this model accounts for suppressive and in some cases repulsive effects of adaptation on orientation (or direction) tuning curves (Carandini et al., 1998; Dragoi et al., 2000; Schwartz et al., 2007; Wiese and Wenderoth, 2007) (for review, see Kohn, 2007), and similar effects are found in the two-tone suppression reported in the auditory system (Brosch and Schreiner, 1997).

The network's output reflects a perceptual interpretation of the sensory scene. We can thus infer the perceived position of the adapted and test stimuli from the posterior probabilities represented by the detectors. The model predicts a repulsive effect of adaptation on the perception of the test stimulus, as illustrated in Figure 9c. When a test stimulus is presented in the vicinity of the adapted location, the corresponding sensory input is interpreted in part as evidence for the continuing presence of the stimulus used for adaption. Consequently, the detector layer temporarily shows two response peaks in the output layer. The first peak is at the position of the adapted stimulus: this object is still a valid interpretation of part of the sensory input. As a consequence, it is interpreted as being continuously present “in the background.” The second peak corresponds to the test stimulus itself. However, its perceived position is repulsed away from its true position (Fig. 9c, marked by an arrow) because part of the sensory input has been explained away by the previous stimulus. If the stimulus used for adaptation is presented on the right of the test stimulus, it explains away the right part of the receptor input. This suppresses the “true” detector and causes a detector further to the left to be activated instead. Vice versa, if the test stimulus is presented on the left of the adapted position, it will cause the activation of detectors further to the right of the true position. This biasing effect occurs only when the predictive fields of the adapted stimulus and the test stimulus overlap, i.e., when they are close to each other. This results in a bias of the perceived test stimulus away from the adapted position, maximally when the test stimulus is close to (but not at) the position of the adaptive stimulus, and vanishing when the test and adaptive stimuli are presented further apart. This repulsion has the same biphasic shape as the repulsion in response curves (Fig. 9f) but with a larger amplitude (peaking at two receptor units of position displacement).

Such repulsion from the adaptation stimulus is a well documented effect of adaptation on perception. Well known examples include the tilt-after effect, where adaptation to a visual grating repulses the perceived orientation of a test stimulus away from the adapted orientation, or the waterfall illusion, where adaptation to a moving stimulus results in a percept of motion in the opposite direction of a subsequent static stimulus (Jin et al., 2005). As observed in our model, this perceptual repulsion is maximal when the orientation (or motion direction) of the test stimulus is similar to the adapted stimulus, and vanishes when the adapted and test stimulus are dissimilar (Schwartz et al., 2007).

The results reported here are not limited to the specific shape we used for the predictive fields and generalize e.g., to oriented 2D predictive fields resembling V1 “simple cell” RF shapes, or predictive fields with random shapes. Using generative models based on these predictive fields reproduces the findings reported above, i.e., we also observe sparsening and coarse-to-fine changes in RF shape as a function of time and contrast, facilitating effects of the surround at low contrast, and repulsive effects at high contrast. Adaptation results in suppression and repulsion of neural responses and the corresponding perception.

Discussion

The characterization of sensory neurons via their RFs provides a first approximation to sensory processing. However, the dependency of RF shape on stimulus properties as well as modulations by the spatial and temporal context clearly show the limits of this approach.

To understand these phenomena, we propose a normative neural model of sensory processing based on the assumption that spiking neurons infer the presence of independent objects in dynamic sensory scenes. Instead of using RFs, this approach characterizes cells via their predictive fields, i.e., the predicted impact of their preferred stimulus on the sensory input. The model demonstrates that input targeted divisive inhibition is crucial to resolve ambiguities between similar objects and implements a trade-off between fine discrimination and integration of sensory evidence.

Sparsening and coarse-to-fine continuum in sensory processing

This trade-off is reflected in coarse-to-fine changes in sensory representation. Short, noisy, and low contrast stimuli can only be detected by integrating over all predictive fields. The corresponding model RF shapes are wide with essentially no inhibitory surrounds. On the other hand, long, reliable, and high contrast stimuli allow for fine discrimination and yield more selective RFs with stronger suppression. This accounts for the sharpening of visual RFs with time and contrast and also results in sparse responses.

Note, however, that this model does not predict other phenomena referred to as “sparsening” or “sharpening,” e.g., whether RFs should become smaller or larger in successive processing stages, or whether fewer or more units should be active in the output than in the input layers. These properties depend on the specifics of the generative model.

Receptive fields are reshaped by the spatial context

RFs are dynamically reshaped to concentrate on relevant input features and do not reflect the represented object or sensory event, but which part of the input space is relevant to recognize this object in its context. Therefore, stimuli situated well outside the classical RF can greatly contribute to a cells selectivity. In contrast, if detectors inhibit other detectors directly rather than targeting their inputs (as in most models of lateral inhibition), this changes global response levels or gains but does not reshape RF shapes (see Figs. 5–9).

Receptive fields are reshaped by the temporal context

Our model predicts suppressive and repulsive effects of adaptation observed in early visual, olfactory, and auditory processing. In line with other accounts (Wark et al., 2009), adaptation is interpreted as a rational consequence of efficient perceptual inference (Wark et al., 2007). In our perspective, suppression in neural responses and repulsion in behavior occur because the adapted stimulus might still be represented in the ongoing activity, explaining away part of the sensory input.

Empirical evidence from single unit recordings (Kohn and Movshon, 2004) suggests that in contrast to V1, mediotemporal area MT shows an attraction of tuning curves toward the adapted direction of motion, which is compatible with a repulsion in the direction represented by a population. While V1 decomposes the scene into elementary dynamical features, MT might construct a population code for “global” motion direction. This is supported by the corresponding neural responses to superpositions of moving gratings: while V1 cells respond to the components of the plaid, many MT cells respond to the perceived global motion (Movshon and Newsome, 1996).

Exploring sensory representations

We purposely used a simplistic model to account for three central aspects of sensory processing: (1) stimuli change over time, (2) sensory input is noisy, (3) sensory input is ambiguous and redundant. The approach allowed us to make generic predictions on contextual modulation of sensory responses. To generate quantitative predictions, the model needs to be adapted to specific sensory modalities and processing stages. For example, predictive fields of odor-detecting cells might correspond to combinations of olfactory receptor activations (Reisert and Matthews, 2001). Although these are clearly not blobs, different odors activate highly overlapping populations of receptors. Our model therefore still predicts sparsening of responses (Perez-Orive et al., 2002), contextual modulation, and adaptation (Stevenson and Wilson, 2007).

Our approach suggests new methods for exploring sensory representations and we argue for the estimation of predictive fields rather than RFs to describe which features drive individual neurons independent of the inhibitory interactions between them. We predict that the responses of sensory neurons reflect the characteristics of their preferred objects (i.e., the predictive field) most accurately when competition is weak. Thus, rather than mapping sensory receptive fields with strong, optimal stimuli resulting in high firing rates and center/surround RFs, the selectivity of sensory neurons might be better explored with brief, low contrast stimuli.

Because weak stimuli might not evoke sufficiently reliable neural responses, we suggested an adaptive method to measure predictive fields from single unit recordings (Fig. 6). Rather than estimating the PF by standard RF mapping in one go, a first estimate of the cell's preferred stimulus is obtained using spike-triggered averaging with dense noise stimuli. In a second step, the predictive field's shape is then reestimated using a superposition of this preferred stimulus and additional noise.

The presence of the preferred stimulus minimizes competition with other sensory objects, and thus the distortion of the PF estimate by inhibitory competition. Meanwhile, the superimposed checkerboard stimulus samples the input space allowing us to characterize the cells selectivity. While one iteration of this process was enough in our simple example, several iterations may be required to estimate more complex PFs.

A way to test the proposed type of inhibition would be to record simultaneously from two neurons with overlapping RFs (e.g., two nearby retinal ganglion cells) while presenting pairs of local stimuli (S1 and S2). S1 would be shown in the RF of neuron 1, but outside the overlap with the RF of neuron 2, thus stimulating neuron 1 but not neuron 2. The critical test would be provided by comparing the response of neuron 2 to the stimulus pair to its response to S2 alone. The response to the stimulus pair should be reduced when S2 is shown in the overlap of the RFs (because in this case, neuron 2 enters in direct competition with neuron 1). In contrast, this response should not be affected when S2 is shown outside of the overlap of the two RFs. This would demonstrate that competition between sensory neurons is input selective and not simply result of lateral inhibition or gain modulation.

Furthermore, simultaneous recordings of multiple spike trains (e.g., from dense multielectrode arrays) offer additional ways to test the DI model. For instance, the predictive power of generalized linear models (GLMs) assuming additive or subtractive lateral connections (Pillow et al., 2008) can be compared to a modified model in which static coupling terms are replaced by Equation 2. Such modeling might also unmask larger input filters, better representing the predictive field and thus the sensory neuron's true selectivity. We also expect this model to better generalize across different stimulus sets such as checkerboard stimuli or natural movies.

Comparison with other approaches

While our model accounts for surround modulations observed in visual cortices, it fundamentally differs from the descriptive models previously proposed to address them. Such models were motivated e.g., by experimentally observed properties of sensory processing like divisive normalization (Heeger, 1992; Carandini and Heeger, 1994) or synaptic depression (Carandini et al., 2002; Goldman et al., 2002). Alternatively, models of thalamocortical and recurrent corticocortical interactions were proposed to account for these effects mechanistically (Stemmler et al., 1995; Teich and Qian, 2003; Priebe and Ferster, 2006; Schwabe et al., 2006). In contrast, our approach is purely “top down,” starting with the premise of optimal spatiotemporal perceptual inference. The agreement in predictions suggests, however, how specific physiological mechanisms (i.e., synaptic depression) can implement the computations underlying sensory inference.

Similar top-down Bayesian approaches have been applied recently to account for other specific aspects of neural processing such as the dynamics of adaptation (Stevenson et al., 2010; Wark et al., 2009) or synaptic short term plasticity (Pfister et al., 2010). The model we propose extends our previous work addressing the single neuron level (Denève, 2008) and demonstrates that the same principle of Bayesian inference has implications both at the single unit level (temporal integration of multiple inputs) and at the network level (competitive interactions).

From a signal processing point of view, our model is closely related to approaches based on independent component analysis or sparse coding (Bell and Sejnowski, 1997; Schwartz and Simoncelli, 2001; Olshausen and Field, 2004). The main differences to this previous work are (1) our assumption that the sensory system is mainly interested in the binary composition of the sensory scene rather than analog coefficients in a mixture, (2) explicit modeling of both spatial and temporal statistics, and (3) the fact that layers in the network do not commit to a single interpretation of a dynamic scene but signal the probabilities of objects being present. Unresolved ambiguities are transmitted to the next layer and might be resolved later in the processing hierarchy.

We are aware that using a minimal binary GM introduces limitations in the capacity of the model to represent continuous variables like the orientation of a bar. Bars that do not match a predictive field (i.e., in between the preferred orientation of two nearby detectors) cannot be represented. Other models have proposed how probability distributions of continuous variables could be represented by a population of spiking neurons. This limitation of our GM could be addressed in part by the use of hybrid models associating binary and continuous variables (Berkes et al., 2009).

Interestingly, our model is very similar to the divisive BC model that has been previously shown to account for effects of attention (Spratling, 2008) and contextual interactions in V1 (Spratling, 2010), as well as being efficient for removing redundancies in natural images (Spratling, 2010). The main difference is that biased competition divides the inputs by their feedback prediction, while our model divides the feedforward weights. The BC model was derived by combining two influential theories of top-down modulations, “predictive coding” and “biased competition” and was partially motivated via its pattern recognition performance. In contrast to our approach, however, this form of competition is not directly derived from principles of efficient sensory processing. To the best of our knowledge, our model is the first to show that input targeted divisive inhibition yields competition among sensory feature detectors that approximates optimal inference. Moreover, our results suggest that a small change to the BC equations (namely excluding the self-prediction from the divisive inhibition received by each unit) would greatly enhance its performance.

Neural representation of probabilities

In our model, many contextual modulations stem from gain modulation of effective feedforward weights by the predictions from other detectors. This corresponds to a generic mechanism for inference, explaining away. Contextual modulations are thus expected regardless of how neurons represent probabilities, or whether neurons represent probability at all. Our model proposes a specific neural implementation for this mechanism, which makes it experimentally testable. Other models have been proposed for neural coding of probability, such as sampling models, probabilistic population codes (Ma et al., 2006) convolutional codes (Zemel et al., 1998) or direct representations of probabilities in firing rates (Rao, 2004). Note, however, that most of these previous models did not deal with temporal inference. When they did, they were not self-consistent (i.e., the outputs could not be used as inputs by the next processing stage).

Anatomical implementations of input targeted divisive inhibition

A naive implementation of the model requires selective shunting of each synapse by lateral connections. Direct gain modulation of synaptic transmissions could occur when output cells sum from a limited number of receptors, such as in sensory epitheliums or their first relays. For example, horizontal cells in the retina can selectively modulate the gain of the receptor-to-bipolar cell synapse (VanLeeuwen et al., 2009). Likewise, lateral connections in the drosophila antennal lobe can perform presynaptic divisive inhibition of inputs from olfactory receptors (Olsen and Wilson, 2008). However, such direct synapse-targeted inhibition is unlikely to be implemented in the cortex. More plausibly, input-targeted divisive inhibition could be mediated by synapses on the proximal dendrite. These synapses would locally increase conductivity, and thus shunt the synaptic input from a whole dendritic branch. Alternatively, the network could rely on “lateral cells” to transfer information from the peripheral part of the predictive field. Lateral cells could be suppressed by detectors and compute the time varying gain modulated inputs w̃_ij^ts_i. For example, lateral connections in V1 result in a larger spread of stimulus-evoked activity at low contrast (Nauhaus et al., 2009).

Our model concentrated on a single layer in the perceptual hierarchy and on bottom-up processing, i.e., transfer of information from sensory inputs to high level representations. A full Bayesian model requires feedback connections transferring information from high level representations to low-level sensory features. For example, contour integration in V1 may correspond to such top-down processes where a detected contour facilitates the responses to its local elements. This could be implemented by feed-back connections from V2 and/or intracortical excitatory connections widely observed within V1. Such longer range top-down influences will modulate effects of explaining away and adapt to task demands, prior expectations, and utilities. Although we focused on the bottom-up component of optimal sensory processing, the Bayesian inference framework provides a sound basis to integrate the extracted evidence with such information from higher processing stages.