A Stochastic Signaling Network Mediates the Probabilistic Induction of Cerebellar Long-Term Depression

Abstract

Many cellular processes involve a small number of molecules and undergo stochastic fluctuations in their levels of activity. Cerebellar long-term depression (LTD) is a form of synaptic plasticity expressed as a reduction in the number of synaptic AMPA receptors (AMPARs) in Purkinje cells. We developed a stochastic model of the LTD signaling network, including a PKC-ERK-cPLA₂ positive feedback loop and mechanisms of AMPAR trafficking, and tuned the model to replicate calcium uncaging experiments. The signaling network activity in single synapses switches between two discrete stable states (LTD and non-LTD) in a probabilistic manner. The stochasticity of the signaling network causes threshold dithering and allows at the macroscopic level for many different and stable mean magnitudes of depression. The probability of LTD occurrence in a single spine is only modulated by the concentration and duration of the signal used to trigger it, and inputs with the same magnitude can give rise to two different responses; there is no threshold for the input signal. The stochasticity is intrinsic to the signaling network and not mostly dependent on noise in the calcium input signal, as has been suggested previously. The activities of the ultrasensitive ERK and of cPLA₂ undergo strong stochastic fluctuations. Conversely, PKC, which acts as a noise filter, is more constantly activated. Systematic variation of the biochemical population size demonstrates that threshold dithering and the absence of spontaneous LTD depend critically on the number of molecules in a spine, indicating constraints on spine size in Purkinje cells.

Introduction

Many experimental and theoretical studies have shown that noise plays a central role in important cellular processes (Arkin et al., 1998; Elowitz et al., 2002). Biochemical processes in small systems undergo extensive and inevitable stochastic fluctuations of their levels of activity, which can lead to substantial different behavior in identical systems (Simpson et al., 2009; Eldar and Elowitz, 2010). In many signaling networks, noise may be detrimental and is minimized through structural changes (Becskei and Serrano, 2000). Yet, in other systems, noise provides functional advantages (Rao et al., 2002; Simpson et al., 2009; Eldar and Elowitz, 2010). However, little attention has been given to the role of noise in the signaling networks mediating long-term forms of synaptic plasticity.

Induction of synaptic plasticity at excitatory synapses is controlled locally by signaling networks within dendritic spines (Kennedy et al., 2005; Sheng and Hoogenraad, 2007). Usually, these signaling networks consist of few copies of several distinct proteins (Peng et al., 2004; Cheng et al., 2006; Sheng and Hoogenraad, 2007) that are likely to undergo stochastic fluctuations in their levels of activity. Here, we investigate the role of stochastic fluctuations in cerebellar long-term depression (LTD).

Cerebellar LTD is a robust and persistent decrease in the synaptic transmission between parallel fibers (PFs) and Purkinje cells (PCs), expressed as a reduction in the number of synaptic AMPA receptors (AMPARs) (Matsuda et al., 2000; Linden, 2001; Steinberg et al., 2004). It is induced experimentally by protocols that promote transitory rises in the postsynaptic intracellular calcium ions concentration ([Ca²⁺]) (Konnerth et al., 1992). Consequently, LTD can be induced directly through uncaging of [Ca²⁺] (Tanaka et al., 2007), which promotes the activation of the cytosolic phospholipase A₂ (cPLA₂) (Mashimo et al., 2008; Burke and Dennis, 2009) and of the Ca²⁺-dependent protein kinase Cα (PKC) (Newton, 2001). PKC regulates the trafficking of AMPARs, leading to the synaptic depression (Matsuda et al., 1999, 2000; Chung et al., 2003). Additionally, PKC activates the mitogen-activated protein kinase (MAPK) pathway (Bhalla and Iyengar, 1999; Kuroda et al., 2001; Tanaka et al., 2007; Tanaka and Augustine, 2008). The MAPK extracellular signal-regulated kinase (ERK) then activates cPLA₂ (Bhalla and Iyengar, 1999; Kuroda et al., 2001; Tanaka and Augustine, 2008), which produces arachidonic acid (AA), a PKC activator (O'Flaherty et al., 2001). After a brief elevation of [Ca²⁺], the feedback loop formed by PKC-ERK-cPLA₂ self-perpetuates its activation and promotes LTD (Fig. 1A; see Materials and Methods for a more detailed description) (Kuroda et al., 2001; Tanaka and Augustine, 2008). However, although extensive progress has been made in experimental characterization of the signaling network involved in LTD (Ito, 2002; Tanaka and Augustine, 2008), the network dynamics remain poorly understood. To investigate its dynamics we built the first detailed stochastic model of cerebellar LTD, which was extensively validated using quantitative and qualitative data obtained from the literature (Momiyama et al., 2003; Masugi-Tokita et al., 2007; Tanaka et al., 2007; Tanaka and Augustine, 2008).

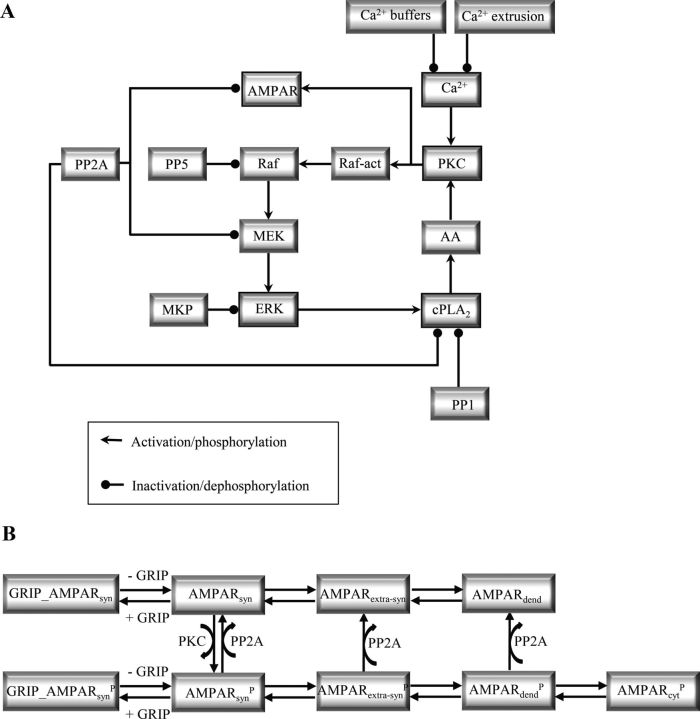
Figure 1.

Diagram of the signaling network involved in Ca²⁺-induced LTD and mechanisms of AMPAR trafficking. A, Transient elevations of [Ca²⁺] activate the positive feedback loop formed by PKC, ERK pathway, and cPLA₂. PKC is responsible for the phosphorylation of AMPARs leading to the synaptic depression. PP2A counteracts this process by dephosphorylating the AMPARs. PKC also activates the ERK pathway that then activates cPLA₂ that produces the PKC activator AA. B, Mechanisms of AMPAR trafficking simulated. The terms AMPAR_syn, AMPAR_extra-syn, AMPAR_dend, AMPAR_cyt refer, respectively, to synaptic, extra-synaptic in the spine, dendritic and cytosolic AMPAR, and ^P refers to the phosphorylated forms of AMPAR in different locations.

Materials and Methods

We developed a detailed kinetic model of the signaling and trafficking network involved in the induction of cerebellar LTD based on extensive experimental data. Cerebellar long-term potentiation (LTP) was not considered. The model was solved stochastically and deterministically using STEPS (http://steps.sourceforge.net/), a well validated simulator (Hepburn et al., 2012) that implements the Stochastic Simulation Algorithm (SSA) (Gillespie, 1977). The model script and a table listing all reactions and all model parameters with full reference to the relevant data are available at ModelDB (http://senselab.med.yale.edu/ModelDB/ShowModel.asp?model=141270). The model contains three components described separately: the Ca²⁺ dynamics, the signaling network (Fig. 1A), and the AMPAR trafficking mechanism (Fig. 1B).

Ca²⁺ dynamics.

Based on Ca²⁺ uncaging experimental results (Tanaka et al., 2007), in most simulations elevations in the level of [Ca²⁺] were used to trigger LTD. Consequently, the mechanisms of Ca²⁺ dynamics are a crucial property of the model: they are responsible for the maintenance of [Ca²⁺] during resting conditions and for restoring it to the basal level following an elevation. The Ca²⁺ mechanisms simulated included extrusion, leak, and buffering.

Ca²⁺ extrusion was implemented according to a previous model (Doi et al., 2005). It contains the plasma membrane Ca²⁺-ATPase (PMCA) and sodium (Na⁺)/Ca²⁺ exchanger (NCX) located in the cytoplasmic membrane and SER Ca²⁺-ATPase (SERCA) placed in the membrane of smooth endoplasmic reticulum (SER). The reaction mechanisms and parameters used to simulate each species were taken from the literature (Doi et al., 2005). However, differently from the original model, third-order reactions used to simulate the interaction between Ca²⁺ and SERCA and between Ca²⁺ and NCX were simulated as sequential second-order reactions. To keep a steady-state [Ca²⁺] in absence of Ca²⁺ inputs, a constant leak (zero-order reaction) was defined opposing the action of the Ca²⁺ extrusion mechanisms.

Two types of Ca²⁺-buffers were incorporated in the model: calbindin (CB) and parvalbumin (PV), binding four and two ions, respectively. The kinetics describing the interaction between each buffer and Ca²⁺ and the parameters for all reactions were taken from the literature (Schmidt et al., 2003).

Signaling network model.

Increasing [Ca²⁺] in the model leads to the activation of the positive feedback loop composed by PKC-ERK-cPLA₂ fundamental for LTD occurrence (Kuroda et al., 2001; Tanaka et al., 2007; Tanaka and Augustine, 2008). This feedback loop was initially proposed in a model of hippocampal long-term potentiation (Bhalla and Iyengar, 1999), which was later adapted to simulate cerebellar LTD (Kuroda et al., 2001). However, the implementation of the feedback loop described in this paper was updated and altered extensively compared with the previous models, based on recent experimental data. Thus, in addition to the inclusion of mechanisms of Ca²⁺ dynamics and AMPARs trafficking, the model described in this study was built using parameters that are different from previous models (Bhalla and Iyengar, 1999; Kuroda et al., 2001; Tanaka et al., 2007) for most of its reactions (the list containing the references for each parameter used can be obtained at http://senselab.med.yale.edu/ModelDB/ShowModel.asp?model=141270). Most importantly, the stoichiometry for the reaction between Ca²⁺ and PKC and Ca²⁺and cPLA₂ were altered, and the reaction mechanisms for the activation of PKC, cPLA₂, and ERK pathway were extensively refined.

The parameters of the model were taken from experimental literature when possible, however, not all parameters are known. To simulate reactions with unknown parameters, the rate constants used in the simulations were approximated from experiments performed with peptides or molecules sharing sequences similar to those involved in the reactions simulated. In those cases, a range of possible parameters was taken from the literature, and a specific value was tuned to fit two constraints. The model had to reproduce the experimentally observed relation between different Ca²⁺ pulse maximum concentrations and durations and the mean magnitude of LTD (Tanaka et al., 2007), and the fact that, during rest, PCs exhibit no spontaneous macroscopic LTD (Launey et al., 2004). The final value used for these parameters was further evaluated with a sensitivity analysis (http://senselab.med.yale.edu/ModelDB/ShowModel.asp?model=141270). This demonstrated that change of up to ±10% of the parameter value did not alter the typical relationship between the depression and the magnitude of the input signal described by Equation 1, but affected at least one of its three parameters by <20%.

Components of the feedback loop.

The first molecule implemented in the model was PKC. It comprises a family of 11 serine/threonine isoenzymes divided into three subfamilies (conventional, novel, and atypical) based on their domain composition, which dictates the cofactor dependence of each class (Newton, 2001). Experimental evidences have implicated one PKC isoform in the occurrence of LTD: PKCα, referred in the rest of the text as PKC, a member of the subfamily of conventional PKCs (Leitges et al., 2004). Structurally, PKC is a multidomain protein composed of a Ca²⁺-dependent lipid-binding domain C2, a lipid-binding domain C1, and a kinase core C terminal (Newton, 2001; Corbalán-García and Gómez-Fernández, 2006). This multidomain composition determines the stimulation of PKC activity by several cofactors including Ca²⁺, AA, and the phospholipid phosphatidylserine (PS) (Corbalán-García and Gómez-Fernández, 2006; López-Nicolás et al., 2006). In the model, two cofactors of PKC were simulated explicitly: Ca²⁺ and AA. To become fully activated, following its interaction with Ca²⁺ or AA, PKC must interact with membrane phospholipids, especially PS. This interaction was simulated as a pseudo-first order reaction, implicitly simulating the amount of PS in the membrane. Therefore, it was assumed that the PKC structure allows its cofactors to act synergistically leading to PKC interaction with the membrane, where it switches conformation and becomes fully activated (Newton, 2001). The synergism among PKC cofactors is not caused by allosteric interaction between these domains, but by an increase in its affinity for anionic lipids in the membranes (Newton, 2001). Thus, the model of PKC assumed that the binding of three Ca²⁺ (Torrecillas et al., 2004) to its structure promotes its binding to PS-containing membranes, causing the full activation of the enzyme (Medkova and Cho, 1999; Bittova et al., 2001). Additionally, high concentrations of AA can lead to PKC translocation and activation in the model, according to experimental data, or low concentrations of AA can act synergistically with Ca²⁺ to promote PKC translocation and activation (O'Flaherty et al., 2001; López-Nicolás et al., 2006).

PKC is responsible for the activation of the MAPK pathway (Tanaka and Augustine, 2008). Mammalian MAPK comprises a family of serine/threonine kinases subdivided in three distinct subgroups that coordinate diverse cellular processes: ERKs, Jun N-terminal kinases, and p38 kinases (Pearson et al., 2001). ERK is the only subgroup of MAPK that has been implicated with the occurrence of cerebellar LTD (Ito-Ishida et al., 2006). Similarly to other members of the MAPK family, ERK activation requires the sequential activation of at least two upstream kinases, an MAPKK and an MAPKKK (Pearson et al., 2001).

The kinase immediately upstream to ERK is a member of the MAP/ERK kinase (MEK) family. The components of MEK family are dual-specificity enzymes that phosphorylate hydroxyl side chains of serine/threonine and tyrosine residues of the MAPKs, simulated as a two-step bimolecular collision (Burack and Sturgill, 1997). A dual-specificity phosphatase termed MAPK phosphatase (MKP) dephosphorylates the tyrosine and threonine residues of ERK promoting its inactivation (Farooq and Zhou, 2004), which was simulated as a distributive catalysis.

The MAPKK MEK is activated by dual phosphorylation, simulated as distributive catalysis, catalyzed by the MEK kinase (MAPKKK) Raf (Kyriakis and Avruch, 2001; Pearson et al., 2001). PP2A reverts Raf action by dephosphorylating and inactivating MEK (Sontag et al., 1993; Silverstein et al., 2002), a process that was simulated as distributive catalysis.

Mammalian MEK kinases have an extremely complex regulation that remains largely unknown. Raf is regulated mainly by small GTP-binding proteins and by phosphorylation (Avruch et al., 2001; Kyriakis, 2007). In addition, Raf can be regulated by several different adapter and scaffolding proteins (Kyriakis, 2007). Phosphorylations of two sites of Raf, serine 338 and tyrosine 341, have been implicated with its activation and interaction with MEK (Diaz et al., 1997; Zang et al., 2008), but the enzymes that phosphorylate these two sites remain unknown (Chaudhary et al., 2000; Dhillon et al., 2007; Zang et al., 2008). PKC phosphorylates Raf (Kolch et al., 1993) and is implicated with ERK activation (Adams and Sweatt, 2002), and, therefore, direct activation of Raf catalyzed by PKC was used in previous models (Bhalla and Iyengar, 1999; Kuroda et al., 2001; Tanaka et al., 2007). However, phosphorylation of Raf by PKC does not lead to its activation (Schönwasser et al., 1998; Yip-Schneider et al., 2000), which indicates that PKC acts on the MAPK pathway through different mechanisms that are poorly understood in PCs. According to experimental data, PKC may lead to the activation of MAPK pathway through direct phosphorylation of the small GTPase Ras (Villalonga et al., 2002; Bivona et al., 2006), or through the phosphorylation of the complex Src/Proline-Rich Tyrosine Kinase 2 (PYK2), which leads to Ras activation (Lev et al., 1995; Litvak et al., 2000). Sequentially to these possible reactions, there is the recruitment and phosphorylation of Raf (Avruch et al., 2001; Kyriakis, 2007). Thus, to simulate the process of Raf activation in the absence of conclusive data, it was described by PKC acting on a Raf-activator (Raf-act) that phosphorylates and activates Raf, leading to the sequential activation of MEK and ERK. The parameters selected to simulate the reactions of PKC action on Raf-act and Raf-act on Raf were based on the typical time window of Ras activation, followed by reactions of phosphorylation. In the model, Raf is dephosphorylated by protein phosphatase 5 (PP5), according to experimental data (von Kriegsheim et al., 2006; Dhillon et al., 2007). Raf activity can be regulated by other phosphatases including PP2A and protein phosphatase 1 (PP1). Both PP2A and PP1 act on Raf as positive regulators, dephosphorylating sites involved in Raf inhibition mediated by 14-3-3 proteins (Jaumot and Hancock, 2001; Adams et al., 2005; Dhillon et al., 2007). As the model did not include 14-3-3 proteins negatively interacting with Raf, the activating role of PP2A and PP1 on Raf was not simulated. A limitation of previous models was to simulate PP2A as a negative regulator of Raf (Bhalla and Iyengar, 1999; Kuroda et al., 2001; Tanaka et al., 2007), which has no support in the literature (Jaumot and Hancock, 2001; Adams et al., 2005; Dhillon et al., 2007).

The activation of the MAPK pathway leads to the subsequent activation of cPLA₂ (Tanaka and Augustine, 2008). PCs express several subtypes of phospholipase A₂ (Shirai and Ito, 2004), but only one subtype, group IV cytosolic phospholipase A₂α (GIVA cPLA₂α, termed cPLA₂ in the remaining of the text), has been implicated with cerebellar LTD (Mashimo et al., 2008). cPLA₂ catalyzes the sn-2-position of membrane phospholipids, releasing AA in the intracellular medium (Piomelli et al., 1987, 2007). As mentioned previously, AA is a PKC activator (O'Flaherty et al., 2001; López-Nicolás et al., 2006), and its production leads to the persistent activation of the PKC-ERK-cPLA₂ feedback loop during LTD occurrence (Tanaka and Augustine, 2008).

Structurally, cPLA₂ is composed of a Ca²⁺-dependent lipid-binding C2 domain, and a C-terminal catalytic domain, and is activated by several different mechanisms (Burke and Dennis, 2009). The most studied form of cPLA₂ activation involves its Ca²⁺-dependent recruitment to anionic membranes (Channon and Leslie, 1990; Nalefski and Falke, 1996). Two Ca²⁺ bind to the C2 domain of cPLA₂ sequentially and with positive cooperativity, promoting its translocation to membranes (Nalefski et al., 1997; Nalefski et al., 2001). Additionally, cPLA₂ activity is regulated by phosphorylation catalyzed by ERK (Das et al., 2003; Tucker et al., 2009) and by anionic phospholipids (Burke and Dennis, 2009). Thus, in the model, following the binding of Ca²⁺ or the phosphorylation by ERK, cPLA₂ translocates to the membrane where its substrates are located. The phosphatases PP2A and PP1 dephosphorylate cPLA₂ causing its inactivation (Gordon et al., 1996; Moscardó et al., 2006). We also included a Ca²⁺- and phosphorylation-independent membrane interaction with low affinity, as has been demonstrated experimentally (Hixon et al., 1998).

To access its substrates, cPLA₂ exhibits a type of interfacial catalysis called scooting mode that involves a tight binding of the enzyme to anionic phospholipids allowing it to hydrolyze many phospholipids before leaving the membrane surface (Bayburt and Gelb, 1997; Berg et al., 2001), which was implemented in our model, but not considered in previous models of LTD (Kuroda et al., 2001; Tanaka et al., 2007).

AMPA receptors trafficking.

In PCs, LTD is expressed postsynaptically as an attenuation of the current mediated by AMPAR channels, caused by a decrease in the number of synaptic AMPARs (Linden, 2001). Therefore, the synaptic depression was simulated as a reduction in the number of synaptic AMPARs, implemented according to the mechanisms of AMPAR trafficking (Fig. 1B). This is a major improvement of our model compared with previous models of LTD that used the concentration of phosphorylated AMPARs as a measurement of depression (Kuroda et al., 2001; Tanaka et al., 2007). The trafficking was simulated taking into account that AMPARs exhibit continuous movements that happen in two reversible steps. One step is the lateral diffusion of the receptors from the synaptic membrane to extrasynaptic areas and vice-versa (Borgdorff and Choquet, 2002; Ashby et al., 2004; Makino and Malinow, 2009). The other step is the endocytosis/exocytosis of the phosphorylated extrasynaptically located receptors (Wang and Linden, 2000; Passafaro et al., 2001; Steinberg et al., 2004). Thus, AMPARs were assumed to exist in four different cellular locations: in the postsynaptic membrane, in the extrasynaptic membrane of the spine, in the dendritic membrane, and in the cytosol. The transition of receptors from one location to another was simulated as a first order reaction. The first-order rate constant for transition of AMPARs from one location to another was calculated by dividing their diffusion coefficients by the area of the compartment considered (Borgdorff and Choquet, 2002; Earnshaw and Bressloff, 2006; Bats et al., 2007). The rate constants for exocytosis/endocytosis were calculated based on the experimentally observed time constant (Ehlers, 2000; Passafaro et al., 2001). Both endocytosis and exocytosis were considered to take place exclusively in the dendritic membrane, following experimental data (Adesnik et al., 2005; Makino and Malinow, 2009).

Not all AMPARs participate in the constitutive trafficking. A fraction of the receptors interacts with anchoring proteins located in the postsynaptic density, and, consequently, shows restricted movements (Bats et al., 2007). Therefore, two distinct populations of synaptic AMPAR were included in the model, one that is mobile and undergoes lateral diffusion in both phosphorylated and non-phosphorylated states and undergoes endocytosis/exocytosis only in its phosphorylated state, and another that is immobile because of interactions with a specific PDZ-containing protein termed glutamate receptor interacting protein (GRIP) (Dong et al., 1997; Burette et al., 1999).

During LTD, PKC phosphorylates the GluR2 subunit of AMPARs promoting a decrease in their affinity for GRIP (Matsuda et al., 1999, 2000; Chung et al., 2003). As a result, some of the phosphorylated receptors stop interacting with GRIP and leave the postsynaptic membrane through lateral diffusion and endocytosis (Matsuda et al., 2000; Wang and Linden, 2000; Steinberg et al., 2004). PP2A reverts PKC activity in the model dephosphorylating AMPAR (Launey et al., 2004). Combining the activity of the signaling network (Fig. 1A) and the mechanisms of AMPAR trafficking (Fig. 1B), we were able to accurately simulate the early phase of cerebellar LTD.

Inputs of the model.

Cerebellar LTD is induced experimentally by simultaneous and repeated activation of the PFs and the climbing fibers (Ito, 2002), which causes a large and transitory elevation of [Ca²⁺] (Konnerth et al., 1992). Consequently, LTD can be induced through elevations in [Ca²⁺] directly, using photolysis of Ca²⁺-caged compounds (Tanaka et al., 2007). Elevations of [Ca²⁺] used to induce LTD were modeled through Gaussian functions simulating the influx of pulses of Ca²⁺ in the cytosol with different duration and concentrations. More than 60 different Ca²⁺ inputs were used in this work, with durations varying from 1 to 60 s and concentrations ranging from 0.5 to 5.0 μmol.L⁻¹. However, in each simulation, a single pulse was used to induce LTD. The input was always given at simulated time 10 min.

Pulses of components of the feedback loop in their activated state were also used to induce LTD (see Fig. 4E). Similarly to Ca²⁺ pulses, these pulses were modeled using Gaussian functions with different durations varying from 10 to 120 s of duration, and with peak value varying from 1 to 100% of activation. The decays of pulses of active forms of the components of the feedback loop tested (ERK, MEK, PKC, and cPLA₂) were mediated by their specific mechanisms of inactivation.

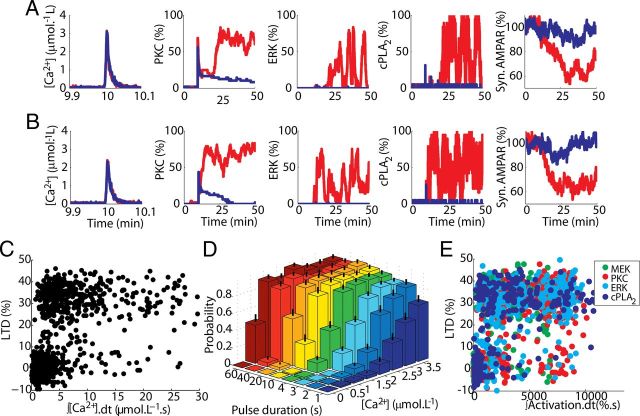
Figure 4.

Probabilistic induction of LTD implies the absence of clear thresholds. A, B, Comparison between activation of network components and LTD induction between two different pairs of single runs of the model stimulated by Ca²⁺ pulses with same peak concentration (high in A and low in B) and duration. These runs were selected to have similar noisy fluctuations of the Ca²⁺ pulse but opposite responses of the model: successful LTD induction (red) or failure (blue). C, There is no threshold for the Ca²⁺ pulse: single runs of the model demonstrate a large overlap of opposite responses (LTD and non-LTD) triggered by similar Ca²⁺ input signals integrated over time (pulses of 1–60 s, and 0.5–3.5 μmol.L⁻¹). D, The probability of LTD induction (computed from 156 simulations, mean and SD shown) is regulated by the duration and concentration of the input signal. E, LTD can also be induced by a pulse of activated component of the feedback loop (Tanaka and Augustine, 2008). Similarly to the results obtained for Ca²⁺-induced LTD, single run results of LTD induced by pulses of different activated components of the feedback loop (PKC, ERK, cPLA₂, and MEK indicated by colors) show a large overlap of opposite responses caused by a wide range of inputs signals (pulses varying from 10 to 120 s of duration, and peak value varying from 1 to 100% of activation) integrated over time. This indicates that threshold dithering is spread throughout the signaling network.

Biochemical population sizes.

Changes in the biochemical population size (BPS) were performed through the alteration of the biochemical compartment where the reactions take place (Bhalla, 2004a,b). The surface was scaled proportionally considering a spherical shape for the biochemical compartment. Varying the volume of the biochemical compartment alters linearly the number of cytoplasmic molecules without changing their concentrations. To keep the ratio among different species balanced, membrane species were scaled proportionally to the change in numbers of cytoplasmic molecules.

Additional methods.

The total time window (50 min) used for preparing the figures and analyzing the date was based on the consideration that the positive feedback loop formed by PKC-ERK-cPLA₂ is essential for LTD occurrence only during the initial 20–30 min after an input signal has been applied (Tanaka and Augustine, 2008). In all simulations, an initial interval of 10 min was included to allow the signaling network to reach steady state. This initial 10 min interval was removed for analysis, and all figures and analyses have time 0 set at the end of this interval.

LTD magnitude was measured 30 min after input. The sigmoid curves described by Equation 1 (Fig. 2B; see Fig. 9B), as follows:

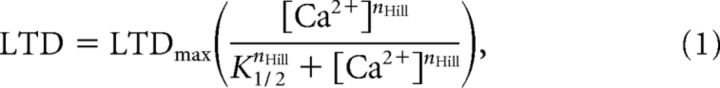were obtained by nonlinear least square regression using cftool, which is an open curve fitting tool of Matlab (MathWorks). The parameters of the curves [Hill coefficient (n_Hill), the [Ca²⁺] required to achieve the half-maximum magnitude of LTD (K_1/2), and maximum depression (LTD_max)] were estimated with 95% confidence intervals in all figures.

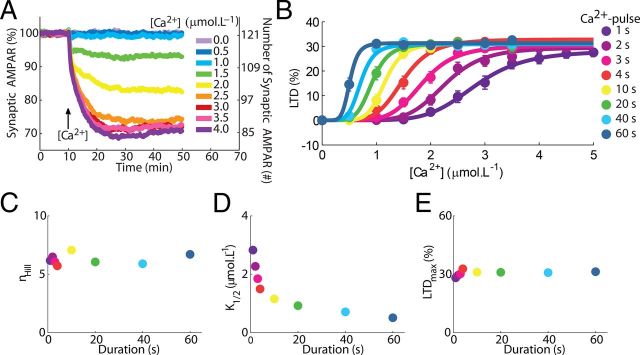
Figure 2.

Mean responses of the model and sigmoidal relationships between LTD and the peak concentration of the Ca²⁺ pulses used to trigger it. A, Time course of the depression induced by Ca²⁺ pulses with different concentrations. Each curve shows the mean time course obtained for 156 runs of the model (Ca²⁺ pulses of 3 s of duration, legend at right indicate the maximum concentration of the pulses). The magnitude of the depression observed, measured as percentage of synaptic AMPARs removed from the synaptic membrane, matches experimentally observed values (Tanaka et al., 2007), and, at rest, the model reproduces the number of AMPARs in accordance with values observed in a single synapse in PCs (Momiyama et al., 2003; Masugi-Tokita et al., 2007). Additionally, the reduction in the number of synaptic AMPARs has a time course in accordance with experimental data, reaching stable state ∼20 min after LTD induction (Tanaka and Augustine, 2008). B, The [Ca²⁺] requirement observed for LTD induction is regulated by the duration of the Ca²⁺ pulses. Each dot (legend on right side applies to B–E) represents the mean result of 156 simulations measured 30 min after the input, and the error bars indicate SEM. The sigmoid curves were obtained by nonlinear least square regression to Equation 1. C, The duration of the Ca²⁺ pulses has no effect on the n_Hill observed during LTD. D, The Ca²⁺ requirement (K_1/2) during LTD induction depends on the pulse duration. E, The maximum depression (LTD_max) is independent of pulse durations.

Figure 9.

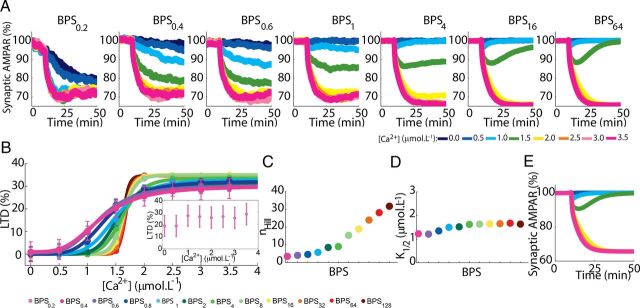
Dependence of the macroscopic LTD responses on BPS. A, Macroscopic curves of LTD (means of 156 runs, Ca²⁺ pulses of 4 s applied at 10 min) showing the reduction in the variability and stability of responses when BPS is altered. Lowering BPS leads to a monostable system with spontaneous LTD while increasing it leads to a bistable system, similar to deterministic versions of the model (E). Stable intermediary mean levels of LTD, similar to those observed experimentally, are present only between BPS_0.6 to BPS₄. B, Sigmoidal relationship between the macroscopic LTD and peak [Ca²⁺] (pulses of 4 s) obtained using different BPSs. Data from 156 runs are plotted as mean ± SEM. Inset shows the responses of BPS_0.2 that could not be fitted with a sigmoid. C, D, n_Hill and K_1/2 for different BPSs. E, The same model was solved deterministically (using the Runge–Kutta method). In the absence of stochasticity the model shows a bistable behavior (see A for legend).

In some figures, triggering inputs of Ca²⁺ (see Figs. 4C, 8A) are integrated over time. Integration was performed to reduce the small variations in the input signals caused by the stochasticity of the model and to allow the identification of a threshold for LTD induction, if present. This integration was performed from the beginning to the end of the pulse considered, and data were sampled at 0.05 s.

Figure 8.

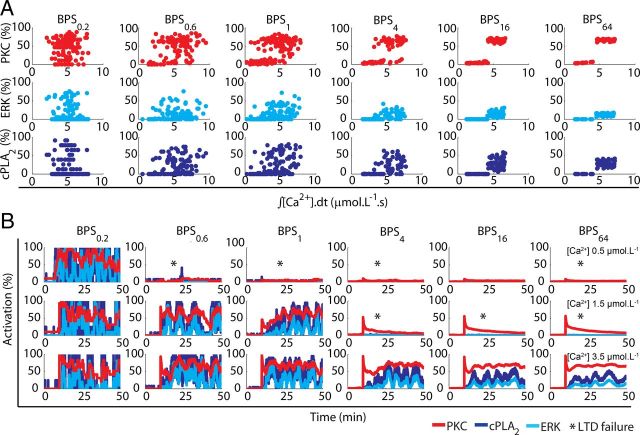
The role of stochastic fluctuations investigated through alterations in the BPS. A, The percentage activation of the three network components investigated is plotted against Ca²⁺ input signal integrated over time for different BPS. For the standard model (BPS₁), no thresholds are visible to Ca²⁺ pulses of 4 s and 0.5–3.5 μmol.L⁻¹. Enlarging the BPS of the standard model (BPS₁) from 4 (BPS₄) to 64 times (BPS₆₄) decreases the overlap of responses and a fixed threshold emerges gradually. Reducing BPS₁ to 60% (BPS_0.6) and 20% (BPS_0.2) has the opposite effect. B, Altering the BPS changes the magnitude and frequency of stochastic fluctuations during single runs of the model, modifying the probability of activation of the network for different inputs [Ca²⁺ pulses of 4 s and 0.5 (top), 1.5 (middle) and 3.5 μmol.L⁻¹ (bottom)]. For small BPS, LTD induction is always successful, while for large BPS the number of failures (shown by asterisks) at low Ca²⁺ pulses increases and the intensity of stochastic fluctuations during successful induction decreases.

The coefficient of variation (CV) (see Fig. 5) was calculated by dividing the SD by the mean of 156 simulations, taken over consecutive intervals of 30 s.

Figure 5.

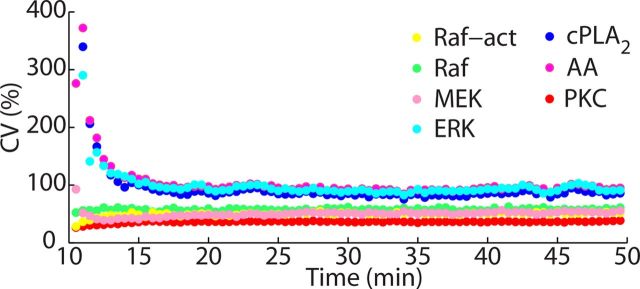
Propagation of noise within the network over time. The CV, a common measure of noise, of different components of the network shows that the level of stochasticity of the network has limited propagation. ERK greatly increases the stochasticity of the network, and, in consequence, acts as important locus of variability in the model. Molecules downstream from ERK, cPLA₂, and AA act in a similar way. In contrast, PKC is a locus of filtering, decreasing the stochasticity of the network.

In Figure 6, the sustained activity of the network is analyzed in single runs over time windows of 10–50 min of simulated time. Power spectral analysis with Fast Fourier transform (FFT) was performed using the function fft of Matlab (MathWorks). Linear correlations (see Fig. 6B) between the powers of the analyzed frequencies (1–30 cycles/h) of stochastic fluctuations of different components were calculated using the function corrcoef of Matlab (MathWorks). Other ranges of frequencies were considered in preliminary analyses, but they were not used because the powers obtained are very low. The values of Pearson correlation coefficient (r) were estimated with 95% confidence intervals.

Figure 6.

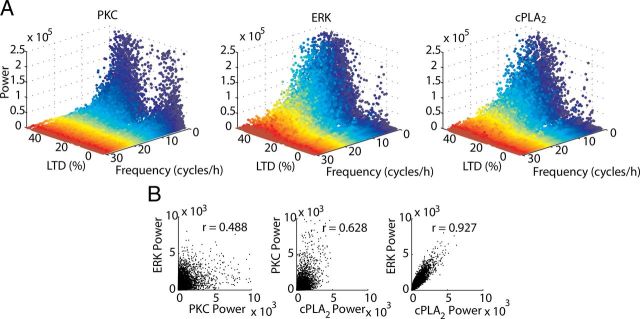
Discrete activity-dependent changes of NFs in the signaling network during LTD. A, LTD occurrence (LTD > 10%) promotes a small shift in the power of NFs of PKC and large shifts for the powers of NFs of ERK and cPLA₂, calculated for single runs of the model. B, Correlation between the powers of stochastic fluctuations is strong only between ERK and cPLA₂. In all panels, LTD was induced by Ca²⁺ pulses of 1–60 s and 0.5–3.5 μmol.L⁻¹.

Results

The model replicates macroscopic properties of LTD

Elevations of [Ca²⁺] induce LTD in PCs, measured as a reduction in the number of synaptic AMPARs in the model (Fig. 2A). The averaged curves of depression obtained with the model exhibit time courses in accordance with experimental data, reaching stable state ∼20 min after LTD induction (Tanaka and Augustine, 2008). During resting conditions, the model reproduces a number of AMPARs in accordance with values observed in a single synapse in PCs (Momiyama et al., 2003; Masugi-Tokita et al., 2007), and it also exhibits [Ca²⁺]-dependent levels of depression within the range of values typically observed experimentally (Fig. 2A) (Tanaka et al., 2007; Tanaka and Augustine, 2008).

A fundamental property of Ca²⁺-induced LTD is the sigmoidal relationship between the concentration of the triggering [Ca²⁺] and the magnitude of the depression (Tanaka et al., 2007), observed for mean results of several runs of the model (Fig. 2B) and described by Equation 1. Similar to experimental data (Tanaka et al., 2007), Ca²⁺ induces LTD in a highly cooperative manner (n_Hill ∼ 5–7) (Fig. 2C), and the level of change of the [Ca²⁺] required to trigger LTD is dynamically controlled by the duration of the Ca²⁺ pulses. Thus, increasing the duration of the [Ca²⁺] elevations shifts the sigmoid curves of LTD to the left (Fig. 2B), reflected by a decrease of K_1/2 (Fig. 2D) (Tanaka et al., 2007). However, the maximum depression observed is independent of the duration of the Ca²⁺ pulses tested (Fig. 2E) (Tanaka et al., 2007).

In single spines LTD is bistable and probabilistic

In contrast with mean results, single run results of the model show a strong bistability, with LTD induced in a completely all-or-none manner (Fig. 3A,B), which is also observed in other forms of synaptic plasticity (Petersen et al., 1998; O'Connor et al., 2005). Increasing the amplitude of the Ca²⁺ pulse reduces the number of failures of LTD induction (present in Fig. 3, A, but not in B) without changing the amplitude of successful induction. The magnitude of LTD obtained in a single run, which is equivalent to the occurrence of LTD in a single synapse, is independent of the duration and peak concentration of the triggering signal.

Figure 3.

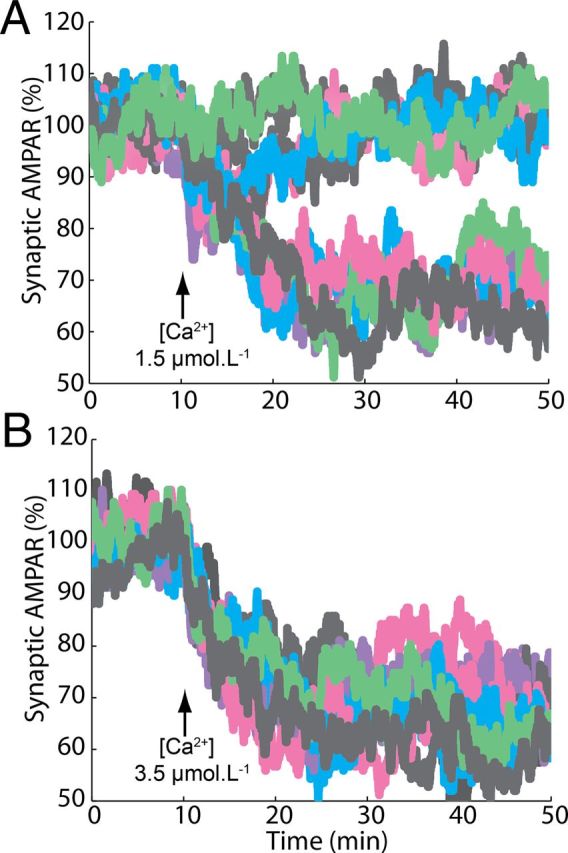
Bistable induction of LTD. A, B, Single run results of the model demonstrate that LTD in a single synapse is an all-or-none process. LTD was induced by pulses of 4 s and maximum [Ca²⁺] of 1.5 (A) and 3.5 μmol.L⁻¹ (B).

To understand how this property arises, we analyzed the activation of the most important components of the feedback loop in single runs of the model (Fig. 4A,B). The Ca²⁺ pulse causes a transient, direct activation of PKC and to a lesser degree of cPLA₂, proportional to the amplitude of the pulse. Note that the AMPA trafficking system filters out this rapid PKC transient, leading to the experimentally observed LTD induction curves (Fig. 4A,B, right panels). This filtering could not be observed in previous models (Kuroda et al., 2001; Tanaka et al., 2007) that only considered phosphorylated AMPAR as model output.

After the transient, PKC activation either returns slowly back to baseline and LTD fails (Fig. 4A,B, blue lines), or, sometimes after a delay, it continues to increase and LTD induction is successful (red lines). In the case of LTD induction, both ERK and cPLA₂ are also strongly activated, confirming the importance of the positive feedback loop. A critical property of this feedback loop is the ultrasensitivity of ERK activation, which requires dual phosphorylation happening in a two-collision mechanism (Huang and Ferrell, 1996) and determines its ability to respond strongly to suprathreshold inputs (Ferrell, 1996, 2002). These two structural properties, positive feedback loop and ultrasensitivity, filter small inputs and promote strong responses to suprathreshold stimuli (Ferrell, 1996, 2002), forcing the system to adopt one of two discrete stable states of activity (LTD and non-LTD).

Note that in Figure 4, A and B, each shows an example of Ca²⁺ inputs with the same magnitude that give rise to opposite responses in the model. This suggests that the induction of LTD has no fixed threshold for the input signals. Indeed, when the Ca²⁺ concentration (integrated over stimulus time to reduce noise) is plotted versus the amount of LTD obtained, the distributions for LTD and non-LTD overlap almost completely (Fig. 4C). Therefore, the induction of LTD in single spines is probabilistic, and its probability is modulated by the concentration and duration of the signal used to trigger it: inputs with higher peak concentration and longer duration are more likely to induce LTD than weak and brief signals (Fig. 4D), but there is no defined threshold. Such probabilistic behavior and threshold dithering are typical properties of biochemical systems undergoing inherent and unavoidable stochastic fluctuations or noise in their level of activity (Arkin et al., 1998; Rao et al., 2002; Simpson et al., 2009; Eldar and Elowitz, 2010).

Stochasticity influences the function of many systems, and it can have a variety of consequences. However, to understand its role during LTD occurrence, it is necessary to identify how it affects different parts of the signaling network. The absence of a fixed threshold extends to all components of the positive feedback loop tested (Fig. 4E). LTD can be triggered by a brief elevation of activity of any of these components, as observed experimentally (Tanaka and Augustine, 2008), but no thresholds can be discerned.

Next, we turned our attention to the pronounced stochastic fluctuations present in the activation of ERK and cPLA₂ (Fig. 4A,B) and characterized them qualitatively and quantitatively.

Stochastic fluctuation of activation of different components of the network

The qualitative analysis of the stochasticity of the signaling network was performed through analysis of the patterns of activation presented by different components of the model. The activation of the signaling network during LTD induction exhibits a pronounced variety of responses among its components. We focused our analysis on three components of the model belonging to three different legs of the positive feedback loop (PKC, ERK, and cPLA₂). When LTD induction is successful, PKC shows an overall constant activation with small magnitude fluctuations (Fig. 4A,B, red lines). Conversely, ERK activation presents high magnitude stochastic fluctuations without presenting a stable on-state, as reported previously (Bhalla, 2004a,b; Shankaran and Wiley, 2010). cPLA₂ follows a similar pattern of noncontinuous activation caused by intense stochastic fluctuations. These differences in activations are not caused by differences in the number of copies of the components of the model. PKC and ERK, for example, have similar population sizes (48 and 49 molecules, respectively), but exhibit distinct patterns of activation. Thus, these differences must be caused by specific reactions operating on each component of the model, which suggests that the stochastic fluctuations are transmitted nonuniformly through the network.

To characterize how the stochasticity is propagated, the CVs of all components of the feedback loop (Fig. 1A) were analyzed. The CV is a measure of noise, and it reflects how each component of the network amplifies or reduces, through its reaction mechanisms, the stochasticity of its upstream components. The change of the CV during LTD induction reveals that most components of the ERK cascade (Rafact, Raf, and MEK) present similar low levels of noise, but the CV of ERK is considerable higher (Fig. 5). Therefore, ERK is an important locus of stochasticity in the model, increasing abruptly the variability of responses in the network. This property arises from the ultrasensitivity of ERK (Ferrell, 1996, 2002), described above. The variability in ERK activation is especially high at the beginning of LTD occurrence, when the number of its activated molecules is usually low, adding more noise to its responses. ERK stochasticity is transmitted through the next two downstream components of the network, cPLA₂ and AA, respectively.

However, PKC, the next component of the feedback loop, filters considerable the noise and shows the lowest level CV of all components throughout. PKC activation, in contrast with the other components of the feedback loop, does not involve its phosphorylation catalyzed by other enzymes of the model. Instead, it depends on the interaction with second messengers, especially with AA. AA is responsible for the persisting activity of PKC during LTD occurrence after the level of Ca²⁺ has been restored to the resting concentration. To become fully activated, PKC requires high concentrations of AA (O'Flaherty et al., 2001), which has an important consequence in the model. The high AA concentration increases considerably the rate of the second-order reaction between AA and PKC, and, consequently, augments the rate of PKC activation without changing the rate of PKC inactivation, which is a first-order reaction. Thus, the activation of PKC by AA during LTD happens with a strong apparent affinity, which makes PKC activity less susceptible to undergoing high amplitude fluctuations.

To further characterize the fluctuations of the signaling network, power spectral analysis was used to estimate the noise frequency (NF) of the components during single runs of the model. Then, NF analysis was used to quantify how the different components interact with noise in the network. As expected from the results shown in Figure 4A, LTD promotes a strong shift in the power of the NFs of ERK and cPLA₂ but not for PKC (Fig. 6A). Instead, PKC always exhibits high power at slow frequencies (1–10 cycles/h) independent of the success of LTD (Fig. 6A). The pattern is very different for ERK and cPLA₂. In the absence of LTD (right part of the panels, centered ∼0%), very little NF power is present, significantly less than for PKC. But when LTD is successful (left side), these components show fluctuations with a larger variety of frequencies than PKC (1–30 cycles/h) (Fig. 6A). Moreover, the powers of the NFs of ERK and cPLA₂ are strongly correlated with each other, while the correlation of the powers of their NFs with that of PKC is much weaker (Fig. 6B). These results confirm that the stochasticity is nonuniformly transmitted within the feedback loop. The transmission of noise in a signaling network highly depends on the susceptibility of each downstream reaction to its upstream reaction (Paulsson, 2004). Our results demonstrate that the reactions involving cPLA₂ are very susceptible to the reactions of ERK and, consequently, these two enzymes exhibit similar frequencies and intensities of stochasticity. However, the pattern of activity of PKC differs strongly from these two components.

These results suggest that stochasticity can have distinct consequences for LTD occurrence, depending on the magnitude and frequency of the fluctuations and on the components that are affected. Strong stochastic fluctuations of PKC activation could be detrimental for LTD if they happen with high frequency and amplitude, because the feedback loop downstream of PKC may require prolonged and continuous stimulation. To test this hypothesis, we performed simulations where we introduced artificial perturbations of PKC activity in the model and observed that perturbations with strong intensities (Fig. 7A) or high frequencies (Fig. 7B) led to failure of LTD induction.

Figure 7.

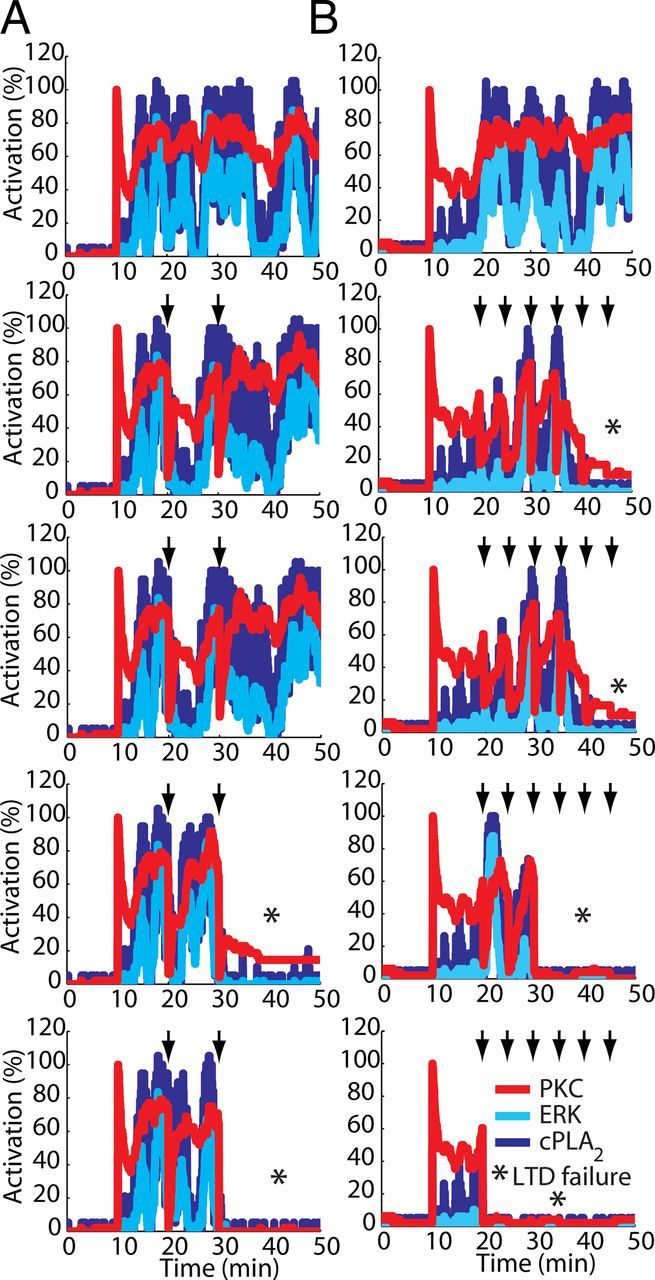
Detrimental effects of large fluctuations of PKC activity during LTD occurrence. Fluctuations in PKC activation are detrimental for the activation of the signaling network if they happen with high peak-to-peak amplitude fluctuations or with high frequency. Single runs of the model using equal seeds to initiate the simulations illustrate this detrimental effect. Each column (A, B) shows the results of simulations using the same seed. In these examples, a Ca²⁺ pulse of 4 s and peak concentration of 3.5 μmol.L⁻¹ applied at 10 min was used to induce the activation of the signaling network, and two (A) or six (B) transient perturbations (indicated by arrows) reducing PKC activity to a level varying from 80% to 0% of its activation (top to bottom) were applied. Each perturbation had a duration of 3 s. Both larger amplitude and high-frequency fluctuations in PKC activity negatively interfere with the activation of the signaling network, leading to failure of LTD (indicated by asterisks in the panel).

In contrast, the components downstream to ERK and cPLA₂ do not seem to require constant stimulation and respond effectively to large variations in the activity of their upstream signals. The permissivity of the components of the model downstream to ERK and cPLA₂ to a wide range of fluctuations of their activities is an important property of the signaling network of LTD. Thus, the stochasticity of ERK and cPLA₂ can modulate the probability of activation of the signaling network (Fig. 4D), without affecting downstream activity too much. This suggests that the system is making functional use of the stochastic fluctuations (Simpson et al., 2009; Eldar and Elowitz, 2010). To verify this hypothesis, we systematically manipulated the stochasticity of the signaling network.

Effect of biochemical population size

Stochastic fluctuations have a central role in many biochemical processes (Rao et al., 2002; Simpson and Cummings, 2011), and are caused mainly by small number of molecules (Simpson et al., 2009). Therefore, alterations in the population size of a given system are a good way to manipulate noise and address its role (Bhalla, 2004a,b). Most species of the model have populations with <50 copies (Peng et al., 2004; Cheng et al., 2006; Sheng and Hoogenraad, 2007). Thus, to investigate the role of the stochasticity during LTD, the biochemical population size (BPS) was systematically altered. For each component analyzed, the BPS regulates the overlap between the levels of its activity triggered by Ca²⁺ inputs with different magnitude (Fig. 8A). For the standard model (BPS₁), there is no clear threshold for activation of any of the network components analyzed; this is comparable to Figure 4C where a similar lack of threshold for LTD induction was shown. Increasing the BPS gradually reduces the overlap of responses leading to the appearance of a clear threshold from BPS₁₆ on (Fig. 8A). Conversely, lowering the BPS increases the overlap and for BPS_0.2 the distributions are almost symmetric.

The BPS also controls the magnitude and width of the stochastic fluctuations in the signaling network (Fig. 8B). Increasing the BPS decreases the amplitude and frequency of the stochastic fluctuations and diminishes the probability of LTD induction to weak or intermediary inputs. It reduces the NFs in trials with successful LTD induction (Fig. 8B) and greatly increases the correlation of the powers of NFs of stochastic fluctuations between PKC and ERK from 0.488 (BPS₁) to 0.762 (BPS₁₂₈) and between PKC and cPLA₂ from 0.628 to 0.813, making the behavior of different components of the network more homogeneous. The slower fluctuations strengthen the activation of the feedback loop (Weinberger et al., 2008), avoiding the failure of LTD induction to suprathreshold inputs and contributing to the appearance of a clear threshold in the input signal. Conversely, reducing the BPS amplifies the magnitude and frequency of stochastic fluctuations even before the input signal has been applied, causing the network to exhibit spontaneous activation.

The alterations in the signaling network caused by increasing the BPS reduce the variability of the mean LTD curves, causing the loss of stable and persistent intermediary depressions and converging the model to a bistable system (Fig. 9A). The reduction of the stochastic fluctuations improves the filtering of small inputs and increases the responses to suprathreshold inputs. As a consequence, the behavior of the stochastic model with large BPS becomes very similar to the deterministic version of the model (Fig. 9E). Conversely, decreasing the BPS increases the stochasticity of the signaling network, which increases the probability of LTD induction in absence of input, causing the loss of stable weak and intermediary levels of depression and moving the model to a monostable system (always LTD, Fig. 9A).

These changes can be further analyzed by fitting sigmoidal curves (Eq. 1) relating LTD amplitude to the peak concentration of the Ca²⁺ pulses used to trigger it (Fig. 9B). Changes of the BPS lead to a great alteration in the cooperativity (n_Hill) observed for Ca²⁺ during LTD induction (Fig. 9C), but only to a small alteration in the Ca²⁺ requirement (K_1/2) (Fig. 9D).

The combined results of Figures 8 and 9 demonstrate the importance of threshold dithering and stochastic fluctuations for attaining the normal macroscopic behavior of the system. They also indicate that there is an optimum level of stochasticity in the signaling network of LTD, which is obtained around BPS₁. This level of stochasticity allows the system to have a macroscopic stable off-state and an extensive variety of stable macroscopic on-states (Tanaka et al., 2007).

Discussion

Stochastic model of cerebellar LTD

Our model builds on previous work that simulated the PKC-ERK-cPLA₂ positive feedback loop (Bhalla and Iyengar, 1999; Kuroda et al., 2001), but expands it in several aspects. First, many reaction parameters were updated according to recent literature and several additional reactions were included. Next, an AMPAR trafficking model was added, which allowed for direct comparison with experimental data. Previous models used the concentration of phosphorylated AMPARs as an LTD measure (Kuroda et al., 2001; Tanaka et al., 2007). However, there is no indication that this measures LTD (Linden, 2001). In fact, some phosphorylated AMPARs remains in the postsynaptic membrane during depression (Chung et al., 2000; States et al., 2008), because AMPAR phosphorylation promotes a reduction but not the complete loss of affinity for GRIP (Matsuda et al., 1999, 2000).

The most important difference between our model and previous ones is, however, the use of stochastic simulation methods. Despite the small numbers of molecules present in dendritic spines (Sheng and Hoogenraad, 2007), most models of long-term synaptic plasticity are deterministic (Kotaleski and Blackwell, 2010). We clearly demonstrate the importance of stochastic simulation because the deterministic solution of the same model leads to substantially different results, namely a bistable system with strong thresholds.

The model was tuned to reproduce with good accuracy many experimental properties of cerebellar LTD. It matches qualitative characteristics (time course of LTD, sigmoidal relationship between Ca²⁺ and the depression), but also quantitative results (n_Hill, K_1/2, LTD_max) (Momiyama et al., 2003; Masugi-Tokita et al., 2007; Tanaka et al., 2007; Tanaka and Augustine, 2008). The quantitative characterization of the relation between Ca²⁺ and synaptic plasticity (Tanaka et al., 2007) is unique in the literature and provided strong constraints. However, these data reflect the response of hundreds of PC spines to the uncaging signal and is therefore only relevant toward the mean response of the model. We have assumed that reactions in single spines are independent of those in nearby spines and can be simulated as separate runs of the model, but it cannot be excluded that spatial chemical gradients within the dendrite (Schmidt and Eilers, 2009) cause correlations between spines.

LTD induction is bistable and probabilistic

An important prediction of the model is that LTD induction in a single PF-PC synapse is an all-or-none process, as in other forms of long-term synaptic plasticity (Petersen et al., 1998; O'Connor et al., 2005). Commonly, bistability is observed in cellular processes that should present the same pattern of responses under different environmental conditions (Ferrell, 1996). Maximal LTD involves a decrease of 30–50% of postsynaptic current, which suggests a similar reduction in the number of synaptic AMPARs (Matsuda et al., 2000; Linden, 2001). This number ranges ∼80–140 U in a single PF-PC synapse (Momiyama et al., 2003; Masugi-Tokita et al., 2007), while the number of copies of most components of the spine signaling network is <50. In such a system, graded changes in the number of synaptic AMPARs in a single synapse, especially weak and medium ones, are likely to be dispersed by stochastic fluctuations. Therefore, a switch-like occurrence of LTD in spines can be important to avoid undetectable responses and to guarantee that depression in unitary synapses is sufficiently strong to be efficiently integrated by the neuron.

A second and major prediction is that the induction of LTD is probabilistic. Consequently, equal inputs can promote opposite responses (LTD and non-LTD). Recently, several studies have attempted to identify thresholds in the input signal to induce LTD and LTP (Jörntell and Hansel, 2006; Vogt and Canepari, 2010). Our findings do not invalidate these results when a population of synapses is considered. However, we demonstrate a mismatch between the macroscopic and microscopic Ca²⁺ requirement for LTD induction. An input threshold can be identified for the induction of strong LTD in a population of synapses (indicated by the K_1/2), but when single synapses are considered, the intensity of the Ca²⁺ signals only regulates the probability of induction. The history of each synapse may be crucial in modulating this probability (Doi et al., 2005; Wang et al., 2005).

The probabilistic nature of LTD induction has important consequences for experiments studying synaptic plasticity: in single spine Ca²⁺ imaging (Higley and Sabatini, 2008) there is no threshold that definitely predicts the occurrence of plasticity. Moreover, although we do not simulate cerebellar LTP, our results imply that, in spines where bidirectional forms of synaptic plasticity depend on the level of change of [Ca²⁺], inputs with the same magnitude can probably cause three different responses (LTD, LTP, and no alteration).

Probabilistic events are important to synaptic physiology (Kennedy et al., 2005; Ribrault et al., 2011) and we show that LTD induction in single synapses is also probabilistic. The combination of two characteristics, bistable and probabilistic induction of LTD, is sufficient to generate macroscopic curves of depression matching experimental data. Moreover, the probabilistic nature of LTD induction is not caused by the stochasticity of the Ca²⁺ input signal as suggested previously in PCs (Tanaka et al., 2007) and other systems (Graupner and Brunel, 2007), but rather by stochastic fluctuations affecting the level of activity of most components of the signaling network.

Functional role of nonuniform stochastic fluctuations

Noise in cellular processes is caused by the discrete nature of their biochemical populations and reactions. Noise fluctuations are important in small systems such as spines, where their magnitude can exceed or approach the mean values of the state variables (Simpson et al., 2009) and trigger responses for inputs that are filtered in a deterministic system. Noise can provide probabilistic selection of signaling pathways, generate differentiation strategies, enable physiological mechanisms, coordinate the expression of genes, and facilitate evolutionary adaptation (Arkin et al., 1998; Rao et al., 2002; Raser and O'Shea, 2005; Weinberger et al., 2008; Simpson et al., 2009; Eldar and Elowitz, 2010). For LTD, noise affecting the level of activity of the network determines the probabilistic induction in single synapses and causes threshold dithering, producing variability of stable macroscopic responses. Because of the large number of PF synapses onto a PC (∼175,000) (Napper and Harvey, 1988), it is reasonable to expect that synaptic LTD induction protocols will activate hundreds of them (Steuber et al., 2007). While single runs of the model are totally binary, the macroscopic behavior of the model is described by sigmoid curves with n_Hill ranging from 5 to 7. Therefore, the network of LTD is using stochastic fluctuations to increase the dynamic range of its macroscopic responses, similar to other systems (Simpson et al., 2009).

Unexpectedly, stochastic fluctuations affect the activity of the components of the network nonuniformly: while some components fluctuate intensely, others present a more continuous pattern of activity. Similarly, mammalian genes are transcribed with a wide range of specific bursting kinetics (Suter et al., 2011), which suggests that nonuniformly distributed stochasticity might be an important property for cellular processes. Many factors can determine how each biochemical component is affected by stochastic fluctuations. Molecules presenting slow binding and unbinding kinetics during complex formation, strong interactions, or interactions with multiple steps are less likely to undergo intense and brief fluctuations. Contrarily, ultrasensitive or cooperative molecules such as ERK greatly amplify small changes of their upstream signals (Ferrell, 1996; Huang and Ferrell, 1996), making them important loci of variability. It would be interesting to verify whether MAPK pathways present in other forms of synaptic plasticity act similarly and how noise propagates in signaling networks exhibiting cross talk among different ultrasensitive molecules, because the ultrasensitivities of different components within a cascade combine multiplicatively (Ferrell, 1996).

However, to make functional use of noise, a signaling network requires not only a good source of variation of responses, but it must also have components capable of responding to these variations. In the LTD network, ERK acts as an important source of variability; cPLA₂ and AA follow similar patterns. Contrarily, PKC filters the highly fluctuating activity of its upstream signals, but it responds to it and robustly transmits the filtered responses to its downstream components, including the AMPARs that express the physiological effect of LTD.

Effect of biochemical population size

Changes in the level of stochasticity of the model greatly alter its properties. Reducing the noise by increasing the BPS improves filtering of weak inputs and responses to suprathreshold signals by strengthening the feedback loop activation (Weinberger et al., 2008). This causes the appearance of a clear threshold in the LTD input signal and changes the behavior of the model from probabilistic to deterministic. As a result, macroscopic responses for larger BPSs are highly cooperative and more similar to the responses obtained in single runs. Decreasing the BPS increases stochasticity and causes a very different outcome by promoting the induction of spontaneous LTD. Consequently, our results indicate an ideal level of stochasticity that can be functionally used to increase the variability of macroscopic responses during LTD. The actual variability in PC spine head volume is quite restricted (a factor three range in sizes) (Harris and Stevens, 1988; Vecellio et al., 2000), suggesting that BPS may be closely regulated in this system.