Figure 4.

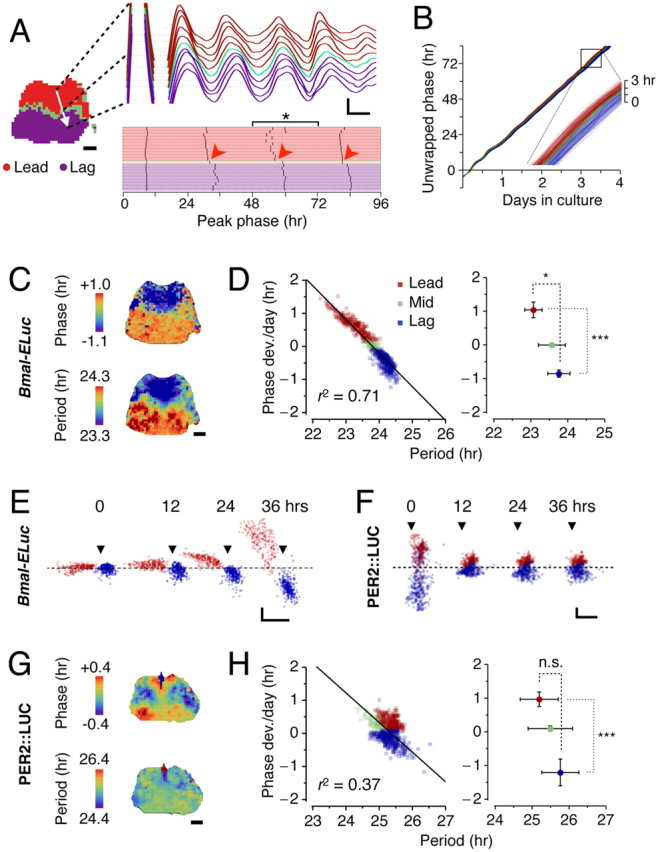
Clustering of correlated Bmal1 oscillations originates from period heterogeneity. A, Along a path from one cluster to the other (white arrow, left), correlation in oscillatory activities of Bmal1 in the neighbors sharply drops as the path crosses the border between the leading and the lagging clusters (top right), which results in disjoints (arrowheads) in positions of peak phase (bottom right). The scale bar of the slice image is 100 μm here and throughout. The calibration of the detrended oscillations represents 12 h (x-axis) and 10 bits of detrended bioluminescence (y-axis). B, The continuous phase evolution over time is illustrated by unwrapped phases that are highly linear (r² = 0.998 ± 0.002, mean ± SD; for n = 700 grids in the present sample; r² = 0.993 ± 0.009 in n = 23 explants), indicating the phase increases at a constant rate. The oscillators belonging to the phase-leading cluster (red) consistently have higher slopes than the ones in the phase-lagging cluster (blue) (inset magnifies the boxed, which spans 12 h in culture). C, The phase distribution (top) is markedly discrete throughout the SCN. Shown are the peak phases on the third day in culture (bracketed in A, *). The period distribution (bottom) exhibits discrete spatial patterning. D, Left, The time average of phase deviation shows a strong negative linear relationship with intrinsic periods (r = −0.84; p < 0.001 in the present sample), and the relationship is predicted by linearization of the mean period (coefficient of determination as goodness of fit, r² = 0.71) (solid line). D, Right, In Bmal1 oscillations, the leading and lagging clusters are resolved by both periods (*p < 0.05) and phase (***p < 0.001). E, Over time in culture, phase of each Bmal1 oscillator (y-axis) gradually moves away from the mean according to its intrinsic period (x-axis). Snapshots of phase versus period are shown at 0, 12, 24, 36 h in culture. The arrowheads indicate where the period equals 24 h, and the dashed line shows where the phase deviation is zero. The x- and y-axis calibrations represent 1 h, here and in F. This illustrates that the intrinsic period is the origin of tight correlation between the phase and the period. F, In Per2 oscillators, the gradual separation of phase is not evident. The arrowheads indicate where the period equals 25 h. G, Clustered Per2 oscillations is reflected in the discrete spatial phase distribution (top) but not in period (bottom). H, The leading (red) and lagging (blue) clusters are separated by phase but not by period; the relationship between phase and period is not clearly linear (r² = 0.37) (left). In all Per2 samples, the leading and lagging clusters are not resolved by period (p = 0.22, n = 8) but by phase (***p < 0.001) (right).