Skip to main content
. 2011 Apr 6;31(14):5365–5377. doi: 10.1523/JNEUROSCI.6472-10.2011

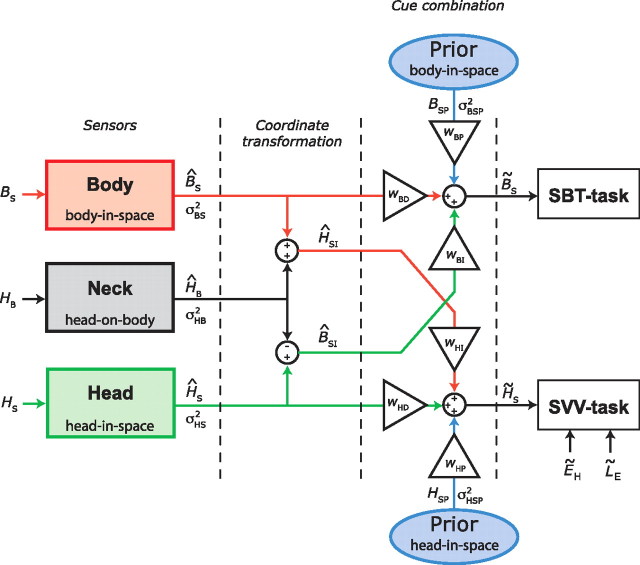
Figure 1.

Figure 1.

Schematic representation of the sensory integration model. Sensory signals, denoted by a hat symbol (∧), are assumed to be calibrated accurately, but contaminated by Gaussian noise. Optimal estimates are denoted by a tilde (∼). Body sensors, neck sensors, and otoliths provide information about orientation of body in space (BS), head on body (HB), and head in space (HS), respectively. Neck signal (ĤB) is used for a reference frame transformation of otolith information into a body-in-space signal (ĤS − ĤB = B̂SI), and for a transformation of body-tilt information into a head-in-space signal (B̂S + ĤB = ĤSI). For an optimal estimate of body-in-space orientation, B̃S (SBT task), the model combines the body-sensor signal (B̂S, red pathway) with a reference-frame-transformed otolith signal (B̂SI, green pathway). Relative contributions of the two pathways (wBD and wBI) depend on their relative precision (Eq. 2). The scheme shows a symmetrical arrangement with two priors, but there is ample reason to believe that their effects are not identical. The simplest explanation of current and previous SBT data (see Materials and Methods, SBT computation) indicates that the associated prior in this task is uniform, which implies that wBP can be ignored. In the SVV task, an optimal estimate of head-in-space (H̃S) is obtained by integration of otolith information (ĤS, green pathway), reference-frame-transformed information from body sensors (ĤSI, red pathway), and a significant contribution from prior information (HSP, blue pathway). Relative weights are denoted by wHD, wHI, and wHP, respectively. Estimate of line-in-space orientation is obtained by combining H̃S and estimates of eye-in-head (ẼH) and line-on-eye (L̃E) orientation. Noise variance in body sensors (σBS2), neck sensors (σHB2), otoliths (σHS2), and width of prior (σHSP2) defines their relative weights (see Materials and Methods). Otolith noise may depend on tilt angle (Eq. 11). Note that the process of sensory integration, denoted here by summation of weighted sensory signals, is equivalent to multiplication of the underlying probability distributions (Eqs. 2 and 6 and Appendix).