Gain Field Encoding of the Kinematics of Both Arms in the Internal Model Enables Flexible Bimanual Action

Abstract

Bimanual action requires the neural controller (internal model) for each arm to predictively compensate for mechanical interactions resulting from movement of both that arm and its counterpart on the opposite side of the body. Here, we demonstrate that the brain may accomplish this by constructing the internal model with primitives multiplicatively encoding information from the kinematics of both arms. We had human participants adapt to a novel force field imposed on one arm while both arms were moving in particular directions and examined the generalization pattern of motor learning when changing the movement directions of both arms. The generalization pattern was consistent with the pattern predicted from the multiplicative encoding scheme. As proposed by previous theoretical studies, the strength of multiplicative encoding was manifested in the observation that participants could adapt reaching movements to complicated force fields depending nonlinearly on the movement directions of both arms. These results indicate that multiplicative neuronal influence of the kinematics of the opposing arm on the internal models enables the brain to control bimanual movement by providing great flexible ability to handle arbitrary dynamical environments resulting from the interactions of both arms.

Introduction

One of the unsolved problems in motor control science is how the brain orchestrates the movement of multiple body parts as a unified action (e.g., bimanual movement). Previous studies of unimanual reaching movement have suggested that the brain accomplishes flexible movements by constructing an “internal model” of the dynamic properties of the body and the environment (Kawato, 1989; Bhushan and Shadmehr, 1999). It was also suggested that humans build these internal models through a flexible combination of motor primitives encoding the kinematics of the desired arm (Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Sing et al., 2009). However, this powerful scheme is not directly compatible with control of bimanual movement. When we perform bimanual movements such as manipulating an object, every movement of each arm disturbs the other arm because the dynamics of both arms are coupled through the object and the person's body. Therefore, the desired motor command for each arm cannot be determined solely by the state of the arm itself, which may not be explained by the conventional scheme of primitives. One solution is to assume that an additional neuronal process adjusts the motor command by estimating the interaction; however, this may create another question regarding how this additional process is implemented in the brain.

An alternative is to assume, as we have done here, that the primitives of the internal model encode not only the desired kinematics of the relevant arm but also those of the opposite arm. This proposal is based on recent reports that distinct internal models can be constructed depending on the kinematics of the opposite arm (Nozaki et al., 2006; Nozaki and Scott, 2009; Howard et al., 2010). According to this assumption, the process of constructing an internal model for one arm with primitives can be formulated as f̂ = w^tg(x_r, x_l), where f̂ is a force output, w = (w₁, w₂,… )^t is a weight vector, and g = (g₁(x_r, x_l), g₂(x_r, x_l),… )^t is a vector whose elements represent the output of each primitive; x_r and x_l represent the kinematics of the right and left arm, respectively.

From this viewpoint, the ability of the brain to accomplish flexible bimanual movement can be regarded as the ability to construct flexible force output by combining the primitives. How, then, should the primitives encode the kinematics of both arms? Previous theoretical works (Pouget and Sejnowski, 1997; Salinas and Sejnowski, 2001) have provided a clue. They proposed that neurons encoding two inputs, x₁ and x₂, multiplicatively [h(x₁, x₂); “gain field” encoding (Andersen and Mountcastle, 1983; Andersen et al., 1985)] work as a set of basis functions enabling downstream neurons to construct the arbitrary output function y(x₁, x₂) = w^th(x₁, x₂). This close similarity to the current problem led us to further hypothesize that multiplicative encoding of the kinematics of both arms in the primitives enables the brain to create an arbitrary force output. We tested this hypothesis by examining the generalization pattern of motor learning (Shadmehr and Mussa-Ivaldi, 1994; Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Hwang et al., 2003; Sing et al., 2009), which should reflect the encoding structure in the primitives (Hwang et al., 2003; Wainscott et al., 2005).

Materials and Methods

Participants.

Thirty-six healthy right-handed volunteers (aged 18–31 years; 12 women) participated in our study after providing written informed consent. All experimental procedures were approved by the ethics committee of the Graduate School of Education, The University of Tokyo.

General task settings.

The participants were asked to make simultaneous center-out bimanual reaching movements (see Fig. 1A), with a movement amplitude of 8 cm and a duration of 400 ms, holding the handles of two robotic manipulanda (Phantom 1.5 HF; SensAble Technologies). Throughout the experiment, the position of each handle was always visible as a white cursor (diameter, 6 mm) on a horizontal screen over the handles. The movements of the handles were constrained to a virtual horizontal plane implemented by a simulated spring (1.0 kN/m) and dumper [0.1 N/(m/s)]. Wrist braces were used to reduce unwanted wrist movements. The participants' upper arms were supported by arm slings to reduce fatigue and allow maintenance of a constant arm posture.

Figure 1.

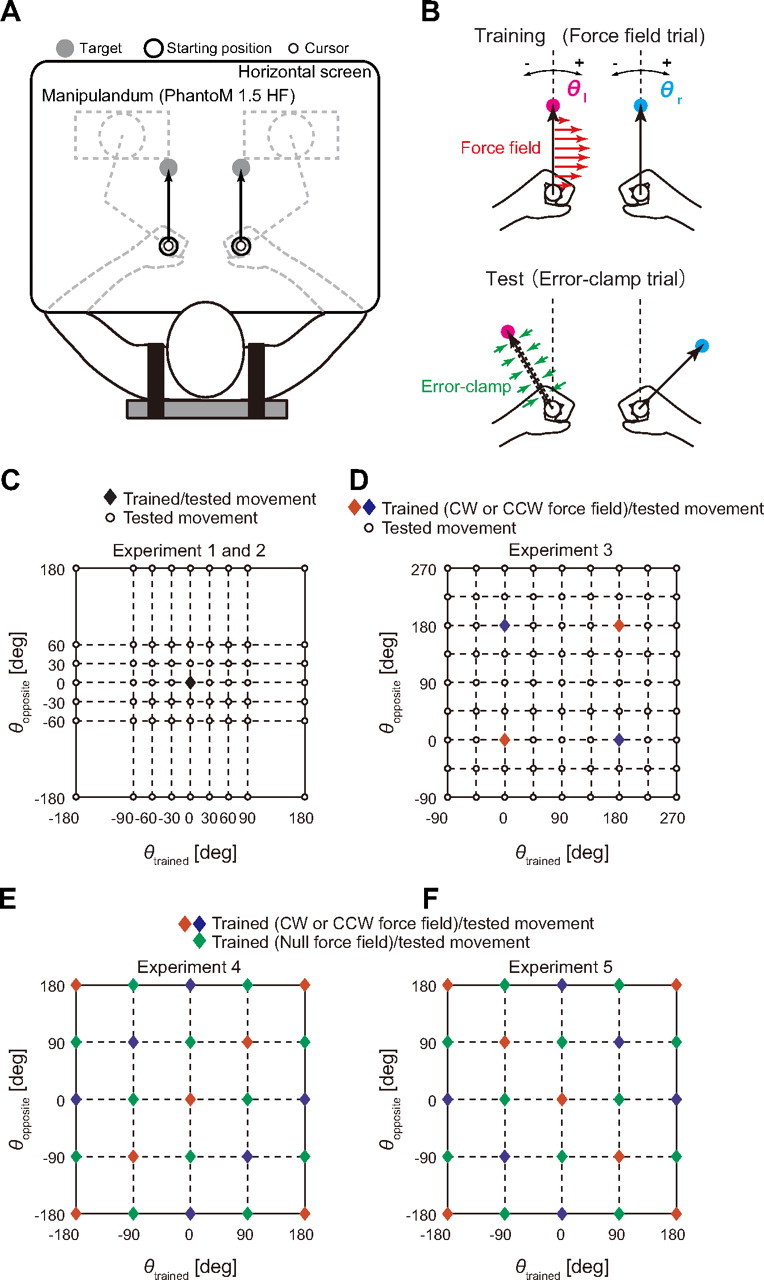
Experimental setup. A, The participants made simultaneous bimanual reaching movements from the starting point toward a peripheral target for each arm presented on a horizontal screen. B, A force field was applied to the participants' trained arm for the training (top panel). Error-clamped trials were alternated with standard trials to test the degree of motor adaptation (bottom panel). The movement direction toward a forward target was defined as 0°, and the movements in clockwise (CW) and counterclockwise (CCW) directions were positive and negative, respectively. C–F, Movement configurations for the training and testing trials. The diamonds indicate the movement configurations used for the training, while the open circles indicate the movement configurations for which the training effect was tested. For example, in Experiments 1 and 2 (C), participants learned the force field for the trained arm while moving both arms forward, as indicated by the diamond [(θ_trained, θ_opposite) = (0, 0)]. This training effect was then tested at the other movement configurations represented by open circles [e.g., (θ_trained, θ_opposite) = (30, 60)]. In D–F, the color of the diamonds indicate the kind of force field: blue and red indicate CW and CCW force fields, respectively (the direction of force field was reversed for one-half of participants), and the green diamond indicates a null force field. It should be noted that several tested configurations are plotted twice [e.g., (180, 180) and (−180, −180) in C, and (−90, −90) and (270, 270) in D]. It should also be noted that unimanual movements were also tested in Experiments 1 and 2, but these movements are not displayed in B.

Initially, the participants were required to move each cursor into its home position (diameter, 10 mm; the distance between the starting positions was 20 cm). After a 2 s holding time, a gray target (diameter, 10 mm) appeared for each hand in each position. The “go” cue, a color change and “beep” sound, was provided after a further random holding time (1–2 s). A warning message was presented on the screen if the movement speed of either handle was above (“Fast”) or below (“Slow”) a target range of 376 ± 56.4 mm/s. At the end of each trial, the handle of each manipulandum automatically returned to its home position. The motion data for each manipulandum were recorded at a sampling rate of 500 Hz. The data for the handle velocity and force were low-pass filtered using a fourth-order Butterworth filter with a cutoff frequency of 8 Hz.

Evaluation of motor performance.

We had participants adapt to a novel force field during bimanual reaching movements (see Fig. 1B; see the following sections for further details). To quantify the degree of motor adaptation when changing movement directions of both arms (see Fig. 1B for the definition of “movement direction”), we used the “error-clamp” method (Scheidt et al., 2000; Smith et al., 2006; Sing et al., 2009). During error-clamped trials, the trajectory of the handle was constrained to a straight line toward the target by a virtual “channel” (see Fig. 1B) in which any motion perpendicular to the target direction was constrained by a one-dimensional spring (2.5 kN/m) and damper [25 N/(m/s)]. This method enabled us to measure directly the lateral force exerted toward the channel; the difference between this lateral force at the peak velocity and that from the baseline session was used as the aftereffect of learning. To quantify performance in trials where the error-clamp method was not adopted (e.g., trials in the training phase), we quantified the lateral deviation of each handle trajectory at the peak velocity from a straight line between the starting position and target.

Experiments 1 and 2.

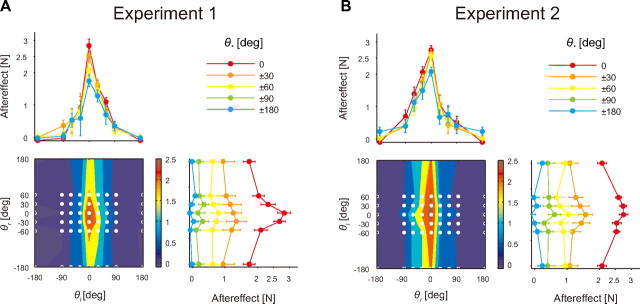
Experiments 1 and 2 (N = 8 apiece) were designed to investigate how the adaptation of one arm (left arm in Experiment 1 and right arm in Experiment 2) to a novel force field acquired while reaching both arms forward was transferred to the same arm when the movement directions of both arms were changed (8 directions for the trained arm, and 6 directions for the opposite arm [i.e., 48 (=8 × 6) combinations]; see Fig. 1C). Participants also performed unimanual reaching movements in eight directions.

The experiment was composed of 280 trials in the baseline session, 80 trials in the training session, and 463 trials in the testing session. Experiments 3–5 also consisted of these three sessions (Table 1). During the baseline session, each pattern of 56 combinations of movement directions for both arms (48 and 8 bimanual and unimanual movement patterns, respectively) was performed in a randomized order within each cycle; thus, every movement configuration was performed in a single cycle. The first 112 trials were composed of null force field trials, and the subsequent 168 trials were composed of error-clamped trials. During the training session, participants moved both arms forward and a velocity-dependent rotational force field was applied on one arm as f = Bv, where f = (f_x, f_y)^t is the force to the handle of the trained arm (N), v = (v_x, v_y)^t is the velocity of the handle (m/s), and B is the viscosity matrix [N/(m/s)]. To cancel out the biomechanical effect of the force direction, the direction was reversed for one-half of the participants, as B = [0 −10; 10 0] or B = [0 10; −10 0]. During the testing sessions, in addition to the force field trials with both arms reaching forward, every other trial was a catch trial (error-clamped trials), allowing quantification of the aftereffects of the training trials. The order of the 56 movement patterns was randomized within each of the four cycles.

Table 1.

Experimental conditions

Experiment	Trained arm	Movement configuration		Trial number
		Training	Baseline/test	Baseline	Training	Test
Experiment 1 (N = 8)	Left	1	48	280	80	463
Experiment 2 (N = 8)	Right
Experiment 3 (N = 10)	Left	4	64	192	160	399
Experiment 4 (N = 5)	Left	16	16	144	960	192
Experiment 5 (N = 5)	Left

Experiment 3.

In Experiments 1 and 2, only one movement configuration was adopted for the training. Experiment 3 was designed to examine how participants adapt to a force field when they are trained at multiple movement configurations and how the learning effect can be generalized to the other movement configurations. We also used the data to evaluate how accurately the mathematical models identified in Experiment 1 (described later) can predict the aftereffects.

Ten participants trained with the same force field used in Experiment 1 for four different movement combinations: (θ_r, θ_l) = (0°, 0°), (0, 180), (180, 0), and (180, 180) (see Fig. 1D). The direction of the force field was reversed between the parallel [(θ_r, θ_l) = (0°, 0°), (180, 180)] and opposite [(θ_r, θ_l) = (180°, 0°), (0, 180)] movement patterns. The experiment consisted of 192 trials for the baseline session, 160 trials for the learning session, and 399 trials for the testing session (total = 751 trials). In the baseline session, 64 movement patterns (eight directions for each arm: θ_l = −135, −90, −45, 0, 45, 90, 135, 180°, and θ_r = −135, −90, −45, 0, 45, 90, 135, 180°) were adopted. Subsequent to the 64 null force field trials, 128 error-clamped trials were performed for the baseline session (two cycles). After the learning session of four movement patterns (40 cycles), in the testing session, the force field trials of the four movement patterns and catch trials (i.e., error-clamp trials) of the 64 movement patterns (see Fig. 1D) were performed alternately (three cycles). Movement patterns were performed in a randomized order within a single cycle for all sessions.

Experiments 4 and 5.

Experiments 4 and 5 were designed to investigate whether participants could adapt their arm movements to more complicated dynamic force fields that change nonlinearly with the kinematics of both arms. The participants (N = 5 for each experiment) attempted to adapt their left arm movement to a velocity-dependent rotational force field, the magnitude of which depended nonlinearly on the movement directions of both arms as f_exp4 = cos(θ_l − θ_r)Bv (Experiment 4) and f_exp5 = cos(θ_l + θ_r)Bv (Experiment 5). The direction of the force fields was reversed for two of five participants. Regarding f_exp4, the relative difference in the movement directions between both arms determines the direction of the force field. As long as the movement directions of both arms are the same in the extrinsic workspace, the direction of the force field to the left arm is identical; the force direction reverses when both arms move in the opposite direction. However, in f_exp5, as long as the movements of both arms are mirror symmetric (i.e., the same direction with respect to the joint or intrinsic workspace), the direction of force field to the left arm is identical; however, this force reverses direction when both arms move in the opposite direction in the intrinsic workspace.

The experiments consisted of 144 trials for the baseline session, 960 trials for the learning session, and 192 trials for the testing session (total = 1296 trials). Participants were asked to reach in 16 movement configurations (θ_l = −90, 0, 90, 180°, and θ_r = −90, 0, 90, 180°) for all sessions. In the baseline session, the error-clamped trials were randomly conducted once every three trials (three cycles). In the learning session (40 cycles), 16 movement patterns were randomly performed within each cycle; to effectively promote learning, the number of trials with force was twice that of trials with null force. In the testing session, in addition to the force field trials performed the same as in the training session, catch trials (error-clamped trials) were performed once in every four trials (three cycles), and the order of the movement patterns was randomized within each cycle.

Theoretical background.

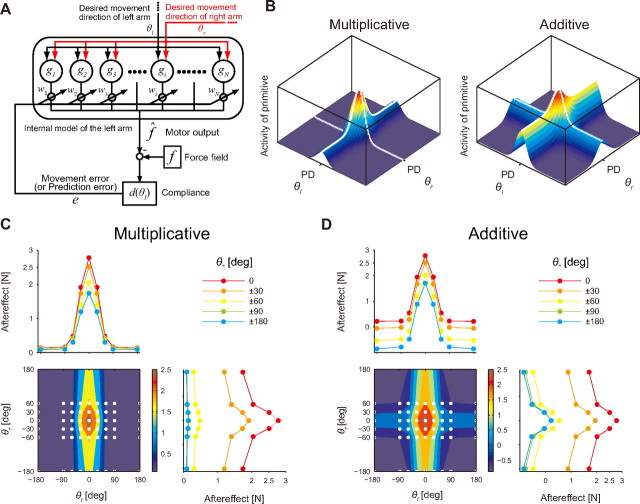
We modeled the motor learning process using the state space model (Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Wainscott et al., 2005; Lee and Schweighofer, 2009; Nozaki and Scott, 2009), consisting of N primitives that encode the movement directions of both arms as g(θ_r, θ_l), where θ_r and θ_l are the movement directions of the right and left arms, respectively (see Fig. 3A). The output force created by the internal model can be represented by a linear summation of the outputs of primitives as follows:

where i is the trial number, and g(θ_r, θ_l) = [g₁(θ_r, θ_l), g₂(θ_r, θ_l),… g_N(θ_r, θ_l)]^t and w = [w₁, w₂,… w_N]^t are column vectors whose elements represent the output and weight of each primitive, respectively.

Figure 3.

State space model for motor learning. A, We assumed that the internal model for the left arm was composed of N primitives [g = (g₁, g₂, … , g_N)^t] for motor learning that receive the signals of desired movement directions of both arms (θ_r, θ_l). The contribution of each primitive [w = (w₁, w₂, … , w_N)^t] to net output (^f) was updated trial-by-trial according to the movement error (e). B, The response of a primitive with multiplicative (left) or additive (right) encoding predicted from the data shown in Figure 2, D and E. C, D, Simulated generalization patterns for multiplicative encoding (C) and additive encoding (D). Bottom left, Contour plot of the generalization pattern. The color bar indicates the magnitude of the model output (i.e., aftereffect). The white dots indicate the movement configurations at which the aftereffects were measured. Top left, Generalization curve (aftereffect vs θ_l). Bottom right, Generalization curve (aftereffect vs θ_r).

A state space model of the motor adaptation to the force field f can be represented as follows:

where e is the movement error, d(θ_l) is the compliance that depends on the movement direction of the trained arm (here, we assumed that the left arm is trained), and α and K are constants representing, respectively, the spontaneous loss of memory and the update rate to the error.

From Equations 1–3, the weight vector after sufficient training of a constant force field f is obtained as follows:

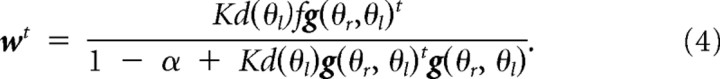When movement directions of both arms are changed by Δθ_r and Δθ_l, the force output (i.e., aftereffect) is represented as follows: f̂(θ_r + Δθ_r, θ_l + Δθ_l) = w^tg(θ_r + Δθ_r, θ_l + Δθ_l). Thus, the function of how the training effect is transferred from (θ_r, θ_l) to (θ_r + Δθ_r, θ_l + Δθ_l) is represented by the following:

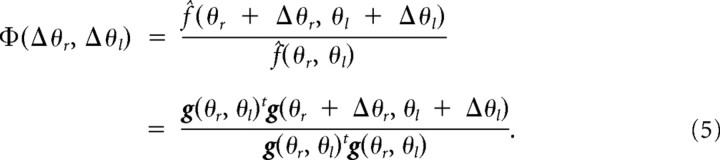Decomposition of the generalization function.

If the primitives encode the movement directions of both hands multiplicatively as follows: g_j(θ_r, θ_l) = r_j(θ_r)l_j(θ_l), when N is sufficiently large (N is assumed to be a square number), and l_j(θ_l) and r_j(θ_r) have translational symmetry with respect to j and are distributed uniformly on the (θ_r, θ_l) plane, then

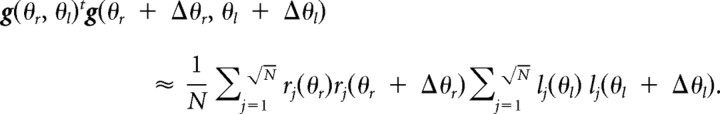Thus, the transfer function is as follows:

On the other hand, if the primitives encode the movement directions of both hands additively as follows: g_j(θ_r, θ_l) = r_j(θ_r) + l_j(θ_l), then g(θ_r, θ_l)^tg(θ_r+Δθ_r, θ_l+Δθ_l) = Σ_j=1^N[r_j(θ_r)+l_j(θ_l)] {[r_j(θ_r + Δθ_r) + l_j(θ_l)]+[r_j(θ_r)+l_j(θ_l+Δθ_l)]−[r_j(θ_r)+l_j(θ_l)]}. Thus, the transfer function is as follows:

It should be noted that previous work (Wainscott et al., 2005) obtained theoretically similar relationships (Eqs. 6, 7) in the generalization function calculated from the trial-by-trial changes in the aftereffects.

Estimating the function of the primitives.

Here, we assume that the encoding function can be represented by a Gaussian function. In the case of multiplicative and additive encoding, the primitive can be represented, respectively, as follows:

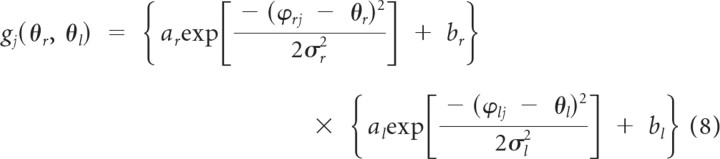and

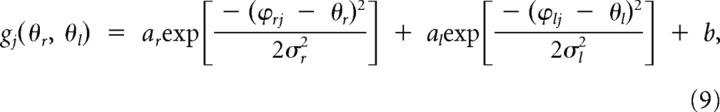where a and b are constants, and ϕ indicates the preferred direction.

Substitution of Equations 8 or 9 into Equation 5 yielded the theoretical transfer function

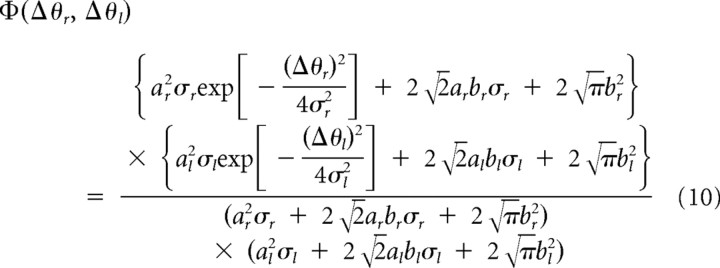for the multiplicative encoding case, and

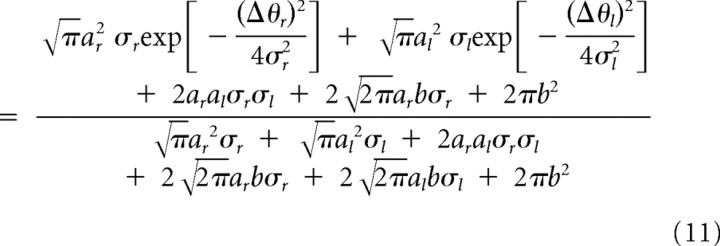for the additive encoding case.

To estimate the parameters in the primitives (Eqs. 8, 9), the data of motor learning transfer when changing the movement direction of one arm in Experiment 1 [i.e., Φ(Δθ_r, 0) and Φ(0, Δθ_l)] were fitted by a Gaussian function as follows:

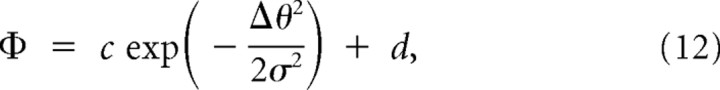using the method of least squares. Then, the parameters of the primitives (Eq. 8 or 9) were estimated by comparing the parameters of Equation 12 with Equation 10 or 11.

Estimating the parameters α and K.

The trial-dependent changes in movement error when a constant force f is imposed for only a particular movement combination (θ_r, θ_l) is as follows:

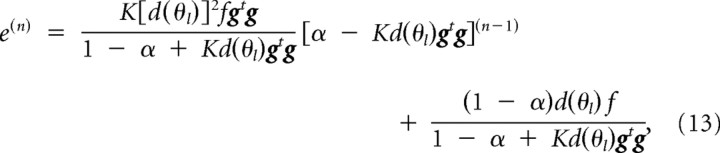where g is the abbreviation of g(θ_r, θ_l). We estimated the values of K by fitting the trial-dependent changes in the training phase with Equation 13. The value of α was set to 0.996 in advance, adopted for the slow process of motor learning (Smith et al., 2006). We ignored the contribution of the fast process because a relatively high number (500–1000) of training trials were performed in our experiments.

Simulation of state space model.

The simulations of Experiments 1, 3, 4, and 5 were performed 100 times each using Equations 1–3 with the identified primitive (i.e., Eq. 8 for the multiplicative model or Eq. 9 for the additive model). The task schedule was randomized for the 100 simulations, and the output data were averaged. The initial condition was w = 0.

Statistics: Experiments 1 and 2.

To determine the effect of the movement of the opposite arm on the aftereffects, a one-way repeated-measures ANOVA with factors of the opposite-arm movement direction (six directions) was performed for the data obtained when the trained arm was moving in the original direction. A post hoc multiple-comparison test (Tukey–Kramer) was then performed to explore differences in the aftereffect among six movement directions of the opposite arm.

To test which encoding scheme, additive or multiplicative, was more likely, we compared the actual aftereffects and the artificial aftereffects constructed based on each encoding scheme. More specifically, to construct the artificial data of the generalization curve f(θ_r, θ_l), the aftereffects obtained when only the movement direction of the trained arm was changed (eight data points [i.e., f̂(0, θ_l)]) were shifted as f̂(0, θ_l) + f̂(θ_r, 0) − f̂(0, 0) for additive encoding or multiplied as f̂(0, θ_l) f̂(θ_r, 0)/f̂(0, 0) for the multiplicative encoding model. We used 13 aftereffects [i.e., f̂(0, θ_l) and f̂(θ_r, 0)] to predict the other 35 aftereffects using both multiplicative and additive models. Then, the sums of the squared residual errors between the predicted and actual aftereffects of those 35 data points were calculated for each participant; the data of the multiplicative and additive models were subsequently compared using one-way repeated-measures ANOVA with factors of model type.

Statistical analysis: Experiments 3, 4, and 5.

To evaluate how accurately the model predicted the actual aftereffects, we performed linear regression between the aftereffects obtained experimentally (f̂_exp) and those predicted by the model (f̂_mdl) as f̂_exp = β_l + β₂f̂_mdl [the number of data was calculated as movement configurations × participants; i.e., 640 (64 × 10) for Experiment 3 and 80 (16 × 5) for Experiments 4 and 5]; the correlation coefficient (R²), intercept (β₁), and slope (β₂) were also calculated. Since the β₁ and β₂ may differ by participant, we checked the validity of the regression by performing linear regression with a linear mixed model: f̂_exp = β₁ + β₂f̂_mdl +b₁ +b₂f̂_mdl + ε, where the b₁ and b₂ are random effects (participant) of the intercept and slope, respectively. Since the inclusion of the random effects did not significantly improve the regression in Experiments 3–5 (p > 0.05 by the likelihood-ratio test), we adopted a simple linear model.

Results

Experiment 1: effect of motor learning transfer when changing the movement direction of each arm

This experiment was designed to investigate how the adaptation of the left arm to a novel force field acquired while reaching both arms forward was transferred to the same arm when the movement directions of both arms were changed (8 directions for the trained arm and 6 directions for the opposite arm, i.e., 8 × 6 = 48 combinations; Fig. 1C) and when the movement was performed unimanually (8 directions). With the training, the lateral deviation of the left handle at the peak velocity gradually decreased (Fig. 2A). After the 80 training trials, we performed catch trials at every other trial. The lateral movement deviation of trials immediately following the catch trials was not significantly different from those of the last 10 trials of the training phase (p = 0.5633 by t test; Fig. 2A). This indicated that catch trials using the error-clamped method did not deteriorate the motor learning performance, and confirmed the validity of conducting the catch trials so frequently. The adaptation of the trained hand did not seem to influence the untrained hand. There was no significant lateral deviation throughout the experiment (Fig. 2B; t test with Bonferroni's correction for 4 bins of 20 trials), which is consistent with the results of recent studies showing that there is no influence of the perturbation to one arm on another hand when two cursors are appropriately presented for both arms (Diedrichsen, 2007; Kasuga and Nozaki, 2011).

Figure 2.

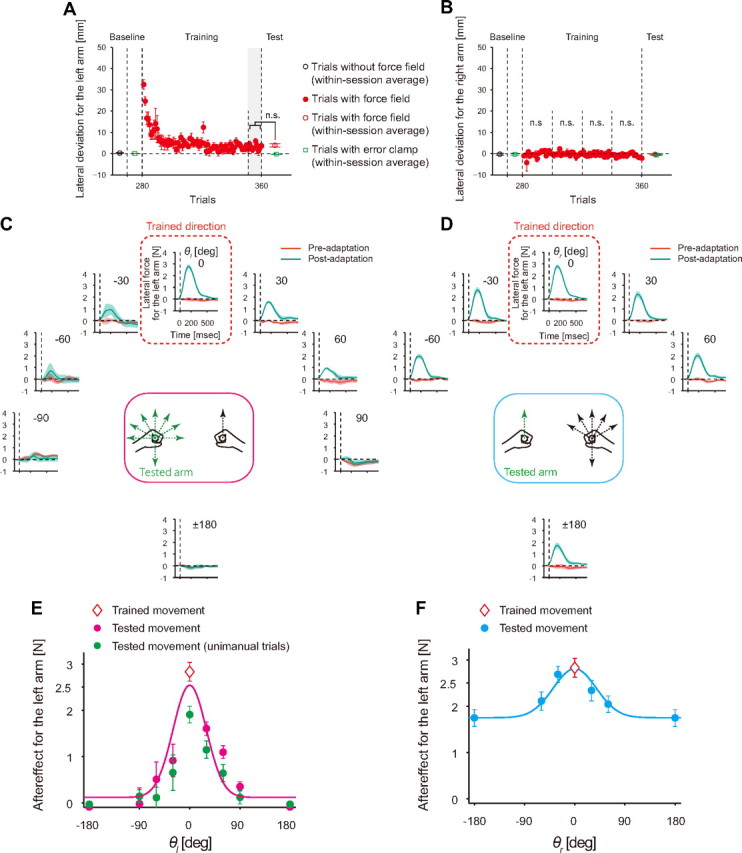
Generalization pattern of motor learning of the left arm with the movement direction of each arm (Experiment 1). A, B, Learning curves for the trained left arm (A) and untrained right arm (B). The data from all participants were averaged (error bars indicate SE). The filled red circles indicate trial-by-trial values of lateral hand deviation at the peak movement speed. The open red and black circles indicate within-session averaged values. The open green squares indicate within-session averaged values of lateral hand deviation during the error-clamp trials. Averaged lateral deviation of the left hand across the last 10 trials during the training session (gray shaded area) and within-session averaged values during the test session (open red circle in the test session) were not significantly different (p > 0.05 by t test; A). It should be noted that no significant lateral deviation was observed for the right arm throughout the experiments (p > 0.05 by t test with Bonferroni's correction; B). C, D, Each peripheral plot displays the time-dependent profile of lateral force exerted by the trained left arm during the error-clamp trials before (preadaptation; red) and after (postadaptation; green) the training session. The data were averaged over all participants, and the shaded areas indicate the SE. The location of each plot corresponds to the movement direction of the left (C) and right (D) arms, as illustrated by the center panel. E, F, Generalization patterns when the movement direction of the left (E) and right (F) arms was changed while the movement direction of the other arm was fixed (mean ± SE). Each point indicates the aftereffect of the trained left arm. The open diamond at the center indicates the data for the trained movement. The solid line is a Gaussian function fitted to the data.

First, we demonstrated how the movement direction of each arm influenced motor learning transfer. Figure 2 indicates the aftereffects when the movement direction of the trained arm (Fig. 2C) or the opposite arm (Fig. 2D) was changed while maintaining the movement direction of the other arm in the original trained direction. When the movement direction of the trained arm was altered, the aftereffect gradually decreased as the movement direction deviated more from the original direction, converging monotonically to 0 when the angular difference was greater than 90° (Fig. 2C,E). Figure 2E also shows the generalization pattern observed in the unimanual movement. The amplitude of the generalization function decreased during the unimanual movement, demonstrating the partial motor learning transfer from bimanual to unimanual movement, which we reported in our previous studies (Nozaki et al., 2006; Nozaki and Scott, 2009). In contrast to previous studies (Donchin et al., 2003), a bimodal generalization pattern was not observed; the aftereffects for an angular difference of 180° were not significantly different from those of 90°.

A similar decay pattern in the aftereffect was observed when the movement direction of the opposite arm was changed (Fig. 2D,F). However, unlike the pattern for the trained arm (Fig. 2C,E), the aftereffects decayed to 61.7 ± 16.5% (mean ± SD) of the aftereffect of the original direction (Fig. 2F). The movement directions of the opposite (right) arm significantly affected the aftereffect (F_(5,35) = 16.3; p < 0.001 by one-way repeated-measures ANOVA), and a post hoc test revealed significant differences for several movement directions [0° vs (30°, ±60°, or ±180°), 30° vs ±180°, and −30° vs (±60° or ±180°)], indicating that the aftereffect was a smooth function of the movement direction of the opposite arm and that the movement direction of the opposite arm smoothly interferes with the internal model.

The generalization pattern is considered to reflect the possible encoding pattern of the kinematics in the primitives of the internal model (Thoroughman and Shadmehr, 2000; Donchin et al., 2003; Hwang et al., 2003; Poggio and Bizzi, 2004; Sing et al., 2009). The generalization pattern observed when changing the opposite-arm movement direction suggests that the primitives also encode neuronal information that changes smoothly with the kinematics of the opposite arm.

The generalization curves (Fig. 2E,F) were fitted well by the Gaussian function (Eq. 12): The variance explained by this model was high [R² = 0.85 and 0.94 for Φ(0, Δθ_l) and Φ(Δθ_r, 0), respectively]. From the estimated parameters (c, d, and σ) summarized in Table 2, we calculated the concrete encoding function for the multiplicative and additive encoding models (Eqs. 8, 9) (Fig. 3A,B). The parameters are also shown in Table 2.

Table 2.

Parameter estimates of generalization functions and primitives

	c	d	σ (°)	R2
Φ(0, Δθl)	0.955	0.045	29.9	0.849
Φ(Δθr, 0)	0.377	0.623	38.5	0.940

Multiplicative	ar	br	σr (°)	al	bl	σl (°)
	1.00	0.318	27.2	1.00	0.0158	21.1

Additive	ar	σr (°)	al	σl (°)	b
	0.553	27.2	1.00	21.1	−0.252

Common	N	α	K	d(θl)
	100	0.996	0.00724	10 (θl = 0, 180)
				5 (θl = 90, 270)

Experiment 1 and 2: whole generalization pattern

We trained the identified multiplicative and additive models with the task of Experiment 1. Both models exhibited almost identical generalization patterns in Φ(Δθ_r, 0) and Φ(0, Δθ_l) but predicted completely different patterns of generalization when the movement directions of both arms were simultaneously changed (Fig. 3C,D). As expected from Equations 6 and 7, the multiplicative encoding model predicted the change of the amplitude of the generalization curves, and the additive model predicted the upward or downward shift of the curves (Fig. 3C,D).

Although the additive model predicted negative learning transfer when the movement configurations were more different from the training configuration, this was not indicated in the actual data (Fig. 4A). In contrast, the actual data appear to support the prediction made using the multiplicative model (Fig. 4A). To statistically test which model explained the actual data more accurately, we predicted the aftereffect data of 35 movement configurations from those of 13 movement configurations using both multiplicative (Eq. 8) or additive (Eq. 9) models. The residual sums of squares between the actual and predicted aftereffects of both models were then statistically compared by one-way repeated-measures ANOVA. We found a significant main effect of model (F_(1,7) = 21.96; p < 0.005) for Experiment 1. In Experiment 2 in which the right arm was trained, we also found a significant main effect of model (F_(1,7) = 9.03; p < 0.05; Fig. 4B), suggesting that the multiplicative model explains the data more accurately than the additive model.

Figure 4.

Gain modulation of the generalization pattern. The whole structure of the generalization pattern for the trained left (A) and right (B) arms when reaching each arm in different directions after the training at θ_r = θ_l = 0. Bottom left, Contour plot of the generalization pattern averaged across all participants. The color bar indicates the magnitude of the lateral force at the peak movement velocity. The white dots indicate the movement configurations at which the aftereffects were measured. Top left, Generalization curve (aftereffect vs the movement direction of the trained arm). Bottom right, Generalization curve (aftereffect vs the movement direction of the opposite arm). Each point represents the aftereffect averaged across all participants (error bar indicates SE).

Experiment 3: generalization of motor learning performed in multiple movement configurations

In Experiments 1 and 2 in which only one movement configuration was used for the learning of a force field, the generalization patterns to the other movement configurations were not localized around the movement configuration for the training, but were elongated along the axis of the movement direction of the opposite arm (Fig. 4). With this generalization pattern, when participants tried to learn different force fields simultaneously with different movement configurations, the training effects obtained with training movement configurations should influence each other and create a particular generalization pattern. Experiment 3 aimed to examine this issue and determine how accurately our multiplicative encoding model identified above in Experiment 1 (Table 2) could predict the global motor learning pattern.

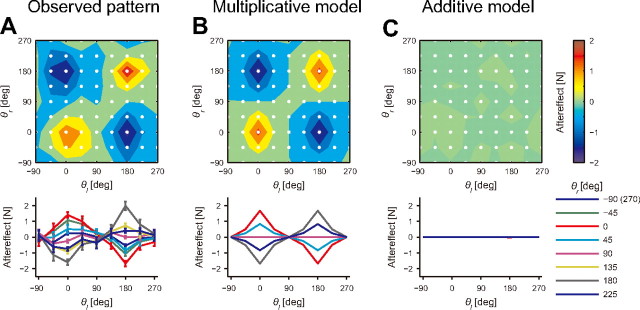
Figure 5A shows the generalization pattern measured for 64 different combinations of movement directions (8 directions for each arm) when the training was performed at movement configurations of (0, 0), (0, 180), (180, 0), and (180, 180). The participants exhibited significant aftereffects at these four points (p < 0.001 by t test with Bonferroni's correction), and the training effect gradually decayed around the training configurations This pattern was quite similar to that predicted by the multiplicative model (Fig. 5B). Linear regression between the predicted and actual aftereffects produced an R² value of 0.38 (p < 0.001); in addition, the intercept and slope of the regression line were close to 0 (−0.01 ± 0.03) and 1 (1.03 ± 0.05), respectively (mean ± SD). These results suggest that without altering the parameters of the multiplicative model identified in Experiment 1, the model accurately predicted not only the generalization pattern but also the size of the actual aftereffects even when the training was simultaneously performed at multiple movement configurations. In contrast, due to the nonlinear dependence of the force direction on the movement direction, the additive model could not adapt to this force field at all (Fig. 5C), which sharply contrasts from the patterns of the aftereffects exhibited by the participants.

Figure 5.

Generalization pattern when training was performed at multiple movement configurations. A, Contour plot of the aftereffects in Experiment 3 (top panel). The training was performed at four movement configurations [(θ_l, θ_r) = (0, 0), (0, 180), (180, 0), (180, 180)], and the aftereffects were measured at 64 movement configurations (8 movement directions for each arm) represented by the white dots. The bottom panel indicates the relationship between the aftereffects and movement direction of the trained left arm for each movement direction of the untrained right arm (mean ± SE). B, C, The generalization pattern predicted by the multiplicative (B) and additive models (C).

Experiments 4 and 5: construction of arbitrary force output by the internal model

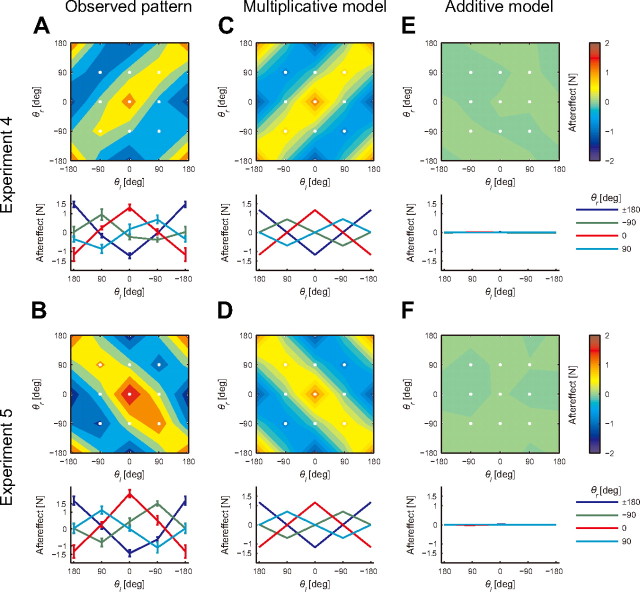
Experiments 4 and 5 were designed to investigate whether the participants could actually adapt their arm movements to a much more complicated force field that depended on the movement directions of both arms in a nonlinear fashion. The multiplicative model, whose predictions were already demonstrated to be very accurate, should enable the participants to learn such complicated force fields. As expected, the observed pattern of the aftereffects measured after a sufficient amount of training was similar to that with imposed force fields (Fig. 6A,B). These patterns were similar to those predicted by the multiplicative encoding model whose parameters were identified in Experiment 1 (Fig. 6C,D). The same linear regression analysis as the one used in Experiment 3 showed that the R² values between the predicted and actual aftereffects were significant (p < 0.001) for Experiment 4 (0.72) and Experiment 5 (0.76). In addition, the intercept and slope of the regression line of Experiments 4 and 5 were close to 0 and 1 (0.02 ± 0.05 and 1.08 ± 0.08 for Experiment 4; 0.17 ± 0.06 and 1.45 ± 0.09 for Experiment 5; mean ± SD). The slope was significantly greater than 1 in Experiment 5 (p < 0.05), while it was not significantly different from 1 in Experiment 4 (p > 0.05). Thus, although the actual aftereffects tended to be greater than the predicted aftereffects in Experiment 5, the multiplicative model was able to predict the size of the aftereffects without adjusting the parameters. In contrast, the additive model could not learn the force fields due to the nonlinear dependence on the movement directions (Fig. 6E,F). These results indicate great flexibility in constructing internal models through the linear combination of primitives that multiplicatively encode the movement directions of both arms.

Figure 6.

Simultaneous adaptation to complicated force fields. A, B, The top panel shows the contour plot of the aftereffects for the trained left arm for Experiments 4 (A) and 5 (B). The white dots represent the training and tested movement configurations (4 movement directions for each arm). The bottom panel shows the relationship between the aftereffects and movement direction of the trained left arm for each movement direction of the untrained right arm (mean ± SE). C–F, The aftereffects predicted by the multiplicative (C, D) and additive models (E, F).

Discussion

Performing flexible bimanual movement requires the internal model for each arm to predictively compensate for mechanical interactions resulting from the movement of both arms. Thus, the internal model must integrate the kinematics information from the opposite arm in addition to the relevant arm. By examining the adaptation of reaching movements to novel force fields, we demonstrated that an internal model for each arm multiplicatively encodes the movement directions of both arms and that such multiplicative encoding provides us with a flexible ability to compensate for the mechanical interaction between arms.

Encoding of opposite-arm kinematics in the primitives

As demonstrated by previous studies using a bimanual task in which the position of one arm is maintained during a disturbance resulting from the movement of the opposite arm (Viallet et al., 1992; Bays and Wolpert, 2006; Johansson et al., 2006; Jackson and Miall, 2008), the brain can predictively compensate for mechanical disturbance by using information about the movement of the opposite arm. Recent studies suggest that the brain displays such an ability even during reaching movements. Two distinct internal models for an arm movement can be constructed depending on whether the other arm is moving or stationary (Nozaki et al., 2006), and whether the other arm is moving in the same or opposite (or orthogonal) direction (Howard et al., 2010). Although it is highly difficult to evaluate the details of the encoding scheme from only these results, the data suggest the possibility that the primitives of the internal models do encode the kinematics of the opposite arm.

Previous neurophysiological findings on the role of neurons in motor areas for motor learning also imply that the encoding of opposite-arm kinematics is very likely. Many neurons in the contralateral primary motor cortex (MI) are load sensitive (Evarts, 1968; Kalaska et al., 1989), and this load sensitivity emerges during motor learning (Gandolfo et al., 2000; Li et al., 2001; Arce et al., 2010). The neurons of the supplementary motor area (Padoa-Schioppa et al., 2002, 2004) and the premotor area (Xiao et al., 2006) of the contralateral hemisphere are also involved in the adaptation to novel loads. Thus, the adaptation to a novel force field can be viewed as the development of a load representation in a population of neurons in these areas.

Interestingly, movement of the ipsilateral arm also modifies the activity of neurons in these motor areas (Donchin et al., 1998; Cisek et al., 2003; Ganguly et al., 2009). Therefore, when the left arm is adapted to a force field while the right arm is being moved in a particular direction, the representation of the force field is constructed specifically for the right-arm movement direction. As such, when the movement direction of the right arm changes from this original direction, the neuronal influence of the right arm also changes, which should result in the degradation of left-arm motor learning. Furthermore, considering that the influence on the MI neuron response smoothly changes with ipsilateral arm movement direction during bimanual movement (Rokni et al., 2003), the degree of the interfering effects is also likely to change smoothly with movement direction.

Consistent with these speculations, we found that the influence of the opposite-arm movement direction on motor learning (i.e., aftereffects) smoothly changed with direction (Fig. 2F). This indicates that the primitive encodes neuronal information that changes smoothly with the movement of the opposite arm. It also provides strong evidence against the view that the formation of distinct motor memories according to the kinematics of the opposite arm (Nozaki et al., 2006; Howard et al., 2010) can be explained by regarding the kinematics as cognitive cues (Osu et al., 2004; Cothros et al., 2009); such a scheme would result in abrupt, not smooth, changes in the aftereffect.

Gain field encoding in the primitives

Our next hypothesis was that the primitives integrate the movement directions of both arms multiplicatively rather than additively. Multiplicative neuronal integration, known as gain fields, was first reported for neurons in posterior parietal cortex (LIP and 7a) (Andersen and Mountcastle, 1983; Andersen et al., 1985) and later found in many other areas in the brain, including subcortical structures (Lal and Friedlander, 1990; Van Opstal et al., 1995; Boussaoud et al., 1998; Wang et al., 2010). It has been theorized that such gain field encoding is beneficial for sensorimotor transformation from multiple neuronal inputs (Pouget and Sejnowski, 1997; Salinas and Sejnowski, 2001). More specifically, neurons with gain field encoding work as a set of basis functions enabling downstream neurons to construct arbitrary outputs by flexibly and linearly combining them (Pouget and Sejnowski, 1997).

Similar to the above problem of creating a sensorimotor transformation mapping, the construction of internal models for arm movement can be regarded as a process of creating an arbitrary map from desired sensory states to a motor command for the relevant arm by flexibly combining primitives. Thus, if the gain field encoding is equipped with the primitives, this property would give the brain great flexibility in constructing an arbitrary force output from the desired state of both arms to a motor command for each arm.

We tested these multiplicative and additive encoding schemes in the primitives by investigating the generalization function of motor learning (Hwang et al., 2003; Wainscott et al., 2005). Multiplicative or additive encoding predicts multiplicative or additive generalization functions, respectively (Eqs. 8, 9). Our results clearly indicate that multiplicative encoding is more likely (Figs. 3, 4), which is consistent with our speculation based on previous theoretical work.

The strength of multiplicative encoding was exemplified by Experiments 4 and 5, in which participants adapted their left-arm movements to force fields that nonlinearly depended on the movement directions of both arms (Fig. 6). We used two different force fields with magnitudes that depended on the directional difference between the arms in either an extrinsic or intrinsic workspace (Fig. 1E,F). Due to the nonlinear dependence of the force fields on the movement directions of both arms, the additive encoding model cannot adapt to them (Fig. 6E,F), indicating that the motor learning system of bimanual movement is unlikely to place special emphasis on bimanual movement patterns, such as mirror-symmetric, parallel movements. Rather, any meaningful association between the force field and the movement patterns of both arms (Ahmed et al., 2008) may arise as a consequence of the greater flexibility in motor learning offered by multiplicative encoding of primitives.

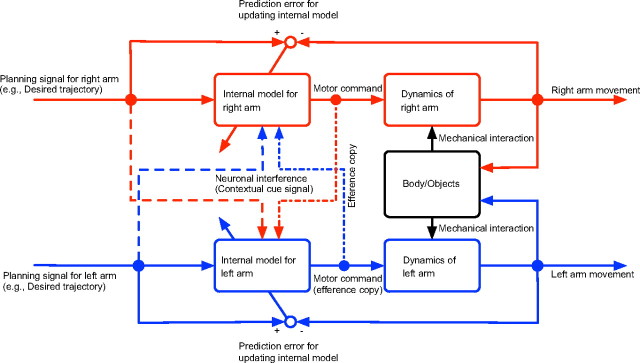
Possible scheme of bimanual movement control

On the basis of the present results, we can speculate about a possible scheme of bimanual movement control that compensates for the mechanical interaction between both arms (Fig. 7). This scheme assumes that the information regarding the desired movement of the opposite arm, the efference copy from the movement controller of the opposite arm, or both multiplicatively influences the internal model of each arm. The assumption that the contribution of sensory input is negligible can be justified by the results of a recent study demonstrating that distinct internal models cannot be established when the opposite arm is passively moved (Howard et al., 2010). We also assume that the contribution of the efference copy is relatively weak, because the trajectory of the right arm was not affected by the adaptation of the left arm (Fig. 2B). The adaptation to the force field should change the efference copy, which should influence the controller of the opposite arm.

Figure 7.

A possible feedforward control scheme for the flexible bimanual movement deduced from our experimental results. In bimanual movement, the internal model for each arm must compensate for the mechanical interactions resulting from movements of the other arm. Neuronal signals reflecting planned movements (broken lines) and/or efference copy of the other arm (dashed-dotted lines) may be multiplicatively integrated within the internal model of each arm. This multiplicative integration in the primitives contributes to construct a flexible output from each controller depending on the kinematics of both arms.

It is well known that bimanual neuronal interactions exist when bimanual actions are performed (Swinnen, 2002; Rokni et al., 2003; Swinnen and Wenderoth, 2004; Carson, 2005). However, the functional role of such neuronal interactions remains unclear. In fact, such interactions are often considered to be a source of bimanual interference that needs to be overcome (Swinnen, 2002). The results of the current study provide a novel interpretation of how these neuronal interactions may play a crucial role in the flexible control of bimanual movements (Fig. 7). Without such multiplicative interfering effects, the neural control process for the movement of an arm is unable to take movement of the other arm into account to compensate for the mechanical interaction between the movements of both arms. The present study provides, to our knowledge, the first behavioral example that gain field encoding is essential for flexible bimanual movement control and provides a possible clue to how the brain orchestrates the movements of multiple body parts into a single unified action.

Notes

Supplemental material for this article is available at http://www.p.u-tokyo.ac.jp/∼nozaki/online_materials/yokoi_gf_suppl.pdf. The supplemental material provides a detailed derivation of theoretical equations. This material has not been peer reviewed.