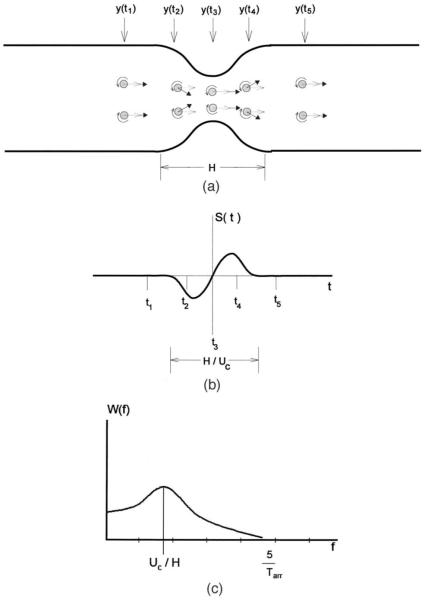
FIG. 4.
Aeroacoustic source behavior due to convection of single vortex ring through a constriction in an infinite pipe. Airflow is from left to right, vortex ring diameter is Rʋ, vortex core diameter is δʋ, and the axial length of the constriction is H. (a) Location y(t) of vortex ring, shown in cross section, at five instants t1, t2, t3, t4, and t5 during vortex passage. Orientation of vectors ω, v, and U* are shown, ω in terms of its rotation sense in the plane of the page, v by lined arrowheads, and U* by solid arrowheads. Equation (2) states that the aerodynamic force on the constriction will be maximum when v is perpendicular to U*, and zero when they are parallel. (b) Waveform of aeroacoustic source strength due to vortex ring passage through constriction, with times indicated corresponding to vortex ring positions in Fig. 4(a). Duration of source is the time H/Uc that the vortex ring takes to convect through the constriction. Note that S(t)=0 when t=t1, t3 and t5, because v and U* are parallel. The aerodynamic force changes sign as the vortex passes through the maximum constriction. (c) Spectrum of sound pressure due to the passage of a single vortex ring through the constriction. Peak occurs at Uc/H, the reciprocal of the time the source is “on.” Peak width is related to temporal extent of source signal, and becomes broader as Uc/H becomes smaller.