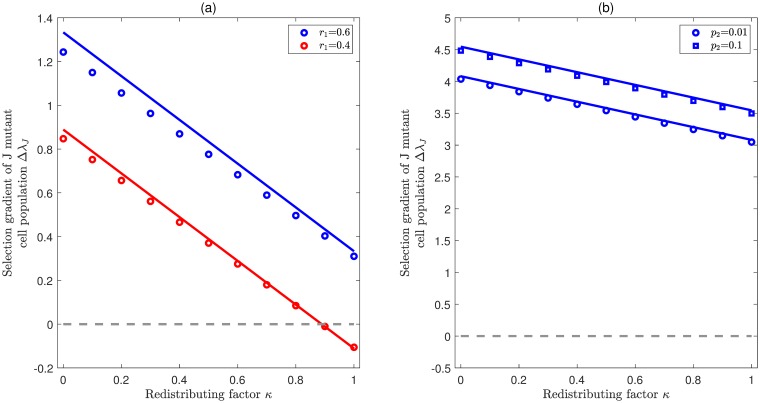
Fig 6. Selection for jumpwise de-differentiation when the effective rate of self renewal is highest in compartment 3.

Illustration of the selection gradient Δλ_J as a function of the redistributing factor κ provided that λ₀ = r₃(p₃ − q₃). In both panels, colored lines represent eigenvalue perturbation results in Eq (9) and symbols represent exact numerical solutions. The common parameters are n = 4, ρ = 0.01, d = 0.05. (a) Expanding case (λ₀ > 0). In this case, there are two different scenarios: For $r_1>\frac{r_3(2p_3-1)}{2(1-p_1){\Gamma }_{2,3,2}+(2p_1-1)}\approx 0.45$, Δλ_J is always positive (blue color). For r₁ < 0.45, Δλ_S is changed from positive to negative with the increase of κ (red color). Here p₁ = 0.5, p₂ = 0.65, p₃ = 0.85, r₂ = 0.4, r₃ = 0.6. (b) Homeostasis case (λ₀ = 0). In this case, Δλ_J is always positive. Here p₁ = 0.01, p₃ = 0.5, r₁ = 0.8, r₂ = 0.7, and r₃ = 0.2.