Bias Induced by Ignoring Double Truncation Inherent in Autopsy-Confirmed Survival Studies of Neurodegenerative Diseases

Abstract

Neurodegenerative diseases require an autopsy for confirmation of diagnosis. When death is the event of interest, studies based on autopsy-confirmed diagnoses result in right truncated survival times, since individuals who live past the end of study date do not receive a pathological diagnosis and are therefore not included in the sample. Furthermore, many studies of neurodegenerative diseases recruit subjects only after the onset of the disease, which may result in left truncated survival times. Therefore double truncation, the simultaneous presence of left and right truncation, is inherent in many autopsy-confirmed survival studies of neurodegenerative diseases. The main focus of this paper is to inform about the inherent double truncation in these studies and demonstrate how to properly estimate and compare survival distribution functions in this setting. We do so by conducting a case study of subjects with autopsy-confirmed Alzheimer’s disease and frontotemporal lobar degeneration. This case study is supported by extensive simulation studies, which provide several new contributions to the literature on survival distribution estimation in the context of double truncation.

1. Introduction

Neurodegenerative diseases, such as Alzheimer’s disease (AD) and frontotemporal lobar degeneration (FTLD), require an autopsy for a definitive diagnosis.¹ Without an autopsy-confirmed diagnosis, it is uncertain which disease a given individual may have. Hence this individual cannot be included in an autopsy-confirmed study sample pertaining to a particular disease. Therefore when the event of interest is death, studies which include only autopsy-confirmed subjects result in pure right truncation, since individuals who have the disease of interest and live past the end of study date do not receive a pathological diagnosis. Because these individuals cannot be included in the autopsy-confirmed study sample, they are treated as unobserved. Furthermore, studies that recruit individuals after the onset of the disease has occurred may result in left truncation, since individuals who succumb to the disease before they enter the study are unobserved. This simultaneous presence of left and right truncation, also known as double truncation, is therefore inherent in autopsy-confirmed studies of neurodegenerative disease.

Double truncation occurs in these studies as follows: Subjects are only observed if their time of death, t_death, occurs after the time of study entry, t_entry, and before the study end time, t_end. In other words, only subjects with t_entry ≤ t_death ≤ t_end are observed. The survival time T in individuals with neurodegenerative diseases is typically measured as the time from disease symptom onset to death. That is, T = t_death − t_onset, where t_onset is defined as the time in which disease symptom onset occurs. We therefore define the left truncation time, L = t_entry − t_onset, as the time from disease symptom onset to study entry, and the right truncation time, R = t_end − t_onset, as the time from disease symptom onset to study end. The truncation scheme t_entry ≤ t_death ≤ t_end is therefore equivalent to L ≤ T ≤ R. This truncation scheme is illustrated in Figure 1.

Figure 1.

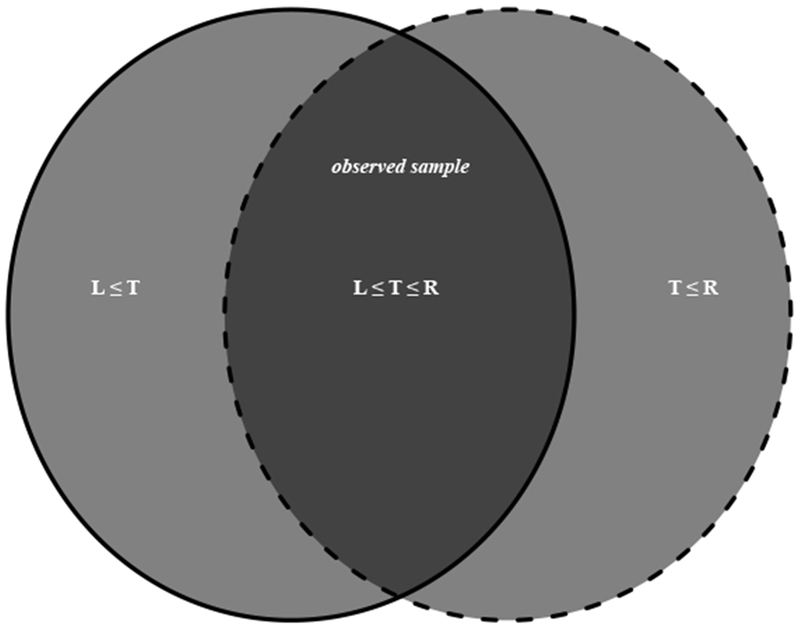
Schematic depiction of doubly truncated neurodegenerative disease data: Here L, T, and R denote the time from disease symptom onset to study entry, death, and the end of study, respectively. The solid circle (left) consists of all subjects who entered the study and are therefore not left truncated. The light grey region of the solid circle is right truncated, and consists of all subjects who entered but lived past the end of the study, i.e. {L ≤ T} ∩ {T > R}. The dotted circle (right) consists of all subjects who had an autopsy performed by the end of the study and are therefore not right truncated. The light grey region of the dotted circle is left truncated, and consists of all subjects who never entered the study but died before the end of study date, i.e. {T < L} ∩ {T ≤ R}. The observed sample is represented by the intersection of the two circles (dark grey region), and consists of all subjects who entered the study and had an autopsy performed {L ≤ T ≤ R}.

Unlike a censored individual who provides partial information about their survival time, a truncated individual is completely unobserved and provides no information to the investigator, resulting in a biased sampling scheme. Right truncation in this setting yields an observed sample that is biased towards smaller survival times, since individuals with longer survival times are more likely to live past the end of the study. The left truncation simultaneously leads to an observed sample that is biased towards larger survival times, since individuals with shorter survival times are more likely to succumb to the disease before they enter the study. Therefore any estimation procedure of the survival time distribution which does not account for the double truncation will be biased. In this paper, we focus on autopsy-confirmed studies of neurodegenerative diseases, but note that double truncation can be present in other studies.²

The bias introduced in autopsy-confirmed survival studies is briefly discussed in the context of Cox regression models.³ One of the goals of our paper is to further emphasize and explore this important issue by examining the bias introduced in autopsy-confirmed survival studies in the context of survival distribution estimation, thus avoiding any assumptions about the survival time. Survival distribution estimation is useful in time to event analysis as it serves as the first step of evaluating the disease risk. It is a useful exploratory tool before any regression modeling. It is particularly suited for graphical display which is an essential part of disease risk modeling.

There are a few papers devoted to the estimation of the survival time distribution in the presence of double truncation. Bilker and Wang² were one of the first to motivate the problem of double truncation by noticing that it was present in certain retrospective studies of survival from HIV infection to AIDS. Motivated by doubly truncated quasar data, Efron and Petrosian⁴ introduced a nonparametric maximum likelihood estimator (NPMLE) of the survival time distribution under double truncation. Shen⁵ established the asymptotic properties of the NPMLE, and introduced a nonparametric estimator of the truncation distribution. Under the assumption that the joint distribution function of the truncation times comes from a parametric family, Shen⁶ and Moreira and de Ũna-Álvarez⁷ introduced a semiparametric maximum likelihood estimator (SPMLE) for the survival time distribution function under double truncation. The NPMLE and SPMLE both assume independence between survival and truncation times. A version of a conditional Kendall’s Tau was introduced by Martin and Betensky⁸ to test for dependence between survival and both left and right truncation times.

Despite the wide use of autopsy-confirmed studies of neurodegenerative diseases, practitioners continue to ignore the inherent selection bias due to double truncation. This may be due to either a lack of awareness of the problem or of existing methods to handle it. Our main objective is to inform the reader about the inherent double truncation in these studies and highlight the importance of accounting for it. We do so by conducting a case study of two neurodegenerative diseases, where we show how to properly estimate and compare the survival distributions in the presence of double truncation. This case study is supported by extensive simulation studies. Specifically, our simulation studies include an in-depth comparison of the SPMLE, NPMLE, and the naïve empirical distribution function under a wide variety of double truncation schemes. These truncation schemes include cases when the assumptions of the SPMLE and NPMLE are violated. Through these simulation studies, we discover that the SPMLE and NPMLE are sensitive to the assumption of independence between the survival times and truncation times. We also discover that the SPMLE is robust to model misspecification when a gamma distribution with two unknown parameters is assumed for the truncation times. This discovery provides different insights in contrast to previous literature, which has concluded that the SPMLE can be heavily biased under misspecification of the truncation distribution.^6,7

The outline of this paper is as follows. In Section 1.1, we briefly introduce the data example for autopsy-confirmed studies of neurodegenerative diseases. In Section 2, we introduce notation and the SPMLE and NPMLE of the survival distribution function, as well as formal tests to compare distribution functions in the presence of double truncation. The simulations to evaluate and compare the performance of these estimators are presented in Section 3. In Section 4 we conduct a case study in which we estimate and compare the survival curves for subjects with an autopsy-confirmed diagnosis of AD or FTLD. Concluding remarks and limitations of these methods are discussed in Section 5. Additional results and code are provided in the online supplementary materials.

1.1. Case Study: Autopsy-confirmed studies of neurodegenerative diseases

In our case study in Section 4, we focus on autopsy-confirmed AD and FTLD. While both neurodegenerative diseases lead to dementia and loss of the basic activities of daily living, their underlying disease pathologies differ. The pathology of AD is characterized by accumulations of neurofibrillary tangles and senile plaques in the brain. AD is the leading cause of dementia, and symptoms typically become present in later ages. Frontotemporal degeneration (FTD) is a common form of young-onset dementia and is typically caused by a spectrum of pathologies known as FTLD,⁹ which are different than the pathologies underlying AD.

The study and comparisons of survival times of patients with neurodegenerative diseases are important for planning the resources needed to care for patients during a period of decreased ability, allocating public resources for disease prevention and care, giving insight towards developing disease modifying therapies, and predicting the future prevalence of the disease. Previous studies of subjects with autopsy-confirmed FTLD have concluded that survival from symptom onset ranges from 6 years to 10.5 years.^10–12 Studies based on clinical diagnoses of FTLD have concluded that survival from symptom onset ranges from 7 to 13 years, and that this range is comparable to that in AD.¹³ However the studies which consisted of autopsy-confirmed subjects did not adjust for double truncation, and were therefore subject to selection bias. The remaining studies consisted of clinically diagnosed subjects. Clinical diagnoses are not always accurate in diagnosing a particular neurodegenerative disease,¹⁴ and therefore the conclusions of these studies may not be accurate.

In our data example, we aim to study and compare autopsy-confirmed samples using methods which account for double truncation, thereby eliminating the issues described in the previous studies above. Our observed sample contains all subjects who entered the neurodegenerative disease autopsy program at the University of Pennsylvania after 1995, and had an autopsy-confirmed diagnosis of AD (n=47) or FTLD (n=31) before 2012. Here we let t_onset denote the time of AD or FTLD symptom onset. The survival time T is the time from t_onset to death. The left truncation time L is the time from t_onset to the time at which the subject first entered the program. The right truncation time R is the time from t_onset to July 1,2012.

In addition to estimating the survival curves for each group, we aim to formally compare the survival probabilities at different time points. These analyses are performed in our case study in Section 4. The methods used in these analyses are supported by the simulation studies conducted in Section 3.

2. Existing methods to adjust for double truncation

We state the problem in statistical terms as follows. Let T denote the survival time of interest (e.g. survival time from disease symptom onset), L denote the left truncation time (e.g. time from disease symptom onset to entry into the study), and R denote the right truncation time (e.g. time from disease symptom onset to the end of study date). Let N denote the size of the target sample - the sample that would have been observed had there been no truncation present in the study. We denote the observed data as (T_j, L_i, R_i) for i = 1,…, n. Due to double truncation, we only observe (T_i, L_i, R_j) for n ≤ N individuals who live long enough to enter the study (i.e. T ≥ L) and do not live past the end of the study (i.e. T ≥ R). Here we have denoted the population random variables from the target population without subscripts, and the sampling random variables from the observed sample with subscripts.

We are interested in estimating the cumulative distribution function F of T, where F(t) = P(T ≤ t) for a given time t. The survival distribution function is given by S(t) = 1 − F(t). We note that right censoring is not present in autopsy-confirmed studies of neurodegenerative diseases. This is because individuals who live past the end of the study are undiagnosed (since an autopsy is never performed) and not included in the study sample. Therefore no information is available on the survival time of these individuals. With no censoring, the standard estimator of the cumulative distribution function of the survival times is just the empirical cumulative distribution function (eCDF) ${\widehat{F}}_{\mathit{emp}}(t)=\frac{1}{n}{\Sigma }_{i=1}^n{I}_{[T_i\le t]}$ for a given time t, where I is the indicator function. We show through simulations in the next section that this estimator, which does not take into account that the data are doubly truncated, is biased. Throughout the paper, we refer to the eCDF as the naïve estimator and denote it by ${\widehat{F}}_{\mathit{emp}}$. We note that the eCDF is equivalent to the Kaplan-Meier estimator when neither censoring nor truncation is present.

The methods to estimate F, described below, assume that the survival times are independent of the left and right truncation times. That is, (L, R) is independent of T. It is also assumed that no censoring is present, and that (L_i, T_i, R_i) are independent and identically distributed for i = 1,…, n. For any cumulative distribution function Q, we define the left endpoint of its support by a_Q = in f{x : Q(x) > 0} and the right endpoint of its support by b_Q = in f{x : Q(x) = 1}. Let K denote the joint cumulative distribution function of the left and right truncation times. Let H_L(l) = K(l, ∞) and H_R(r) = K(∞, r) denote the marginal cumulative distribution functions of L and R, respectively. The methods described below assume that a_HL < a_F ≤ a_HR and b_HL ≤ b_F < b_HR. These conditions are needed for identifiability of the cumulative distribution function estimators.¹⁵

The two existing methods for estimating the cumulative distribution function under double truncation are the SPMLE and the NPMLE. Both make no assumptions about the distribution of the survival times, but the SPMLE assumes that the truncation times L and R have a joint cumulative distribution function, Kθ, which depends on a parameter θ. An estimate $\widehat{\theta }$ of θ can be obtained and then used to compute $W_{\widehat{\theta }}(T_i)$,^6,7 the estimated likelihood of observing a subject with survival time T_i in the sampled population relative to the target population. Specifically, $W_{\widehat{\theta }}(T_i)=P_{\widehat{\theta }}(L\le T\le R\mid T=T_i{)}^{-1}$, the inverse of the estimated probability (under parametric assumptions) of observing a subject in the study sample with survival time T = T_i.

The SPMLE is then a weighted sum of the elements I(T_i < t) of the eCDF and is given by

$${\widehat{F}}_{SP}(t)=\frac{1}{n}\sum _{i=1}^n{W}_{\widehat{\theta }}(T_i)\times I(T_i\le t).$$ (1)

Under the regularity conditions given by Shen,⁶ namely that Kθ (l, r) is continuous in (l, r) for each θ in a compact set ϴ, and K_θ(l, r) is continuously differentiable in θ for each fixed (l, r), we have that $\sqrt{n}({\widehat{F}}_{SP}(t)-F(t))\to N(0,{\sigma }^2(t))$. A consistent estimator of the asymptotic variance σ²(t), which we denote by ${\widehat{\sigma }}_{SP}^2(t)$, is provided in Moreira and de Ũna-Álvarez⁷ (Section 2, p. 1350). This result also rests on the assumption that the truncation distribution is correctly specified. The distributional assumptions for the truncation times can be checked using the test statistics introduced in Moreira et al.¹⁶

The NPMLE makes no distributional assumptions about the truncation times. Similar to the SPMLE, the NPMLE is weighted by $\widehat{W}(T_i)$, the nonparametric estimate of the likelihood of observing a subject with survival time T in the sampled population relative to the target population. Here $\widehat{W}(T_i)=\widehat{P}(L\le T\le R\mid T=T_i{)}^{-1}$, the inverse of the estimated probability (under no parametric assumptions) of observing a subject in the study sample with survival time T = T_i. The NPMLE is then given by

$${\widehat{F}}_{NP}(t)=\frac{1}{n}\underset{i=1}{\overset{n}{\Sigma }}\widehat{W}(T_i)\times I(T_i\le t).$$ (2)

Details of this estimation procedure, along with proofs for the consistency and asymptotic normality of ${\widehat{F}}_{NP}(t)$, are given in Shen.⁵ Due to the complicated nature of ${\widehat{F}}_{NP}(t)$, we apply the simple bootstrap method to obtain a variance estimator,¹⁷ which we denote by ${\widehat{\sigma }}_{NP}^2(t)$. The simple bootstrap has been shown to provide a good approximation to the variance of ${\widehat{F}}_{NP}(t)$.¹⁷

Often we would like to test whether two survival distributions are equal. Under double truncation, this can be done using the semiparametric extension of the Mann-Whitney test.² This estimator also makes use of the parametric distribution of the truncation times. Let (L_1i, T_1i, R_1i), 1 ≤ i ≤ n_i be the observed data from group 1 and (L_2j, T_2j, R_2j), 1 ≤ j ≤ n₂ be the observed data from group 2. Here it is assumed that (L₁, R₁) have a parametric joint cumulative distribution function K_θ and (L₂, R₂) have a parametric joint cumulative distribution function H_γ, which depend on the parameters θ and γ, respectively. Estimators of θ and γ, denoted by $\widehat{\theta }$ and $\widehat{\gamma }$, can be obtained using the estimation procedure for the SPMLE.^6,7 The two-sample U-statistic is of the form

$$U(\widehat{\theta },\widehat{\gamma })=\frac{1}{n_1{n}_2}\underset{i=1}{\overset{n_1}{\Sigma }}\underset{j=1}{\overset{n_2}{\Sigma }}\mathit{sign}(T_{1_i}-T_{2_j})\times W_{1\widehat{\theta }}(T_{1_i})\times W_{2\widehat{\gamma }}(T_{2_j}).$$

Similar to the definition of $W_{\widehat{\theta }}(T_i),W_{1\widehat{\theta }}(T_{1_i})$ is the inverse of the estimated probability of observing a subject from group 1 in our study sample with survival time T_1i, and $W_{2\widehat{\gamma }}(T_{2_j})$ is the inverse of the estimated probability of observing a subject from group 2 in our study sample with survival time T_2j.

Bilker and Wang’s U-statistic tests whether two survival distributions are equal across all time points.² We test whether the probability of survival between two independent groups are equal at a single time point t as follows. Let F_j (t) denote the true distribution function at time t for group j = 1,2, and let ${\widehat{F}}_1(t)$ and ${\widehat{F}}_2(t)$ be any independent estimators of F₁ (t) and F₂(t) which are consistent and asymptotically normal, with asymptotic variances ${\sigma }_1^2(t)$ and ${\sigma }_2^2(t)$, respectively. Then the statistic $W_t=\frac{[{\widehat{F}}_1(t)-{\widehat{F}}_2(t){]}^2}{{\widehat{\sigma }}_1^2(t)+{\widehat{\sigma }}_2^2(t)}$ has an asymptotic ${\chi }_1^2$ distribution¹⁸ (see Section 7.8 of reference 18 for justifications). Here ${\widehat{\sigma }}_j^2(t)$ is any consistent estimator of ${\sigma }_j^2(t)$ (e.g., ${\widehat{\sigma }}_{SP}^2$ (t)) for j = 1,2.

3. Simulation study

We conducted a simulation study to further investigate the impact of ignoring double truncation in autopsy-confirmed survival studies of neurodegenerative disease and to assess the performance of the SPMLE and NPMLE under different truncation schemes. Specifically, we compared the SPMLE (${\widehat{F}}_{SP}$) and NPMLE (${\widehat{F}}_{NP}$) to the eCDF (${\widehat{F}}_{\mathit{emp}}$) on bias ($\widehat{F}-F_0$), where F₀ is the true distribution function, observed sample standard deviations (SD), estimated standard errors ($\widehat{\mathrm{SE}}$), mean squared errors (MSE), and the average empirical coverage probability of the 95% confidence intervals (Cov). The standard errors for ${\widehat{F}}_{SP}$ and ${\widehat{F}}_{NP}$ are estimated by ${\widehat{\sigma }}_{SP}$ and ${\widehat{\sigma }}_{NP}$, respectively. We also compared the bias and observed sample standard deviation of the estimated median survival time ${\widehat{t}}_{0.5}$ across these estimators. We conducted 1000 simulation repetitions with a target sample size of n=50 and n=250. In order to get to the desired sample size n, we simulated n/p₀ observations to account for truncation, where p₀ is the true probability of observing a randomly selected subject from the target sample.

For these simulations, we generated the survival time from disease symptom onset, T, as gamma(10,1). The time from disease symptom onset to study entry, L, was generated as gamma(α₁, β₁), and the time from disease symptom onset to the end of study, R, was generated as gamma(α₂, β₂). In the following models, we changed the values of (α_i, β₁) and (α₂, β₂) to adjust the percentage of truncated observations. In model 1, we set (α₁, β₁) = (4.5,1.5) and (α₂, β₂) = (8,2.5), which resulted in moderate left truncation (22%) and mild right truncation (8%), with a total of 30% of the observations truncated. In model 2, we reduced the left truncation and increased the right truncation by setting (α₁, β₁) = (3,1) and (α₂, β₂) = (5, 2), which resulted in 55% of truncated observations (2% on the left and 53% on the right). In model 3, we set (α₁, β₁) = (5,2) and kept (α₂, β₂) = (5,2). This resulted in heavy left and right truncation and a total of 80% of the observations truncated (48% on the left and 53% on the right).

Figure 2 displays the bias of ${\widehat{F}}_{SP}$, ${\widehat{F}}_{NP}$, and ${\widehat{F}}_{\mathit{emp}}$ across the 1st through 9th deciles of F₀ for the three models. Here ${\widehat{F}}_{SP}$ has little bias regardless of sample size or truncation proportion, and ${\widehat{F}}_{NP}$ is slightly biased in the right tail of the distribution under smaller sample sizes and heavy right truncation, and has little bias otherwise. The naïve estimator, ${\widehat{F}}_{\mathit{emp}}$, is biased in all three models. The bias of ${\widehat{F}}_{\mathit{emp}}$ in model 1 is negative since the proportion of missing observations due to left truncation is slightly greater than the proportion missing due to right truncation, and thus we are under sampling the smaller survival times. In model 2, this bias is both positive and larger in magnitude relative to model 1, since we are severely under sampling the larger survival times due to the heavy right truncation. In model 3, this bias is negative across the 1st through 4th deciles of F₀, and positive across the 5th through 9th deciles of F₀. The bias here is smaller in magnitude relative to model 2, since we are (almost) equally under sampling the smaller and larger survival times, and therefore the bias due to left truncation is canceling out some of the bias due to right truncation.

Figure 2.

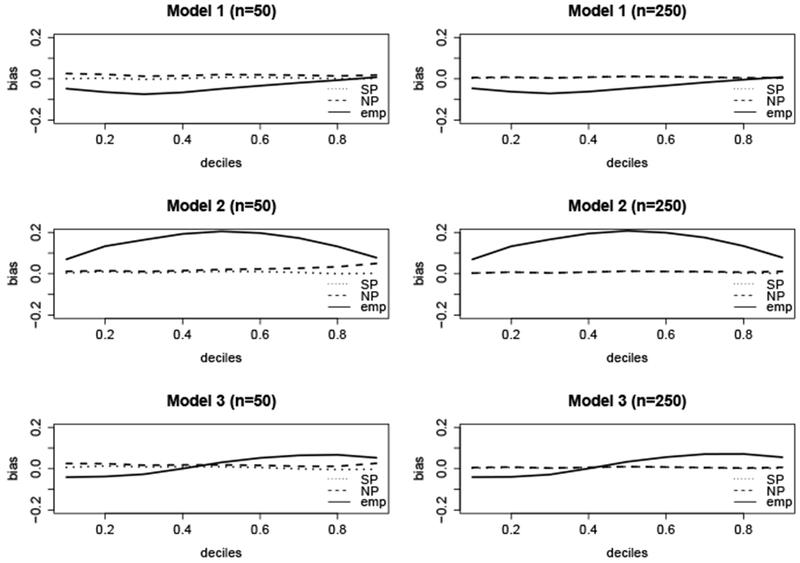
Bias of ${\widehat{F}}_{SP}$ (), ${\widehat{F}}_{NP}$ (), and ${\widehat{F}}_{\mathit{emp}}$ () at t_0.1, …,t_0.9, which are the deciles of the true survival time distribution F₀. Here F₀(t_0.1.) = 0.1, F₀(t_0.2) = 0.2, etc.

Table 1 compares (absolute) bias($\widehat{F}$), SD($\widehat{F}$), $\widehat{SE}(\widehat{F})$, MSE($\widehat{F}$), cov($\widehat{F}$), bias(${\widehat{t}}_{0.5}$), and SD(${\widehat{t}}_{0.5}$) for $\widehat{F}={\widehat{F}}_{SP}$, $\widehat{F}={\widehat{F}}_{NP}$, and $\widehat{F}={\widehat{F}}_{\mathit{emp}}$. With the exception of bias(${\widehat{t}}_{0.5}$) and SD(${\widehat{t}}_{0.5}$), these statistics were averaged across the 1st through 9th deciles of F₀. For example, bias($\widehat{F}$) in the first line of Table 1 represents the average absolute value of the bias corresponding to ${\widehat{F}}_{SP}$ in the top left panel of Figure 2. For $\widehat{F}={\widehat{F}}_{NP}$, $\widehat{SE}(\widehat{F})$ was based on 200 bootstrap resamples. The median survival time (t_0.5) of the gamma(10, 1) distribution is 9.7. From Table 1, we see that ${\widehat{F}}_{SP}$ and ${\widehat{F}}_{NP}$ greatly outperform ${\widehat{F}}_{\mathit{emp}}$ in terms of bias. Furthermore, with the exception of model 3 for n=50, ${\widehat{F}}_{\mathit{emp}}$ has a greater MSE than ${\widehat{F}}_{NP}$ and ${\widehat{F}}_{NP}$ and is therefore less efficient. When the sample size is small, ${\widehat{F}}_{SP}$ has a slightly lower MSE than ${\widehat{F}}_{NP}$. The average coverage probabilities of the 95% confidence intervals for ${\widehat{F}}_{SP}$ and ${\widehat{F}}_{NP}$ are close to the nominal level of 0.95 when the sample size is large. This is not the case for ${\widehat{F}}_{\mathit{emp}}$, where the coverage probabilities are not even close to the nominal level, even under mild truncation. The bias of the survival distribution and median survival time based on ${\widehat{F}}_{\mathit{emp}}$ were much greater in model 2, since the truncation scheme in models 1 and 3 resulted in a sampling scheme that (almost) equally under sampled the smaller and larger survival times, and therefore the bias due to left truncation canceled out a large amount of the bias due to right truncation.

Table 1.

Simulation results: Survival times simulated from a gamma(10,1) distribution. Left and right truncation times correctly assumed to come from a gamma(α₂, β₂) and gamma(α₂, β₂) distribution, respectively. Model 1 corresponds to (α₁, β₁) = (4.5, 1.5) and (α₂, β₂) = (8, 2.5). Model 2 corresponds to (α₁, β₁) = (3, 1) and (α₂, β₂) = (5, 2). Model 3 corresponds to (α₁, β₁) = (5, 2) and (α₂, β₂) = (5, 2). Here q_L, q_R, q are the proportion of observations missing due to left, right, and double (left and right) truncation, respectively, and n is the size of the observed sample. ${\widehat{F}}_{SP}$ denotes the SPMLE, ${\widehat{F}}_{NP}$ denotes the NPMLE, and ${\widehat{F}}_{\mathit{emp}}$ denotes the naïve empirical CDF which ignores double truncation. These estimators were all computed at t_0.1, …, t_0.9, the 1st through 9th deciles of the true survival distribution F₀. For a given estimator $\widehat{F}$, Bias($\widehat{F}$) is the (absolute) difference between $\widehat{F}$ and F₀, averaged across the 9 deciles. Here SD($\widehat{F}$) is standard deviation of $\widehat{F}$ across simulations, $\widehat{SE}(\widehat{F})$ is estimated standard error of $\widehat{F}$, $\mathit{MSE}(\widehat{F})$ is mean squared error of $\widehat{F}$, and Cov($\widehat{F}$) is 95% coverage, all averaged across the 9 deciles. Here ${\widehat{t}}_{0.5}$ is the estimated median value based on $\widehat{F}$. The true median value based on F₀ is t_0.5 = 9:7. Here Bias(${\widehat{t}}_{0.5}$) = ${\widehat{t}}_{0.5}$ - t_0.5 and SD(${\widehat{t}}_{0.5}$) is the standard deviation of ${\widehat{t}}_{0.5}$ across simulations.

Model	qL, qR, q	n	Estimator	Bias($\widehat{F}$)	SD($\widehat{F}$)	$\widehat{\mathrm{SE}}(\widehat{F})$	MSE($\widehat{F}$)	Cov($\widehat{F}$)	Bias(${\widehat{t}}_{0.5}$)	SD(${\widehat{t}}_{0.5}$)
			${\widehat{F}}_{SP}$	0.005	0.069	0.075	0.005	0.927	−0.028	0.622
1	0.22,0.08,0.30	50	${\widehat{F}}_{NP}$	0.021	0.070	0.069	0.005	0.910	−0.050	0.664
			${\widehat{F}}_{\mathit{emp}}$	0.039	0.057	0.045	0.005	0.453	0.339	0.485
			${\widehat{F}}_{SP}$	0.005	0.031	0.031	0.001	0.941	−0.024	0.280
1	0.22,0.08,0.30	250	${\widehat{F}}_{NP}$	0.006	0.031	0.031	0.001	0.940	−0.021	0.284
			${\widehat{F}}_{\mathit{emp}}$	0.040	0.025	0.020	0.003	0.326	0.382	0.230
			${\widehat{F}}_{SP}$	0.010	0.088	0.101	0.008	0.880	0.042	0.977
2	0.02,0.53,0.55	50	${\widehat{F}}_{NP}$	0.028	0.091	0.077	0.010	0.818	0.070	0.984
			${\widehat{F}}_{\mathit{emp}}$	0.151	0.054	0.042	0.028	0.438	−1.364	0.431
			${\widehat{F}}_{SP}$	0.005	0.039	0.038	0.002	0.935	−0.017	0.345
2	0.02,0.53,0.55	250	${\widehat{F}}_{NP}$	0.007	0.041	0.039	0.002	0.930	−0.003	0.404
			${\widehat{F}}_{\mathit{emp}}$	0.149	0.024	0.019	0.025	0.332	−1.338	0.196
			${\widehat{F}}_{SP}$	0.005	0.092	0.118	0.009	0.900	0.034	1.055
3	0.48,0.53,0.80	50	${\widehat{F}}_{NP}$	0.017	0.098	0.088	0.010	0.871	0.062	1.138
			${\widehat{F}}_{\mathit{emp}}$	0.043	0.055	0.043	0.006	0.426	−0.175	0.424
			${\widehat{F}}_{SP}$	0.006	0.040	0.036	0.002	0.897	−0.030	0.348
3	0.48,0.53,0.80	250	${\widehat{F}}_{NP}$	0.007	0.042	0.041	0.002	0.924	−0.024	0.377
			${\widehat{F}}_{\mathit{emp}}$	0.044	0.024	0.020	0.003	0.327	−0.161	0.184

The simulations above show that the SPMLE and NPMLE provide accurate estimates of the survival probabilities under double truncation. We now examine their performance in estimating the difference in survival probabilities between two groups, which is presented in Table 2. For group 1, we simulate n₁ = 50 survival times from a gamma(5,2) distribution, the left truncation time from a gamma(3,1) distribution, and the right truncation time from a gamma(5,2) distribution, which led to 54% of the observations truncated. For group 2, we simulate n₂ = 30 survival times from a gamma(1.5, 4) distribution, the left truncation time from a gamma(1.5,3) distribution, and the right truncation time from a gamma(12.5,1) distribution, which led to 53% of the observations truncated. These distributions were chosen to emulate the features of the AD and FTLD data in Section 4.

Table 2.

Survival timesfor groups 1 and 2 simulated from gamma(5, 2) and gamma(1.5, 4) distributions, respectively. For group 1, left and right truncation times correctly assumed to come from a gamma(3,1) and gamma(5, 2) distribution, respectively, resulting in 54% of the observations truncated. For group 2, left and right truncation times correctly assumed to come from a gamma(1.5, 3) and gamma(12.5, 1) distribution, respectively, resulting in 53% of the observations truncated. The sample sizes are 50 and 30 for groups 1 and 2, respectively. For t = 3, 6, 9,12, we compute the bias, standard deviation (SD), and estimated standard error ($\widehat{SE}$) of Δ₁₂ = ${\widehat{S}}_1$(t) − ${\widehat{S}}_2$(t), which is the difference in survival probabilities between group 1 and group 2 at time t. The true differences between the survival probabilities at time t = 3, 6, 9, 12 are 0.30, 0.42, 0.32, 0.17, respectively.

	SPMLE			NPMLE			eCDF
t	bias(${\widehat{\Delta }}_{12}$)	SD(${\widehat{\Delta }}_{12}$)	$\widehat{\mathrm{SE}}({\widehat{\Delta }}_{12})$	bias(${\widehat{\Delta }}_{12}$)	SD(${\widehat{\Delta }}_{12}$)	$\widehat{\mathrm{SE}}({\widehat{\Delta }}_{12})$	bias(${\widehat{\Delta }}_{12}$)	SD(${\widehat{\Delta }}_{12}$)	$\widehat{\mathrm{SE}}({\widehat{\Delta }}_{12})$
3	−0.01	0.14	0.14	0.01	0.15	0.13	−0.16	0.07	0.04
6	−0.01	0.13	0.13	0.00	0.13	0.13	−0.20	0.11	0.10
9	−0.01	0.15	0.14	0.00	0.15	0.14	−0.21	0.10	0.09
12	0.00	0.16	0.15	0.00	0.17	0.13	−0.14	0.06	0.05

We compare the difference in estimated survival probabilities at time t = 3,6, 9, and 12 based on the SPMLE, NPMLE, and eCDF. Here the estimated survival probability at time t is $\widehat{S}(t)=1-\widehat{F}(t)$. As shown in Table 2, the estimated difference in survival probabilities between groups 1 and 2 at time t, ${\Delta }_{12}={\widehat{S}}_1(t)-{\widehat{S}}_2(t)$, is heavily biased when double truncation is not accounted for. Applying the SPMLE and NPMLE yields estimates with little bias for the difference in survival probabilities between the two groups.

3.1. Robustness to misspecification of truncation distribution

Since ${\widehat{F}}_{SP}$ requires distributional assumptions on the truncation times, we examine the impact of misspecification of the truncation distribution. We again assume L ~ gamma(α₁, β₁), R ~ gamma(α₂, β₂), and T ~ gamma(10,1). However, we now incorrectly specify the right truncation distribution by simulating R ~ Unif[0,20], and correctly specify the left truncation distribution by simulating L ~ gamma(3,1) in model 4. In model 5, we correctly specify the right truncation distribution by simulating R ~ gamma(5,2), and incorrectly specify the left truncation distribution by simulating L ~ Weibull(1, 3). In model 6, we incorrectly specify both the left and right truncation distributions by simulating L ~ Weibull(1, 3) and R ~ Unif [0, 20]. In all models, the proportion of missing data due to left truncation ranged from 0.02 to 0.06, and the proportion of missing data due to right truncation ranged from 0.50 to 0.52. In Web Table 1, we increased the left truncation proportion to a range of 0.22 to 0.33.

Figure 3 displays the bias of ${\widehat{F}}_{SP}$, ${\widehat{F}}_{NP}$, and ${\widehat{F}}_{\mathit{emp}}$ across the 1st through 9th deciles of F₀ for models 4, 5, and 6. The bias of ${\widehat{F}}_{SP}$ was still small in this setting. Table 3 shows that ${\widehat{F}}_{SP}$ still performed as well as ${\widehat{F}}_{NP}$ in terms bias and MSE. Furthermore, misspecification of the truncation distribution only resulted in a slight bias of the median survival time. However the standard error estimates for ${\widehat{F}}_{SP}$ were biased when the right truncation distribution was misspecified. As expected, ${\widehat{F}}_{\mathit{emp}}$ was heavily biased while ${\widehat{F}}_{NP}$ remained unbiased, since neither of these estimators make distributional assumptions about the truncation times. As shown in Web Table 1, the truncation rate does not play a role in the robustness to misspecification of the truncation distribution. We note that in previous literature, the bias of ${\widehat{F}}_{SP}$ was not robust to misspecification of the truncation distribution.^6,7 However the simulations were based on an assumed beta distribution for the truncation times with only one parameter estimated. Here we assumed a gamma distribution with both parameters estimated, which allows more flexibility in estimating different distributions.

Figure 3.

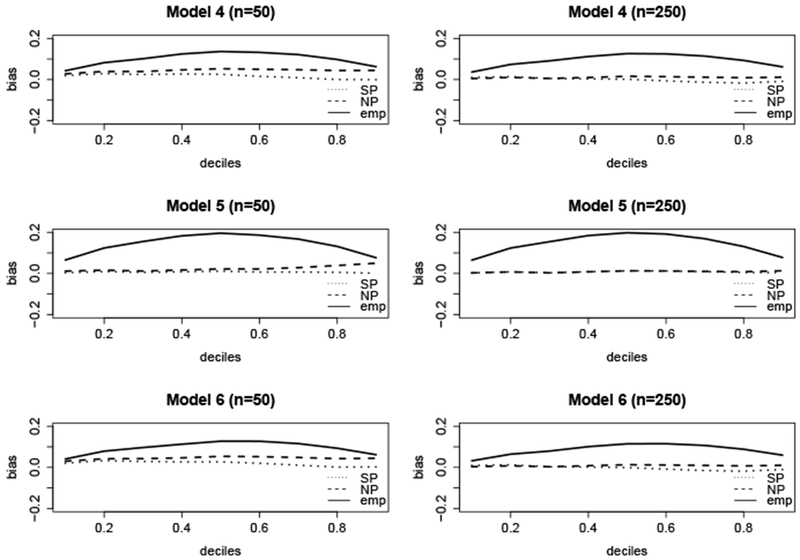
Bias of ${\widehat{F}}_{SP}$ (), ${\widehat{F}}_{NP}$ (), and ${\widehat{F}}_{\mathit{emp}}$ () at t_0.1,…, t_0.9, under misspecification of the truncation distribution. Here t_0.1,…,t_0.9 arethe deciles of the tru survival time distribution F₀, where F₀(t_0.1) = 0.1, F₀(t_0.2) = 0.2, etc.

Table 3.

Simulation results under misspecification of the truncation distribution: Survival times simulated from a gamma(10, 1) distribution. Left and right truncation times assumed to come from a gamma(α₁, β₁) and gamma(α₂, β₂) distribution, respectively. Model 4 corresponds to misspecification of the right truncation time by simulating it as Unif(0, 20), and the left truncation time as gamma(3,1). Model 5 corresponds to misspecification of the left truncation time by simulating it as Weibull(1, 3), and the right truncation time as gamma(5, 2). Model 6 corresponds to misspecification both truncation times by simulating the left truncation time as Weibull(1, 3) and the right truncation time as Unif (0, 20). Here q_L, q_R, q are the proportion of observations missing due to left, right, and double (left and right) truncation, respectively, and n is the size of the observed sample. ${\widehat{F}}_{SP}$ denotes the SPMLE, ${\widehat{F}}_{NP}$ denotes the NPMLE, and ${\widehat{F}}_{\mathit{emp}}$ denotes the naïve empirical CDF which ignores double truncation. These estimators were all computed at t_0.1,…, t_0.9, the 1st through 9th deciles of the true survival distribution F₀. For a given estimator $\widehat{F}$, Bias($\widehat{F}$) is the (absolute) difference between $\widehat{F}$ and F₀, averaged across the 9 deciles. Here SD($\widehat{F}$) is standard deviation of $\widehat{F}$ across simulations, $\widehat{SE}(\widehat{F})$ is estimated standard error of $\widehat{F}$, MSE($\widehat{F},\mathit{MSE}(\widehat{F})$) is mean squared error of $\widehat{F}$, and Cov($\widehat{F}$) is 95% coverage, all averaged across the 9 deciles. Here ${\widehat{t}}_{0.5}$ is the estimated median value based on $\widehat{F}$. The true median value based on F₀ is t_0.5 = 9.7. Here Bias(${\widehat{t}}_{0.5}$) = ${\widehat{t}}_{0.5}$ - t_0.5 and SD(${\widehat{t}}_{0.5}$) is the standard deviation of ${\widehat{t}}_{0.5}$ across simulations.

Model	qL, qR, q	n	Estimator	Bias($\widehat{F}$)	SD($\widehat{F}$)	$\widehat{\mathrm{SE}}(\widehat{F})$	MSE($\widehat{F}$)	Cov($\widehat{F}$)	Bias(${\widehat{t}}_{0.5}$)	SD(${\widehat{t}}_{0.5}$)
			${\widehat{F}}_{SP}$	0.008	0.074	0.160	0.006	0.968	0.091	0.725
4	0.02,0.50,0.51	50	${\widehat{F}}_{NP}$	0.023	0.075	0.068	0.006	0.878	0.017	0.734
			${\widehat{F}}_{\mathit{emp}}$	0.092	0.056	0.044	0.013	0.455	−0.848	0.461
			${\widehat{F}}_{SP}$	0.009	0.033	0.062	0.001	0.995	0.062	0.310
4	0.02,0.50,0.51	250	${\widehat{F}}_{NP}$	0.007	0.033	0.033	0.001	0.932	−0.014	0.299
			${\widehat{F}}_{\mathit{emp}}$	0.091	0.025	0.020	0.010	0.301	−0.816	0.207
			${\widehat{F}}_{SP}$	0.011	0.084	0.098	0.008	0.886	0.032	0.841
5	0.06,0.52,0.56	50	${\widehat{F}}_{NP}$	0.029	0.087	0.077	0.009	0.834	0.073	0.954
			${\widehat{F}}_{\mathit{emp}}$	0.144	0.054	0.042	0.026	0.441	−1.297	0.423
			${\widehat{F}}_{SP}$	0.007	0.038	0.037	0.002	0.921	−0.032	0.339
5	0.06,0.52,0.56	250	${\widehat{F}}_{NP}$	0.008	0.040	0.039	0.002	0.921	−0.021	0.353
			${\widehat{F}}_{\mathit{emp}}$	0.144	0.024	0.019	0.024	0.331	−1.288	0.201
			${\widehat{F}}_{SP}$	0.009	0.073	0.168	0.006	0.961	0.047	0.698
6	0.06,0.50,0.53	50	${\widehat{F}}_{NP}$	0.027	0.073	0.068	0.006	0.873	−0.030	0.659
			${\widehat{F}}_{\mathit{emp}}$	0.088	0.056	0.044	0.012	0.455	−0.826	0.476
			${\widehat{F}}_{SP}$	0.010	0.034	0.062	0.001	0.992	0.035	0.320
6	0.06,0.50,0.53	250	${\widehat{F}}_{NP}$	0.009	0.035	0.032	0.001	0.924	−0.039	0.365
			${\widehat{F}}_{\mathit{emp}}$	0.086	0.025	0.020	0.009	0.301	−0.771	0.210

Sometimes the right truncation time can be written as a function of the left truncation time, as in the cancer data set described in Moreira and de Ũna-Álvarez.⁷ In the Web Appendix, we study the case R = L + d₀, where d₀ is a constant. As shown in Web Table 2, the SPMLE and NPMLE have little bias when the truncation distribution is correctly specified, while the eCDF is biased. Furthermore, the SPMLE is still robust to misspecification of the truncation distribution in this setting.

3.2. Robustness to independence violation between survival and truncation times

Both ${\widehat{F}}_{SP}$ and ${\widehat{F}}_{NP}$ assume the survival and truncation times are independent. However this may not always be the case in practice. We therefore examine the robustness of these estimators when this independence assumption is violated. We simulate the survival and truncation times from a normal copula. The marginal distributions for the survival, left, and right truncation times are set to gamma(10,1), gamma(4,1.5), and gamma(8,1.5) distributions, respectively. Let ρ_XY denote the correlation between random variables X and Y. In model 7, we set ρ_LT = 0.5, ρ_LR = 0.1, and ρ_TR = 0.1. In model 8, we set ρ_LT = −0.5, ρ_LR = 0.1, and ρ_TR = −0.1. These correlations lead to strong positive dependence (model 7) and strong negative dependence (model 8) between the left truncation times and survival times. We set ρ_LT = −0.1, ρ_LR = 0.1, and ρ_TR = −0.5 in model 9, which leads to strong negative dependence between the survival times and right truncation times. In model 10, we set ρ_LT = −0.5, ρ_LR = 0.1, and ρ_TR = −0.5, which leads to strong negative dependence between both the survival times and left truncation times as well as the survival times and right truncation times.

Figure 4 displays the bias of ${\widehat{F}}_{SP}$, ${\widehat{F}}_{NP}$, and ${\widehat{F}}_{\mathit{emp}}$ across the 1st through 9th deciles of F₀ for models 7 through 10. All three estimators are biased. Under weaker dependence between the survival time and right truncation time (i.e. models 7 and 8), the bias of ${\widehat{F}}_{SP}$ and ${\widehat{F}}_{NP}$ are smaller compared to models 9 and 10, where there is a strong dependence between the survival time and right truncation time. As Table 4 shows, the coverage probabilities in all models are extremely poor.

Figure 4.

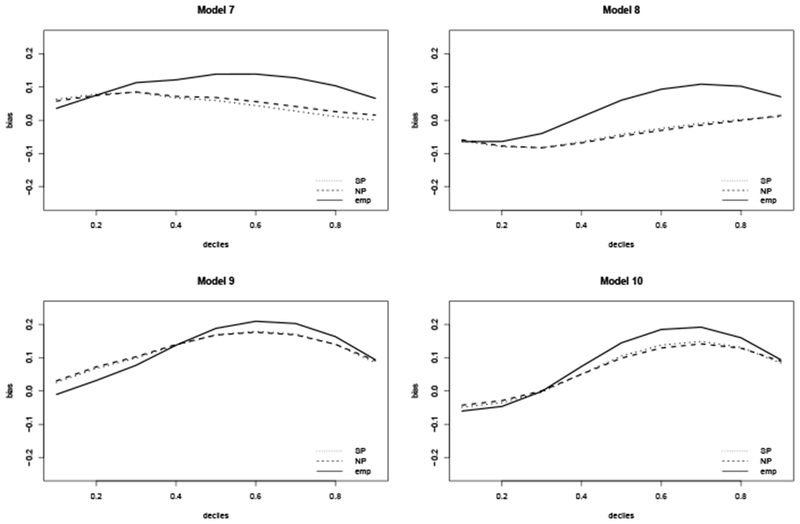
Bias of ${\widehat{F}}_{SP}$ (), ${\widehat{F}}_{NP}$ (), and ${\widehat{F}}_{\mathit{emp}}$ () at t_0.1,…, t_0.9, under violation of independence between the survival and truncation times. Here t_0.1, …, t_0.9 arethe deciles of the true survival time distribution F₀, where F₀(t_0.1) = 0.1, F₀(t_0.2) = 0.2, etc.

Table 4.

Simulation results under violation of the independence assumption: Survival and truncation times simulated from a normal copula with correlations ρ_LT , ρ_LR, and ρ_TR, where ρ_XY denotes the correlation between random variables X and Y. The marginal distributions for the survival, left, and right truncation times are set to gamma(10, 1), gamma(3, 1), and gamma(5, 2) distributions, respectively. Here q_L,q_R, q are the proportion of observations missing due to left, right, and double (left and right) truncation, respectively. The average observed sample size is n = 250 for all models. ${\widehat{F}}_{SP}$ denotes the SPMLE, ${\widehat{F}}_{NP}$ denotes the NPMLE, and ${\widehat{F}}_{\mathit{emp}}$ denotes the naïve empirical CDF which ignores double truncation. These estimators were all computed at t_0.1, …, t_0.9, the 1st through 9th deciles of the true survival distribution F₀. For a given estimator $\widehat{F}$, Bias($\widehat{F}$) is the (absolute) difference between $\widehat{F}$ and F₀, averaged across the 9 deciles. Here SD($\widehat{F}$) is standard deviation of $\widehat{F}$ across simulations, $\widehat{SE}(\widehat{F})$ is estimated standard error of $\widehat{F}$, $\mathit{MSE}(\widehat{F})$ is mean squared error of $\widehat{F}$, and Cov($\widehat{F}$) is 95% coverage, all averaged across the 9 deciles. Here ${\widehat{t}}_{0.5}$ is the estimated median value based on $\widehat{F}$. The true median value based on F₀ is t_0.5 = 9:7. Here Bias(${\widehat{t}}_{0.5}$) = ${\widehat{t}}_{0.5}$ - t_0.5 and SD(${\widehat{t}}_{0.5}$) is the standard deviation of ${\widehat{t}}_{0.5}$ across simulations.

Model	ρLT, ρLR, ρRT	qL, qR, q	Estimator	Bias($\widehat{F}$)	SD($\widehat{F}$)	$\widehat{SE}(\widehat{F})$	MSE($\widehat{F}$)	Cov($\widehat{F}$)	Bias(${\widehat{t}}_{0.5}$)	SD(${\widehat{t}}_{0.5}$)
			${\widehat{F}}_{SP}$	0.049	0.038	0.046	0.005	0.744	−0.458	0.343
7	0.5,0.1,0.1	0.09,0.35,0.43	${\widehat{F}}_{NP}$	0.055	0.038	0.024	0.005	0.380	−0.507	0.332
			${\widehat{F}}_{\mathit{emp}}$	0.102	0.025	0.020	0.012	0.315	−0.896	0.202
			${\widehat{F}}_{SP}$	0.042	0.033	0.046	0.004	0.701	0.336	0.268
8	−0.5,0.1,−0.1	0.22,0.37,0.56	${\widehat{F}}_{NP}$	0.044	0.034	0.022	0.004	0.447	0.374	0.276
			${\widehat{F}}_{\mathit{emp}}$	0.068	0.023	0.018	0.006	0.293	−0.285	0.171
			${\widehat{F}}_{SP}$	0.119	0.029	0.058	0.018	0.478	−0.968	0.218
9	−0.1,0.1,−0.5	0.18,0.39,0.55	${\widehat{F}}_{NP}$	0.121	0.029	0.026	0.018	0.101	−0.982	0.223
			${\widehat{F}}_{\mathit{emp}}$	0.124	0.022	0.017	0.021	0.262	−0.942	0.156
			${\widehat{F}}_{SP}$	0.083	0.027	0.055	0.010	0.579	−0.503	0.189
10	−0.5,0.1,−0.5	0.22,0.39,0.58	${\widehat{F}}_{NP}$	0.079	0.028	0.025	0.009	0.279	−0.488	0.195
			${\widehat{F}}_{\mathit{emp}}$	0.106	0.021	0.017	0.016	0.223	−0.638	0.146

In Web Table 3, we reexamine this situation under very mild left truncation and severe right truncation. In models C.1 and C.2, the bias of ${\widehat{F}}_{SP}$ and ${\widehat{F}}_{NP}$ is minimal because of the following: Despite a strong dependence between the left truncation time and survival time, the left truncation rate is minimal. In addition, the dependence between the right truncation time and survival time is minimal. When the dependence between the right truncation time and survival time is stronger (models C.3 and C.4), these estimators are heavily biased. In Web Table 4, we study the case R = L + d₀ when L and T are dependent. All estimators are heavily biased with poor coverage probabilities in this setting.

4. Case study: Autopsy-confirmed Alzheimer’s disease and frontotemporal lobar degeneration

Our motivating example comes from autopsy-confirmed data on individuals with either AD or FTLD retrieved from the neurodegenerative disease autopsy program at the University of Pennsylvania between 1995 and 2012. The target sample for the research purposes of the study consists of all individuals with either AD or FTLD onset before 2012, who either entered the program between 1995 and 2012, or would have entered the program between 1995 and 2012, had they not succumbed to the disease beforehand. Our observed sample contains all individuals who entered the program between 1995 and 2012, and had an autopsy-confirmed diagnosis of AD or FTLD before 2012. Individuals with AD or FTLD who met the study criteria but died before entering the program were not observed, yielding left truncated data. Furthermore, observations were only obtained from individuals who had an autopsy-confirmed diagnosis of AD or FTLD. Individuals who lived past the end of study date were not diagnosed, and therefore not included in our sample. Thus our data is also right truncated. Our data consists of 47 autopsy-confirmed AD subjects and 31 autopsy-confirmed FTLD subjects. The survival time of interest (T) is the time between disease symptom onset and death. The left truncation time (L) is the time between disease symptom onset and entry into the study (i.e. initial clinic visit). The right truncation time (R) is the time between disease symptom onset and the end of the study, which is taken to be July 1, 2012. Due to double truncation, we only observe individuals with L ≤ T ≤ R.

Our goal is to estimate and compare the survival distributions for these two groups. Before we apply the SPMLE or NPMLE to estimate the survival distributions for AD and FTLD, we must test whether the survival times are independent of the truncation times for each group. We test this assumption using the test statistic introduced in Martin and Betensky.⁸ The resulting tests did not reject the null hypothesis of independence at the α = 0.05 level for either the AD or FTLD group. We justify the identifiability constraints, a_HL < a_F < a_HR and b_HL < b_F < b_HR, in Web Appendix A. We can therefore proceed to apply the methods described in Section 2 to our data.

The NPMLE and eCDF were computed without any parametric assumptions on the survival or truncation times. For the AD group, the SPMLE was computed by assuming that the left truncation time has a gamma(α₁, β₁) distribution and the right truncation time has a gamma(α₂, β₂) distribution. The SPMLE for the FTLD group was estimated independently of the AD group, and assumed that the left truncation time has a gamma(θ₁, γ₁) distribution and the right truncation time has a gamma(θ₂, γ₂). The distribution of the truncation times was chosen by examining an external data set of individuals with clinically diagnosed AD and FTLD. As shown by the simulation studies in Section 3 and the Web Appendix, the choice of the two parameter gamma distribution leads to more robust estimators. Under these parametric assumptions, we have (${\widehat{\alpha }}_1=2.9$, ${\widehat{\beta }}_1=1.1$), (${\widehat{\alpha }}_2=5.2$, ${\widehat{\beta }}_2=1.9$), (${\widehat{\theta }}_1=1.7$, ${\widehat{\gamma }}_1=3.1$), and (${\widehat{\theta }}_2=12.7$, ${\widehat{\gamma }}_2=1.1$). Based on these results, the probability of truncation for an individual with AD and FTLD was estimated to be 0.58 and 0.54, respectively.

To check whether the choice of the gamma distribution is appropriate, we test the null hypothesis H₀ : K = K_θ, independently for the AD and FTLD group, using a Kolmogorov-Smirnov type test statistic.¹⁶ The resulting test did not reject H₀ at the α = 0.05 level for either AD or FTLD, and therefore we do not have enough evidence against the gamma distribution assumptions for the truncation times in either group.

The estimated survival curves $\widehat{S}(t)=1-\widehat{F}(t)$ based on the SPMLE, NPMLE, and eCDF are plotted in Figure 5. In the top left panel, we compare these three estimators for the AD group. The estimated survival probabilities based on the SPMLE and NPMLE are similar, and are greater than those based on the eCDF. This implies that right truncation had a greater impact than left truncation in the AD group. In other words, a greater proportion of subjects survived past the end of the study date compared to surviving past their study entry date. The top right panel compares these estimators for the FTLD group. Here the estimated survival probabilities based on the SPMLE and NPMLE are also similar, but are less than those based on the eCDF. This implies that left truncation had a greater impact than right truncation in the FTLD group. In other words, a smaller proportion of subjects survived past the end of the study date compared to surviving past their study entry date.

Figure 5.

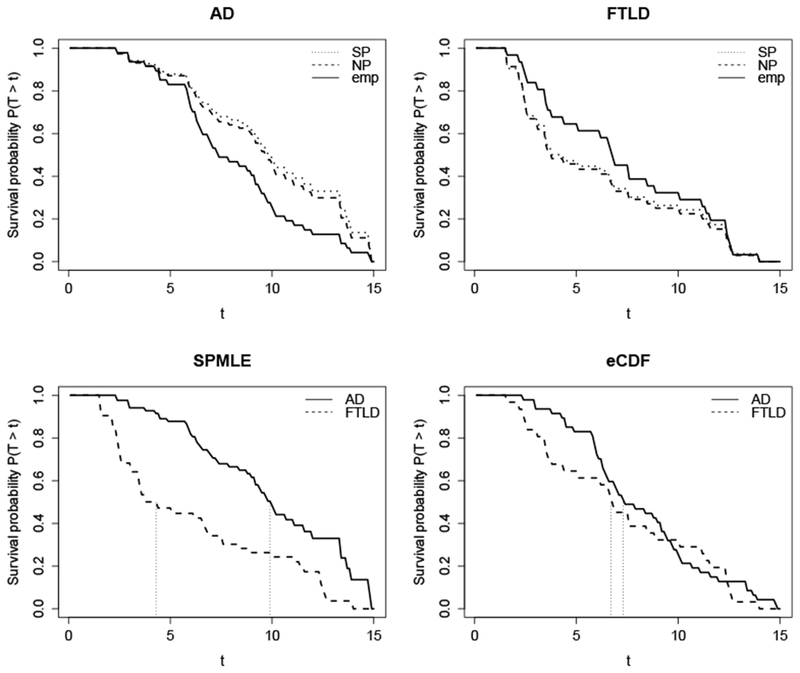
Top row: Estimated survival curves for AD (top left panel) and FTLD (top right panel) based on ${\widehat{F}}_{SP}$ (), ${\widehat{F}}_{NP}$ (), and ${\widehat{F}}_{\mathit{emp}}$ (). Bottomrow: Comparing AD () and FTLD () survival curves based on the SPMLE ${\widehat{F}}_{SP}$ (bottom left panel) and eCDF ${\widehat{F}}_{\mathit{emp}}$ (bottom right panel). Vertical dotted lines represent median survival times for each group.

The bottom row of Figure 5 compares the AD and FTLD survival probabilities based on the SPMLE (left) and the eCDF (right). When we do not adjust for double truncation, the eCDF concludes that the survival curves of AD and FTLD are nearly identical, with median survival times less than 1 year apart (AD = 7.3 years, FTLD = 6.7 years). When we adjust for the double truncation, the survival probabilities for AD are greater than those of FTLD. Furthermore, the difference in median survival time is now greater than 5 years (AD = 9.9 years, FTLD = 4.3 years).

We test for equality of the distribution functions of AD and FTLD using Bilker and Wang’s semiparametric extension of the Mann-Whitney test.² The resulting U-statistic is $\widehat{U}=2.62$ with variance ${\widehat{V}}_{\widehat{U}}=2.81.\widehat{U}>0$ gives evidence that the survival curve for AD is greater than that for FTLD. However this result is not statistically significant (p-value = 0.12). We note that the standard log-rank test (ignoring truncation) resulted in a p-value of 0.46.

The Mann-Whitney test above tests whether two survival curves are equal. We now test for a difference in survival probabilities between AD and FTLD at specific time points. The results are provided in Table 5. When we adjust for double truncation, we conclude that the AD group has a greater survival probability than the FTLD group at years 3, 6 and 9. While the probability of survival at 12 years is also greater for the AD group, the resulting test is not statistically significant (p=0.221). When we do not account for double truncation, we find no significant difference in the survival probabilities. Note the results in Table 5 closely match the results from the simulation study displayed in Table 2.

Table 5.

Case study results: Testing equality of survival probabilities between AD and FTLD at year t =3, 6, 9, and 12. $\widehat{S}(t)=1-\widehat{F}(t)$ is survival probability at t, ${\widehat{SE}}_t$ is the estimated standard error at time t, W_t is the Wald statistic comparing the survival probability between AD and FTLD at time t.

		AD	FTLD
t	Estimator	$\widehat{S}(t)({\widehat{\mathrm{SE}}}_t)$	$\widehat{S}(t)({\widehat{\mathrm{SE}}}_t)$	Wt	p-value
3	SPMLE	0.94 (0.04)	0.64(0.11)	6.80	0.009
	NPMLE	0.93 (0.03)	0.62(0.12)	6.45	0.011
	eCDF	0.94 (0.04)	0.81 (0.07)	2.67	0.102
6	SPMLE	0.81 (0.06)	0.45 (0.10)	9.58	0.002
	NPMLE	0.79 (0.06)	0.43 (0.12)	7.05	0.008
	eCDF	0.70 (0.07)	0.61 (0.09)	0.66	0.417
9	SPMLE	0.62 (0.09)	0.26 (0.08)	8.56	0.003
	NPMLE	0.60 (0.08)	0.25 (0.09)	7.50	0.006
	eCDF	0.40 (0.07)	0.32 (0.08)	0.55	0.459
12	SPMLE	0.33 (0.11)	0.17 (0.07)	1.50	0.221
	NPMLE	0.30 (0.08)	0.15 (0.07)	1.28	0.258
	eCDF	0.13 (0.05)	0.19 (0.07)	0.59	0.444

5. Discussion and Recommendations

Due to the inaccuracy of clinical diagnoses and lack of available biomarkers, many studies of neurodegenerative diseases rely on autopsy-confirmed diagnoses. The aim of this paper was to raise awareness of the selection bias in these studies and highlight appropriate methods to account for it. We described how the selection bias arises due to the inherent double truncation in these studies and showed that ignoring it leads to biased estimators of the survival time distribution. To adjust for double truncation, we applied semiparametric and nonparametric maximum likelihood estimators of the survival time distribution. We conducted extensive simulation studies to evaluate the performance of these estimators in a variety of settings, and applied these estimators in a case study of autopsy-confirmed AD and FTLD individuals.

The simulation studies confirmed that the SPMLE and NPMLE had little bias in small samples, while the naïve empirical CDF which ignores double truncation was heavily biased. We also found that the empirical CDF had a much larger mean squared error relative to the SPMLE and NPMLE under moderate to severe truncation. Furthermore, the 95% confidence intervals of the empirical CDF were well below the nominal level, while those corresponding to the SPMLE and NPMLE were close to the nominal level under larger sample sizes.

When applied to our autopsy-confirmed data set, the survival probabilities based on the SPMLE and NPMLE were significantly greater for the AD group relative to the FTLD group at almost all time points. Furthermore, the difference in median survival time between AD and FTLD was over 5 years. Application of the empirical CDF (i.e. the standard method ignoring double truncation) to the AD and FTLD groups found that the survival probabilities were similar between the two groups, with median survival time less than one year apart. These analysis findings were supported by simulations that emulate this case study data set, which validate the appropriateness of accounting for double truncation in the analysis.

We recommend the approach taken in our data example when estimating the survival time distribution of an autopsy-confirmed neurodegenerative disease, since this approach leads to consistent estimators with lower mean-squared errors than the standard methods. Our approach consisted of first testing for independence between the survival times and truncation times, as well as justifying identifiability constraints. We then applied the SPMLE and NPMLE of the survival distribution function to the data. Based on our simulations and previous simulations,^6,7 the SPMLE has a lower standard error and MSE than the NPMLE, and is therefore a more efficient estimator. However the SPMLE requires the correct distribution of the truncation times. Although incorrectly specifying the truncation distribution did not result in biased estimators of the survival time distribution in our simulation study, this is not always the case.^6,7 We therefore recommend testing the parametric assumptions of the SPMLE using the test statistics provided in Moreira et al.¹⁶

The main limitation with the methods described in this paper is that they require independence of the truncation and survival times. This is not always a realistic assumption in individuals with neurodegenerative diseases. Our simulation studies showed that the estimators which adjust for double truncation are sensitive to this independence assumption. Therefore these estimators must be used with caution. While methods exist to test this independence assumption,⁸ an extension of these methods is needed to adjust for dependent truncation times and survival times.

The double truncation inherent in autopsy-confirmed studies of neurodegenerative diseases and methods to correct for it have so far received little attention in the literature. In this paper, we showed that ignoring double truncation leads to biased estimators of the survival time distribution, and outlined methods to adjust for it. The effects of ignoring double truncation in these studies was highlighted in our data example. Given the devastating effects of neurodegenerative diseases on patients, their caregivers, and society, it is imperative to adjust for double truncation in order to have accurate knowledge of the survival time distribution.

6. Data Accessibility

Code associated with this paper will be available for archiving at the journal’s repository. Functions to compute the NPMLE of the survival time distribution and test for independence between the survival and truncation times are also provided in the ”SurvTrunc” package, which is available in the CRAN R library. The data are not publicly available due to privacy or ethical restrictions.

7. Supporting Web Materials

Web appendices, including justification of the identifiability constraints for our case study (Web Appendix A), and additional results from simulation studies (Web Tables 1–4) referenced in Section 3, are available alongside the online version of this article.