Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2010 Jan 20;30(3):958–962. doi: 10.1523/JNEUROSCI.3742-09.2010

Motor Cortical Representation of Hand Translation and Rotation during Reaching

Wei Wang 1,2, Sherwin S Chan 2, Dustin A Heldman 2, Daniel W Moran 2,✉
PMCID: PMC6633081  PMID: 20089904

Abstract

Previous studies have shown that hand translation is well represented by neuronal activity in the proximal arm area of primary motor cortex (M1). However, little is known about cortical representation of hand rotation in M1. In this study, single-unit activity was recorded from monkeys while they performed a “center-out with rotation” task. When reaching for a target, subjects had to match four separate kinematic parameters: three-dimensional location and one-dimensional orientation of the target. Among the 512 neurons modulated by hand movement, 446 were tuned to hand translation, 326 were tuned to hand rotation, and 260 neurons were tuned to both hand translation and hand rotation. Approximately half of the neurons that encoded both translation and rotation did so in a nonlinear manner. This nonlinear interaction can be modeled as a gain-field type of encoding whereby hand rotational velocity modulated the hand translational cosine tuning curves in a multiplicative manner. Furthermore, this study demonstrated that both hand translation and hand rotation can be decoded simultaneously from a population of motor cortical neurons.

Introduction

Common acts of daily living require precise control of our hands. We must not only accurately control the three-dimensional (3D) location of our hands but also its 3D orientation in space (i.e., yaw, pitch, and roll). Furthermore, since our hands are coupled to our bodies via the musculoskeletal system, we ultimately are controlling limb dynamics to position/orient our hands in space. Thus, from a motor control point of view, the brain must contain not only position/orientation information but also their time derivatives (i.e., 3D translational velocity and 3D rotational velocity), yielding a total of 12 independent kinematic control parameters (Bernstein, 1935). Motor cortical representation of hand translation during reaching has been studied extensively, demonstrating that both hand translational velocity and position can be reconstructed from the activities of a population of M1 neurons (Georgopoulos et al., 1982, 1986; Kettner et al., 1988; Schwartz et al., 1988; Ashe and Georgopoulos, 1994; Fu et al., 1995; Kakei et al., 1999; Moran and Schwartz, 1999; Paninski et al., 2004; Wang et al., 2007).

While hand position/translation has been well studied, hand orientation/rotation has received limited attention. One exception is a study by Kakei et al. (1999) examining M1 neuronal activity while monkeys performed a novel 2D center-out task with wrist movement. Their experiment, performed with three different forearm postures (pronation, neutral, and supination), was originally designed to investigate whether M1 neurons encode muscle activity or hand movement direction. Interestingly, neural activity was modulated by forearm posture for approximately two-thirds of the neurons encoding hand movement direction. Since hand orientation in the frontal plane covaried with forearm posture in their study, it can be postulated that those neurons might encode both translational movement direction and hand orientation. Furthermore, this suggests that there might be a common pool of neurons in the proximal arm area of M1 that control both hand translation and hand rotation.

Materials and Methods

Experiment setup.

The experimental paradigm, surgical procedures, neurophysiological recordings, and daily animal care were approved by the Washington University Animal Studies Committee, and followed all guidelines set by the Association for Assessment and Accreditation of Laboratory Animal Care and the Society for Neuroscience.

Two monkeys (Macaca fascicularis) were operantly trained to perform reaching tasks within a virtual reality simulator (VR) (Wang et al., 2007). The monkeys sat in a custom-made primate chair while real-time 3D images were generated by a graphics workstation (Silicon Graphics) and presented to the animal via 3D monitor (Dimension Technologies). An optoelectronic tracking system (Northern Digital, Optotrak 3020) was used to track the 3D position of three markers arranged in a triangular pattern on the dorsum of the monkey's hand. The coordinates of the three markers defined a rigid body and were used to calculate both the 3D location and orientation of the hand in the workspace in real time and were fed back to the graphics workstation. Additionally, the coordinates of the three markers as well as the location and orientation of the hand rigid body were sampled (100 Hz) and stored in a data file. The monkeys performed reaching tasks within the computer controlled environment and received a liquid reward after each successful trial.

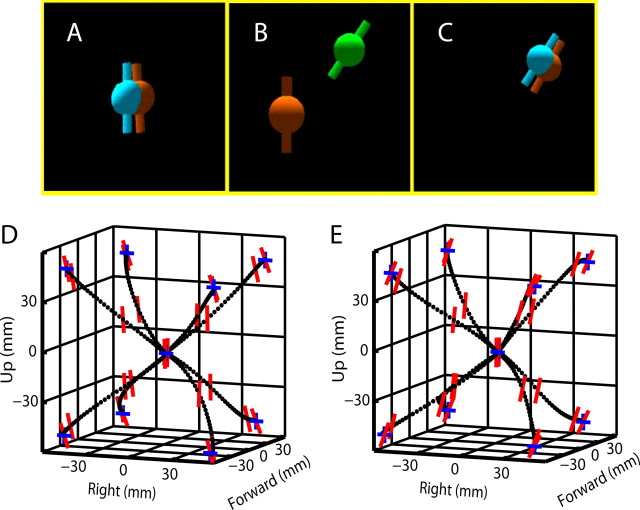
The monkeys performed a modified version of the 3D center-out reaching task (Georgopoulos et al., 1986), the “center-out with rotation” task, in which the monkeys had to not only reach to specific 3D locations but also had to rotate their hands during the reach to match the orientation of the target (Fig. 1). At the beginning of this task, a target appeared at the center of the workspace with a neutral (0°) orientation. The monkey captured this center target with the cursor sphere by matching both the location and orientation and holding it for a random interval between 500 and 1000 ms. Next, the center target disappeared, and one of the eight peripheral targets appeared with one of three different orientations (−35, 0, or 35° of roll). These eight targets were located at the eight corners of a virtual cube (10 cm sides). The 24 possible target locations/orientations were presented in a pseudorandom order, and the monkey had to reach the target with the proper hand orientation and remain there for a second random hold period (200–300 ms) to make a successful reach. Four repetitions were made for each target/orientation yielding a total of 96 reaches for each cell analyzed in this study.

Figure 1.

Figure 1.

Open in a new tab

Center-out with rotation task and hand kinematics. The subject's 3D hand position and hand orientation in the frontal plane were mapped directly to the position and orientation of the orange cursor in the virtual reality simulator. A, The subject started each movement from a center target with vertical orientation. B, In this example, the subject reached for a target at the forward, upper, and right corner of the workspace with clockwise rotation of the hand. C, The monkey captured the target. D, E, Average 3D hand trajectory and hand orientation in the frontal plane for eight peripheral targets with counterclockwise and clockwise rotation, respectively. Position of the black dots represents the instantaneous 3D hand position. Orientation of the small red vertical lines indicates hand orientation in the frontal plane at four time points: start of movement, one-third into movement, two-thirds into movement, and end of movement (length of the small vertical line is arbitrary). At the time points corresponding to start and end of movement, blue “+” signs were plotted to indicate the horizontal and vertical directions to facilitate the visualization of hand rotation. Hand kinematics was also plotted as a function of time in supplemental Figure 8 (available at www.jneurosci.org as supplemental material). Note that hand translation and rotation occurred simultaneously, as further demonstrated by supplemental Figures 1 and 2 (available at www.jneurosci.org as supplemental material).

After the monkeys were well trained, a circular stainless steel recording chamber with an inner diameter of 16 mm was implanted over the contralateral primary motor cortex. Standard stereotaxic technique was used to center the recording chamber over the gyrus of proximal arm area of primary motor cortex (rostral M1). Recording electrodes were mounted in a 16 channel microdrive (Ekhorn System, Thomas RECORDING) and arranged into a linear array with interelectrode spacing of ∼300 μm. Each electrode could be moved independently with a precision of 1 μm (Baker et al., 1999). Single-unit activities were sorted with time-amplitude windows using customized spike-sorting software (OpenProject 1.5, Tucker-Davis Technologies). After the units were isolated, the subject performed the center-out with rotation task followed by an exam to determine whether each neuron responded to passive manipulation of either the shoulder or elbow of the contralateral arm.

Interaction between cortical representations of hand translation and rotation.

This analysis focused on neuronal firing rates averaged over reaction and movement time (i.e., from target onset to movement offset) calculated using the partial binning method (Richmond et al., 1987; Reina et al., 2001; Wang et al., 2007). For each neuron, a two-way ANOVA was performed using hand translation and hand rotation as two factors (eight translation directions and three rotation conditions). This analysis was used to examine whether a motor cortical neuron is modulated by hand translation and/or hand rotation, as well as whether there was a multiplicative interaction between hand translation and rotation. A p value <0.05 indicates significant modulation. Furthermore, for all neurons modulated by hand translation, the preferred translational direction (PD) was calculated by regressing neuronal firing rates to hand translation (Georgopoulos et al., 1986; Reina et al., 2001).

To directly visualize the nonlinear interaction between hand translation and rotation, the current study examined the effect of hand rotation on translational tuning curve (i.e., neuronal activity as a function of hand translation direction) at both individual neuron and population levels. For each individual neuron, three translational tuning curves were built by plotting neuronal firing rates as a function of hand translation direction, one for each rotation condition. For the population level analysis, individual neuronal firing rate data were first normalized by their root-mean-square value across all trials. The normalized neuronal firing rate data from all neurons with significant interaction between hand translation and rotation were then sorted into 20° bins from 0 to 180° based on the projected angle (α) between hand translation direction and the PD of the respective neuron. Essentially, for each trial, the angle (α) was calculated, and, depending on the value of the angle (α), the corresponding neuronal firing rate value was sorted into a specific 20° bin. This procedure creates three population-level translation direction tuning curves, one for each rotation condition. For each condition, the normalized neuronal activities were fitted with the standard cosine tuning function (Georgopoulos et al., 1986; Wang et al., 2007):

graphic file with name zns00310-7590-m01.jpg

where f is the neural activity and θ is the angle between hand translation direction and PD. b0 represents the baseline cortical activity, and b1 is the amplitude of the cosine curve or the depth of modulation. Changes in b0 would shift the tuning curve vertically representing an additive effect of hand rotation on hand translation direction tuning, and changes in b1 would scale the tuning curve and represent a multiplicative or gain field effect of hand rotation on hand translation direction tuning. Furthermore, the 95% confidence interval (CI) of depth of modulation was calculated to determine whether there is any statistically significant difference in depth of modulation among different hand rotation conditions.

Temporal dynamics of cortical activity representing hand orientation and rotation.

For the behavioral paradigm used in the current study, the average hand rotational velocity and average hand orientation are correlated (i.e., they have the same sign/direction), hence, analysis using neuronal activity averaged over reaction and movement time will not be sufficient to differentiate neuronal activities encoding hand orientation from those encoding hand rotational velocity. Since hand orientation and hand rotation have different temporal profiles during the center-out with rotation movement (ramp for hand orientation vs bell-shape curve for hand rotational velocity), temporal dynamics of neuronal activity were further examined using a multibin analysis approach. Movement time was identified based on the speed profiles of both hand translation in 3D space and hand rotation in the frontal plane, and it encompasses both translational and rotational movements. For each trial, the movement time was divided into 40 equal time bins. Then, 30 premovement bins and 30 postmovement bins were defined with the same bin width (Reina et al., 2001; Wang et al., 2007), resulting in 100 time bins for each trial. Firing rates of individual neurons were calculated for each bin using the partial binning method to generate a time series of instantaneous neuronal firing rates (Richmond et al., 1987; Wang et al., 2007), which was then low-pass filtered with a cutoff frequency of 10 Hz. For each neuron, the baseline component was computed by averaging the neural activity across all trials (Moran and Schwartz, 1999) and subtracted from the total neuronal activity time series. For each neuron, firing rate data from trials with the same rotation condition but different translation directions were averaged to remove neuronal activities related to hand translation. The resulted firing rate data were then rectified, normalized by the root-mean-square value of respective neurons and averaged across all neurons to examine the temporal profile of motor cortical activity encoding hand rotation.

Simultaneous decoding of hand translation and hand rotation in four-dimensional space.

The current study decoded continuous 3D hand translation and hand rotation in the frontal plane over time using the multibin neuronal firing rate data by using a modified version of the population vector algorithm (Georgopoulos et al., 1986), the indirect optimal linear estimator (OLE) method (Wang et al., 2007). Briefly, for each neuron, the preferred rotation direction was set to −1 if the neuron preferred clockwise (CW) rotation and 1 if the neuron preferred counterclockwise (CCW) rotation. The 3D preferred translation direction and 1D preferred rotation direction made up a 4D “preferred movement” vector for an individual neuron. The optimal decoding weights were obtained by taking the pseudoinverse of the matrix that is composed of all the preferred movement vectors of motor cortical neurons used in decoding (Wang et al., 2007). The optimal decoding weights were then applied to the instantaneous firing rate data. To decode hand translation, neurons tuned to translation only and neurons tuned to both translation and rotation were used. Similarly, neurons tuned to rotation only and neurons tuned to both translation and rotation were used to decode hand rotation.

Results

Two monkeys (Macaca fascicularis) were operantly trained to perform this “center-out with rotation” task, with the average 3D hand trajectories and orientations shown in Figure 1 and supplemental Figure 1 (available at www.jneurosci.org as supplemental material). A key feature of hand kinematics was that both translational and rotational movements were involved and tightly coupled in time, i.e., translation and rotation occurred simultaneously, making it possible to study the interaction between the motor cortical representations of the two different types of movement (supplemental Fig. 2, available at www.jneurosci.org as supplemental material).

Single-unit activities were recorded from the gyrus of the proximal arm area of primary motor cortex (rostral M1) contralateral to the performing arm. This study focused on the average neuronal firing rate from cue onset to the end of the movement. To test whether a M1 neuron was modulated by hand translation or hand rotation and whether there is a nonlinear interaction between cortical representations of those two types of movements, a two-way ANOVA was used to compare neuronal firing rates under eight different translation conditions and three different rotation conditions (CW, no rotation, and CCW). Overall, 512 (64%) out of the 806 neurons recorded in this study were modulated by hand movement (supplemental Fig. 3, available at www.jneurosci.org as supplemental material). Among those movement-modulated neurons, 446 (87%) were modulated by hand translation, 326 (64%) were modulated by hand rotation, and 260 (51%) were modulated by both. Furthermore, the two-way ANOVA test indicates that 131 (26%) neurons were significantly modulated by both hand translation and hand rotation in a nonlinear manner. Figure 2 shows the spike rasters of two representative neurons with both translational and rotational tuning. The spatial distributions of three types of neurons (tuned to hand translation only, tuned to hand rotation only, and tuned to both) were plotted in supplemental Figure 4 (available at www.jneurosci.org as supplemental material), and there is no significant difference in spatial distribution among these three different groups of neurons recorded in this study.

Figure 2.

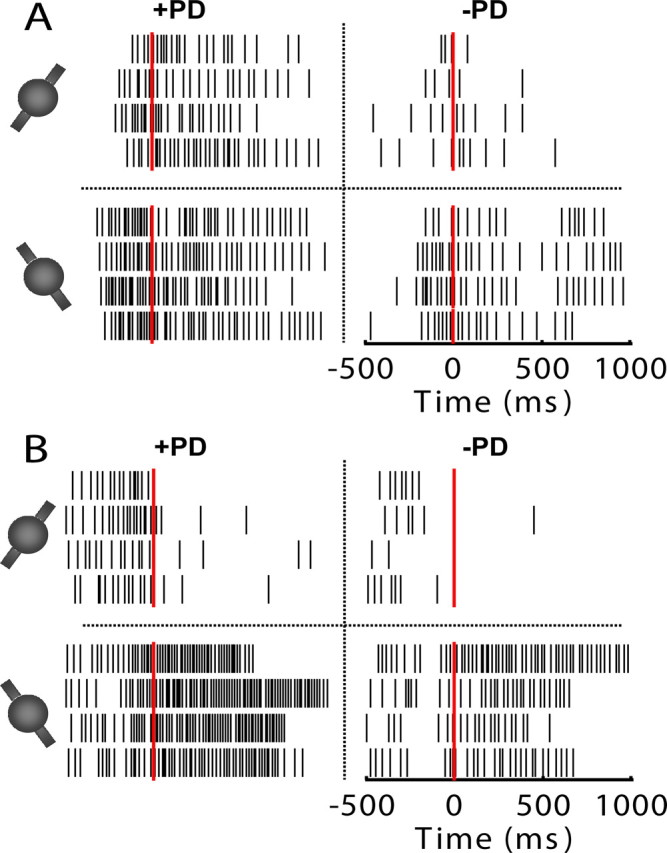
Figure 2.

Open in a new tab

Spike rasters of two representative motor cortical neurons tuned to both translation and rotation from two separate monkeys (A, B). All rasters are aligned to movement onset time (time 0, red line). Thin black vertical lines indicate occurrences of spikes from 0.5 s before movement onset to 1 s after movement onset. Rasters are divided into four groups by the dotted lines. Those four groups correspond to four targets, i.e., four different combinations of translation and rotation. The top and bottom rows correspond to movements with CW and CCW rotations, respectively. The left and right columns correspond to movements along the preferred translational direction (+PD) and movements opposite to the preferred translational direction (−PD), respectively. Difference in spike rate between the left and right columns indicates translational tuning, while difference in spike rate between the top and bottom rows indicates rotational tuning.

Previously, it was demonstrated that both hand position and velocity signals are encoded by M1 neurons during translational movements, with the velocity signal being more salient than the position signal (Wang et al., 2007). Thus, it is expected that both hand orientation and rotational velocity should be represented in M1 activity. To confirm this hypothesis, the temporal evolution of neural activity during the center-out with rotation movement was examined. The spike data were binned into instantaneous firing rates, and their baseline components were removed. For each neuron, firing rates corresponding to movements with identical rotations but different translational directions were averaged to remove the effect of translational encoding. Next, changes in firing rate were rectified and averaged across all neurons tuned to hand rotation to yield a population response. Analogous to translational results from a previous study (Wang et al., 2007), the average M1 neuronal response showed a temporal profile indicating that rotational velocity was the dominant parameter being encoded with orientation angle also being encoded but to a lesser degree (supplemental Fig. 5, available at www.jneurosci.org as supplemental material).

This study has found that single M1 neurons are capable of simultaneously encoding hand position, translational velocity, orientation, and rotational velocity. When two or more physical variables are encoded by the same neuron, their relationship can be either linear (i.e., additive model) or nonlinear (e.g., multiplicative model or gain field). Previously, it was shown that a single M1 neuron can encode both translational position and velocity signals simultaneously, and that hand position has a shifting effect on the velocity tuning curve, indicating an additive relationship between translational position and velocity (Wang et al., 2007). We took a similar approach to visualize the effect of hand rotation on translational direction tuning curve for neurons representing nonlinear interaction between hand translation and rotation. For each neuron, a hand translation tuning curve for each rotation condition was built by plotting the average firing rate against translation direction (Fig. 3A). Neuronal activities for all neurons representing nonlinear interaction between hand translation and rotation were normalized by their root-mean-square values and averaged together to generate a population average. As can be seen in Figure 3B, there is clearly a multiplicative relationship between cortical representations of hand translation and rotation.

Figure 3.

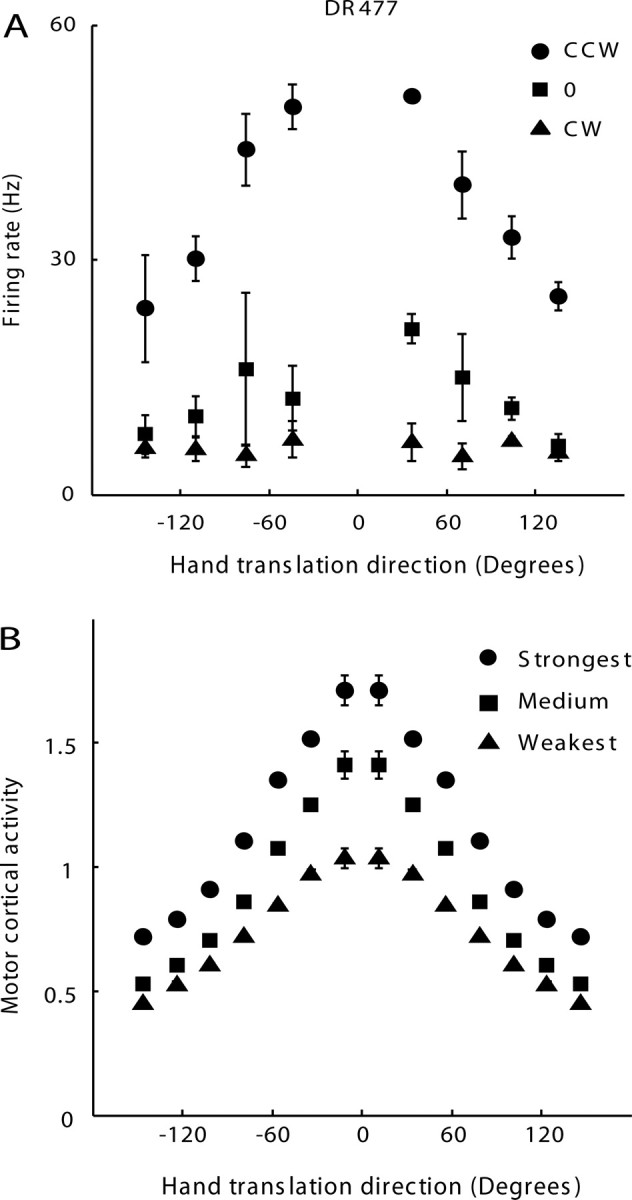
Figure 3.

Open in a new tab

Neuronal encoding of both translation and rotation in a gain field manner. A, For each rotation direction, firing rate of a representative M1 neuron was plotted as a function of translation direction, with 0° indicating the PD. Firing rates corresponding to different rotation directions are marked with different symbols, and error bars indicate SEs. For CCW rotation, the neuron achieved maximum firing rate when the hand was translating along its PD, agreeing with the cosine tuning model. For CW rotation, there was no difference in firing rate across different translation directions. This suggests that this M1 neuron encodes both translation and rotation in a multiplicative, or gain field, manner. B, Generalized tuning curves were made by normalizing the firing rate data of individual neurons and averaging across all 131 neurons modulated by nonlinear interaction between translation and rotation. Round dots, squares, and triangles correspond to rotation conditions with the strongest, medium, and the weakest neuronal responses, respectively. Data points represented by the same symbols make up a cosine tuning curve for hand translation. Data from 0° to 180° were mirrored to −180° to 0° for visualization purpose. Similar to single neuron responses, the cosine tuning curves were modulated by a gain field encoding hand rotation.

Cosine tuning curves for each rotation direction were fit to neuronal activities in Figure 3B. The depths of modulation (i.e., amplitude of the cosine tuning curves) and their 95% confidence intervals (CIs) were as follows: 0.53 ± 0.03, 0.45 ± 0.02, and 0.32 ± 0.01. The 95% CIs did not overlap with each other, indicating that the depths of modulation of those three cosine tuning curves were significantly different (p < 0.05), confirming the multiplicative relationship. Although only one rotational dimension was tested in this study, the data in Figure 3B suggest the following general motor cortical encoding model for 3D position, 3D translational velocity, 3D orientation, and 3D rotational velocity:

graphic file with name zns00310-7590-m02.jpg

where D is the total neural activity; b0,T is the average neural activity related to hand translation and b0,R is the average neural activity related to hand rotation; B⃗T is a 6 × 1 vector representing both the preferred direction and preferred positional gradient of the neuron; T⃗ is a 6 × 1 vector representing both the translational velocity and position of the hand in space (i.e., [ẋ, ẏ, ż, x, y, z]); B⃗R is a 6 × 1 vector representing both the preferred rotation and preferred orientation gradient of the neuron; and R⃗ is a 6 × 1 vector representing both the rotational velocity and orientation of the hand in space (i.e., [θ̇, ϕ̇, ψ̇, θ, ϕ, ψ]). Equation 1 is essentially a 12D model that encompasses the classic 3D cosine tuning model for translational movement first proposed by Georgopoulos et al. (1986). In their seminal work, Georgopoulos et al. (1986) were able to predict 3D movement direction from a population of active M1 neurons. A modified version of this algorithm, indirect OLE method, was used to predict hand kinematics (Wang et al., 2007). We were able to accurately predict the instantaneous hand translational and rotational velocities from a population of 512 movement-modulated motor cortical neurons during the center-out with rotation task (supplemental Figs. 6–8, available at www.jneurosci.org as supplemental material). Correlations between the actual and predicted values were 0.86, 0.83, 0.91, and 0.69 for the forward, upward, rightward, and roll velocities, respectively.

Discussion

This study has three major findings. First, there are a substantial number of motor cortical neurons encoding both hand translation and hand rotation. Second, the temporal characteristics of the neuronal firing rates indicate that hand rotational velocity is more strongly represented than hand orientation. Third and most important, motor cortical representations of translation and rotation interact with each other in a multiplicative manner. Classical psychophysical studies on visually guided reaching and grasping movement suggest that there are two separate and parallel processing streams, one for hand translation, and one for rotating and preshaping the hand to grasp the target (Arbib et al., 1985). Neurophysiological studies in visual pathways have found evidence supporting the idea of two separate processing streams. For example, the dorsal (parietal) stream processes the position of an object, and the ventral (inferotemporal) stream processes the orientation and shape of an object (DeYoe and Van Essen, 1988). The dorsal stream can be further divided into dorsal-dorsal stream and ventral-dorsal stream, subserving translational and rotational hand movement, respectively (Rizzolatti and Matelli, 2003). The existence of a common pool of motor cortical neurons representing both hand translation and rotation simultaneously indicates that those two parallel processing streams have converged by the time they arrive at M1. From an engineering perspective, convergence is logical since movement of the arm's musculoskeletal system is governed by a set of second-order differential equations where both translation and rotation are dynamically coupled; and, hence need to be coplanned. This study suggests motor cortex contains the appropriate state variable information (i.e., arm kinematics) to appropriately plan tightly coupled translational and rotational movements of the hand during daily activities. Furthermore, this study has direct clinical application for neuroprosthetics. Being able to simultaneously decode desired hand position and orientation from a population of motor cortical neurons could allow paralyzed individuals to control robotic arms to accurately transport and rotate objects during activities of daily living, such as drinking a cup of water or opening a door by turning the handle.

Footnotes

This work was supported by the Whitaker Foundation and was performed in a facility supported by National Center for Research Resources Grant C06RR-015502. We thank H. Hobbs for assisting in the experiments.

References

  1. Arbib MA, Iberall T, Lyons D. Coordinated control programs for movements of the hand. Exp Brain Res [Suppl] 1985;10:111–129. [Google Scholar]
  2. Ashe J, Georgopoulos AP. Movement parameters and neural activity in motor cortex and area 5. Cereb Cortex. 1994;4:590–600. doi: 10.1093/cercor/4.6.590. [DOI] [PubMed] [Google Scholar]
  3. Baker SN, Philbin N, Spinks R, Pinches EM, Wolpert DM, MacManus DG, Pauluis Q, Lemon RN. Multiple single unit recording in the cortex of monkeys using independently moveable microelectrodes. J Neurosci Methods. 1999;94:5–17. doi: 10.1016/s0165-0270(99)00121-1. [DOI] [PubMed] [Google Scholar]
  4. Bernstein N. The problem of the interrelation of coordination and localization. Arch Biol Sci. 1935;38:1–35. [Google Scholar]
  5. DeYoe EA, Van Essen DC. Concurrent processing streams in monkey visual cortex. Trends Neurosci. 1988;11:219–226. doi: 10.1016/0166-2236(88)90130-0. [DOI] [PubMed] [Google Scholar]
  6. Fu QG, Flament D, Coltz JD, Ebner TJ. Temporal encoding of movement kinematics in the discharge of primate primary motor and premotor neurons. J Neurophysiol. 1995;73:836–854. doi: 10.1152/jn.1995.73.2.836. [DOI] [PubMed] [Google Scholar]
  7. Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J Neurosci. 1982;2:1527–1537. doi: 10.1523/JNEUROSCI.02-11-01527.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Georgopoulos AP, Schwartz AB, Kettner RE. Neuronal population coding of movement direction. Science. 1986;233:1416–1419. doi: 10.1126/science.3749885. [DOI] [PubMed] [Google Scholar]
  9. Kakei S, Hoffman DS, Strick PL. Muscle and movement representations in the primary motor cortex. Science. 1999;285:2136–2139. doi: 10.1126/science.285.5436.2136. [DOI] [PubMed] [Google Scholar]
  10. Kettner RE, Schwartz AB, Georgopoulos AP. Primate motor cortex and free arm movements to visual targets in three-dimensional space. III. Positional gradients and population coding of movement direction from various movement origins. J Neurosci. 1988;8:2938–2947. doi: 10.1523/JNEUROSCI.08-08-02938.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Moran DW, Schwartz AB. Motor cortical representation of speed and direction during reaching. J Neurophysiol. 1999;82:2676–2692. doi: 10.1152/jn.1999.82.5.2676. [DOI] [PubMed] [Google Scholar]
  12. Paninski L, Fellows MR, Hatsopoulos NG, Donoghue JP. Spatiotemporal tuning of motor cortical neurons for hand position and velocity. J Neurophysiol. 2004;91:515–532. doi: 10.1152/jn.00587.2002. [DOI] [PubMed] [Google Scholar]
  13. Reina GA, Moran DW, Schwartz AB. On the relationship between joint angular velocity and motor cortical discharge during reaching. J Neurophysiol. 2001;85:2576–2589. doi: 10.1152/jn.2001.85.6.2576. [DOI] [PubMed] [Google Scholar]
  14. Richmond BJ, Optican LM, Podell M, Spitzer H. Temporal encoding of two-dimensional patterns by single units in primate inferior temporal cortex. I. Response characteristics. J Neurophysiol. 1987;57:132–146. doi: 10.1152/jn.1987.57.1.132. [DOI] [PubMed] [Google Scholar]
  15. Rizzolatti G, Matelli M. Two different streams form the dorsal visual system: anatomy and functions. Exp Brain Res. 2003;153:146–157. doi: 10.1007/s00221-003-1588-0. [DOI] [PubMed] [Google Scholar]
  16. Schwartz AB, Kettner RE, Georgopoulos AP. Primate motor cortex and free arm movements to visual targets in three-dimensional space. I. Relations between single cell discharge and direction of movement. J Neurosci. 1988;8:2913–2927. doi: 10.1523/JNEUROSCI.08-08-02913.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Wang W, Chan SS, Heldman DA, Moran DW. Motor cortical representation of position and velocity during reaching. J Neurophysiol. 2007;97:4258–4270. doi: 10.1152/jn.01180.2006. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES