Figure 2.

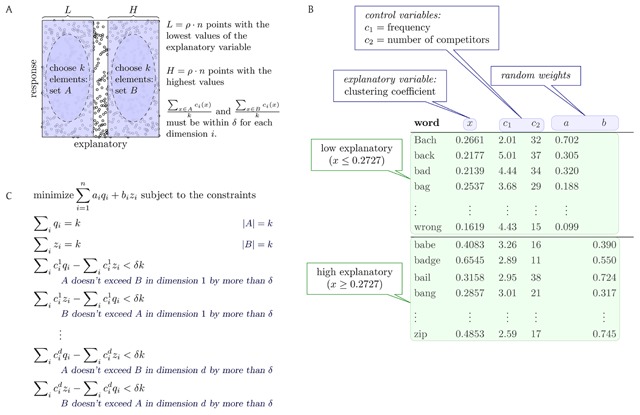
A schematic of the selection process, with parameters k (size of chosen subsets), ρ (fraction of data considered “high” or “low”), and δ (tolerance in control variables). (A) We must choose 2k of n given data points, in two equal-sized sets A and B, where A is chosen from among the ρ · n points with lowest explanatory variable values and B is chosen from among the ρ · n highest points. In every control dimension c_i, the elements of A and B are, on average, within δ. (B) A particular example of this input data in a SWR context, with data from the ELP lexicon (Balota et al., 2007; Brysbaert & New, 2009). The weights a_i and b_i are chosen uniformly at random from [0,1]. The desired solution is the lightest-weight pair of sets A and B (with respect to these particular a and b weights) that satisfies the control-dimension constraints. (C) The integer linear program (ILP) used to compute the solution. We define variables q_i ∈ {0, 1} and z_i ∈ {0, 1} indicating whether to include a point in A and B, respectively. Solving the ILP finds optimal values of q_i and z_i. Fresh random weights are chosen in each run of the algorithm.