Figure 4.

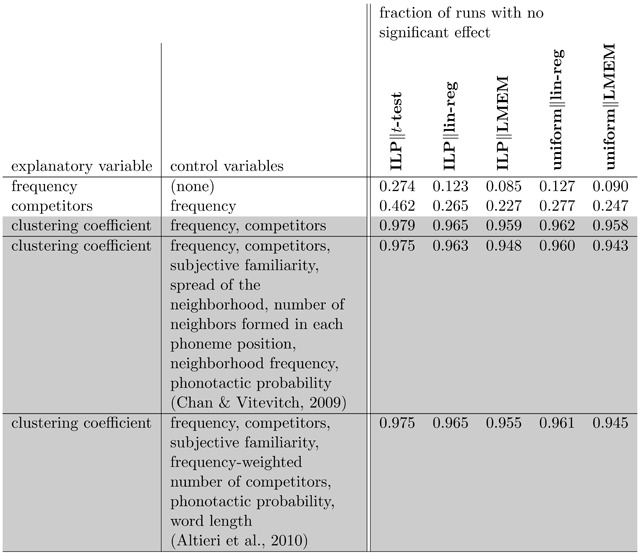
Comparison of power of various testing methodologies. We considered two explanatory variables with significant effect on recognition accuracy in SWR1081, as determined by linear regression and LMEM applied to the entire dataset (p < 0.001 for both frequency and competitors). We measured how often five different testing methodologies failed to detect the correct effect (at the p = 0.05 level) in subpopulations of 100 total words, over 5000 trials. ILP selection follows Figure 2; uniform selection chooses the same number of elements by uniform random sampling. We tested for a relationship using either a t-test comparing the low and high sets’ response-variable values, via linear regression (in either case controlling for the listed control variables), or LMEM. The first two rows show settings in which there is a true effect (measured on the whole dataset); here, linear regression and LMEM correctly detect an effect more frequently than t-tests. When used with linear regression or LMEM, ILP performed slightly better than uniform sampling. For contrast, the last three rows show a setting in which there is no apparent relationship on the whole dataset (p > 0.5 using both linear regression and LMEM), where all three methodologies showed no effect >94% of the time. The last two of these rows perform the clustering coefficient analysis while controlling for a much larger list of variables, following the methodology of Chan and Vitevitch (2009) and Altieri et al. (2010). Note that we did not directly attempt to correct for multicollinearity among variables; however, given the close similarity of the analyses in the last three rows of the table, which correspond to very different settings of control variables, and the fact that all of the ILP analyses (which control for covariates via selection rather than only statistically) are consistent with the uniform analyses, multicollinearity is not likely to substantially affect the results.