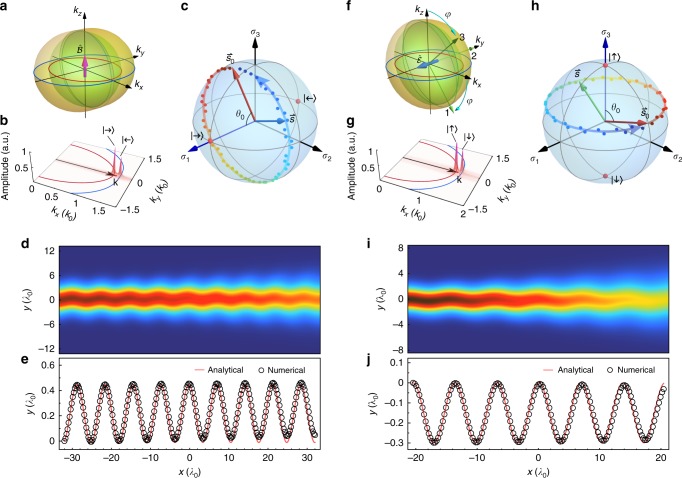
Fig. 1.

Zitterbewegung effect in homogeneous non-Abelian media. a–e ZB induced by a synthetic non-Abelian magnetic field in a gyrotropic medium with the parameters ${\mathrm{\leftrightarrow \epsilon }}_T={\mathrm{\leftrightarrow \mu }}_T=1.5{\overleftrightarrow{\mathbf{I}}}_{2\times 2}$, ${\epsilon }_z={\mu }_z=1.5$, ${\mathbf{g}}_1=-{\mathbf{g}}_2^{*}={\left(0.3\mathrm{i},-0.07\right)}^{\top }$. This medium produces a synthetic SU(2) magnetic field along $z$ direction, $\widehat{\mathcal{B}}=-k_0^{2}0.042{\mathbf{e}}_z{\widehat{\sigma }}_3$, with a null SU(2) electric field $\widehat{\mathcal{E}}=0$. f–j ZB induced by a synthetic non-Abelian electric field in a biaxial non-magnetic medium with the parameters ${\epsilon }_1=1.65$, ${\epsilon }_2=2.45$, ${\epsilon }_3=3$, and $\mu ∕{\mu }_0=1$. The synthetic $\mathrm{SU}\left(2\right)$ electric field, $\widehat{\mathcal{E}}=-k_0^{3}0.08919{\mathbf{e}}_y{\widehat{\sigma }}_2$, is along the y-aixs, while the SU(2) magnetic field vanishes $\widehat{\mathcal{B}}=0$. a, f The isofrequency surfaces and their xy cross sections (red and blue curves) of both cases. The green arrows in f are the three principal axes 1, 2, 3 of permittivity tensor. b, g Fourier spectra in k-space of the beams in the two media. In each case, the two peaks in the spectrum correspond to the two eigenmodes with wave vectors in the x direction. And the average wave vectors k are marked by the black arrows. c, h The spin precession along each beam on the Bloch sphere. The colored dots are the numerical data within one ZB period. d, i Full-wave simulated intensity distributions, where the beam waists equal $4.4{\lambda }_0$ and $6.2{\lambda }_0$, respectively (${\lambda }_0=2\pi ∕k_0$ is the wavelength in vacuum). e, j Numerical (black circles) and analytical (red curves) trajectories of the intensity centroid