Fig. 3.

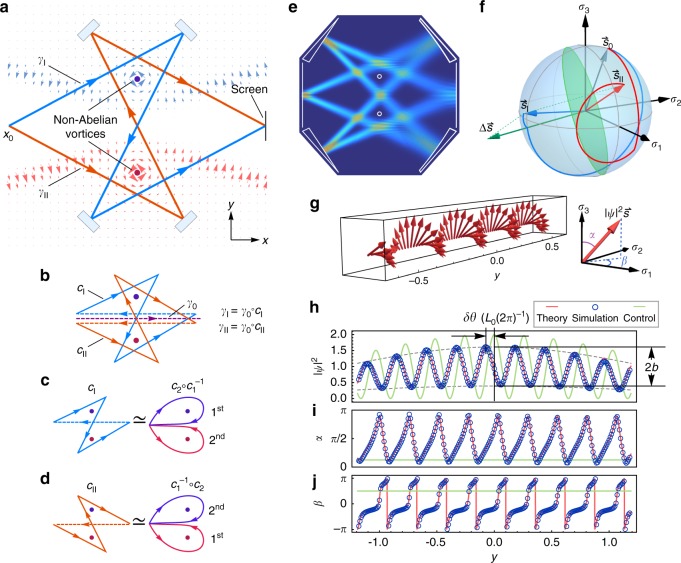
Genuine non-Abelian AB effect for light. a Sketch of the non-Abelian AB system with two optical paths ${\gamma }_{\mathrm{I}}$, ${\gamma }_{\mathrm{II}}$ interfering on the screen, where the background light blue (red) arrows denote the ${\widehat{\sigma }}_1$ (${\widehat{\sigma }}_2$) component ${\mathcal{A}}^1$ $\left({\mathcal{A}}^2\right)$ of the non-Abelian vector potential. b ${\gamma }_{\mathrm{I}}$ (${\gamma }_{\mathrm{II}}$) can be divided into a closed loop $c_{\mathrm{I}}$ ($c_{\mathrm{II}}$) and a common path γ₀. c, d c_I and c_II can, respectively, deform continuously into a closed path that winds around the two vortices successively but in opposite sequences. e Snapshot of the simulated field intensity for the proposed non-Abelian optical interferometer with incident spinor ${\left(1,\mathrm{i}1∕5\right)}^{\top }$ for both beams and the vortex fluxes ${\mathrm{\Phi }}_1=-2\pi ∕3$, ${\mathrm{\Phi }}_2=-\pi ∕3$. f Spin evolution on the Bloch sphere along two beams ${\gamma }_{\mathrm{I}}$, ${\gamma }_{\mathrm{II}}$, which share the same initial spin ${\overrightarrow{s}}_0$ but achieve different final spins ${\overrightarrow{s}}_{\mathrm{I}}$ and ${\overrightarrow{s}}_{\mathrm{II}}$. g Spin density interference corresponding to e, where each arrow denotes the local pseudo-spin density $\mid \psi {\mid }^2\overrightarrow{s}$ at a point on the screen. All of the local spins $\overrightarrow{s}\left(y\right)$ are perpendicular to $\Delta \overrightarrow{s}={\overrightarrow{s}}_{\mathrm{I}}-{\overrightarrow{s}}_{\mathrm{II}}$, and thus fall on the green circle in f. The corresponding intensity interference $\mid \psi {\mid }^2\left(y\right)$ and the two Euler angles α, β of the local spins $\overrightarrow{s}\left(y\right)$ on the screen are shown in h–j, where blue circles and red curves indicate simulated and theoretical results, respectively, and $\delta \theta$, b are the phase shift and relative amplitude relative to the case of $\widehat{\mathcal{A}}=0$ (L₀ is the period of $\Delta \theta \left(y\right)\mathrm{mod}2\pi$). The green lines correspond to the “control experiment”